Word ladder II
Graphs
Hard Problems
Hard
- This type of problem is central in applications such as machine translation, autocorrect algorithms, or even text-based games
- The ability to transform one word into another by changing letters, while still producing valid words, forms the foundation of such systems
- The concept is known as Levenshtein distance or Edit distance in computer science, which measures the minimum number of operations (transformations) required to change one word into another
- It is a popular algorithm in Natural Language Processing and Computational Linguistics
Given two distinct words startWord and targetWord, and a list denoting wordList of unique words of equal lengths. Find all shortest transformation sequence(s) from startWord to targetWord. You can return them in any order possible.
In this problem statement, we need to keep the following conditions in mind:
A word can only consist of lowercase characters.
Only one letter can be changed in each transformation.
Each transformed word must exist in the wordList including the targetWord.
startWord may or may not be part of the wordList.
Return an empty list if there is no such transformation sequence.
Examples:
Input: startWord = "der", targetWord = "dfs", wordList = ["des", "der", "dfr", "dgt", "dfs"]
Output: [ [ “der”, “dfr”, “dfs” ], [ “der”, “des”, “dfs”] ]
Explanation: The length of the smallest transformation sequence here is 3.
Following are the only two shortest ways to get to the targetWord from the startWord :
"der" -> ( replace ‘r’ by ‘s’ ) -> "des" -> ( replace ‘e’ by ‘f’ ) -> "dfs".
"der" -> ( replace ‘e’ by ‘f’ ) -> "dfr" -> ( replace ‘r’ by ‘s’ ) -> "dfs".
Input: startWord = "gedk", targetWord= "geek", wordList = ["geek", "gefk"]
Output: [ [ “gedk”, “geek” ] ]
Explanation: The length of the smallest transformation sequence here is 2.
Following is the only shortest way to get to the targetWord from the startWord :
"gedk" -> ( replace ‘d’ by ‘e’ ) -> "geek".
Input: startWord = "abc", targetWord = "xyz", wordList = ["abc", "ayc", "ayz", "xyz"]
Constraints
- N= Number of Words
- M= Length of Word
- 1 ≤ N ≤ 100
- 1 ≤ M ≤ 10
Hints
- "Bidirectional BFS is optimal, reducing the search space by simultaneously expanding from startWord and targetWord until they meet in the middle. Instead of storing only distances, we store parent mappings to track how each word was reached, allowing us to reconstruct all shortest paths efficiently."
- "After finding the shortest path depth using BFS, we use Depth-First Search (DFS) or backtracking to reconstruct all possible sequences. The parent mapping stores how each word was reached during BFS, and DFS reconstructs sequences by following this mapping back from targetWord to startWord."
Company Tags
MongoDB
eBay
Instacart
McKinsey & Company
Oracle
Twilio
JPMorgan Chase
Nutanix
American Express
Bain & Company
Seagate Technology
Ubisoft
Airbnb
Broadcom
Robinhood
Bloomberg
PayPal
NVIDIA
Salesforce
Databricks
Cloudflare
Zynga
Ernst & Young
Etsy
Mastercard
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Pre Requisite: Word Ladder I
Intuition:
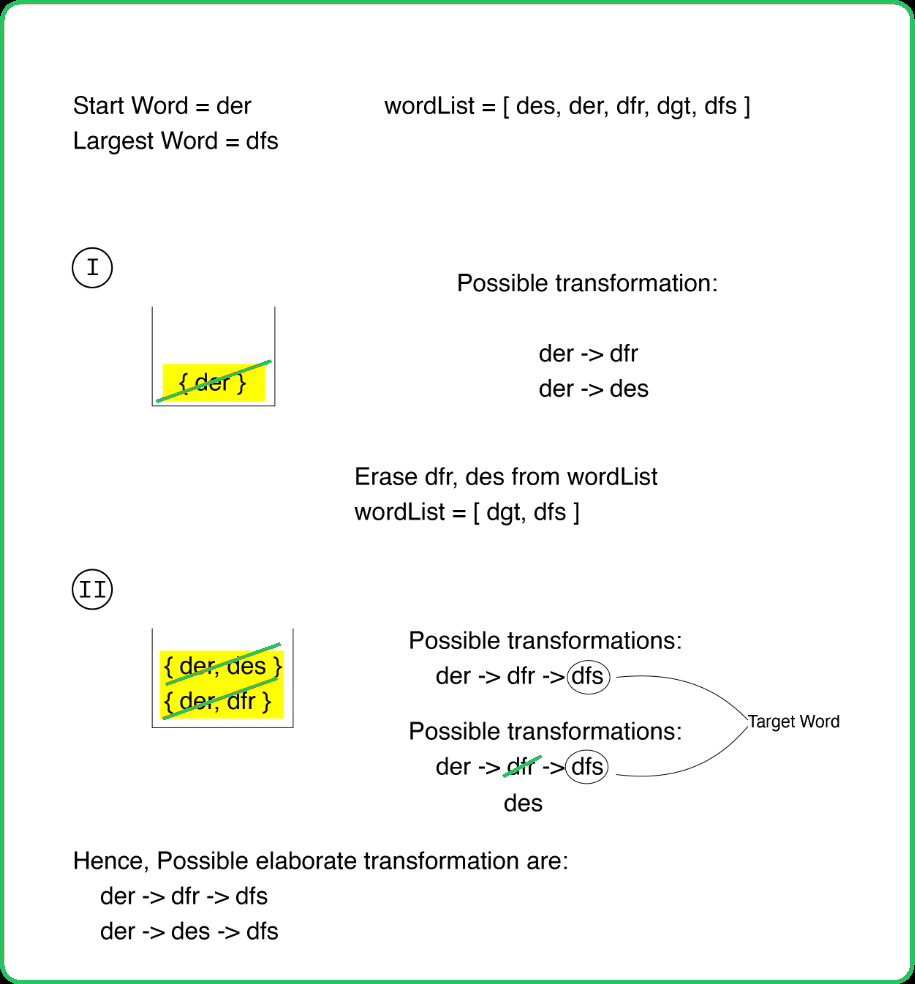
In this problem, all the possible transformations from the startWord to endWord must be found. Hence, in contrary to the previous problem, we do not stop the traversal on the first occurrence of endWord,but rather continue it for as many occurrences of the word as possible as we need all the shortest possible sequences in order to reach the end word.
Modification:
In the previous solution, whenever a word was matched from the given wordList, it was immediately erased from the Hashmap to avoid visiting it via a longer path. But since, here all the possible transformations must be returned, erasing it from the Hashmap might lose some of the possible transformations leading through it.Thus, instead of erasing the word immediately when it is found, the erase/delete operation can be performed after the traversal for all the words for a particular level is completed allowing exploration of all the paths.
Understanding:
In order to form the different sequences for transformations in a particular level, the concept of Backtracking can be used.- After adding the new word to a sequence, it is immediately removed (backtracked) to restore the sequence to its original state after the sequence is added to the queue.
- This backtracking step ensures that the original sequence can be used to try other possible transformations at the current level of the BFS.
Approach:
- Use a queue for breadth-first search (BFS) to handle sequences of word transformations. Add all words from the word list to a set for quick lookup. Start with the initial word and add it to the queue.
- Perform BFS level by level. For each word in the current level:
- Check if it matches the target word and add the sequence to the results. Generate all possible single-letter transformations.
- If a transformed word exists in the set, add it to the current sequence and push the sequence into the queue for further exploration.
- Mark words to be removed after the current level to prevent revisiting.
- After adding a transformed word to the sequence, immediately remove it to restore the sequence for the next transformation.
- Remove words marked during the level traversal from the set to prevent revisiting. Exit early if any sequences reaching the target word are found.
- Return the list of resulting sequences.
Dry Run:
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to determine number of steps
to reach from start ward to target word */
vector<vector<string>> findSequences(string beginWord, string endWord,
vector<string> &wordList) {
// To store the answer
vector<vector<string>> ans;
/* Queue data structure to store
the sequence of transformations */
queue <vector<string>> q;
// Add all the words to a hashset
unordered_set<string> st(wordList.begin(),
wordList.end());
// Add the sequence containing starting word to queue
q.push({beginWord});
// Erase starting word from set if it exists
st.erase(beginWord);
/* Set to store the words that must be deleted
after traversal of a level is complete */
unordered_set <string> toErase;
// Until the queue is empty
while(!q.empty()) {
// Size of queue
int size = q.size();
// Traversing all words in current level
for(int i=0; i<size; i++) {
// Sequence
vector<string> seq = q.front();
// Last added word in sequence
string word = seq.back();
q.pop();
// If the Last word same as end word
if(word == endWord) {
// Add the sequence to the answer
if(ans.empty()) {
ans.push_back(seq);
}
else if(ans.back().size() == seq.size()) {
ans.push_back(seq);
}
}
// Iterate on every character
for(int pos = 0; pos < word.length(); pos++){
// Original letter
char original = word[pos];
/* Replacing current character with
letters from 'a' to 'z' to match
any possible word from set */
for(char ch = 'a'; ch <= 'z'; ch++) {
word[pos] = ch;
// Check if it exists in the set
if(st.find(word) != st.end()) {
// Update the sequence
seq.push_back(word);
// Push in the queue
q.push(seq);
// Add the word to erase map
toErase.insert(word);
// Backtracking step
seq.pop_back();
}
}
// Update the original letter back
word[pos] = original;
}
}
/* Erase all the words in set after
traversal of a level is completed */
for(auto it : toErase) st.erase(it);
toErase.clear();
// If answer is found, break
if(!ans.empty()) break;
}
// Return the result found
return ans;
}
};
int main() {
string beginWord = "der", endWord = "dfs";
vector<string> wordList =
{"des","der","dfr","dgt","dfs"};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to determine number of
steps to reach from start ward to target word */
vector<vector<string>> ans =
sol.findSequences(beginWord, endWord, wordList);
// Output
cout << "The different sequences are:\n";
for(int i=0; i < ans.size(); i++) {
for(int j=0; j < ans[i].size(); j++) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
import java.util.*;
class Solution {
/* Function to determine number of steps
to reach from start word to target word */
public List<List<String>> findSequences(String beginWord, String endWord,
List<String> wordList) {
// To store the answer
List<List<String>> ans = new ArrayList<>();
// Queue data structure to store
// the sequence of transformations
Queue<List<String>> q = new LinkedList<>();
// Add all the words to a hashset
Set<String> st = new HashSet<>(wordList);
// Add the sequence containing starting word to queue
q.add(new ArrayList<>(Arrays.asList(beginWord)));
// Erase starting word from set if it exists
st.remove(beginWord);
// Set to store the words that must be deleted
// after traversal of a level is complete
Set<String> toErase = new HashSet<>();
// Until the queue is empty
while (!q.isEmpty()) {
// Size of queue
int size = q.size();
// Traversing all words in current level
for (int i = 0; i < size; i++) {
// Sequence
List<String> seq = q.poll();
// Last added word in sequence
String word = seq.get(seq.size() - 1);
// If the last word same as end word
if (word.equals(endWord)) {
// Add the sequence to the answer
if (ans.isEmpty()) {
ans.add(new ArrayList<>(seq));
}
else if (ans.get(ans.size() - 1).size() ==
seq.size()) {
ans.add(new ArrayList<>(seq));
}
}
// Iterate on every character
for (int pos = 0; pos < word.length(); pos++) {
// Original letter
char original = word.charAt(pos);
// Replacing current character with
// letters from 'a' to 'z' to match
// any possible word from set
for (char ch = 'a'; ch <= 'z'; ch++) {
char[] wordArray = word.toCharArray();
wordArray[pos] = ch;
String newWord = new String(wordArray);
// Check if it exists in the set
if (st.contains(newWord)) {
// Update the sequence
seq.add(newWord);
// Push in the queue
q.add(new ArrayList<>(seq));
// Add the word to erase map
toErase.add(newWord);
// Backtracking step
seq.remove(seq.size() - 1);
}
}
// Update the original letter back
String beforePos = word.substring(0, pos);
String afterPos = word.substring(pos + 1);
word = beforePos + original + afterPos;
}
}
// Erase all the words in set after
// traversal of a level is completed
for (String it : toErase) st.remove(it);
toErase.clear();
// If answer is found, break
if (!ans.isEmpty()) break;
}
// Return the result found
return ans;
}
public static void main(String[] args) {
String beginWord = "der", endWord = "dfs";
List<String> wordList = new ArrayList<>(Arrays.asList("des", "der", "dfr", "dgt", "dfs"));
// Creating an instance of
// Solution class
Solution sol = new Solution();
// Function call to determine number of
// steps to reach from start word to target word
List<List<String>> ans = sol.findSequences(beginWord, endWord, wordList);
// Output
System.out.println("The different sequences are:");
for (List<String> sequence : ans) {
for (String word : sequence) {
System.out.print(word + " ");
}
System.out.println();
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111
from collections import deque
class Solution:
# Function to determine number of steps
# to reach from start word to target word
def findSequences(self, beginWord, endWord, wordList):
# To store the answer
ans = []
# Queue data structure to store
# the sequence of transformations
q = deque()
# Add all the words to a hashset
st = set(wordList)
# Add the sequence containing starting word to queue
q.append([beginWord])
# Erase starting word from set if it exists
st.discard(beginWord)
# Set to store the words that must be deleted
# after traversal of a level is complete
toErase = set()
# Until the queue is empty
while q:
# Size of queue
size = len(q)
# Traversing all words in current level
for _ in range(size):
# Sequence
seq = q.popleft()
# Last added word in sequence
word = seq[-1]
# If the last word same as end word
if word == endWord:
# Add the sequence to the answer
if not ans:
ans.append(seq)
elif len(ans[-1]) == len(seq):
ans.append(seq)
# Iterate on every character
for pos in range(len(word)):
# Original letter
original = word[pos]
# Replacing current character with
# letters from 'a' to 'z' to match
# any possible word from set
for ch in 'abcdefghijklmnopqrstuvwxyz':
word = word[:pos] + ch + word[pos + 1:]
# Check if it exists in the set
if word in st:
# Update the sequence
seq.append(word)
# Push in the queue
q.append(list(seq))
# Add the word to erase map
toErase.add(word)
# Backtracking step
seq.pop()
# Update the original letter back
word = word[:pos] + original + word[pos + 1:]
# Erase all the words in set after
# traversal of a level is completed
for it in toErase:
st.discard(it)
toErase.clear()
# If answer is found, break
if ans:
break
# Return the result found
return ans
if __name__ == "__main__":
beginWord = "der"
endWord = "dfs"
wordList = ["des", "der", "dfr", "dgt", "dfs"]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to determine number of
# steps to reach from start word to target word
ans = sol.findSequences(beginWord, endWord, wordList)
# Output
print("The different sequences are:")
for sequence in ans:
print(" ".join(sequence))
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126
class Solution {
/* Function to determine number of steps
to reach from start word to target word */
findSequences(beginWord, endWord, wordList) {
// To store the answer
const ans = [];
// Queue data structure to store
// the sequence of transformations
const q = [];
// Add all the words to a hashset
const st = new Set(wordList);
// Add the sequence containing starting word to queue
q.push([beginWord]);
// Erase starting word from set if it exists
st.delete(beginWord);
// Set to store the words that must be deleted
// after traversal of a level is complete
const toErase = new Set();
// Until the queue is empty
while (q.length > 0) {
// Size of queue
const size = q.length;
// Traversing all words in current level
for (let i = 0; i < size; i++) {
// Sequence
const seq = q.shift();
// Last added word in sequence
let word = seq[seq.length - 1];
// If the last word same as end word
if (word === endWord) {
// Add the sequence to the answer
if (ans.length === 0) {
ans.push([...seq]);
}
else if (ans[ans.length - 1].length ===
seq.length) {
ans.push([...seq]);
}
}
// Iterate on every character
for (let pos = 0; pos < word.length; pos++) {
// Original letter
const original = word[pos];
// Replacing current character with
// letters from 'a' to 'z' to match
// any possible word from set
for (let ch = 97; ch <= 122; ch++) {
word = word.slice(0, pos) +
String.fromCharCode(ch) +
word.slice(pos + 1);
// Check if it exists in the set
if (st.has(word)) {
// Update the sequence
seq.push(word);
// Push in the queue
q.push([...seq]);
// Add the word to erase map
toErase.add(word);
// Backtracking step
seq.pop();
}
}
// Update the original letter back
word = word.slice(0, pos) +
original +
word.slice(pos + 1);
}
}
// Erase all the words in set after
// traversal of a level is completed
for (const it of toErase) st.delete(it);
toErase.clear();
// If answer is found, break
if (ans.length > 0) break;
}
// Return the result found
return ans;
}
}
const main = () => {
const beginWord = "der";
const endWord = "dfs";
const wordList = ["des", "der", "dfr", "dgt", "dfs"];
// Creating an instance of
// Solution class
const sol = new Solution();
// Function call to determine number of
// steps to reach from start word to target word
const ans = sol.findSequences(beginWord, endWord, wordList);
// Output
console.log("The different sequences are:");
for (const sequence of ans) {
console.log(sequence.join(" "));
}
};
main();
Complexity Analysis:
Time Complexity: O(N*M*26)
- In the worst case, the steps required to reach from startWord to targetWord can go up to N. During each step, all the characters for the word are replaced from 'a' to 'z' taking O(M*26) time.
- Adding all the words in wordList takes O(N) time.
- Each word is enqueued and dequeued at most once, leading to O(N) queue operations.
- Checking if a word exists in the set and removing a word from the set takes O(1) on average. If there are N words, there are O(N) set operations.
Space Complexity: O(N*M)
A HashSet is used to store words in wordList taking O(N) space. In the worst case, the queue will store all possible sequences leading to a space requirement of O(N*M). Storing the result in a list will take O(N*M) space.
Intuition:
A more efficient way to find all the shortest possible transformations from the Start Word to End Word is by using a combination of BFS traversal for level-order traversal and DFS for backtracking.
Understanding:
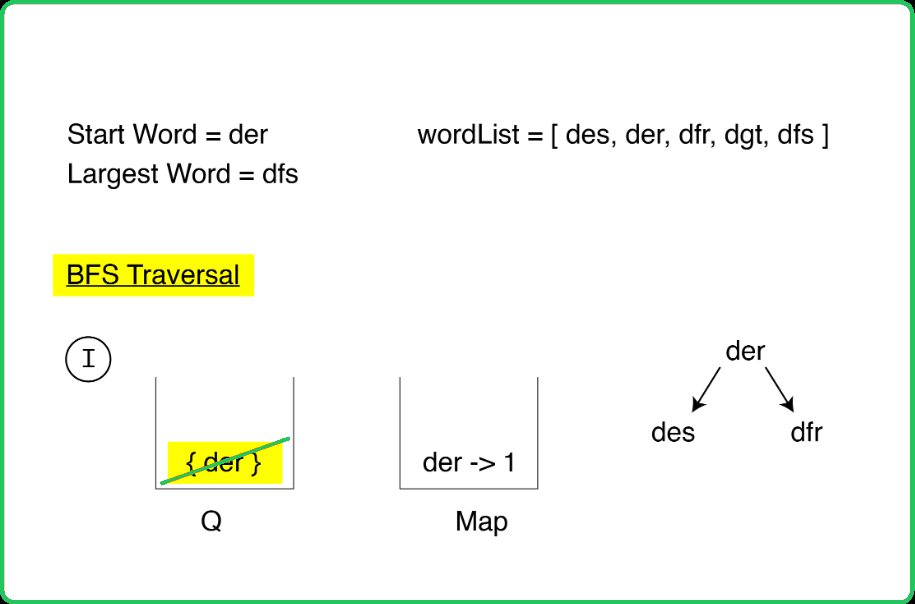
- Breadth-First Search (BFS): BFS is used to find the shortest path from beginWord to endWord. BFS explores all words level by level, ensuring that the shortest path is found first. The re-processing of nodes can be avoided by using a map to track the shortest distance to each word.
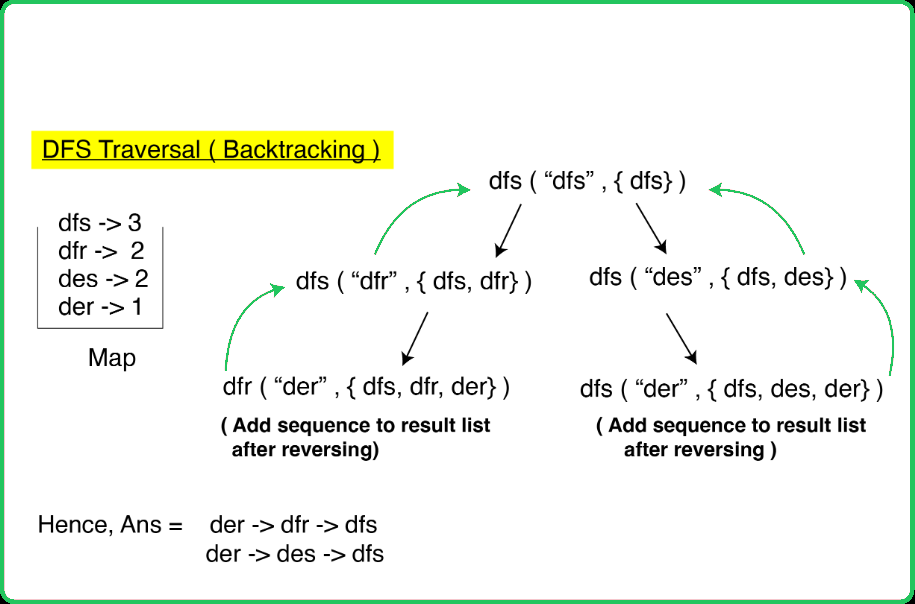
- Depth-First Search (DFS): After the BFS completes, DFS can be used to backtrack from endWord to beginWord. DFS helps to reconstruct all the shortest paths found by BFS.
Edge Cases:
If it not possible to reach the target word from the start word, the Backtracking step can be skipped and an empty list can be returned as the answer.
Approach:
- Create a set containing all words from the provided word list and a queue to facilitate BFS traversal. Additionally, use a map to keep track of the minimum steps needed to reach each word from the start word.
- Start from the initial word and perform BFS. For each word, explore all possible transformations by changing each character to every letter from 'a' to 'z'.
- If a transformed word is found in the word list set, it is added to the queue and the map with incremented steps. The word is then removed from the set to prevent revisiting.
- After BFS completes, check if the target word is present in the map. If not, return an empty list as there is no transformation sequence.
- If the target word is found, use DFS to backtrack from the target word to the start word. The DFS reconstructs all shortest transformation sequences by following the steps stored in the map.
- Store the valid sequences found by DFS in a result list and return it.
Dry Run:
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function call to add the shortest
transformation using backtracking */
void dfs(string word, string &beginWord, vector<string> &seq,
unordered_map <string,int> &mpp, vector<vector<string>> &ans) {
// If the sequence is complete
if(word == beginWord) {
// Reverse the sequence
reverse(seq.begin(), seq.end());
// Store in the result
ans.push_back(seq);
// Reverse again for other possible sequences
reverse(seq.begin(), seq.end());
// Return
return;
}
// Steps to reach the word
int val = mpp[word];
// Try all possible transformations
for(int i=0; i < word.length(); i++) {
char original = word[i];
for(char ch = 'a'; ch <= 'z'; ch++) {
word[i] = ch;
// If a possible transformations is found
if(mpp.find(word) != mpp.end() &&
mpp[word] + 1 == val) {
// Update the sequence
seq.push_back(word);
// Make recursive DFS call
dfs(word, beginWord, seq, mpp, ans);
// Pop back for backtracking
seq.pop_back();
}
}
word[i] = original;
}
}
public:
/* Function to determine number of steps
to reach from start ward to target word */
vector<vector<string>> findSequences(string beginWord, string endWord,
vector<string>& wordList) {
// Length of words
int len = beginWord.length();
// Add all the words to a hashset
unordered_set <string> st(wordList.begin(),
wordList.end());
/* Hash map to store the minimum
steps needed to reach a word */
unordered_map <string,int> mpp;
// Queue for BFS traversal
queue <string> q;
// Pushing intial word in the queue
q.push(beginWord);
/* Erasing the initial word from
the set if it exists */
st.erase(beginWord);
// Step count
int steps = 1;
// Storing the intial pair in map
mpp[beginWord] = steps;
// Until the queue is empty
while(!q.empty()) {
// Get the word and steps
string word = q.front();
steps = mpp[word];
q.pop();
// Check for every possible transformation
for(int i = 0; i < len; i++) {
char original = word[i];
for(char ch = 'a'; ch <= 'z'; ch++) {
word[i] = ch;
// If a possible transformation is found
if(st.find(word) != st.end()) {
// Store it in map
mpp[word] = steps+1;
// Push in the queue
q.push(word);
// Erase word from list
st.erase(word);
}
}
word[i] = original;
}
}
/* Return an empty list if reaching the
target word is not possible */
if(mpp.find(endWord) == mpp.end())
return {};
// To store the answer
vector<vector<string>> ans;
// To store the possible sequence of transformations
vector <string> seq = {endWord};
// Backtracking step
dfs(endWord, beginWord, seq, mpp, ans);
// Return the computed result
return ans;
}
};
int main() {
string beginWord = "der", endWord = "dfs";
vector<string> wordList =
{"des","der","dfr","dgt","dfs"};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to determine number of
steps to reach from start ward to target word */
vector<vector<string>> ans =
sol.findSequences(beginWord, endWord, wordList);
// Output
cout << "The different sequences are:\n";
for(int i=0; i < ans.size(); i++) {
for(int j=0; j < ans[i].size(); j++) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155
import java.util.*;
class Solution {
private void dfs(String word, String beginWord, List<String> seq,
Map<String, Integer> mpp, List<List<String>> ans) {
// If the sequence is complete
if (word.equals(beginWord)) {
// Reverse the sequence
Collections.reverse(seq);
// Store in the result
ans.add(new ArrayList<>(seq));
// Reverse again for other possible sequences
Collections.reverse(seq);
// Return
return;
}
// Steps to reach the word
int val = mpp.get(word);
// Try all possible transformations
for (int i = 0; i < word.length(); i++) {
char original = word.charAt(i);
StringBuilder sb = new StringBuilder(word);
for (char ch = 'a'; ch <= 'z'; ch++) {
sb.setCharAt(i, ch);
String newWord = sb.toString();
// If a possible transformation is found
if (mpp.containsKey(newWord) &&
mpp.get(newWord) + 1 == val) {
// Update the sequence
seq.add(newWord);
// Make recursive DFS call
dfs(newWord, beginWord, seq, mpp, ans);
// Pop back for backtracking
seq.remove(seq.size() - 1);
}
}
}
}
public List<List<String>> findSequences(String beginWord, String endWord,
List<String> wordList) {
// Length of words
int len = beginWord.length();
// Add all the words to a hashset
Set<String> st = new HashSet<>(wordList);
/* Hash map to store the minimum
steps needed to reach a word */
Map<String, Integer> mpp = new HashMap<>();
// Queue for BFS traversal
Queue<String> q = new LinkedList<>();
// Pushing initial word in the queue
q.add(beginWord);
// Erasing the initial word from the set if it exists
st.remove(beginWord);
// Step count
int steps = 1;
// Storing the initial pair in map
mpp.put(beginWord, steps);
// Until the queue is empty
while (!q.isEmpty()) {
// Get the word and steps
String word = q.poll();
steps = mpp.get(word);
// Check for every possible transformation
for (int i = 0; i < len; i++) {
char original = word.charAt(i);
StringBuilder sb = new StringBuilder(word);
for (char ch = 'a'; ch <= 'z'; ch++) {
sb.setCharAt(i, ch);
String newWord = sb.toString();
// If a possible transformation is found
if (st.contains(newWord)) {
// Store it in map
mpp.put(newWord, steps + 1);
// Push in the queue
q.add(newWord);
// Erase word from list
st.remove(newWord);
}
}
}
}
/* Return an empty list if reaching
the target word is not possible */
if (!mpp.containsKey(endWord))
return new ArrayList<>();
// To store the answer
List<List<String>> ans = new ArrayList<>();
// To store the possible sequence of transformations
List<String> seq = new ArrayList<>();
seq.add(endWord);
// Backtracking step
dfs(endWord, beginWord, seq, mpp, ans);
// Return the computed result
return ans;
}
public static void main(String[] args) {
String beginWord = "der", endWord = "dfs";
List<String> wordList = Arrays.asList(
"des", "der", "dfr", "dgt", "dfs"
);
// Creating an instance of Solution class
Solution sol = new Solution();
/* Function call to determine number of
steps to reach from start ward to target word */
List<List<String>> ans =
sol.findSequences(beginWord, endWord, wordList);
// Output
System.out.println("The different sequences are:");
for (List<String> seq : ans) {
for (String word : seq) {
System.out.print(word + " ");
}
System.out.println();
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133
from collections import deque
class Solution:
def dfs(self, word, beginWord, seq, mpp, ans):
# If the sequence is complete
if word == beginWord:
# Reverse the sequence
seq.reverse()
# Store in the result
ans.append(list(seq))
# Reverse again for other possible sequences
seq.reverse()
# Return
return
# Steps to reach the word
val = mpp[word]
# Try all possible transformations
for i in range(len(word)):
original = word[i]
for ch in range(ord('a'), ord('z') + 1):
transformed_word = word[:i] + chr(ch) + word[i + 1:]
# If a possible transformation is found
if (transformed_word in mpp and
mpp[transformed_word] + 1 == val):
# Update the sequence
seq.append(transformed_word)
# Make recursive DFS call
self.dfs(transformed_word, beginWord, seq, mpp, ans)
# Pop back for backtracking
seq.pop()
# Restore original word
word = word[:i] + original + word[i + 1:]
def findSequences(self, beginWord, endWord, wordList):
# Length of words
len_word = len(beginWord)
# Add all the words to a hashset
st = set(wordList)
# Hash map to store the minimum steps needed to reach a word
mpp = {}
# Queue for BFS traversal
q = deque([beginWord])
# Erasing the initial word from the set if it exists
if beginWord in st:
st.remove(beginWord)
# Step count
steps = 1
# Storing the initial pair in map
mpp[beginWord] = steps
# Until the queue is empty
while q:
# Get the word and steps
word = q.popleft()
steps = mpp[word]
# Check for every possible transformation
for i in range(len_word):
original = word[i]
for ch in range(ord('a'), ord('z') + 1):
transformed_word = word[:i] + chr(ch) + word[i + 1:]
# If a possible transformation is found
if transformed_word in st:
# Store it in map
mpp[transformed_word] = steps + 1
# Push in the queue
q.append(transformed_word)
# Erase word from list
st.remove(transformed_word)
# Restore original word
word = word[:i] + original + word[i + 1:]
# Return an empty list if reaching
# the target word is not possible
if endWord not in mpp:
return []
# To store the answer
ans = []
# To store the possible sequence of transformations
seq = [endWord]
# Backtracking step
self.dfs(endWord, beginWord, seq, mpp, ans)
# Return the computed result
return ans
if __name__ == "__main__":
beginWord = "der"
endWord = "dfs"
wordList = ["des", "der", "dfr", "dgt", "dfs"]
# Creating an instance of Solution class
sol = Solution()
# Function call to determine number of steps
# to reach from start word to target word
ans = sol.findSequences(beginWord, endWord, wordList)
# Output
print("The different sequences are:")
for seq in ans:
print(" ".join(seq))
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160
class Solution {
/* Function call to add the shortest
transformation using backtracking */
dfs(word, beginWord, seq, mpp, ans) {
// If the sequence is complete
if (word === beginWord) {
// Reverse the sequence
seq.reverse();
// Store in the result
ans.push([...seq]);
// Reverse again for other possible sequences
seq.reverse();
// Return
return;
}
// Steps to reach the word
const val = mpp.get(word);
// Try all possible transformations
for (let i = 0; i < word.length; i++) {
const original = word[i];
for (let chCode = 'a'.charCodeAt(0);
chCode <= 'z'.charCodeAt(0);
chCode++) {
const ch = String.fromCharCode(chCode);
const transformed_word = word.substring(0, i) + ch +
word.substring(i + 1);
// If a possible transformation is found
if (mpp.has(transformed_word) &&
mpp.get(transformed_word) + 1 === val) {
// Update the sequence
seq.push(transformed_word);
// Make recursive DFS call
this.dfs(transformed_word, beginWord, seq, mpp, ans);
// Pop back for backtracking
seq.pop();
}
}
word = word.substring(0, i) + original + word.substring(i + 1);
}
}
/* Function to determine number of steps
to reach from start word to target word */
findSequences(beginWord, endWord, wordList) {
// Length of words
const len = beginWord.length;
// Add all the words to a hashset
const st = new Set(wordList);
// Hash map to store the minimum steps needed to reach a word
const mpp = new Map();
// Queue for BFS traversal
const q = [];
// Pushing initial word in the queue
q.push(beginWord);
// Erasing the initial word from the set if it exists
st.delete(beginWord);
// Step count
let steps = 1;
// Storing the initial pair in map
mpp.set(beginWord, steps);
// Until the queue is empty
while (q.length) {
// Get the word and steps
let word = q.shift();
steps = mpp.get(word);
// Check for every possible transformation
for (let i = 0; i < len; i++) {
const original = word[i];
for (let chCode = 'a'.charCodeAt(0);
chCode <= 'z'.charCodeAt(0);
chCode++) {
const ch = String.fromCharCode(chCode);
const transformed_word = word.substring(0, i) +
ch +
word.substring(i + 1);
// If a possible transformation is found
if (st.has(transformed_word)) {
// Store it in map
mpp.set(transformed_word, steps + 1);
// Push in the queue
q.push(transformed_word);
// Erase word from list
st.delete(transformed_word);
}
}
word = word.substring(0, i) + original +
word.substring(i + 1);
}
}
/* Return an empty list if reaching the
target word is not possible */
if (!mpp.has(endWord))
return [];
// To store the answer
const ans = [];
// To store the possible sequence of transformations
const seq = [endWord];
// Backtracking step
this.dfs(endWord, beginWord, seq, mpp, ans);
// Return the computed result
return ans;
}
}
// Main function to test the Solution class
(function main() {
const beginWord = "der", endWord = "dfs";
const wordList = ["des", "der", "dfr", "dgt", "dfs"];
// Creating an instance of Solution class
const sol = new Solution();
/* Function call to determine number of steps
to reach from start word to target word */
const ans = sol.findSequences(beginWord, endWord, wordList);
// Output
console.log("The different sequences are:");
ans.forEach(seq => {
console.log(seq.join(" "));
});
})();
Complexity Analysis:
Time Complexity: O(N*M)
- Creating a set from the word list takes O(N).
- The queue can contain up to N words in the worst case. For each word, all possible M character positions are changed to 26 different letters taking overall O(N*M*26) time.
- In the worst case, the DFS might explore all possible sequences from the target word back to the start word.
Space Complexity: O(N2*M)
The set and map will store all the words each having M length taking O(N*M) space. The queue space will also be O(N*M) in the worst case. In the worst case, the result list will store all possible transformations ( which is N in the worst case) making the space requirement of O(N2*M)
Frequently Occurring Doubts
Q: What if startWord is not in wordList?
A: The transformation can still begin from startWord if it can reach an existing word in wordList. If startWord cannot transform into any valid word, return an empty list.
Q: Why use BFS instead of DFS for finding shortest paths?
A: BFS guarantees the shortest transformation sequence because it explores level by level. DFS does not guarantee this and may explore deeper paths unnecessarily.
Interview Followup Questions
Q: How would you modify this approach if words had different transformation costs?
A: If each word change had a different cost, Dijkstra’s Algorithm (shortest path with weighted edges) would be required instead of BFS.
Q: How would you handle dynamic word additions or deletions in wordList?
A: Instead of using a fixed wordList, we could use a Trie or a HashMap-based dynamic structure to allow fast insertions/deletions and efficient search operations.
Notes
Code
✅ Testcase
Input: {'endWord': 'dfs', 'wordList': ' ["des", "der", "dfr", "dgt", "dfs"] ', 'startWord': 'der'}
Expected:
der des dfs
der dfr dfs
der des dfs
der dfr dfs
Actual: -
Time: -
sec
Status: Waiting
Input: {'endWord': 'geek', 'wordList': '["geek", "gefk"]', 'startWord': 'gedk'}
Expected:
gedk geek
gedk geek
Actual: -
Time: -
sec
Status: Waiting
Input: {'endWord': 'xyz', 'wordList': ' ["abc", "ayc", "ayz", "xyz"]', 'startWord': 'abc'}
Expected:
abc ayc ayz xyz
abc ayc ayz xyz
Actual: -
Time: -
sec
Status: Waiting