Partition a set into two subsets with minimum absolute sum difference

This question is a slight modification of the problem discussed in the Subset Sum equal to target. Before discussing the approach for this question, it is important to understand what we did in the previous question of the Subset Sum equal to the target. There we found whether or not a subset exists in an array with a given target sum.

In this question, we need to partition the array into two subsets( say with sum S1 and S2) and we need to return the minimized absolute difference of S1 and S2. But do not need two variables for it. We can use a variable 'totSum', which stores the sum of all elements of the input array, and then we can simply say S2 = totSum - S1. Therefore we only need one variable S1.

From here try to find a subset in the array with a target as discussed in Subset Sum equal to the target.

Steps to form the recursive solution:

Express the problem in terms of indexes: The array will have an index but there is one more parameter “target”. So, we can say that initially, we need to find(n-1, target) which means that we need to find whether there exists a subset in the array from index 0 to n-1, whose sum is equal to the target.

So, f(ind, target) will check whether a subset exists in the array from index 0 to index 'ind' such that the sum of elements is equal to the target.

Try out all possible choices at a given index: As all the subsets needs to be generated, we will use the pick/non-pick technique.There will be two choices in each function call:

Do not include the current element in the subset: First try to find a subset without considering the current index element. For this, make a recursive call to f(ind-1,target).

Include the current element in the subset: Now try to find a subset by considering the current index element as part of subset. As the current element(arr[ind]) is included, the remaining target sum will be target - arr[ind]. Therefore, make a function call of f(ind-1,target-arr[ind]).

Note: Consider the current element in the subset only when the current element is less or equal to the target.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, target){
    not pick = f(ind-1, target)
    pick = false
    if(target <= arr[ind]){
        pick = f(ind-1, target - arr[ind])
    }
           
}

Return (pick || not pick): As we are looking for only one subset whose sum of elements is equal to target, if any of the one among 'pick' or 'not pick' returns true, it means the required subset is found so, return true.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, target){
   not pick = f(ind-1, target)
    pick = false
    if(target <= arr[ind]){
        pick = f(ind-1, target - arr[ind])
    }
    return (pick || not pick)    
}

Base cases: There will be tow base cases, First, when target == 0, it means that the subset is already found from the previous steps, so simply return true. Another, when ind==0, it means we are at the first element, so return arr[ind]==target. If the element is equal to the target it will return true else false.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to solve the subset sum problem recursively 
    bool func(int ind, int target, vector<int>& arr) {
        // Base case: If the target sum is 0, return true
        if (target == 0)
            return true;

        /* Base case: If we have considered all elements
        and the target is still not 0, return false*/
        if (ind == 0)
            return (arr[0] == target);

        // Exclude the current element
        bool notTaken = func(ind - 1, target, arr);

        /* Include the current element 
        if it doesn't exceed the target*/
        bool taken = false;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr);

        // Return the result
        return notTaken || taken;
    }
public:
    /* Function to find the minimum absolute
    difference between two subset sums*/
    int minDifference(vector<int>& arr, int n) {
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Calculate the subset sum for each 
        possible sum from 0 to the total sum*/
        for (int i = 0; i <= totSum; i++) {
            bool dummy = func(n - 1, i, arr);
        }

        int mini = 1e9;
        for (int i = 0; i <= totSum; i++) {
            if (func(n-1, i, arr) == true) {
                int diff = abs(i - (totSum - i));
                mini = min(mini, diff);
            }
        }
        return mini;
    }
};

int main() {
    vector<int> arr = {1, 2, 3, 4};
    int n = arr.size();

    //Create an instance of Solution class
    Solution sol;
    
    cout << "The minimum absolute difference is: " << sol.minDifference(arr, n);

    return 0;
}

import java.util.*;

class Solution {
    // Function to solve the subset sum problem Recursively
    private boolean func(int ind, int target, int[] arr) {
        // Base case: If the target sum is 0, return true
        if (target == 0)
            return true;

        /* Base case: If we have considered all elements 
        and the target is still not 0, return false*/
        if (ind == 0)
            return (arr[0] == target);
            
        // Exclude the current element
        boolean notTaken = func(ind - 1, target, arr);

        /* Include the current element 
        if it doesn't exceed the target*/
        boolean taken = false;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr);

        // Return the result
        return notTaken || taken;
    }

    /* Function to find the minimum absolute
    difference between two subset sums*/
    public int minDifference(int[] arr, int n) {
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Calculate the subset sum for each
        possible sum from 0 to the total sum*/
        for (int i = 0; i <= totSum; i++) {
            boolean dummy = func(n - 1, i, arr);
        }

        int mini = Integer.MAX_VALUE;
        for (int i = 0; i <= totSum; i++) {
            if (func(n - 1, i, arr) == true) {
                int diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }
        //Return the result
        return mini;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4};
        int n = arr.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        System.out.println("The minimum absolute difference is: " + sol.minDifference(arr, n));
    }
}
class Solution:
    # Function to solve the subset sum problem recursively
    def func(self, ind, target, arr):
        # Base case: If the target sum is 0, return true
        if target == 0:
            return True

        """ Base case: If we have considered all elements 
        and the target is still not 0, return false"""
        if ind == 0:
            return arr[0] == target

        # Exclude the current element
        not_taken = self.func(ind - 1, target, arr)

        """ Include the current element 
        if it doesn't exceed the target"""
        taken = False
        if arr[ind] <= target:
            taken = self.func(ind - 1, target - arr[ind], arr)

        # Return the result
        return not_taken or taken

    """ Function to find the minimum absolute
    difference between two subset sums"""
    def minDifference(self, arr, n):
        tot_sum = 0

        # Calculate the total sum of the array
        for i in range(n):
            tot_sum += arr[i]

        """ Calculate the subset sum for each
        possible sum from 0 to the total sum"""
        for i in range(tot_sum + 1):
            dummy = self.func(n - 1, i, arr)

        mini = float('inf')
        for i in range(tot_sum + 1):
            if self.func(n - 1, i, arr):
                diff = abs(i - (tot_sum - i))
                mini = min(mini, diff)

        return mini

if __name__ == "__main__":
    arr = [1, 2, 3, 4]
    n = len(arr)

    # Create an instance of Solution class
    sol = Solution()

    print("The minimum absolute difference is:", sol.minDifference(arr, n))
class Solution {
    // Function to solve the subset sum problem recursively
    func(ind, target, arr) {
        // Base case: If the target sum is 0, return true
        if (target === 0)
            return true;

        /* Base case: If we have considered all elements 
        and the target is still not 0, return false*/
        if (ind === 0)
            return arr[0] === target;

        // Exclude the current element
        let notTaken = this.func(ind - 1, target, arr);

        /* Include the current element 
        if it doesn't exceed the target*/
        let taken = false;
        if (arr[ind] <= target)
            taken = this.func(ind - 1, target - arr[ind], arr);

        // Return the result
        return notTaken || taken;
    }

    /* Function to find the minimum absolute
    difference between two subset sums*/
    minDifference(arr, n) {
        let totSum = 0;

        // Calculate the total sum of the array
        for (let i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Calculate the subset sum for each 
        possible sum from 0 to the total sum*/
        for (let i = 0; i <= totSum; i++) {
            let dummy = this.func(n - 1, i, arr);
        }

        let mini = Number.MAX_VALUE;
        for (let i = 0; i <= totSum; i++) {
            if (this.func(n - 1, i, arr)) {
                let diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }
        //Return the result
        return mini;
    }
}

const arr = [1, 2, 3, 4];
const n = arr.length;

// Create an instance of Solution class
const sol = new Solution();

console.log("The minimum absolute difference is:", sol.minDifference(arr, n));

Time Complexity: O(2^(N))+O(N)+O(N), where N is the length of the array. As, for each index, ther are two possible options.

Space Complexity:O(N), at maximum the depth of the recursive stack can go upto N.

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'target' only values between 0 to target. Therefore, we need 2D dp array.

The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to solve the subset sum problem 
    bool func(int ind, int target, vector<int>& arr, vector<vector<int>>& dp) {
        // Base case: If the target sum is 0, return true
        if (target == 0)
            return dp[ind][target] = true;

        /* Base case: If we have considered all elements
        and the target is still not 0, return false*/
        if (ind == 0)
            return dp[ind][target] = (arr[0] == target);
            
        /* If the result for this state 
        is already calculated, return it*/
        if (dp[ind][target] != -1)
            return dp[ind][target];

        // Exclude the current element
        bool notTaken = func(ind - 1, target, arr, dp);

        /* Include the current element 
        if it doesn't exceed the target*/
        bool taken = false;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr, dp);

        // Return the result
        return dp[ind][target] = notTaken || taken;
    }
public:
    /* Function to find the minimum absolute
    difference between two subset sums*/
    int minDifference(vector<int>& arr, int n) {
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }
        
        /* Initialize a DP table to store the
        results of the subset sum problem*/
        vector<vector<int>> dp(n, vector<int>(totSum + 1, -1));
        
        /* Calculate the subset sum for each 
        possible sum from 0 to the total sum*/
        for (int i = 0; i <= totSum; i++) {
            bool dummy = func(n - 1, i, arr, dp);
        }

        int mini = 1e9;
        for (int i = 0; i <= totSum; i++) {
            if (dp[n-1][i] == true) {
                int diff = abs(i - (totSum - i));
                mini = min(mini, diff);
            }
        }
        return mini;
    }
};

int main() {
    vector<int> arr = {1, 2, 3, 4};
    int n = arr.size();

    //Create an instance of Solution class
    Solution sol;
    
    cout << "The minimum absolute difference is: " << sol.minDifference(arr, n);

    return 0;
}

import java.util.*;

class Solution {
    // Function to solve the subset sum problem
    private boolean func(int ind, int target, int[] arr, int[][] dp) {
        // Base case: If the target sum is 0, return true
        if (target == 0)
            return true;

        /* Base case: If we have considered all elements
        and the target is still not 0, return false*/
        if (ind == 0)
            return arr[0] == target;

        /* If the result for this state 
        is already calculated, return it*/
        if (dp[ind][target] != -1)
            return dp[ind][target] == 1;

        // Exclude the current element
        boolean notTaken = func(ind - 1, target, arr, dp);

        /* Include the current element 
        if it doesn't exceed the target*/
        boolean taken = false;
        if (arr[ind] <= target)
            taken = func(ind - 1, target - arr[ind], arr, dp);

        // Store and return the result
        dp[ind][target] = (notTaken || taken) ? 1 : 0;
        return notTaken || taken;
    }

    /* Function to find the minimum absolute
    difference between two subset sums*/
    public int minDifference(int[] arr, int n) {
        if (n == 1) {
            // If there's only one element, no subsets can be divided, so the result is 0
            return arr[0];
        }
        
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }
        
        /* Initialize a DP table to store the
        results of the subset sum problem*/
        int[][] dp = new int[n][totSum + 1];
        for (int[] row : dp)
            Arrays.fill(row, -1);
        
        /* Calculate the subset sum for each 
        possible sum from 0 to the total sum*/
        for (int i = 0; i <= totSum; i++) {
            boolean dummy = func(n - 1, i, arr, dp);
        }

        int mini = Integer.MAX_VALUE;
        for (int i = 0; i <= totSum; i++) {
            if (dp[n-1][i] == 1) {
                int diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }
        return mini;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4};
        int n = arr.length;

        // Create an instance of Solution class
        Solution sol = new Solution();
        
        System.out.println("The minimum absolute difference is: " + sol.minDifference(arr, n));
    }
}
class Solution:
    # Function to solve the subset sum problem
    def func(self, ind, target, arr, dp):
        # Base case: If the target sum is 0, return true
        if target == 0:
            dp[ind][target] = True
            return True

        """ Base case: If we have considered all elements 
        and the target is still not 0, return false"""
        if ind == 0:
            dp[ind][target] = (arr[0] == target)
            return dp[ind][target]

        """ If the result for this state is
        already calculated, return it"""
        if dp[ind][target] != -1:
            return dp[ind][target]

        # Exclude the current element
        not_taken = self.func(ind - 1, target, arr, dp)

        """ Include the current element if 
        it doesn't exceed the target"""
        taken = False
        if arr[ind] <= target:
            taken = self.func(ind - 1, target - arr[ind], arr, dp)

        # Return the result
        dp[ind][target] = not_taken or taken
        return dp[ind][target]

    """ Function to find the minimum absolute
    difference between two subset sums"""
    def minDifference(self, arr, n):
        tot_sum = 0

        # Calculate the total sum of the array
        for i in range(n):
            tot_sum += arr[i]

        """ Initialize a DP table to store the
        results of the subset sum problem"""
        dp = [[-1 for _ in range(tot_sum + 1)] for _ in range(n)]

        """ Calculate the subset sum for each 
        possible sum from 0 to the total sum"""
        for i in range(tot_sum + 1):
            dummy = self.func(n - 1, i, arr, dp)

        mini = float('inf')
        for i in range(tot_sum + 1):
            if dp[n - 1][i] == True:
                diff = abs(i - (tot_sum - i))
                mini = min(mini, diff)

        return mini

if __name__ == "__main__":
    arr = [1, 2, 3, 4]
    n = len(arr)

    # Create an instance of Solution class
    sol = Solution()

    print("The minimum absolute difference is:", sol.minDifference(arr, n))
class Solution {
    // Function to solve the subset sum problem 
    func(ind, target, arr, dp) {
        // Base case: If the target sum is 0, return true
        if (target === 0) {
            dp[ind][target] = true;
            return true;
        }

        /* Base case: If we have considered all elements
        and the target is still not 0, return false*/
        if (ind === 0) {
            dp[ind][target] = (arr[0] === target);
            return dp[ind][target];
        }

        /* If the result for this state is
        already calculated, return it*/
        if (dp[ind][target] !== -1)
            return dp[ind][target];

        // Exclude the current element
        let notTaken = this.func(ind - 1, target, arr, dp);

        /* Include the current element if 
        it doesn't exceed the target*/
        let taken = false;
        if (arr[ind] <= target)
            taken = this.func(ind - 1, target - arr[ind], arr, dp);

        // Return the result
        dp[ind][target] = notTaken || taken;
        return dp[ind][target];
    }

    /* Function to find the minimum absolute
    difference between two subset sums*/
    minDifference(arr, n) {
        let totSum = 0;

        // Calculate the total sum of the array
        for (let i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Initialize a DP table to store 
        the results of the subset sum problem*/
        let dp = Array.from({ length: n }, () => Array(totSum + 1).fill(-1));

        /* Calculate the subset sum for each 
        possible sum from 0 to the total sum*/
        for (let i = 0; i <= totSum; i++) {
            let dummy = this.func(n - 1, i, arr, dp);
        }

        let mini = Number.MAX_VALUE;
        for (let i = 0; i <= totSum; i++) {
            if (dp[n - 1][i] === true) {
                let diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }

        return mini;
    }
}

const arr = [1, 2, 3, 4];
const n = arr.length;

// Create an instance of Solution class
const sol = new Solution();

console.log("The minimum absolute difference is:", sol.minDifference(arr, n));

Complexity Analysis:

Time Complexity: O(N*sum)+O(N) +O(N), There are 'N*sum' states therefore at max ‘N*sum’ new problems will be solved.

Space Complexity:O(N*sum) + O(N), As we are using a recursion stack space(O(N)) and a 2D array ( O(N*sum)).

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

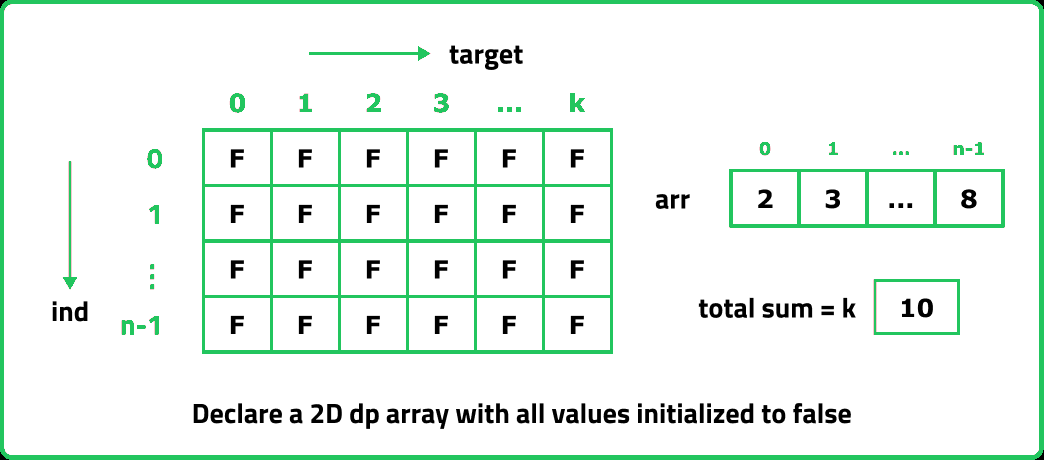
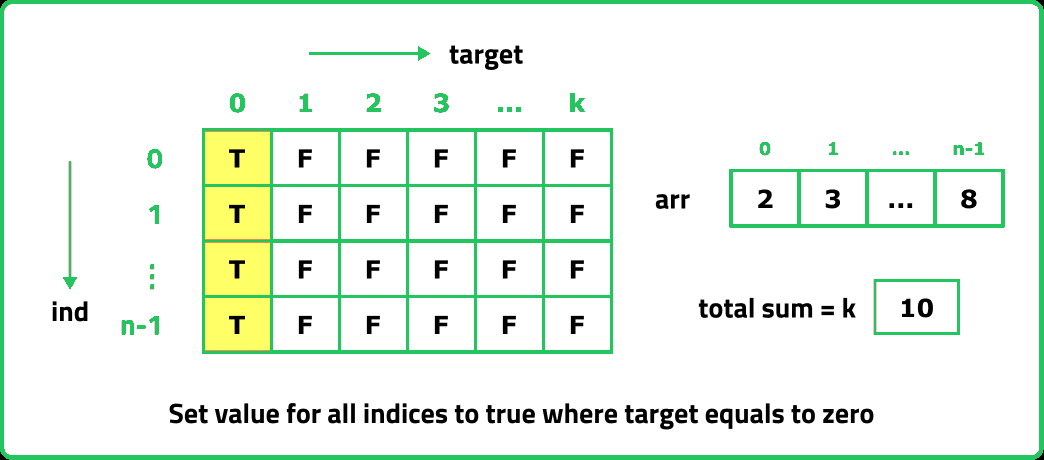
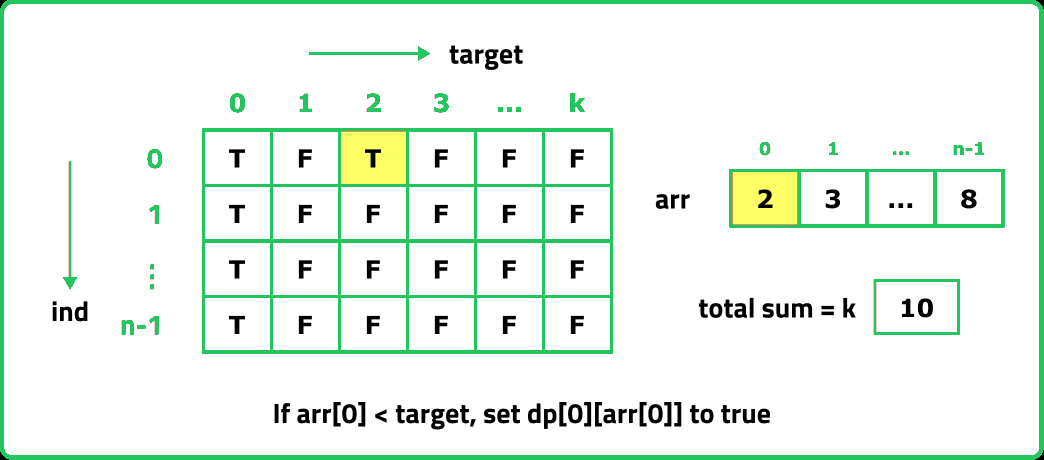
Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n) and including 0 its n, where n is the size of array, for 'target' can have any values between 0 to 'target'. So we need a 2D dp array. Set its type as int and initialize it as 0.

Setting Base Cases in the Array: In the recursive code, our base condition was when target == 0, it means the required subset is found and we were returning 1. So, set '1' in the dp array for every index where target = 0.

The first row dp[0][] indicates that only the first element of the array is considered, therefore for the target value equal to arr[0], only cell with that target will be true, so explicitly set dp[0][arr[0]] =1, (dp[0][arr[0]] means that we are considering the first element of the array with the target equal to the first element itself). Please note that it can happen that arr[0]>target, so we first check it: if(arr[0]<=target) then set dp[0][arr[0]] = 1

Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.

Returning the answer: At last dp[n-1][target] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    /* Function to find the minimum absolute
    difference between two subset sums*/
    int minDifference(vector<int>& arr, int n) {
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Initialize a DP table to store the
        results of the subset sum problem*/
        vector<vector<bool>> dp(n, vector<bool>(totSum + 1, false));

        /* Base case: If no elements are 
        selected (sum is 0), it's a valid subset*/
        for (int i = 0; i < n; i++) {
            dp[i][0] = true;
        }

        /* Initialize the first row based  
        on the first element of the array*/
        if (arr[0] <= totSum)
            dp[0][totSum] = true;

        // Fill in the DP table using bottom-up approach
        for (int ind = 1; ind < n; ind++) {
            
            for (int target = 1; target <= totSum; target++) {
                // Exclude the current element
                bool notTaken = dp[ind - 1][target];

                /* Include the current element 
                if it doesn't exceed the target*/
                bool taken = false;
                if (arr[ind] <= target)
                    taken = dp[ind - 1][target - arr[ind]];

                dp[ind][target] = notTaken || taken;
            }
        }

        int mini = 1e9;
        for (int i = 0; i <= totSum; i++) {
            if (dp[n - 1][i] == true) {
                /* Calculate the absolute difference
                between two subset sums*/
                int diff = abs(i - (totSum - i));
                mini = min(mini, diff);
            }
        }
        //Return the result
        return mini;
    }
};
int main() {
    vector<int> arr = {1, 2, 3, 4};
    int n = arr.size();
    
    //Create an instance of Solution class
    Solution sol;
    
    cout << "The minimum absolute difference is: " << sol.minDifference(arr, n);

    return 0;
}

import java.util.*;

class Solution {
    /* Function to find the minimum absolute
    difference between two subset sums */
    public int minDifference(int[] arr, int n) {
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Initialize a DP table to store the
        results of the subset sum problem */
        boolean[][] dp = new boolean[n][totSum + 1];

        /* Base case: If no elements are 
        selected (sum is 0), it's a valid subset */
        for (int i = 0; i < n; i++) {
            dp[i][0] = true;
        }

        /* Initialize the first row based  
        on the first element of the array */
        if (arr[0] <= totSum)
            dp[0][arr[0]] = true;

        // Fill in the DP table using bottom-up approach
        for (int ind = 1; ind < n; ind++) {
            for (int target = 1; target <= totSum; target++) {
                // Exclude the current element
                boolean notTaken = dp[ind - 1][target];

                /* Include the current element 
                if it doesn't exceed the target */
                boolean taken = false;
                if (arr[ind] <= target)
                    taken = dp[ind - 1][target - arr[ind]];

                dp[ind][target] = notTaken || taken;
            }
        }

        int mini = Integer.MAX_VALUE;
        for (int i = 0; i <= totSum; i++) {
            if (dp[n - 1][i]) {
                /* Calculate the absolute difference
                between two subset sums */
                int diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }
        //Return the result
        return mini;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4};
        int n = arr.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        System.out.println("The minimum absolute difference is: " + sol.minDifference(arr, n));
    }
}
class Solution:
    """ Function to find the minimum absolute
    difference between two subset sums"""
    def minDifference(self, arr, n):
        totSum = sum(arr)

        """ Initialize a DP table to store the
        results of the subset sum problem"""
        dp = [[False] * (totSum + 1) for _ in range(n)]

        """ Base case: If no elements are 
        selected (sum is 0), it's a valid subset"""
        for i in range(n):
            dp[i][0] = True

        """ Initialize the first row based 
        on the first element of the array"""
        if arr[0] <= totSum:
            dp[0][arr[0]] = True

        # Fill in the DP table using bottom-up approach
        for ind in range(1, n):
            for target in range(1, totSum + 1):
                # Exclude the current element
                notTaken = dp[ind - 1][target]

                """ Include the current element if
                it doesn't exceed the target"""
                taken = False
                if arr[ind] <= target:
                    taken = dp[ind - 1][target - arr[ind]]

                dp[ind][target] = notTaken or taken

        mini = float('inf')
        for i in range(totSum + 1):
            if dp[n - 1][i]:
                """ Calculate the absolute difference
                between two subset sums"""
                diff = abs(i - (totSum - i))
                mini = min(mini, diff)

        return mini

arr = [1, 2, 3, 4]
n = len(arr)

#Create an instance of Solution class
sol = Solution()

print("The minimum absolute difference is:", sol.minDifference(arr, n))
class Solution {
    /* Function to find the minimum absolute
    difference between two subset sums*/
    minDifference(arr, n) {
        let totSum = arr.reduce((a, b) => a + b, 0);

        /* Initialize a DP table to store the
        results of the subset sum problem*/
        const dp = Array.from({ length: n }, () => Array(totSum + 1).fill(false));

        /* Base case: If no elements are 
        selected (sum is 0), it's a valid subset*/
        for (let i = 0; i < n; i++) {
            dp[i][0] = true;
        }

        /* Initialize the first row based 
        on the first element of the array*/
        if (arr[0] <= totSum) {
            dp[0][arr[0]] = true;
        }

        // Fill in the DP table using bottom-up approach
        for (let ind = 1; ind < n; ind++) {
            for (let target = 1; target <= totSum; target++) {
                // Exclude the current element
                const notTaken = dp[ind - 1][target];

                /* Include the current element 
                if it doesn't exceed the target*/
                let taken = false;
                if (arr[ind] <= target) {
                    taken = dp[ind - 1][target - arr[ind]];
                }

                dp[ind][target] = notTaken || taken;
            }
        }

        let mini = Number.MAX_VALUE;
        for (let i = 0; i <= totSum; i++) {
            if (dp[n - 1][i]) {
                /* Calculate the absolute difference
                between two subset sums*/
                const diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }

        return mini;
    }
}

const arr = [1, 2, 3, 4];
const n = arr.length;

//Create an instance of Solution class
const sol = new Solution();

console.log("The minimum absolute difference is:", sol.minDifference(arr, n));

Complexity Analysis:

Time Complexity: O(N*sum)+O(N) +O(N), Where sum is the total sum of elements of the array. There are two nested loops that account for O(N*sum), at starting we are running a for loop to calculate totSum, and at last a for loop to traverse the last row.

Space Complexity:O(N*sum), Where sum is the total sum of elements of the array. As a 2D array of size N*sum is used.

If we observe the relation, dp[ind][target] = dp[ind-1][target] || dp[ind-1][target-arr[ind]]. We see that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it.

Steps to space optimize the tabulation code:

Initialize the DP Table: Initialize a boolean vector 'prev' of size 'totSum + 1' to store whether a particular subset sum is achievable. Set prev[0] to true because a subset sum of 0 is always achievable with an empty subset.

If the first element of the array arr[0] is less than or equal to totSum, mark prev[arr[0]] as true, indicating that a subset sum equal to arr[0] is achievable.

Update the DP Table: Iterate through each element of the array starting from the second element. For each element, create a new boolean vector cur to represent the current state of achievable subset sums. Update cur based on whether each target sum can be achieved either by excluding or including the current element. After processing each element, update prev to be cur for the next iteration.
Find the Minimum Absolute Difference: Initialize a variable mini to a large value (1e9) to keep track of the minimum absolute difference found. Iterate through all possible subset sums stored in prev. For each achievable subset sum i, calculate the absolute difference between i and the complement subset sum (totSum - i).
Update mini with the minimum of the current difference and mini. Finally, return the minimum absolute difference found.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    /* Function to find the minimum absolute
    difference between two subset sums*/
    int minDifference(vector<int>& arr, int n) {
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Initialize a boolean vector 'prev' to 
        represent the previous row of the DP table*/
        vector<bool> prev(totSum + 1, false);

        /* Base case: If no elements are 
        selected (sum is 0), it's a valid subset*/
        prev[0] = true;

        /* Initialize the first row based 
        on the first element of the array*/
        if (arr[0] <= totSum)
            prev[arr[0]] = true;

        // Fill in the DP table using bottom-up approach
        for (int ind = 1; ind < n; ind++) {
            /* Initialize a boolean vector 'cur' to 
            represent the current row of the DP table*/
            vector<bool> cur(totSum + 1, false);
            
            cur[0] = true;

            for (int target = 1; target <= totSum; target++) {
                // Exclude the current element
                bool notTaken = prev[target];

                /* Include the current element
                if it doesn't exceed the target*/
                bool taken = false;
                if (arr[ind] <= target)
                    taken = prev[target - arr[ind]];

                cur[target] = notTaken || taken;
            }

            // Set 'cur' as the 'prev' for the next iteration
            prev = cur;
        }

        int mini = 1e9;
        for (int i = 0; i <= totSum; i++) {
            if (prev[i] == true) {
                /* Calculate the absolute 
                difference between two subset sums*/
                int diff = abs(i - (totSum - i));
                mini = min(mini, diff);
            }
        }
        return mini;
    }
};
int main() {
    vector<int> arr = {1, 2, 3, 4};
    int n = arr.size();
    
    //Create an instance of Solution class
    Solution sol;

    cout << "The minimum absolute difference is: " << sol.minDifference(arr, n);

    return 0;
}

import java.util.*;

class Solution {
    /* Function to find the minimum absolute
    difference between two subset sums */
    public int minDifference(int[] arr, int n) {
        int totSum = 0;

        // Calculate the total sum of the array
        for (int i = 0; i < n; i++) {
            totSum += arr[i];
        }

        /* Initialize a boolean vector 'prev' to
        represent the previous row of the DP table */
        boolean[] prev = new boolean[totSum + 1];
        Arrays.fill(prev, false);

        /* Base case: If no elements are
        selected (sum is 0), it's a valid subset */
        prev[0] = true;

        /* Initialize the first row based
        on the first element of the array */
        if (arr[0] <= totSum)
            prev[arr[0]] = true;

        // Fill in the DP table using bottom-up approach
        for (int ind = 1; ind < n; ind++) {
            /* Initialize a boolean vector 'cur' to
            represent the current row of the DP table */
            boolean[] cur = new boolean[totSum + 1];
            Arrays.fill(cur, false);
            cur[0] = true;

            for (int target = 1; target <= totSum; target++) {
                // Exclude the current element
                boolean notTaken = prev[target];

                /* Include the current element
                if it doesn't exceed the target */
                boolean taken = false;
                if (arr[ind] <= target)
                    taken = prev[target - arr[ind]];

                cur[target] = notTaken || taken;
            }

            // Set 'cur' as the 'prev' for the next iteration
            prev = cur;
        }

        int mini = Integer.MAX_VALUE;
        for (int i = 0; i <= totSum; i++) {
            if (prev[i]) {
                /* Calculate the absolute
                difference between two subset sums */
                int diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }
        return mini;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4};
        int n = arr.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        System.out.println("The minimum absolute difference is: " + sol.minDifference(arr, n));
    }
}
class Solution:
    """ Function to find the minimum absolute
    difference between two subset sums"""
    def minDifference(self, arr, n):
        totSum = sum(arr)

        """ Initialize a boolean vector 'prev' to
        represent the previous row of the DP table"""
        prev = [False] * (totSum + 1)
        prev[0] = True

        """ Initialize the first row based
        on the first element of the array"""
        if arr[0] <= totSum:
            prev[arr[0]] = True

        # Fill in the DP table using bottom-up approach
        for ind in range(1, n):
            """ Initialize a boolean vector 'cur' to
            represent the current row of the DP table"""
            cur = [False] * (totSum + 1)
            cur[0] = True

            for target in range(1, totSum + 1):
                # Exclude the current element
                notTaken = prev[target]

                """ Include the current element if
                it doesn't exceed the target"""
                taken = False
                if arr[ind] <= target:
                    taken = prev[target - arr[ind]]

                cur[target] = notTaken or taken

            # Set 'cur' as the 'prev' for the next iteration
            prev = cur

        mini = float('inf')
        for i in range(totSum + 1):
            if prev[i]:
                """ Calculate the absolute 
                difference between two subset sums"""
                diff = abs(i - (totSum - i))
                mini = min(mini, diff)

        return mini

arr = [1, 2, 3, 4]
n = len(arr);

#Create an instance of Solution class
sol = Solution()

print("The minimum absolute difference is:", sol.minDifference(arr, n))
class Solution {
    /* Function to find the minimum absolute
    difference between two subset sums*/
    minDifference(arr, n) {
        let totSum = arr.reduce((a, b) => a + b, 0);

        /* Initialize a boolean vector 'prev' to
        represent the previous row of the DP table*/
        const prev = new Array(totSum + 1).fill(false);
        prev[0] = true;

        /* Initialize the first row based
        on the first element of the array*/
        if (arr[0] <= totSum) {
            prev[arr[0]] = true;
        }

        // Fill in the DP table using bottom-up approach
        for (let ind = 1; ind < n; ind++) {
            /* Initialize a boolean vector 'cur' to
            represent the current row of the DP table*/
            const cur = new Array(totSum + 1).fill(false);
            cur[0] = true;

            for (let target = 1; target <= totSum; target++) {
                // Exclude the current element
                const notTaken = prev[target];

                /* Include the current element 
                if it doesn't exceed the target*/
                let taken = false;
                if (arr[ind] <= target) {
                    taken = prev[target - arr[ind]];
                }

                cur[target] = notTaken || taken;
            }

            // Set 'cur' as the 'prev' for the next iteration
            prev.splice(0, prev.length, ...cur);
        }

        let mini = Number.MAX_VALUE;
        for (let i = 0; i <= totSum; i++) {
            if (prev[i]) {
                /* Calculate the absolute 
                difference between two subset sums*/
                const diff = Math.abs(i - (totSum - i));
                mini = Math.min(mini, diff);
            }
        }
   
        return mini;
    }
}

const arr = [1, 2, 3, 4];
const n = arr.length;

//Create an instance of Solution class
const sol = new Solution();

console.log("The minimum absolute difference is:", sol.minDifference(arr,n));

Complexity Analysis:

Time Complexity: O(N*sum) + O(N) + O(N), There are two nested loops that account for O(N*sum), at starting we are running a for loop to calculate totSum and at last a for loop to traverse the last row.

Space Complexity:O(sum), Where sum is the total sum of elements of the array. We are using an external array of size ‘sum+1’ to store only one row.

Problem List

Partition a set into two subsets with minimum absolute sum difference

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

Steps to space optimize the tabulation code:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code