Rotate matrix by 90 degrees

Arrays FAQs(Medium) Medium

One interesting application of this problem can be found in image processing
Many image-editing software or applications use rotation algorithms similar to this to adjust or manipulate images
For instance, when you rotate an image 90 degrees clockwise on your smartphone or computer, programs effectively apply a similar method in the background

Given an N * N 2D integer matrix, rotate the matrix by 90 degrees clockwise.

The rotation must be done in place, meaning the input 2D matrix must be modified directly.

Examples:

Input: matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

Output: matrix = [[7, 4, 1], [8, 5, 2], [9, 6, 3]]

Input: matrix = [[0, 1, 1, 2], [2, 0, 3, 1], [4, 5, 0, 5], [5, 6, 7, 0]]

Output: matrix = [[5, 4, 2, 0], [6, 5, 0, 1], [7, 0, 3, 1], [0, 5, 1, 2]]

Input: matrix = [[1, 1, 2], [5, 3, 1], [5, 3, 5]]

Constraints

n == matrix.length.
n == matrix[i].length.
1 <= n <= 100.
-10⁴ <= matrix[i][j] <= 10⁴

Hints

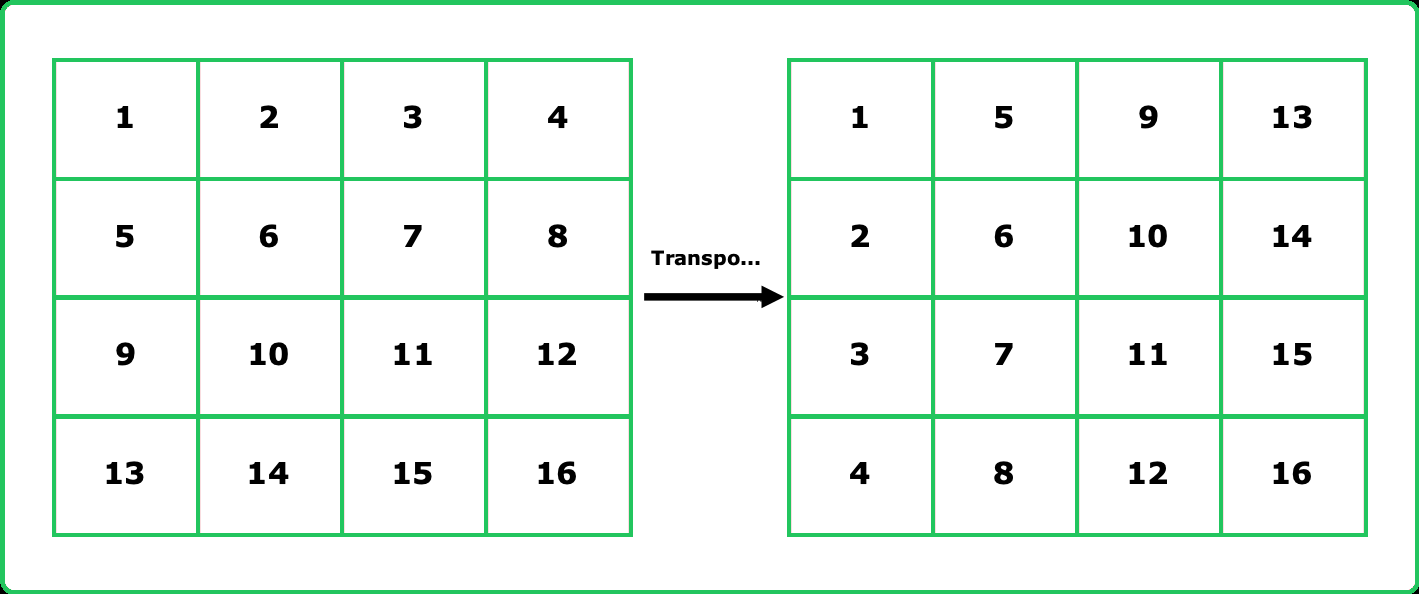
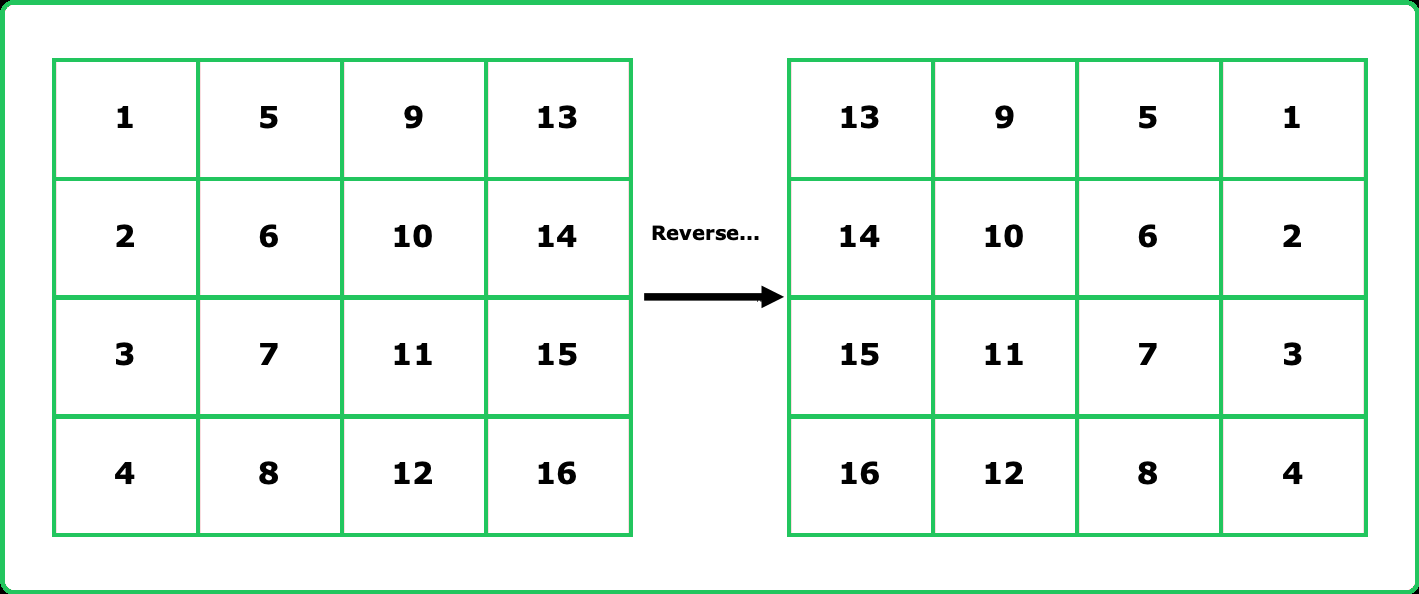
Swap elements such that matrix[i][j] becomes matrix[j][i]. Reverse the order of elements in each row to complete the rotation.
Alternatively, rotate the matrix in layers, starting from the outermost layer and moving inward. For each layer, shift elements in groups of four.

Company Tags

Snowflake Epic Games Freshworks Bungie Robinhood Boston Consulting Group OYO Rooms Philips Healthcare Ernst & Young Visa Lyft Texas Instruments McKinsey & Company Chewy DoorDash Goldman Sachs Pinterest Wayfair Roblox Ubisoft Splunk Target Swiggy American Express Intel TCS Cognizant Accenture Infosys Capgemini Wipro

Intuition

The naive way is to take another dummy matrix of row and column same as original matrix. Then, take the first row of the original matrix and place it in the last column of the dummy matrix. Next, take the second row of the original matrix and place it in the second last column of the dummy matrix, continuing this process until the last row of the original matrix is placed in the first column of the dummy matrix.

Finally, copy the elements of the dummy matrix back to the original matrix. This procedure ensures that the original matrix is rotated by 90 degrees clockwise.

Approach

initialize a dummy matrix to store the elemens in rotated order.

Iterate in the array using nested for loops say (i) for row and (j) for columns and take the elements of the first row of matrix, put it in last column of the dummy matrix. Repeat this process until index i crosses sizeOfArray

Again, copy the elements of the dummy matrix to the original matrix and finally, return the original matrix.

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to rotate the given 
    matrix by 90 degrees clockwise*/
    void rotateMatrix(vector<vector<int>>& matrix) {
        
        /* Get the size of the matrix 
        (assuming it's a square matrix)*/
        int n = matrix.size();
        
        // Initialize new matrix to store rotated values
        vector<vector<int>> rotated(n, vector<int>(n, 0)); 
        
        // Iterate through elements of original matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                
                /* Rotate the element to its new 
                position in the rotated matrix
                New position is (j, n - i - 1) 
                in the rotated matrix*/
                
                rotated[j][n - i - 1] = matrix[i][j];
            }
        }
        
        //copy rotated elements to matrix
        for(int i = 0; i < rotated.size(); i++){
            for(int j = 0; j < rotated[0].size(); j++){
                matrix[i][j] = rotated[i][j];
            }
        }
    
    }
};

int main() {
    vector<vector<int>> arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}; 
    
    // Create an instance of the Solution class
    Solution sol; 
    
    sol.rotate(arr); 
    
    // Print the rotated matrix
    cout << "Rotated Image" << endl;
    for (int i = 0; i < arr.size(); i++) {
        for (int j = 0; j < arr[0].size(); j++) {
            cout << arr[i][j] << " "; 
        }
        cout << endl; 
    }

    return 0;
}
import java.util.*;

class Solution {
    //Function to rotate the given matrix by 90 degrees clockwise
     
    public void rotateMatrix(int[][] matrix) {
        int n = matrix.length;
        
        // Initialize new matrix to store rotated values
        int[][] rotated = new int[n][n];
        
        // Perform rotation logic
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                rotated[j][n - i - 1] = matrix[i][j];
            }
        }
        
        // Copy rotated elements tooriginal matrix
        for (int i = 0; i < n; i++) {
            System.arraycopy(rotated[i], 0, matrix[i], 0, n);
        }
    }

    public static void main(String[] args) {
        int[][] arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
        
        // Create an instance of the Solution class
        Solution sol = new Solution();
        
        // Rotate the matrix
        sol.rotate(arr);
        
        // Print the rotated matrix
        System.out.println("Rotated Image");
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[0].length; j++) {
                System.out.print(arr[i][j] + " ");
            }
            System.out.println();
        }
    }
}
from typing import List

class Solution:
    #Function to rotate the given matrix by 90 degrees clockwise
    
    def rotateMatrix(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        
        # Initialize new matrix to store rotated values
        rotated = [[0] * n for _ in range(n)]
        
        # Perform rotation logic
        for i in range(n):
            for j in range(n):
                rotated[j][n - i - 1] = matrix[i][j]
        
        # Copy rotated elements back to original matrix
        for i in range(n):
            matrix[i] = rotated[i]

if __name__ == "__main__":
    arr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
    
    # Create an instance of the Solution class
    sol = Solution()
    
    # Rotate the matrix
    sol.rotate(arr)
    
    # Print the rotated matrix
    print("Rotated Image:")
    for row in arr:
        print(" ".join(map(str, row)))
class Solution {
    //Function to rotate the given matrix by 90 degrees clockwise
    
    rotateMatrix(matrix) {
        let n = matrix.length;
        
        // Initialize new matrix to store rotated values
        let rotated = new Array(n).fill().map(() => new Array(n).fill(0));
        
        // Perform rotation logic
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < n; j++) {
                rotated[j][n - i - 1] = matrix[i][j];
            }
        }
        
        // Copy rotated elements back to original matrix
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < n; j++) {
                matrix[i][j] = rotated[i][j];
            }
        }
    }
}

let arr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]];
let sol = new Solution();

// Rotate the matrix
sol.rotate(arr);

// Print the rotated matrix
console.log("Rotated Image:");
for (let row of arr) {
    console.log(row.join(" "));
}

Complexity Analysis

Time Complexity: O(N²) +O(N²), to linearly iterate and put elements into dummy matrix and another O(N²) to copy elements of dummy matrix back to original matrix. Space Complexity: O(N²), to store the elements in the dummy matrix.

Intuition

The optimal way is to find the transpose of the matrix, which ensures that the first row of the matrix becomes the first column, the second row becomes the second column, and so on. Then, reverse each row. This method ensures that the array is rotated 90 degrees without using extra space.

Approach

Run nested for loop say(i) for row and (j) for column to iterate the matrix and transpose the matrix to change rows to columns and columns to rows.

Loop again to reverse each row of the matrix. Finally return the matrix.

Dry Run

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Rotate the given matrix
    by 90 degrees clockwise.
    */
    void rotateMatrix(vector<vector<int>>& matrix) {
        int n = matrix.size();
        
        // Transpose the matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
        
        // Reverse each row of the matrix
        for (int i = 0; i < n; i++) {
            reverse(matrix[i].begin(), matrix[i].end());
        }
    }
};

int main() {
    vector<vector<int>> arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
    
    // Create an instance of the Solution class
    Solution sol;
    
    // Rotate the matrix
    sol.rotate(arr);
    
    // Output the rotated matrix
    cout << "Rotated Image" << endl;
    for (int i = 0; i < arr.size(); i++) {
        for (int j = 0; j < arr[0].size(); j++) {
            cout << arr[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}
class Solution {
    //Rotate the given matrix by 90 degrees clockwise.
    
    public void rotateMatrix(int[][] matrix) {
        int n = matrix.length;
        
        // Transpose the matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                
                // Swap elements across the diagonal
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
                
            }
        }
        
        // Reverse each row of the matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n / 2; j++) {
                
                // Swap elements symmetrically
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][n - 1 - j];
                matrix[i][n - 1 - j] = temp;
                
            }
        }
    }

    public static void main(String[] args) {
        int[][] arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
        
        // Create an instance of the Solution class
        Solution sol = new Solution();
        
        // Rotate the matrix
        sol.rotate(arr);
        
        // Output the rotated matrix
        System.out.println("Rotated Image:");
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[0].length; j++) {
                System.out.print(arr[i][j] + " ");
            }
            System.out.println();
        }
    }
}
from typing import List

class Solution:
    # Rotate the given matrix by 90 degrees clockwise.
    def rotateMatrix(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        
        # Transpose the matrix
        for i in range(n):
            for j in range(i):
                # Swap elements across the diagonal
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        
        # Reverse each row of the matrix
        for i in range(n):
            for j in range(n // 2):
                # Swap elements symmetrically
                matrix[i][j], matrix[i][n - 1 - j] = matrix[i][n - 1 - j], matrix[i][j]

if __name__ == "__main__":
    arr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
    
    # Create an instance of the Solution class
    sol = Solution()
    
    # Rotate the matrix
    sol.rotate(arr)
    
    # Output the rotated matrix
    print("Rotated Image:")
    for row in arr:
        print(" ".join(map(str, row)))
class Solution {
    // Rotate the given matrix by 90 degrees clockwise.
    rotateMatrix(matrix) {
        let n = matrix.length;
        
        // Transpose the matrix
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < i; j++) {
                // Swap elements across the diagonal
                [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
            }
        }
        
        // Reverse each row of the matrix
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < Math.floor(n / 2); j++) {
                // Swap elements symmetrically
                [matrix[i][j], matrix[i][n - 1 - j]] = [matrix[i][n - 1 - j], matrix[i][j]];
            }
        }
    }
}

// Example usage:
let arr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]];

// Create an instance of the Solution class
let sol = new Solution();

// Rotate the matrix
sol.rotate(arr);

// Output the rotated matrix
console.log("Rotated Image:");
for (let row of arr) {
    console.log(row.join(" "));
}

Complexity Analysis

Time Complexity: O(N²) +O(N²), to linearly iterate and find transpose of the matrix and another O(N²) to find the reverse of each row. Space Complexity: O(1), as no extra space is being used.

Code

Problem List

Rotate matrix by 90 degrees

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Approach

Complexity Analysis

Intuition

Approach

Dry Run

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code