Inorder successor and predecessor in BST
Binary Search Trees
Medium
Medium
- Fun Fact: The problem of finding Inorder predecessor and successor in a Binary Search Tree (BST) can be seen in many real-world applications such as databases or software that deal with a large set of sorted data, allowing quick insertion, deletion and lookup operations
- For instance, popular database management systems like Oracle or MySQL use varieties of tree data structures such as B-Tree, B+ Tree (an extension of BST)
- When you need to find nearest lesser (predecessor) and nearest greater (successor) values to a particular key, applications can use Inorder traversal method, similar to the above mentioned problem, within such tree-based structures to get the result efficiently
- It's a common operation, particularly in navigating, organizing and managing hierarchical or ordered information
Given the root node of a binary search tree (BST) and an integer key. Return the Inorder predecessor and successor of the given key from the provided BST.
If predecessor or successor is missing then return -1.
Examples:
Input : root = [5, 2, 10, 1, 4, 7, 12] , key = 10
Output : [7, 12]
Explanation :
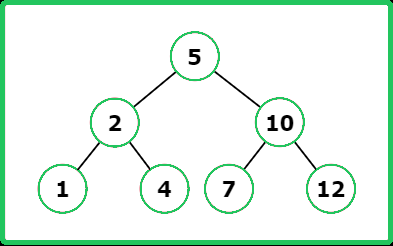
Input : root = [5, 2, 10, 1, 4, 7, 12] , key = 12
Output : [10, -1]
Explanation :
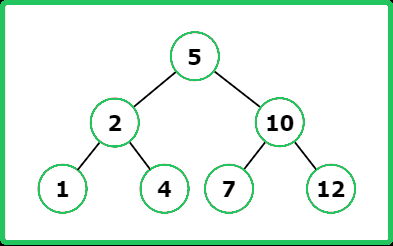
Input : root = [5, 2, 10, 1, 4, 7, 12] , key = 1
Constraints
- 1 <= Number of Nodes <= 104
- 1 <= Node.val <= 105
- All the values Node.val are unique.
Hints
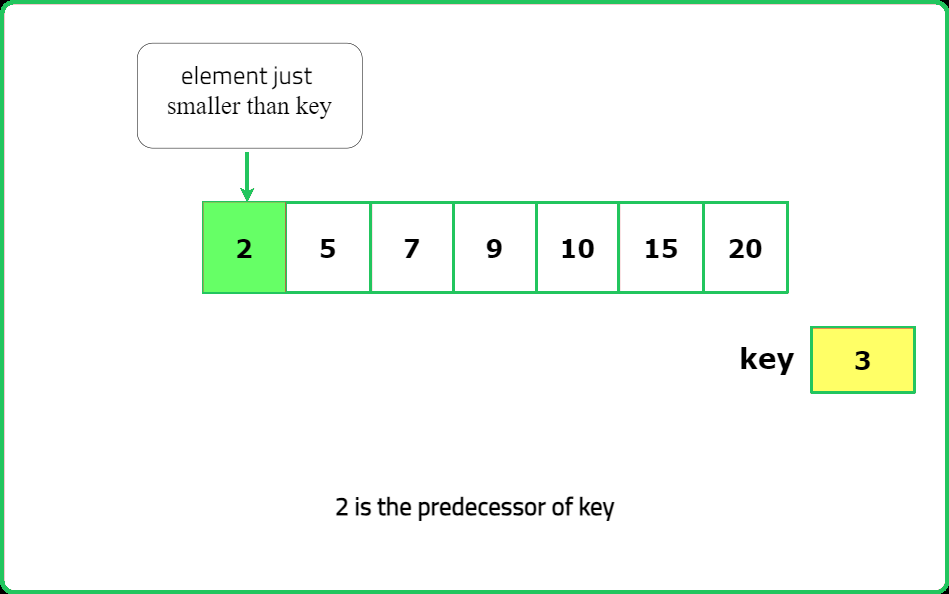
- "If key exists in the BST and has a left subtree, the predecessor is the rightmost (max) node in its left subtree. Otherwise, traverse the BST: If root.val < key, update predecessor = root.val and move right. Otherwise, move left."
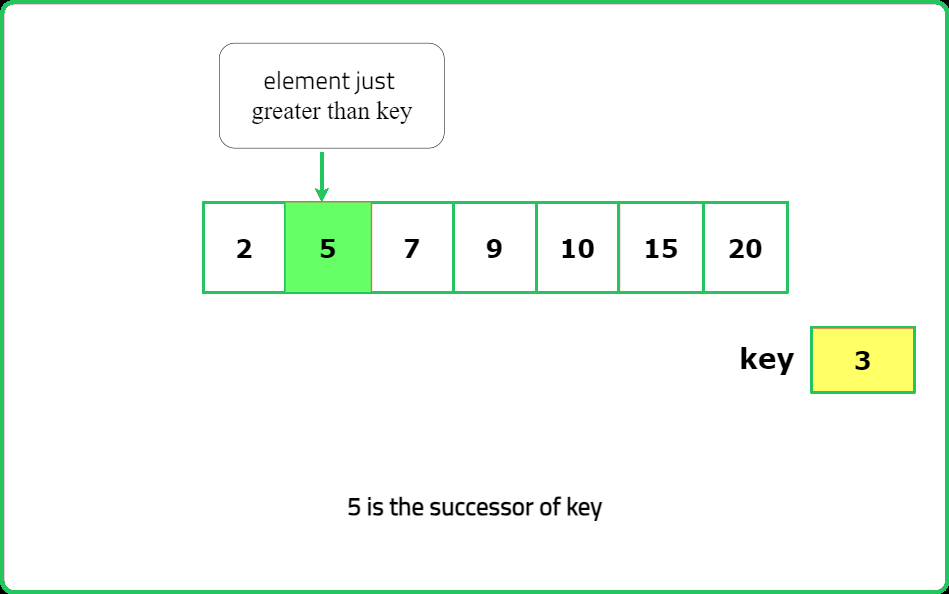
- "If key exists and has a right subtree, the successor is the leftmost (min) node in its right subtree. Otherwise, traverse the BST: If root.val > key, update successor = root.val and move left. Otherwise, move right."
Company Tags
Visa
Ernst & Young
Wayfair
Unity Technologies
Boston Consulting Group
Morgan Stanley
NVIDIA
Robinhood
Ubisoft
ARM
MongoDB
Alibaba
Epic Games
Electronic Arts
Philips Healthcare
Lyft
Qualcomm
OYO Rooms
HashiCorp
Deloitte
Teladoc Health
Bungie
Zynga
Snowflake
Salesforce
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition
To find the successor of a given node in a Binary Search Tree (BST), an efficient approach involves performing an in-order traversal of the tree. This traversal generates a sorted list of node values due to the inherent properties of BSTs. Once the sorted list is obtained, a binary search can be conducted on this list to identify the first value greater than the given key, which will be the successor. If the given key is the maximum value in the BST, it will be the last node in the in-order traversal, and hence, the successor does not exist.
Algorithm
- Traverse the BST in an in-order manner (Left, Root, Right).
- During the traversal, store each node's value in a list. This ensures that the list is sorted in ascending order.
- After completing the in-order traversal, the list will contain the BST's node values in sorted order.
- Perform a binary search on this sorted list to find the first value greater than the given key.
- If such a value is found, it is the successor of the given key. Return this value.
- If no such value exists (i.e., the key is the maximum value in the BST), return null.
Dry Run
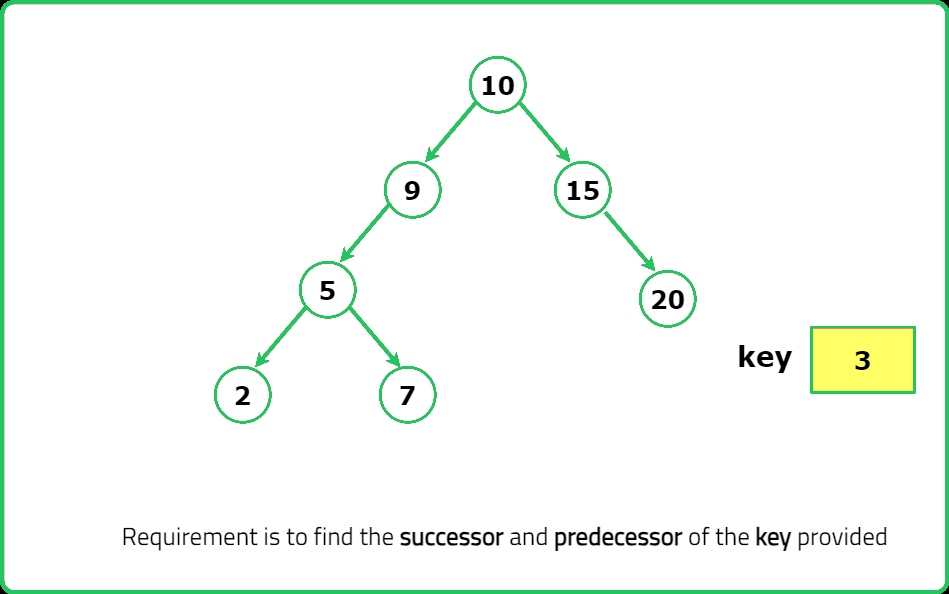
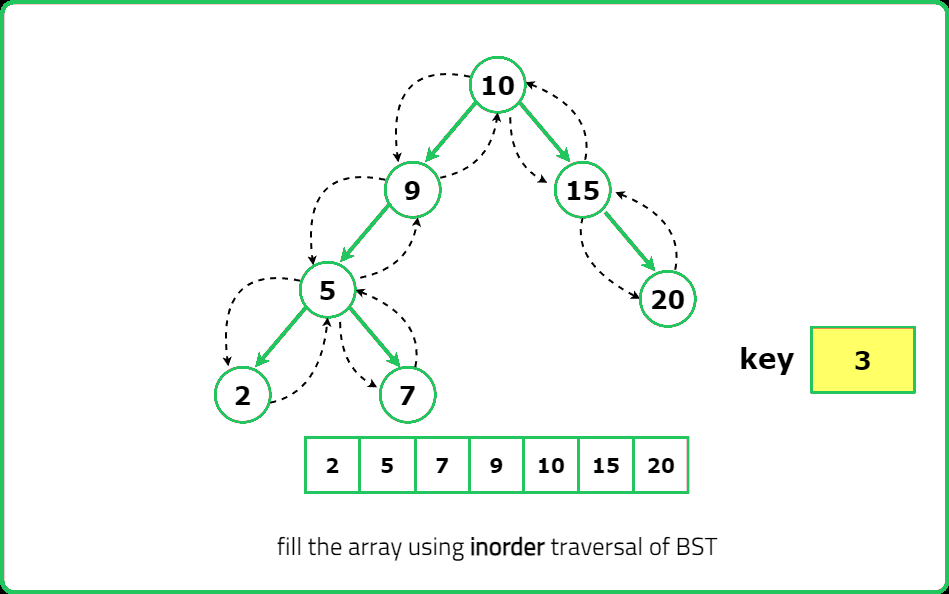
Solution
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
#include <bits/stdc++.h>
using namespace std;
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
// Constructor to initialize the node
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
vector<int> succPredBST(TreeNode* root, int key) {
vector<int> sortedList;
// Perform in-order traversal to get the sorted list of node values
inorderTraversal(root, sortedList);
int predecessor = -1;
int successor = -1;
// Find the predecessor and successor in the sorted list
for (int i = 0; i < sortedList.size(); i++) {
if (sortedList[i] < key) {
// Update predecessor if the current value is less than the key
predecessor = sortedList[i];
} else if (sortedList[i] > key) {
// Update successor if the current value is greater than the key
successor = sortedList[i];
break; // No need to continue once successor is found
}
}
return {predecessor, successor};
}
private:
// Helper function to perform in-order traversal
void inorderTraversal(TreeNode* node, vector<int>& sortedList) {
if (node == nullptr) {
return;
}
// Traverse the left subtree
inorderTraversal(node->left, sortedList);
// Add the node's value to the sortedList
sortedList.push_back(node->data);
// Traverse the right subtree
inorderTraversal(node->right, sortedList);
}
};
// Example usage
#include <iostream>
int main() {
// Create the BST
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(2);
root->right = new TreeNode(10);
root->left->left = new TreeNode(1);
root->left->right = new TreeNode(4);
root->right->left = new TreeNode(7);
root->right->right = new TreeNode(12);
// Create Solution object and get the predecessor and successor
Solution sol;
vector<int> result = sol.succPredBST(root, 10);
cout << "[" << result[0] << ", " << result[1] << "]" << endl; // Output: [7, 12]
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
import java.util.*;
public class TreeNode {
int data;
TreeNode left;
TreeNode right;
// Constructor to initialize the node
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
List<Integer> succPredBST(TreeNode root, int key) {
List<Integer> sortedList = new ArrayList<>();
// Perform in-order traversal to get the sorted list of node values
inorderTraversal(root, sortedList);
int predecessor = -1;
int successor = -1;
// Find the predecessor and successor in the sorted list
for (int i = 0; i < sortedList.size(); i++) {
if (sortedList.get(i) < key) {
// Update predecessor if the current value is less than the key
predecessor = sortedList.get(i);
} else if (sortedList.get(i) > key) {
// Update successor if the current value is greater than the key
successor = sortedList.get(i);
break; // No need to continue once successor is found
}
}
List<Integer> result = new ArrayList<>();
result.add(predecessor);
result.add(successor);
return result;
}
// Helper function to perform in-order traversal
private void inorderTraversal(TreeNode node, List<Integer> sortedList) {
if (node == null) {
return;
}
// Traverse the left subtree
inorderTraversal(node.left, sortedList);
// Add the node's value to the sortedList
sortedList.add(node.data);
// Traverse the right subtree
inorderTraversal(node.right, sortedList);
}
// Example usage
public static void main(String[] args) {
// Create the BST
TreeNode root = new TreeNode(5);
root.left = new TreeNode(2);
root.right = new TreeNode(10);
root.left.left = new TreeNode(1);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(7);
root.right.right = new TreeNode(12);
// Create Solution object and get the predecessor and successor
Solution sol = new Solution();
System.out.println(sol.succPredBST(root, 10)); // Output: [7, 12]
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
def succPredBST(self, root, key):
# Helper function to perform in-order traversal and collect node values
def inorder_traversal(node, sorted_list):
# Base case: if the node is None, return
if node is None:
return
# Traverse the left subtree
inorder_traversal(node.left, sorted_list)
# Add the node's value to the sorted_list
sorted_list.append(node.data)
# Traverse the right subtree
inorder_traversal(node.right, sorted_list)
sorted_list = []
# Perform in-order traversal to get the sorted list of node values
inorder_traversal(root, sorted_list)
# Initialize predecessor and successor
predecessor = -1
successor = -1
# Find the predecessor and successor in the sorted list
for i in range(len(sorted_list)):
if sorted_list[i] < key:
# Update predecessor if the current value is less than the key
predecessor = sorted_list[i]
elif sorted_list[i] > key:
# Update successor if the current value is greater than the key
successor = sorted_list[i]
break # No need to continue once successor is found
return [predecessor, successor]
# Example usage
if __name__ == "__main__":
# Create the BST
root = TreeNode(5)
root.left = TreeNode(2)
root.right = TreeNode(10)
root.left.left = TreeNode(1)
root.left.right = TreeNode(4)
root.right.left = TreeNode(7)
root.right.right = TreeNode(12)
# Create Solution object and get the predecessor and successor
sol = Solution()
print(sol.succPredBST(root, 10)) # Output: [7, 12]
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null){
* this.data = val;
* this.left = left;
* this.right = right;
* }
* }
**/
class Solution {
succPredBST(root, key) {
// Helper function to perform in-order traversal and collect node values
const inorderTraversal = (node, sortedList) => {
if (node === null) return;
// Traverse the left subtree
inorderTraversal(node.left, sortedList);
// Add the node's value to the sortedList
sortedList.push(node.data);
// Traverse the right subtree
inorderTraversal(node.right, sortedList);
};
let sortedList = [];
// Perform in-order traversal to get the sorted list of node values
inorderTraversal(root, sortedList);
// Initialize predecessor and successor
let predecessor = -1;
let successor = -1;
// Find the predecessor and successor in the sorted list
for (let i = 0; i < sortedList.length; i++) {
if (sortedList[i] < key) {
// Update predecessor if the current value is less than the key
predecessor = sortedList[i];
} else if (sortedList[i] > key) {
// Update successor if the current value is greater than the key
successor = sortedList[i];
break; // No need to continue once successor is found
}
}
return [predecessor, successor];
}
}
// Example usage
const root = new TreeNode(5);
root.left = new TreeNode(2);
root.right = new TreeNode(10);
root.left.left = new TreeNode(1);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(7);
root.right.right = new TreeNode(12);
const sol = new Solution();
console.log(sol.succPredBST(root, 10)); // Output: [7, 12]
Complexity Analysis
Time Complexity : O(N), where N is the number of nodes in the binary search tree. The inorder traversal visits each node once, and the subsequent for loop also iterates over the nodes.
Space Complexity : O(N), where N is the number of nodes in the binary search tree. The sortedList array stores all the node values, resulting in a linear space complexity.
Intuition
An optimized approach to finding the inorder successor in a Binary Search Tree (BST) involves performing an inorder traversal while keeping track of the first node with a value greater than the given key. The properties of BSTs ensure that an inorder traversal yields node values in ascending order, making it straightforward to identify the next node value following a given key. This method leverages the structure of BSTs to efficiently determine the inorder successor without requiring additional data structures.
Algorithm
- Begin by performing an inorder traversal of the Binary Search Tree (BST), which can be done using traditional methods or the Morris Inorder Traversal technique for optimized space complexity.
- During the traversal, continuously monitor each node, and identify the first node whose value is greater than the specified key.
- The node identified in the previous step is the inorder successor of the given key. Once this node is found, return it as the result.
Dry Run
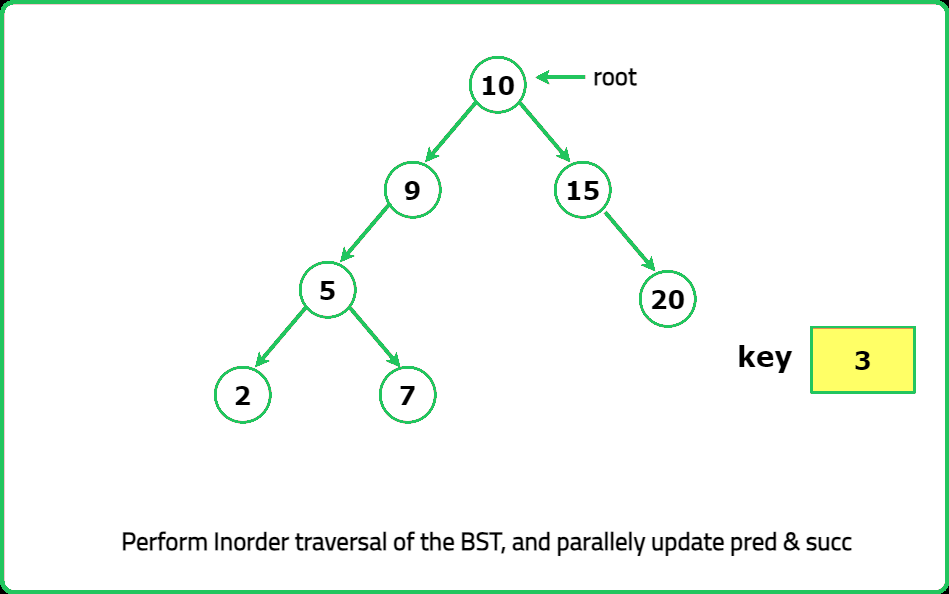
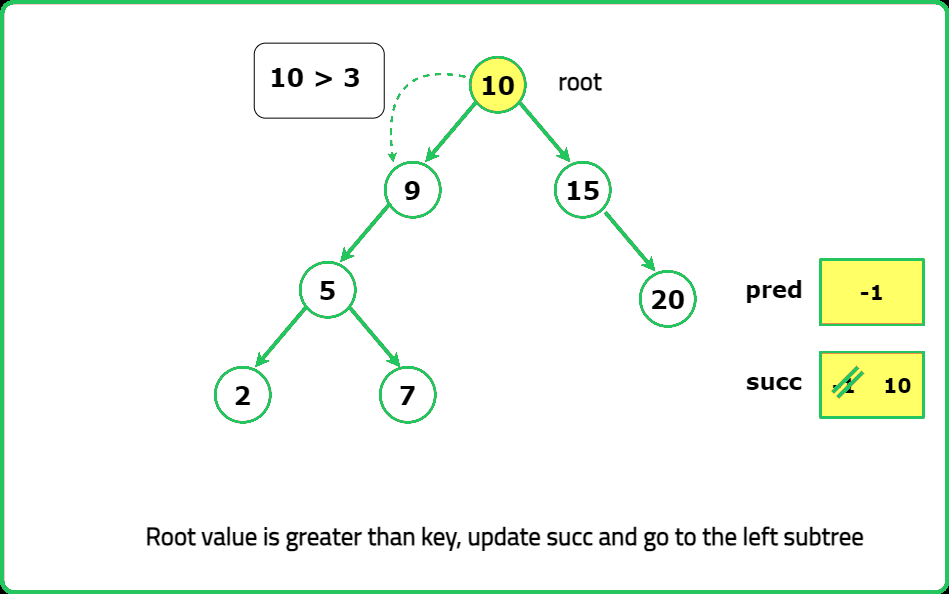
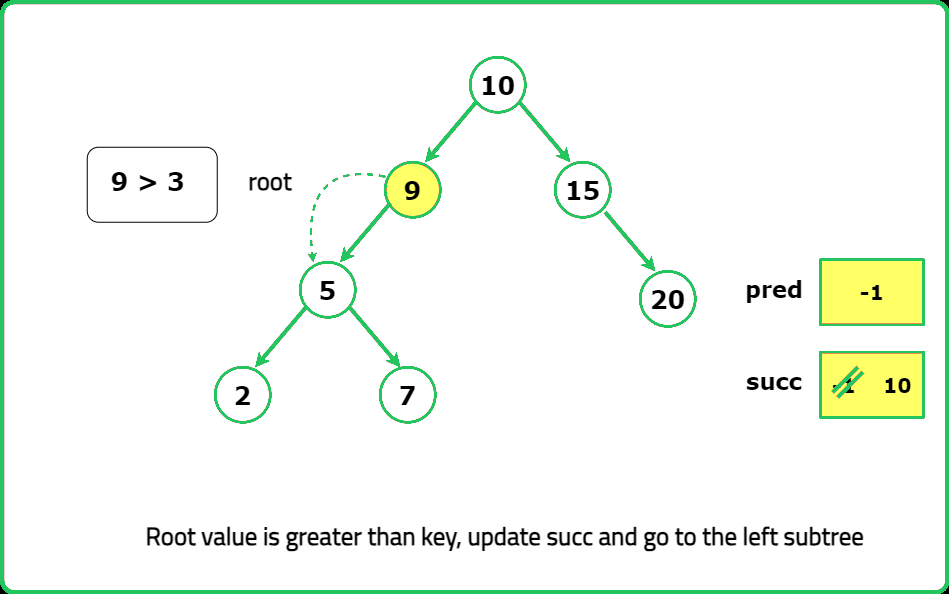
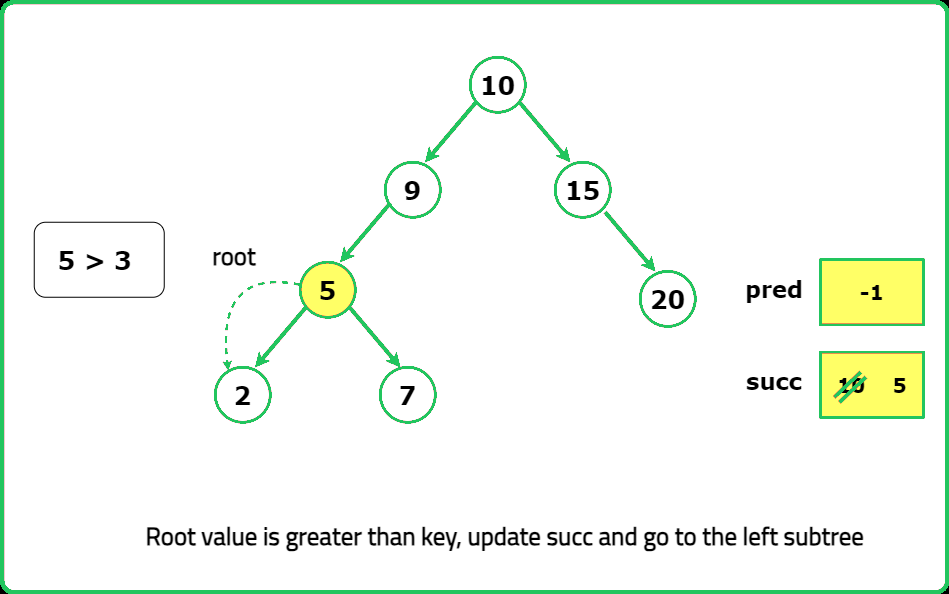
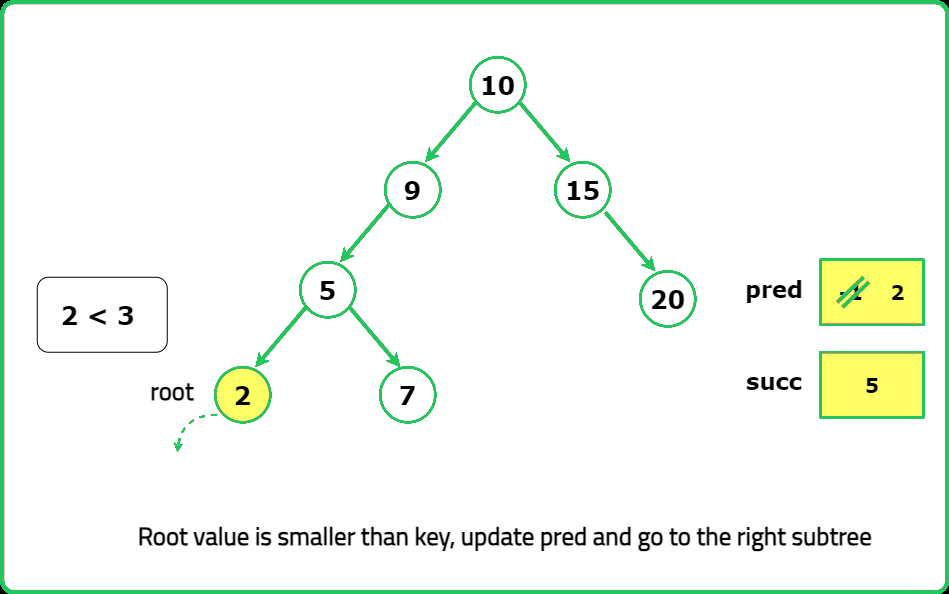
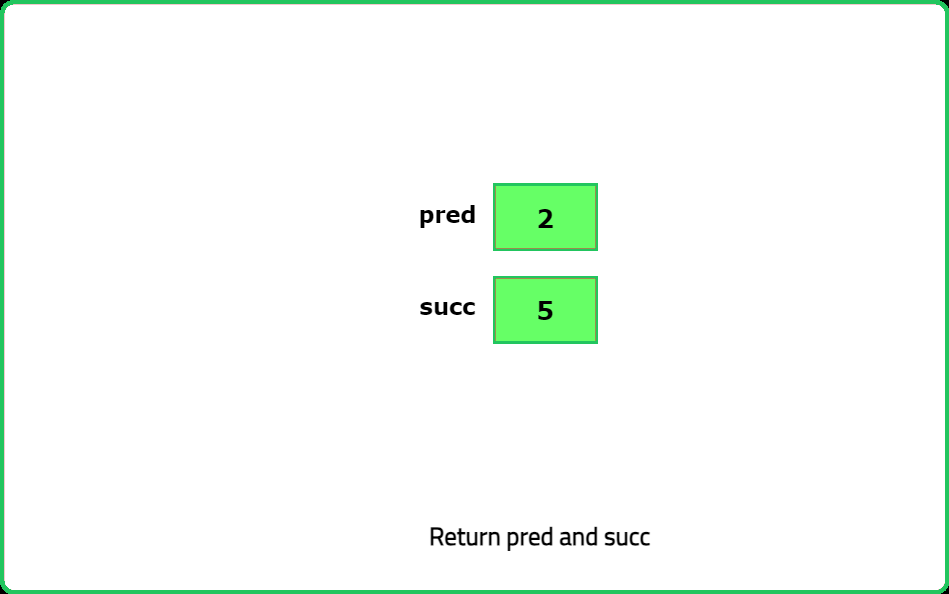
Solution
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091
#include <bits/stdc++.h>
using namespace std;
// Definition for a binary tree node
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : data(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
vector<int> succPredBST(TreeNode* root, int key) {
vector<int> result;
TreeNode* succ = nullptr;
TreeNode* pred = nullptr;
while (root != nullptr) {
if (root->data == key) {
// If the key is found, find the predecessor and successor
if (root->right != nullptr) {
succ = findMin(root->right);
}
if (root->left != nullptr) {
pred = findMax(root->left);
}
break;
} else if (root->data < key) {
// If current node's value is less than key, move to the right subtree
pred = root;
root = root->right;
} else {
// If current node's value is greater than key, move to the left subtree
succ = root;
root = root->left;
}
}
if (pred != nullptr) {
result.push_back(pred->data);
} else {
result.push_back(-1); // or handle differently if predecessor not found
}
if (succ != nullptr) {
result.push_back(succ->data);
} else {
result.push_back(-1); // or handle differently if successor not found
}
return result;
}
private:
// Helper function to find the minimum value node in a subtree
TreeNode* findMin(TreeNode* node) {
while (node->left != nullptr) {
node = node->left;
}
return node;
}
// Helper function to find the maximum value node in a subtree
TreeNode* findMax(TreeNode* node) {
while (node->right != nullptr) {
node = node->right;
}
return node;
}
};
int main() {
// Example usage
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(3);
root->right = new TreeNode(8);
root->left->left = new TreeNode(2);
root->left->right = new TreeNode(4);
root->right->left = new TreeNode(6);
root->right->right = new TreeNode(9);
Solution sol;
vector<int> result = sol.succPredBST(root, 4);
cout << "Predecessor: " << result[0] << ", Successor: " << result[1] << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091
import java.util.ArrayList;
import java.util.List;
// Definition for a binary tree node
class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int x) {
data = x;
}
}
public class Main {
public static void main(String[] args) {
// Example usage
TreeNode root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(8);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(9);
Solution sol = new Solution();
List<Integer> result = sol.succPredBST(root, 4);
System.out.println("Predecessor: " + result.get(0) + ", Successor: " + result.get(1));
}
}
class Solution {
public List<Integer> succPredBST(TreeNode root, int key) {
List<Integer> result = new ArrayList<>();
TreeNode succ = null;
TreeNode pred = null;
while (root != null) {
if (root.data == key) {
// If the key is found, find the predecessor and successor
if (root.right != null) {
succ = findMin(root.right);
}
if (root.left != null) {
pred = findMax(root.left);
}
break;
} else if (root.data < key) {
// If current node's value is less than key, move to the right subtree
pred = root;
root = root.right;
} else {
// If current node's value is greater than key, move to the left subtree
succ = root;
root = root.left;
}
}
if (pred != null) {
result.add(pred.data);
} else {
result.add(-1); // or handle differently if predecessor not found
}
if (succ != null) {
result.add(succ.data);
} else {
result.add(-1); // or handle differently if successor not found
}
return result;
}
// Helper function to find the minimum value node in a subtree
private TreeNode findMin(TreeNode node) {
while (node.left != null) {
node = node.left;
}
return node;
}
// Helper function to find the maximum value node in a subtree
private TreeNode findMax(TreeNode node) {
while (node.right != null) {
node = node.right;
}
return node;
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869
# Definition for a binary tree node
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Solution:
def succPredBST(self, root: TreeNode, key: int) -> list:
result = []
succ = None
pred = None
while root:
if root.data == key:
# If the key is found, find the predecessor and successor
if root.right:
succ = self.findMin(root.right)
if root.left:
pred = self.findMax(root.left)
break
elif root.data < key:
# If current node's value is less than key, move to the right subtree
pred = root
root = root.right
else:
# If current node's value is greater than key, move to the left subtree
succ = root
root = root.left
if pred:
result.append(pred.data)
else:
result.append(-1) # or handle differently if predecessor not found
if succ:
result.append(succ.data)
else:
result.append(-1) # or handle differently if successor not found
return result
# Helper function to find the minimum value node in a subtree
def findMin(self, node: TreeNode) -> TreeNode:
while node.left:
node = node.left
return node
# Helper function to find the maximum value node in a subtree
def findMax(self, node: TreeNode) -> TreeNode:
while node.right:
node = node.right
return node
# Example usage
if __name__ == "__main__":
# Example tree construction
root = TreeNode(5)
root.left = TreeNode(3)
root.right = TreeNode(8)
root.left.left = TreeNode(2)
root.left.right = TreeNode(4)
root.right.left = TreeNode(6)
root.right.right = TreeNode(9)
sol = Solution()
result = sol.succPredBST(root, 4)
print(f"Predecessor: {result[0]}, Successor: {result[1]}")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081
// Definition for a binary tree node
class TreeNode {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class Solution {
succPredBST(root, key) {
let result = [];
let succ = null;
let pred = null;
while (root !== null) {
if (root.data === key) {
// If the key is found, find the predecessor and successor
if (root.right !== null) {
succ = this.findMin(root.right);
}
if (root.left !== null) {
pred = this.findMax(root.left);
}
break;
} else if (root.data < key) {
// If current node's value is less than key, move to the right subtree
pred = root;
root = root.right;
} else {
// If current node's value is greater than key, move to the left subtree
succ = root;
root = root.left;
}
}
if (pred !== null) {
result.push(pred.data);
} else {
result.push(-1); // or handle differently if predecessor not found
}
if (succ !== null) {
result.push(succ.data);
} else {
result.push(-1); // or handle differently if successor not found
}
return result;
}
// Helper function to find the minimum value node in a subtree
findMin(node) {
while (node.left !== null) {
node = node.left;
}
return node;
}
// Helper function to find the maximum value node in a subtree
findMax(node) {
while (node.right !== null) {
node = node.right;
}
return node;
}
}
// Example usage
let root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(8);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(9);
let sol = new Solution();
let result = sol.succPredBST(root, 4);
console.log(`Predecessor: ${result[0]}, Successor: ${result[1]}`);
Complexity Analysis
Time Complexity : O(H), explanation in few words: where H is the height of the BST.
Space Complexity : O(1), explanation in few words: since only a constant amount of space is used.
Intuition
This approach takes advantage of the unique properties of a Binary Search Tree (BST) to efficiently find an element's successor. The BST's structure allows quick navigation based on node values. To find the successor of a given node, a variable 'successor' is initialized to null. As the tree is traversed, any value greater than the given key is tracked. When such a value is found, 'successor' is updated to be the smaller of the current 'successor' and the newly encountered value.
Algorithm
- Initialize a variable 'successor' to a very high value (e.g., the maximum integer value).
- Traverse the BST
- Start at the root of the BST and compare the key with the current node's value.
- If the current node's value is smaller than the key, move to the right child because the successor must be in the right subtree.
- If the current node's value is greater than the key, update 'successor' to be the smaller value between the current 'successor' and the current node's value, then move to the left child because the successor could be in the left subtree.
- Repeat the above steps until reaching a null node. At the end of the traversal, 'successor' will hold the value of the inorder successor of the given key if it exists; otherwise, it remains as the initial very high value.
- Check if 'successor' is still the initial high value. If it is, return null (indicating no successor exists). Otherwise, return 'successor'.
Dry Run
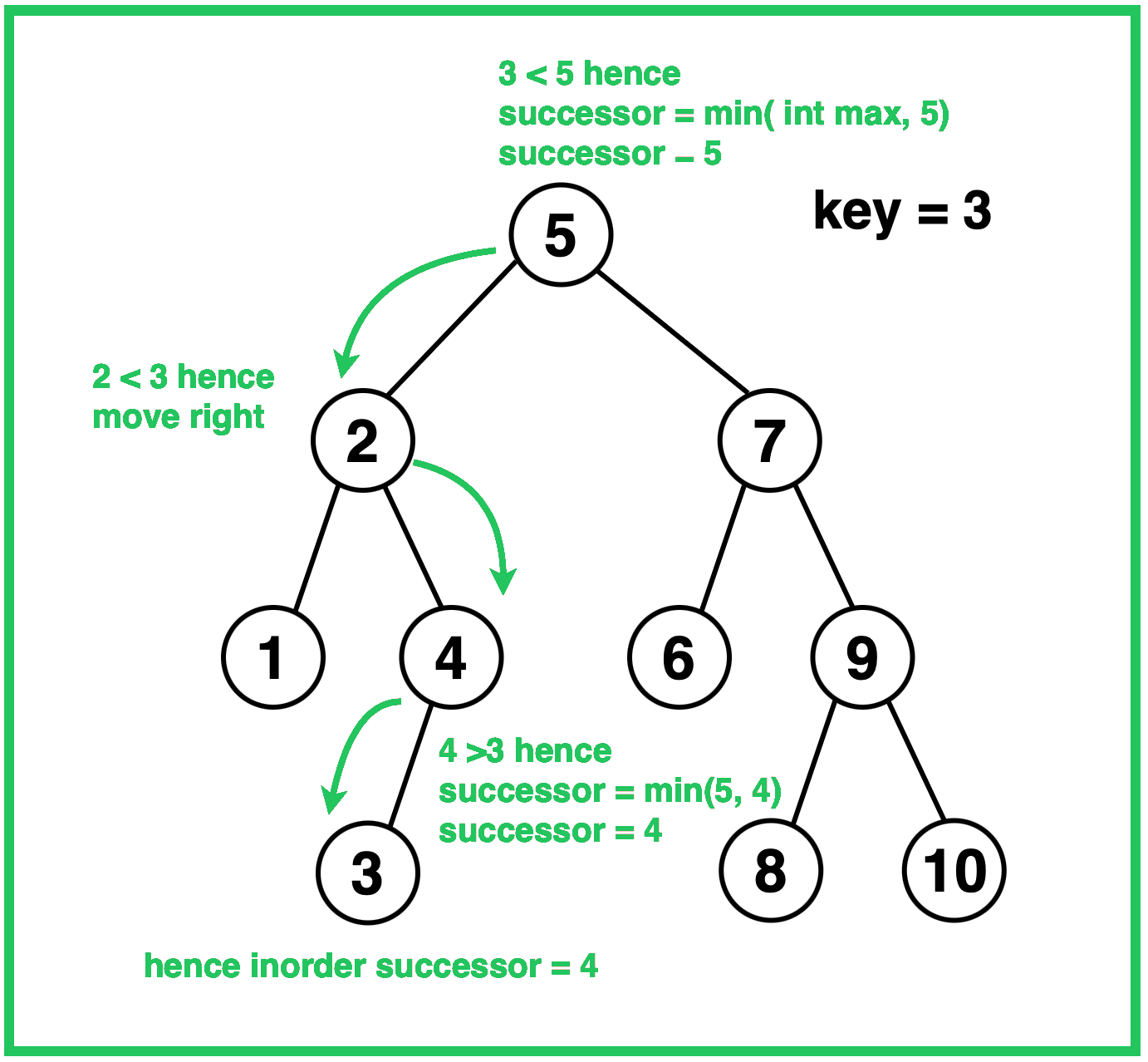
Solution
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081
#include <bits/stdc++.h>
using namespace std;
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
vector< int > succPredBST(TreeNode* root, int key) {
int predecessor = -1;
int successor = numeric_limits< int >::max();
// Lambda function to traverse the tree and find successor and predecessor
function< void(TreeNode*) > traverse = [&](TreeNode* node) {
if (node == nullptr) {
return;
}
if (node->data < key) {
// Update predecessor and move to the right subtree
predecessor = max(predecessor, node->data);
traverse(node->right);
} else if (node->data > key) {
// Update successor and move to the left subtree
successor = min(successor, node->data);
traverse(node->left);
} else {
// If node's value equals key, find predecessor and successor in subtrees
if (node->left != nullptr) {
// Find maximum value in left subtree for predecessor
TreeNode* temp = node->left;
while (temp->right != nullptr) {
temp = temp->right;
}
predecessor = temp->data;
}
if (node->right != nullptr) {
// Find minimum value in right subtree for successor
TreeNode* temp = node->right;
while (temp->left != nullptr) {
temp = temp->left;
}
successor = temp->data;
}
}
};
traverse(root);
// Return the result as a vector with predecessor and successor
return {
predecessor == -1 ? -1 : predecessor,
successor == numeric_limits< int >::max() ? -1 : successor
};
}
};
// Example usage
#include <iostream>
int main() {
// Create the BST
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(2);
root->right = new TreeNode(10);
root->left->left = new TreeNode(1);
root->left->right = new TreeNode(4);
root->right->left = new TreeNode(7);
root->right->right = new TreeNode(12);
// Create Solution object and get the predecessor and successor
Solution sol;
vector<int> result = sol.succPredBST(root, 10);
cout << "[" << result[0] << ", " << result[1] << "]" << endl; // Output: [7, 12]
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879
import java.util.*;
class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
private static final int MAX_VALUE = Integer.MAX_VALUE;
// Instance variables to store predecessor and successor
private int predecessor = -1;
private int successor = MAX_VALUE;
// Function to find successor and predecessor in BST
public List < Integer > succPredBST(TreeNode root, int key) {
// Helper function to traverse the tree and find successor and predecessor
traverse(root, key);
// Return the result as a list with predecessor and successor
return Arrays.asList(predecessor == -1 ? -1 : predecessor, successor == MAX_VALUE ? -1 : successor);
}
// Method to traverse the tree
private void traverse(TreeNode node, int key) {
if (node == null) {
return;
}
if (node.data < key) {
// Update predecessor and move to the right subtree
predecessor = Math.max(predecessor, node.data);
traverse(node.right, key);
} else if (node.data > key) {
// Update successor and move to the left subtree
successor = Math.min(successor, node.data);
traverse(node.left, key);
} else {
// If node's value equals key, find predecessor and successor in subtrees
if (node.left != null) {
// Find maximum value in left subtree for predecessor
TreeNode temp = node.left;
while (temp.right != null) {
temp = temp.right;
}
predecessor = temp.data;
}
if (node.right != null) {
// Find minimum value in right subtree for successor
TreeNode temp = node.right;
while (temp.left != null) {
temp = temp.left;
}
successor = temp.data;
}
}
}
// Example usage
public static void main(String[] args) {
Solution solution = new Solution();
// Creating a simple BST for testing
TreeNode root = new TreeNode(20);
root.left = new TreeNode(10);
root.right = new TreeNode(30);
root.left.left = new TreeNode(5);
root.left.right = new TreeNode(15);
root.right.left = new TreeNode(25);
root.right.right = new TreeNode(35);
int key = 15;
List < Integer > result = solution.succPredBST(root, key);
// Output the result
System.out.println("Predecessor: " + result.get(0) + ", Successor: " + result.get(1));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
import sys
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
def succPredBST(self, root, key):
# Initialize predecessor and successor to special values
predecessor = -1
successor = sys.maxsize
# Helper function to traverse the tree and find the successor and predecessor
def traverse(node):
nonlocal predecessor, successor
if node is None:
return
if node.data < key:
# If node's value is less than key, update predecessor
predecessor = max(predecessor, node.data)
# Continue to right subtree
traverse(node.right)
elif node.data > key:
# If node's value is greater than key, update successor
successor = min(successor, node.data)
# Continue to left subtree
traverse(node.left)
else:
# If node's value is equal to key, find predecessor and successor in subtrees
if node.left:
# Find maximum value in the left subtree for predecessor
temp = node.left
while temp.right:
temp = temp.right
predecessor = temp.data
if node.right:
# Find minimum value in the right subtree for successor
temp = node.right
while temp.left:
temp = temp.left
successor = temp.data
traverse(root)
# Return the result as a list with predecessor and successor
# If successor or predecessor is unchanged, it means it was not found
return [predecessor if predecessor != -1 else -1, successor if successor != sys.maxsize else -1]
# Example usage
if __name__ == "__main__":
# Create the BST
root = TreeNode(5)
root.left = TreeNode(2)
root.right = TreeNode(10)
root.left.left = TreeNode(1)
root.left.right = TreeNode(4)
root.right.left = TreeNode(7)
root.right.right = TreeNode(12)
# Create Solution object and get the predecessor and successor
sol = Solution()
print(sol.succPredBST(root, 10)) # Output: [7, 12]
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null){
* this.data = val;
* this.left = left;
* this.right = right;
* }
* }
**/
class Solution {
succPredBST(root, key) {
// Initialize predecessor and successor to special values
let predecessor = -1;
let successor = Number.MAX_SAFE_INTEGER;
// Helper function to traverse the tree and find successor and predecessor
const traverse = (node) => {
if (node === null) return;
if (node.data < key) {
// Update predecessor and move to the right subtree
predecessor = Math.max(predecessor, node.data);
traverse(node.right);
} else if (node.data > key) {
// Update successor and move to the left subtree
successor = Math.min(successor, node.data);
traverse(node.left);
} else {
// If node's value equals key, find predecessor and successor in subtrees
if (node.left !== null) {
// Find maximum value in left subtree for predecessor
let temp = node.left;
while (temp.right !== null) {
temp = temp.right;
}
predecessor = temp.data;
}
if (node.right !== null) {
// Find minimum value in right subtree for successor
let temp = node.right;
while (temp.left !== null) {
temp = temp.left;
}
successor = temp.data;
}
}
};
traverse(root);
// Return the result as an array with predecessor and successor
return [predecessor === -1 ? -1 : predecessor, successor === Number.MAX_SAFE_INTEGER ? -1 : successor];
}
}
// Example usage
const root = new TreeNode(5);
root.left = new TreeNode(2);
root.right = new TreeNode(10);
root.left.left = new TreeNode(1);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(7);
root.right.right = new TreeNode(12);
const sol = new Solution();
console.log(sol.succPredBST(root, 10)); // Output: [7, 12]
Complexity Analysis
Time Complexity : O(N), traversing the binary tree once where N is the number of nodes.
Space Complexity : O(1), using a constant amount of space to store the predecessor, successor, and temporary variables.
Frequently Occurring Doubts
Q: Why do we move left for the successor and right for the predecessor?
A: Because in a BST: Left subtree contains smaller values → Candidate for predecessor. Right subtree contains larger values → Candidate for successor.
Q: Can this problem be solved using inorder traversal?
A: Yes, but it takes O(n) time, while BST traversal is O(h) (log n for balanced BSTs).
Interview Followup Questions
Q: How would you modify this solution for a general Binary Tree (not BST)?
A: Perform inorder traversal and track predecessor and successor manually.
Q: How does this problem relate to binary search?
A: The approach mimics binary search, as we narrow down the predecessor and successor
Notes
Code
✅ Testcase
Input: {'key': '10', 'root': '5 2 10 1 4 7 12'}
Expected:
7 12
7 12
Actual: -
Time: -
sec
Status: Waiting
Input: {'key': '12', 'root': '5 2 10 1 4 7 12'}
Expected:
10 -1
10 -1
Actual: -
Time: -
sec
Status: Waiting
Input: {'key': '5', 'root': '4 1 12 null null 5 15'}
Expected:
4 12
4 12
Actual: -
Time: -
sec
Status: Waiting