Traversal Techniques
Graphs
Theory and traversals
Medium
Given an undirected connected graph with V vertices numbered from 0 to V-1, the task is to implement both Depth First Search (DFS) and Breadth First Search (BFS) traversals starting from the 0th vertex. The graph is represented using an adjacency list where adj[i] contains a list of vertices connected to vertex i. Visit nodes in the order they appear in the adjacency list.
Examples:
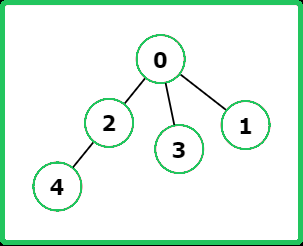
Input: V = 5, adj = [[2, 3, 1], [0], [0, 4], [0], [2]]
Output:[0, 2, 4, 3, 1], [0, 2, 3, 1, 4]
Explanation:
DFS: Start from vertex 0. Visit vertex 2, then vertex 4, backtrack to vertex 0, then visit vertex 3, and finally vertex 1. The traversal is 0 → 2 → 4 → 3 → 1.
BFS: Start from vertex 0. Visit vertices 2, 3, and 1 (in the order they appear in the adjacency list). Then, visit vertex 4 from vertex 2. The traversal is 0 → 2 → 3 → 1 → 4.
Input: V = 4, adj = [[1, 3], [2, 0], [1], [0]]
Output: [0, 1, 2, 3], [0, 1, 3, 2]
Explanation:
DFS: Start from vertex 0. Visit vertex 1, then vertex 2, backtrack to vertex 0, then visit vertex 3. The traversal is 0 → 1 → 2 → 3.
BFS: Start from vertex 0. Visit vertices 1 and 3, then visit vertex 2 from vertex 1. The traversal is 0 → 1 → 3 → 2.
Input: V = 3, adj = [[1, 2], [0], [0]]
Constraints
- E= Number of Edges
- 1 ≤ V, E ≤ 104
Hints
- "Use recursion (or a stack) to explore as deep as possible before backtracking. Maintain a visited array to mark visited nodes and avoid cycles. Start from vertex 0 and visit nodes in the order they appear in adj[i]."
- "Use a queue to explore nodes level by level (FIFO order). Begin from 0, mark it as visited, and process all connected nodes before moving deeper. The traversal order follows the order of neighbors in adj[i]."
Company Tags
Oracle
Intel
Twilio
Swiggy
MongoDB
JPMorgan Chase
Alibaba
Broadcom
Shopify
Boston Consulting Group
Cloudflare
Target
Etsy
Unity Technologies
Stripe
Roche
Johnson & Johnson
Dropbox
Splunk
Qualcomm
ARM
Epic Systems
Lyft
Western Digital
Deloitte
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
The traversal techniques form the basics of any graph problem. One of the two traversal techniques is Breadth First Search(BFS), also known as Level Order Traversal. Breadth-First Search (BFS) is a traversal technique that explores all the neighbors of a node before moving to the next level of neighbors. It uses a queue data structure.
Approach:
- Mark all nodes as unvisited. Create an empty queue.
- Enqueue the source node. Mark the source node as visited.
- While the queue is not empty:
- Dequeue the front node. Process the node.
- For each adjacent unvisited node, enqueue the adjacent node and mark it as visited.
- Repeat the process until all nodes are visited.
---!>
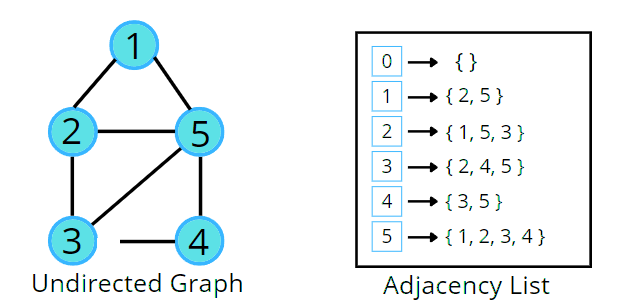
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Helper function to perform BFS
traversal from the node */
void bfs(int node, vector<int> adj[], int vis[],
vector<int> &ans) {
// Queue data structure
queue<int> q;
// Push the starting node
q.push(node);
// Until the queue is empty
while(!q.empty()) {
// Get the node
int node = q.front();
q.pop();
// Add the node to answer
ans.push_back(node);
// Traverse for all its neighbours
for(auto it : adj[node]) {
/* If the neighbour has previously not been
visited, store in Q and mark as visited */
if(!vis[it]) {
vis[it] = 1;
q.push(it);
}
}
}
// Return
return;
}
/* Helper function to recursively
perform DFS from the node */
void dfs(int node, vector<int> adj[], int vis[],
vector<int> &ans) {
// Mark the node as visited
vis[node] = 1;
// Add the node to the result
ans.push_back(node);
// Traverse all its neighbours
for(auto it : adj[node]) {
// If the neighbour is not visited
if(!vis[it]) {
// Perform DFS recursively
dfs(it, adj, vis, ans);
}
}
}
public:
/* Function to return a list containing
the DFS traversal of the graph */
vector<int> dfsOfGraph(int V, vector<int> adj[]) {
// Visited array
int vis[V] = {0};
// Create a list to store DFS
vector<int> ans;
// Traverse all the nodes
for(int i=0; i < V; i++) {
// If the node is unvisited
if(vis[i] == 0) {
// Call DFS from that node
dfs(i, adj, vis, ans);
}
}
// Return the result
return ans;
}
/* Function to return a list containing
the BFS traversal of the graph */
vector<int> bfsOfGraph(int V, vector<int> adj[]) {
// Visited array
int vis[V] = {0};
// To store the result
vector<int> ans;
// Traverse all the nodes
for(int i=0; i < V; i++) {
// If the node is unvisited
if(vis[i] == 0) {
// Mark the node as visited
vis[i] = 1;
// Call BFS from that node
bfs(i, adj, vis, ans);
}
}
return ans;
}
};
int main() {
int V = 5;
vector<int> adj[] = {
{2, 3, 1},
{0},
{0, 4},
{0},
{2}
};
// Creating instance of Solution class
Solution sol;
// Function call to get the BFS traversal of graph
vector<int> bfs = sol.bfsOfGraph(V, adj);
// Function call to get the BFS traversal of graph
vector<int> dfs = sol.dfsOfGraph(V, adj);
// Output
cout << "The BFS traversal of the given graph is: ";
for(int i=0; i < bfs.size(); i++) {
cout << bfs[i] << " ";
}
cout << "\nThe DFS traversal of the given graph is: ";
for(int i=0; i < dfs.size(); i++) {
cout << dfs[i] << " ";
}
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
import java.util.*;
class Solution {
/* Helper function to perform BFS
traversal from the node */
private void bfs(int node, List<Integer>[] adj, boolean[] vis,
List<Integer> ans) {
// Queue data structure
Queue<Integer> q = new LinkedList<>();
// Push the starting node
q.add(node);
// Until the queue is empty
while (!q.isEmpty()) {
// Get the node
int current = q.poll();
// Add the node to answer
ans.add(current);
// Traverse for all its neighbours
for (int it : adj[current]) {
/* If the neighbour has previously not been
visited, store in Q and mark as visited */
if (!vis[it]) {
vis[it] = true;
q.add(it);
}
}
}
}
/* Helper function to recursively
perform DFS from the node */
private void dfs(int node, List<Integer>[] adj, boolean[] vis,
List<Integer> ans) {
// Mark the node as visited
vis[node] = true;
// Add the node to the result
ans.add(node);
// Traverse all its neighbours
for (int it : adj[node]) {
// If the neighbour is not visited
if (!vis[it]) {
// Perform DFS recursively
dfs(it, adj, vis, ans);
}
}
}
/* Function to return a list containing
the DFS traversal of the graph */
public List<Integer> dfsOfGraph(int V, List<Integer>[] adj) {
// Visited array
boolean[] vis = new boolean[V];
// Create a list to store DFS
List<Integer> ans = new ArrayList<>();
// Traverse all the nodes
for (int i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Call DFS from that node
dfs(i, adj, vis, ans);
}
}
// Return the result
return ans;
}
/* Function to return a list containing
the BFS traversal of the graph */
public List<Integer> bfsOfGraph(int V, List<Integer>[] adj) {
// Visited array
boolean[] vis = new boolean[V];
// To store the result
List<Integer> ans = new ArrayList<>();
// Traverse all the nodes
for (int i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Mark the node as visited
vis[i] = true;
// Call BFS from that node
bfs(i, adj, vis, ans);
}
}
return ans;
}
public static void main(String[] args) {
int V = 5;
List<Integer>[] adj = new List[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
adj[0].addAll(Arrays.asList(2, 3, 1));
adj[1].add(0);
adj[2].addAll(Arrays.asList(0, 4));
adj[3].add(0);
adj[4].add(2);
// Creating instance of Solution class
Solution sol = new Solution();
// Function call to get the BFS traversal of graph
List<Integer> bfs = sol.bfsOfGraph(V, adj);
// Function call to get the DFS traversal of graph
List<Integer> dfs = sol.dfsOfGraph(V, adj);
// Output
System.out.println("The BFS traversal of the given graph is: " + bfs);
System.out.println("The DFS traversal of the given graph is: " + dfs);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109
from collections import deque
class Solution:
# Helper function to perform BFS
# traversal from the node
def bfs(self, node, adj, vis, ans):
# Queue data structure
q = deque()
# Push the starting node
q.append(node)
# Until the queue is empty
while q:
# Get the node
node = q.popleft()
# Add the node to answer
ans.append(node)
# Traverse for all its neighbours
for it in adj[node]:
# If the neighbour has previously not been
# visited, store in Q and mark as visited
if not vis[it]:
vis[it] = 1
q.append(it)
# Helper function to recursively
# perform DFS from the node
def dfs(self, node, adj, vis, ans):
# Mark the node as visited
vis[node] = 1
# Add the node to the result
ans.append(node)
# Traverse all its neighbours
for it in adj[node]:
# If the neighbour is not visited
if not vis[it]:
# Perform DFS recursively
self.dfs(it, adj, vis, ans)
# Function to return a list containing
# the DFS traversal of the graph
def dfsOfGraph(self, V, adj):
# Visited array
vis = [0] * V
# Create a list to store DFS
ans = []
# Traverse all the nodes
for i in range(V):
# If the node is unvisited
if vis[i] == 0:
# Call DFS from that node
self.dfs(i, adj, vis, ans)
# Return the result
return ans
# Function to return a list containing
# the BFS traversal of the graph
def bfsOfGraph(self, V, adj):
# Visited array
vis = [0] * V
# To store the result
ans = []
# Traverse all the nodes
for i in range(V):
# If the node is unvisited
if vis[i] == 0:
# Mark the node as visited
vis[i] = 1
# Call BFS from that node
self.bfs(i, adj, vis, ans)
return ans
if __name__ == "__main__":
V = 5
adj = [
[2, 3, 1],
[0],
[0, 4],
[0],
[2]
]
# Creating instance of Solution class
sol = Solution()
# Function call to get the BFS traversal of graph
bfs = sol.bfsOfGraph(V, adj)
# Function call to get the DFS traversal of graph
dfs = sol.dfsOfGraph(V, adj)
# Output
print("The BFS traversal of the given graph is: ", bfs)
print("The DFS traversal of the given graph is: ", dfs)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123
class Solution {
/* Helper function to perform BFS
traversal from the node */
bfs(node, adj, vis, ans) {
// Queue data structure
const q = [];
// Push the starting node
q.push(node);
// Until the queue is empty
while (q.length > 0) {
// Get the node
const current = q.shift();
// Add the node to answer
ans.push(current);
// Traverse for all its neighbours
for (const it of adj[current]) {
/* If the neighbour has previously not been
visited, store in Q and mark as visited */
if (!vis[it]) {
vis[it] = true;
q.push(it);
}
}
}
}
/* Helper function to recursively
perform DFS from the node */
dfs(node, adj, vis, ans) {
// Mark the node as visited
vis[node] = true;
// Add the node to the result
ans.push(node);
// Traverse all its neighbours
for (const it of adj[node]) {
// If the neighbour is not visited
if (!vis[it]) {
// Perform DFS recursively
this.dfs(it, adj, vis, ans);
}
}
}
/* Function to return a list containing
the DFS traversal of the graph */
dfsOfGraph(V, adj) {
// Visited array
const vis = new Array(V).fill(false);
// Create a list to store DFS
const ans = [];
// Traverse all the nodes
for (let i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Call DFS from that node
this.dfs(i, adj, vis, ans);
}
}
// Return the result
return ans;
}
/* Function to return a list containing
the BFS traversal of the graph */
bfsOfGraph(V, adj) {
// Visited array
const vis = new Array(V).fill(false);
// To store the result
const ans = [];
// Traverse all the nodes
for (let i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Mark the node as visited
vis[i] = true;
// Call BFS from that node
this.bfs(i, adj, vis, ans);
}
}
return ans;
}
}
const main = () => {
const V = 5;
const adj = [
[2, 3, 1],
[0],
[0, 4],
[0],
[2]
];
// Creating instance of Solution class
const sol = new Solution();
// Function call to get the BFS traversal of graph
const bfs = sol.bfsOfGraph(V, adj);
// Function call to get the DFS traversal of graph
const dfs = sol.dfsOfGraph(V, adj);
// Output
console.log("The BFS traversal of the given graph is: ", bfs.join(" "));
console.log("The DFS traversal of the given graph is: ", dfs.join(" "));
}
main();
Complexity Analysis:
Time Complexity: O(V+E) (where E represents the number of edges in the graph)
All the V nodes are traversed during the traversal and all the E edges are processed once taking an overall time complexity of O(V+E).
Space Complexity: O(V)
The BFS traversal uses a queue data structure to process the nodes in a level-order fashion. In the worst case, all the nodes will be present in the queue leading to space requirement of O(V).
Intuition:
The traversal techniques form the basics of any graph problem. One of the two traversal techniques is Depth First Search(DFS). Depth-First Search (DFS) is a traversal technique that explores as far as possible along each branch before backtracking. It uses a stack data structure, either explicitly or implicitly through recursion.
Approach:
- Mark all nodes as unvisited. Create an empty stack or use recursion.
- Push the source node onto the stack (or call the recursive function with the source node). Mark the source node as visited.
- While the stack is not empty:
- Pop the top node from the stack. For each adjacent unvisited node, push the adjacent node onto the stack (or call the recursive function with the adjacent node).
- Mark the adjacent node as visited.
- Repeat the process until all nodes are visited.
Dry Run:
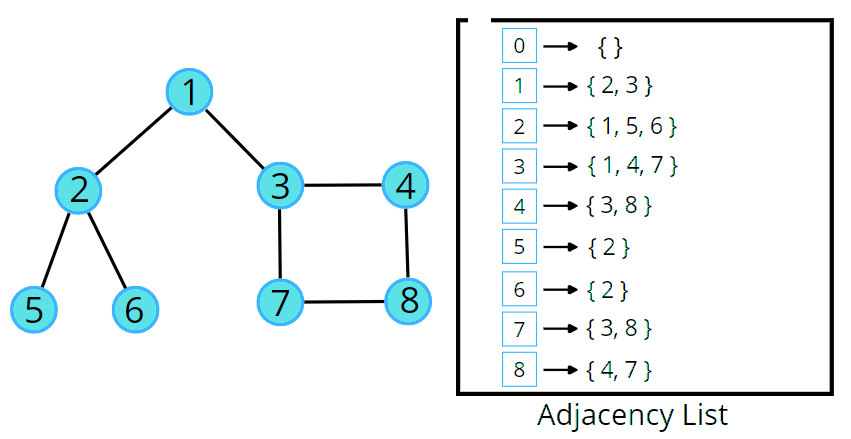
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Helper function to perform BFS
traversal from the node */
void bfs(int node, vector<int> adj[], int vis[],
vector<int> &ans) {
// Queue data structure
queue<int> q;
// Push the starting node
q.push(node);
// Until the queue is empty
while(!q.empty()) {
// Get the node
int node = q.front();
q.pop();
// Add the node to answer
ans.push_back(node);
// Traverse for all its neighbours
for(auto it : adj[node]) {
/* If the neighbour has previously not been
visited, store in Q and mark as visited */
if(!vis[it]) {
vis[it] = 1;
q.push(it);
}
}
}
// Return
return;
}
/* Helper function to recursively
perform DFS from the node */
void dfs(int node, vector<int> adj[], int vis[],
vector<int> &ans) {
// Mark the node as visited
vis[node] = 1;
// Add the node to the result
ans.push_back(node);
// Traverse all its neighbours
for(auto it : adj[node]) {
// If the neighbour is not visited
if(!vis[it]) {
// Perform DFS recursively
dfs(it, adj, vis, ans);
}
}
}
public:
/* Function to return a list containing
the DFS traversal of the graph */
vector<int> dfsOfGraph(int V, vector<int> adj[]) {
// Visited array
int vis[V] = {0};
// Create a list to store DFS
vector<int> ans;
// Traverse all the nodes
for(int i=0; i < V; i++) {
// If the node is unvisited
if(vis[i] == 0) {
// Call DFS from that node
dfs(i, adj, vis, ans);
}
}
// Return the result
return ans;
}
/* Function to return a list containing
the BFS traversal of the graph */
vector<int> bfsOfGraph(int V, vector<int> adj[]) {
// Visited array
int vis[V] = {0};
// To store the result
vector<int> ans;
// Traverse all the nodes
for(int i=0; i < V; i++) {
// If the node is unvisited
if(vis[i] == 0) {
// Mark the node as visited
vis[i] = 1;
// Call BFS from that node
bfs(i, adj, vis, ans);
}
}
return ans;
}
};
int main() {
int V = 5;
vector<int> adj[] = {
{2, 3, 1},
{0},
{0, 4},
{0},
{2}
};
// Creating instance of Solution class
Solution sol;
// Function call to get the BFS traversal of graph
vector<int> bfs = sol.bfsOfGraph(V, adj);
// Function call to get the BFS traversal of graph
vector<int> dfs = sol.dfsOfGraph(V, adj);
// Output
cout << "The BFS traversal of the given graph is: ";
for(int i=0; i < bfs.size(); i++) {
cout << bfs[i] << " ";
}
cout << "\nThe DFS traversal of the given graph is: ";
for(int i=0; i < dfs.size(); i++) {
cout << dfs[i] << " ";
}
return 0;
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
import java.util.*;
class Solution {
/* Helper function to perform BFS
traversal from the node */
private void bfs(int node, List<Integer>[] adj, boolean[] vis,
List<Integer> ans) {
// Queue data structure
Queue<Integer> q = new LinkedList<>();
// Push the starting node
q.add(node);
// Until the queue is empty
while (!q.isEmpty()) {
// Get the node
int current = q.poll();
// Add the node to answer
ans.add(current);
// Traverse for all its neighbours
for (int it : adj[current]) {
/* If the neighbour has previously not been
visited, store in Q and mark as visited */
if (!vis[it]) {
vis[it] = true;
q.add(it);
}
}
}
}
/* Helper function to recursively
perform DFS from the node */
private void dfs(int node, List<Integer>[] adj, boolean[] vis,
List<Integer> ans) {
// Mark the node as visited
vis[node] = true;
// Add the node to the result
ans.add(node);
// Traverse all its neighbours
for (int it : adj[node]) {
// If the neighbour is not visited
if (!vis[it]) {
// Perform DFS recursively
dfs(it, adj, vis, ans);
}
}
}
/* Function to return a list containing
the DFS traversal of the graph */
public List<Integer> dfsOfGraph(int V, List<Integer>[] adj) {
// Visited array
boolean[] vis = new boolean[V];
// Create a list to store DFS
List<Integer> ans = new ArrayList<>();
// Traverse all the nodes
for (int i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Call DFS from that node
dfs(i, adj, vis, ans);
}
}
// Return the result
return ans;
}
/* Function to return a list containing
the BFS traversal of the graph */
public List<Integer> bfsOfGraph(int V, List<Integer>[] adj) {
// Visited array
boolean[] vis = new boolean[V];
// To store the result
List<Integer> ans = new ArrayList<>();
// Traverse all the nodes
for (int i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Mark the node as visited
vis[i] = true;
// Call BFS from that node
bfs(i, adj, vis, ans);
}
}
return ans;
}
public static void main(String[] args) {
int V = 5;
List<Integer>[] adj = new List[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
adj[0].addAll(Arrays.asList(2, 3, 1));
adj[1].add(0);
adj[2].addAll(Arrays.asList(0, 4));
adj[3].add(0);
adj[4].add(2);
// Creating instance of Solution class
Solution sol = new Solution();
// Function call to get the BFS traversal of graph
List<Integer> bfs = sol.bfsOfGraph(V, adj);
// Function call to get the DFS traversal of graph
List<Integer> dfs = sol.dfsOfGraph(V, adj);
// Output
System.out.println("The BFS traversal of the given graph is: " + bfs);
System.out.println("The DFS traversal of the given graph is: " + dfs);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109
from collections import deque
class Solution:
# Helper function to perform BFS
# traversal from the node
def bfs(self, node, adj, vis, ans):
# Queue data structure
q = deque()
# Push the starting node
q.append(node)
# Until the queue is empty
while q:
# Get the node
node = q.popleft()
# Add the node to answer
ans.append(node)
# Traverse for all its neighbours
for it in adj[node]:
# If the neighbour has previously not been
# visited, store in Q and mark as visited
if not vis[it]:
vis[it] = 1
q.append(it)
# Helper function to recursively
# perform DFS from the node
def dfs(self, node, adj, vis, ans):
# Mark the node as visited
vis[node] = 1
# Add the node to the result
ans.append(node)
# Traverse all its neighbours
for it in adj[node]:
# If the neighbour is not visited
if not vis[it]:
# Perform DFS recursively
self.dfs(it, adj, vis, ans)
# Function to return a list containing
# the DFS traversal of the graph
def dfsOfGraph(self, V, adj):
# Visited array
vis = [0] * V
# Create a list to store DFS
ans = []
# Traverse all the nodes
for i in range(V):
# If the node is unvisited
if vis[i] == 0:
# Call DFS from that node
self.dfs(i, adj, vis, ans)
# Return the result
return ans
# Function to return a list containing
# the BFS traversal of the graph
def bfsOfGraph(self, V, adj):
# Visited array
vis = [0] * V
# To store the result
ans = []
# Traverse all the nodes
for i in range(V):
# If the node is unvisited
if vis[i] == 0:
# Mark the node as visited
vis[i] = 1
# Call BFS from that node
self.bfs(i, adj, vis, ans)
return ans
if __name__ == "__main__":
V = 5
adj = [
[2, 3, 1],
[0],
[0, 4],
[0],
[2]
]
# Creating instance of Solution class
sol = Solution()
# Function call to get the BFS traversal of graph
bfs = sol.bfsOfGraph(V, adj)
# Function call to get the DFS traversal of graph
dfs = sol.dfsOfGraph(V, adj)
# Output
print("The BFS traversal of the given graph is: ", bfs)
print("The DFS traversal of the given graph is: ", dfs)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123
class Solution {
/* Helper function to perform BFS
traversal from the node */
bfs(node, adj, vis, ans) {
// Queue data structure
const q = [];
// Push the starting node
q.push(node);
// Until the queue is empty
while (q.length > 0) {
// Get the node
const current = q.shift();
// Add the node to answer
ans.push(current);
// Traverse for all its neighbours
for (const it of adj[current]) {
/* If the neighbour has previously not been
visited, store in Q and mark as visited */
if (!vis[it]) {
vis[it] = true;
q.push(it);
}
}
}
}
/* Helper function to recursively
perform DFS from the node */
dfs(node, adj, vis, ans) {
// Mark the node as visited
vis[node] = true;
// Add the node to the result
ans.push(node);
// Traverse all its neighbours
for (const it of adj[node]) {
// If the neighbour is not visited
if (!vis[it]) {
// Perform DFS recursively
this.dfs(it, adj, vis, ans);
}
}
}
/* Function to return a list containing
the DFS traversal of the graph */
dfsOfGraph(V, adj) {
// Visited array
const vis = new Array(V).fill(false);
// Create a list to store DFS
const ans = [];
// Traverse all the nodes
for (let i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Call DFS from that node
this.dfs(i, adj, vis, ans);
}
}
// Return the result
return ans;
}
/* Function to return a list containing
the BFS traversal of the graph */
bfsOfGraph(V, adj) {
// Visited array
const vis = new Array(V).fill(false);
// To store the result
const ans = [];
// Traverse all the nodes
for (let i = 0; i < V; i++) {
// If the node is unvisited
if (!vis[i]) {
// Mark the node as visited
vis[i] = true;
// Call BFS from that node
this.bfs(i, adj, vis, ans);
}
}
return ans;
}
}
const main = () => {
const V = 5;
const adj = [
[2, 3, 1],
[0],
[0, 4],
[0],
[2]
];
// Creating instance of Solution class
const sol = new Solution();
// Function call to get the BFS traversal of graph
const bfs = sol.bfsOfGraph(V, adj);
// Function call to get the DFS traversal of graph
const dfs = sol.dfsOfGraph(V, adj);
// Output
console.log("The BFS traversal of the given graph is: ", bfs.join(" "));
console.log("The DFS traversal of the given graph is: ", dfs.join(" "));
}
main();
Complexity Analysis:
Time Complexity: O(V+E) (where E represents the number of edges in the graph)
All the V nodes are traversed during the traversal and all the E edges are processed once taking an overall time complexity of O(V+E).
Space Complexity: O(V)
The DFS traversal uses a stack data structure or recursive stack space to process the nodes in a depth-first fashion. In the worst case, all the nodes will be present in the stack leading to space requirement of O(V).
Frequently Occurring Doubts
Q: Why does DFS use a stack while BFS uses a queue?
A: DFS explores deep first, requiring backtracking, so recursion or an explicit stack is used. BFS explores all neighbors before moving deeper, requiring a queue (FIFO order).
Q: What happens if the graph contains cycles?
A: DFS may revisit nodes without a visited array`, leading to infinite recursion. BFS correctly handles cycles by ensuring each node is processed only once.
Interview Followup Questions
Q: How would you modify DFS/BFS to find the shortest path in an unweighted graph?
A: Use BFS, as it guarantees the shortest path in O(V + E). Track parent nodes to reconstruct the path.
Q: How would you modify DFS to detect cycles in the graph?
A: Maintain a recursion stack (visited[i] == True while in recursion) to detect back edges.
Notes
Code
✅ Testcase
Input: {'V': '5', 'edges': '[[0, 2], [0, 3], [0, 1], [2, 4]]'}
Expected:
0 2 4 3 1
0 2 3 1 4
0 2 4 3 1
0 2 3 1 4
Actual: -
Time: -
sec
Status: Waiting
Input: {'V': '4', 'edges': '[[0, 1], [0, 3], [1, 2]]'}
Expected:
0 1 2 3
0 1 3 2
0 1 2 3
0 1 3 2
Actual: -
Time: -
sec
Status: Waiting
Input: {'V': '3', 'edges': '[[0,1],[0,2]]'}
Expected:
0 1 2
0 1 2
0 1 2
0 1 2
Actual: -
Time: -
sec
Status: Waiting
Facts
- • Fun Fact: The techniques of Depth First Search (DFS) and Breadth First Search (BFS) that this problem explores are widely used in real-world routing algorithms, like Google Maps
- • They need to traverse through a huge graph of roads and intersections (vertices) and find the shortest or fastest path
- • Moreover, DFS is also used in web-crawlers of search engines like Google to visit and index new webpages, wherein the link structure of the websites is treated as a graph