Insert a given node in BST
Binary Search Trees
Medium
Medium
- The problem underlying this concept is extensively used in the development of databases
- When adding new records, most databases use binary search trees (specifically, B-trees or B+ trees), or variants of them, to maintain sorted data and ensure fast search, insert, and delete operations
- This way, when you look up a piece of information in a large database, the engine will use binary search trees to quickly locate the data you need
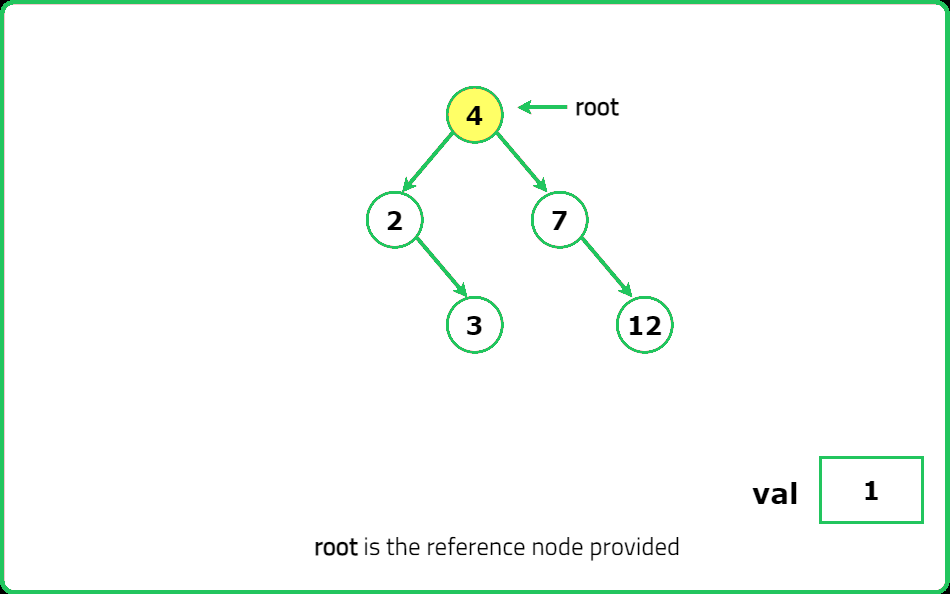
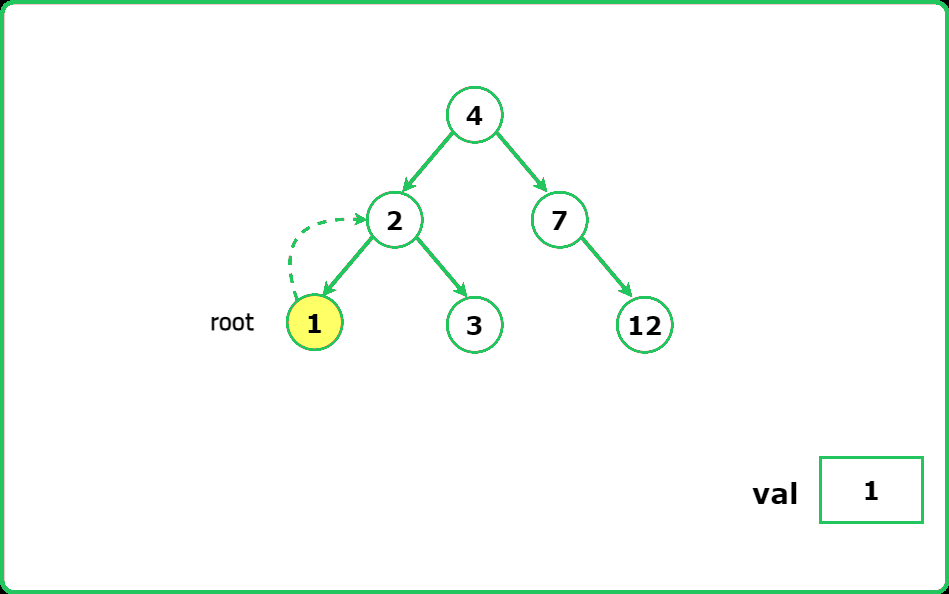
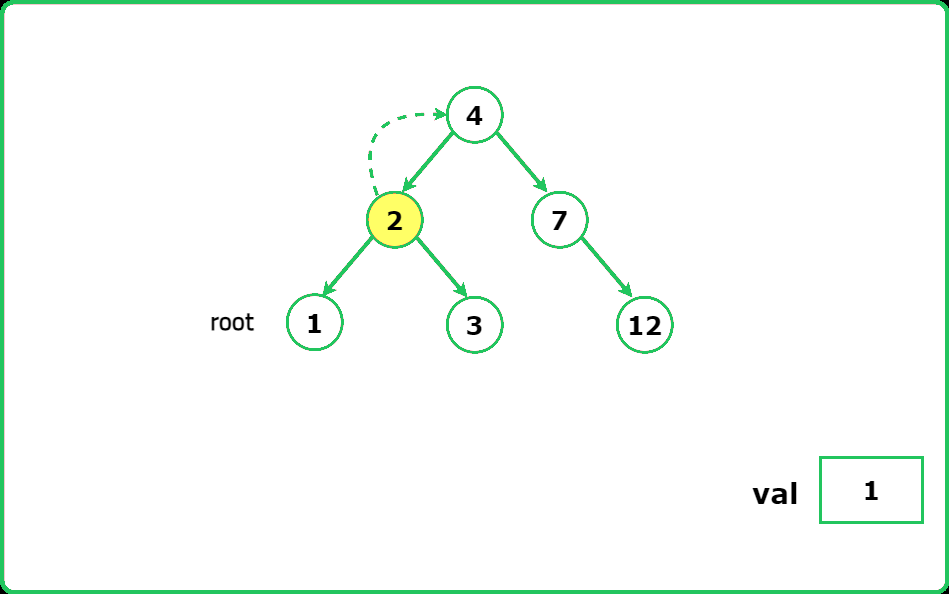
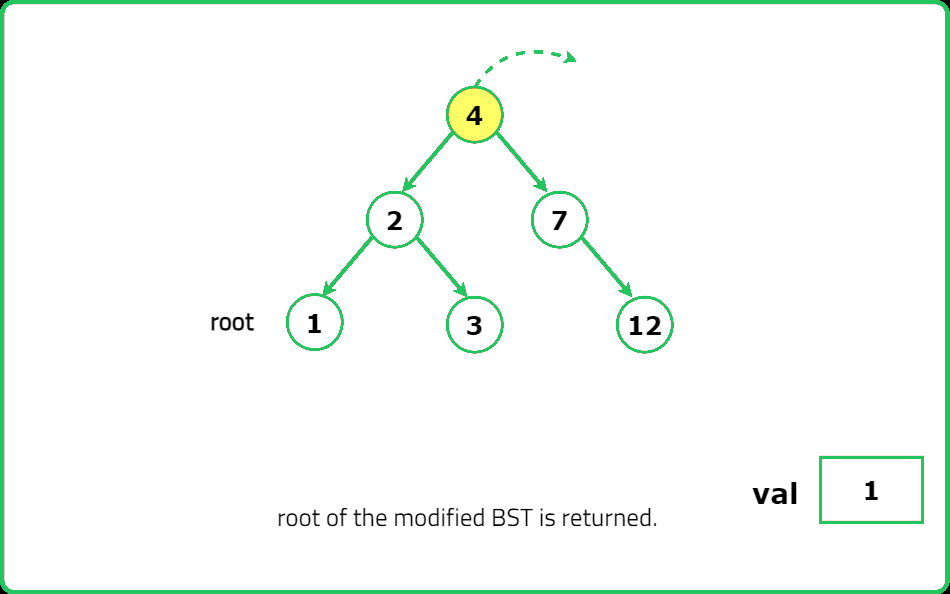
Given the root node of a binary search tree (BST) and a value val to insert into the tree. Return the root node of the BST after the insertion.
It is guaranteed that the new value does not exist in the original BST. Note that the compiler output shows true if the node is added correctly, else false.
Examples:
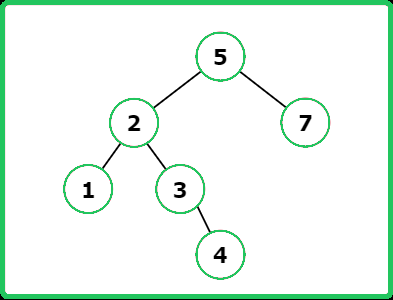
Input : root = [4, 2, 7, 1, 3] , val = 5
Output : [4, 2, 7, 1, 3, 5]
Explanation : Below is image where the node 5 is inserted
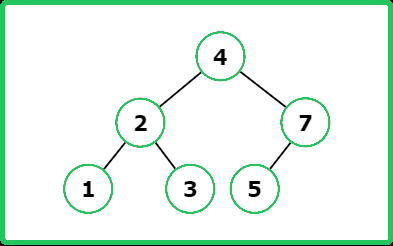
There is another way to insert the given val as shown below.
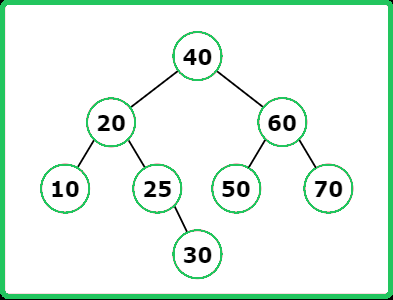
Input : root = [40, 20, 60, 10, 30, 50, 70] , val = 25
Output : [40, 20, 60, 10, 25, 50, 70, null, null, null, 30]
Explanation : Below is image where the node 25 is inserted
Input : root = [4, 2, 7, 1, null, 6] , val = 3
Constraints
- 1 <= Number of nodes <= 104
- -108 <= Node.val <= 108
- All values in tree are unique.
- -108 <= val <= 108
- It is guaranteed that the val does not exists in original BST.
Hints
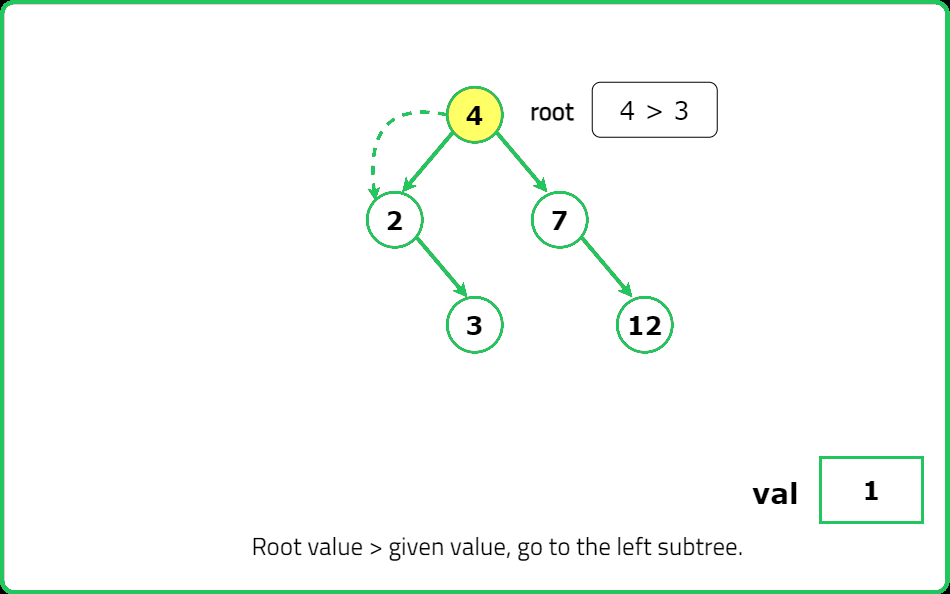
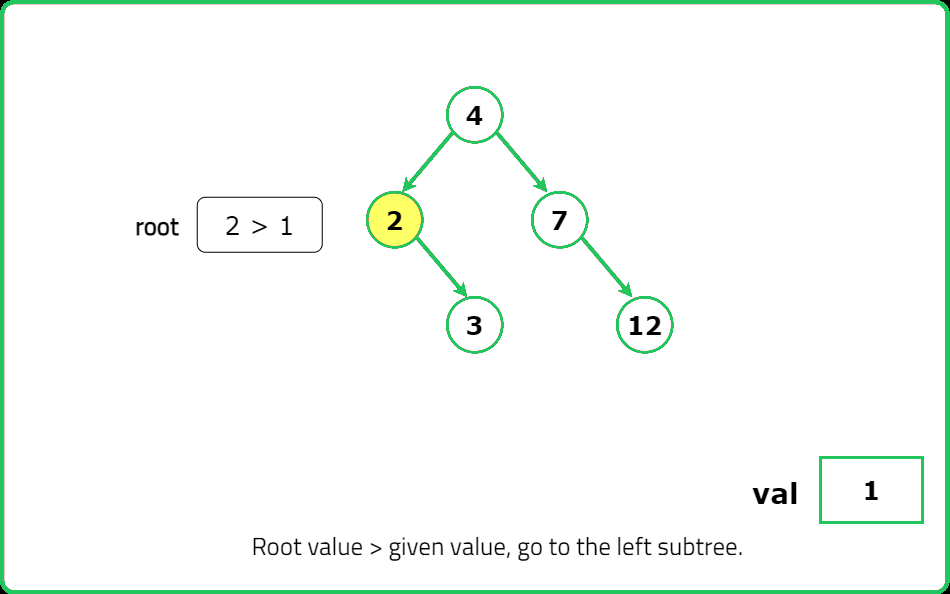
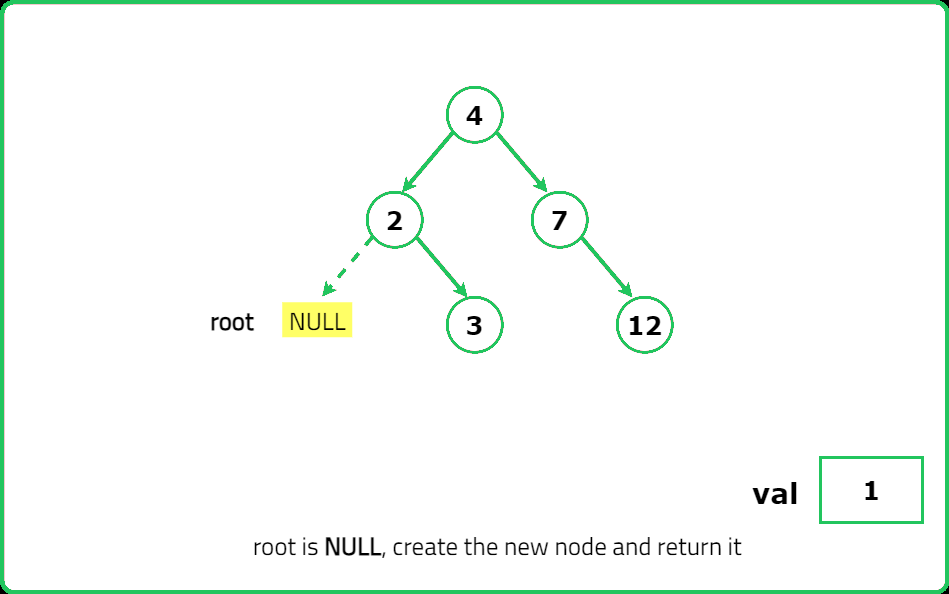
- If root == null, create a new node with val and return it. If val < root.val, insert val into the left subtree (root.left). If val > root.val, insert val into the right subtree (root.right). Return the root node after insertion.
- Start from the root and traverse the tree. If val < current.val, move left. If val > current.val, move right. When an empty spot (null) is found, create a new node and attach it. Return the original root.
Company Tags
Bain & Company
Philips Healthcare
Zomato
Zynga
eBay
Square
Epic Games
Siemens Healthineers
JPMorgan Chase
Rakuten
Freshworks
Rockstar Games
Shopify
Pinterest
Bloomberg
Texas Instruments
Broadcom
PwC
Cerner
HCL Technologies
Electronic Arts
Dropbox
Uber
Optum
Johnson & Johnson
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe