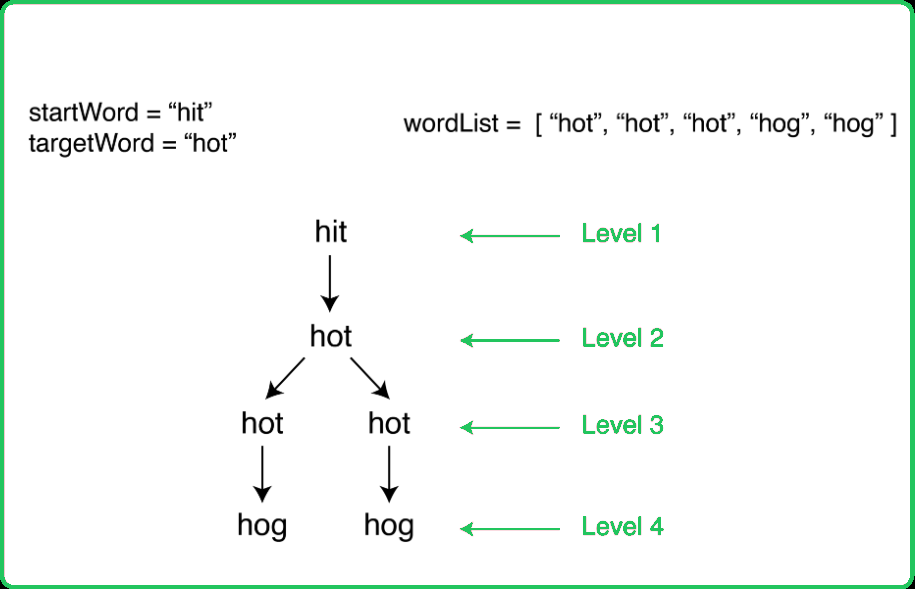
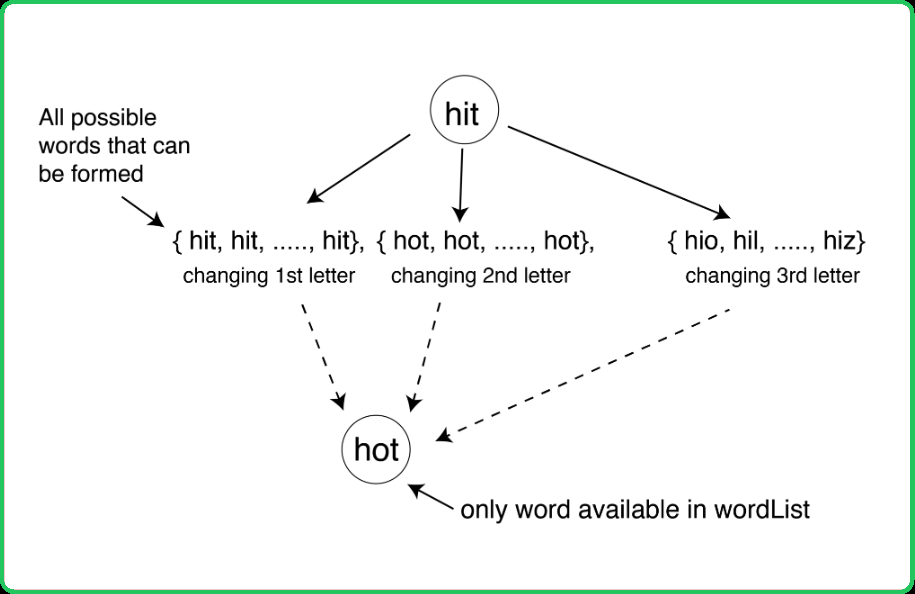
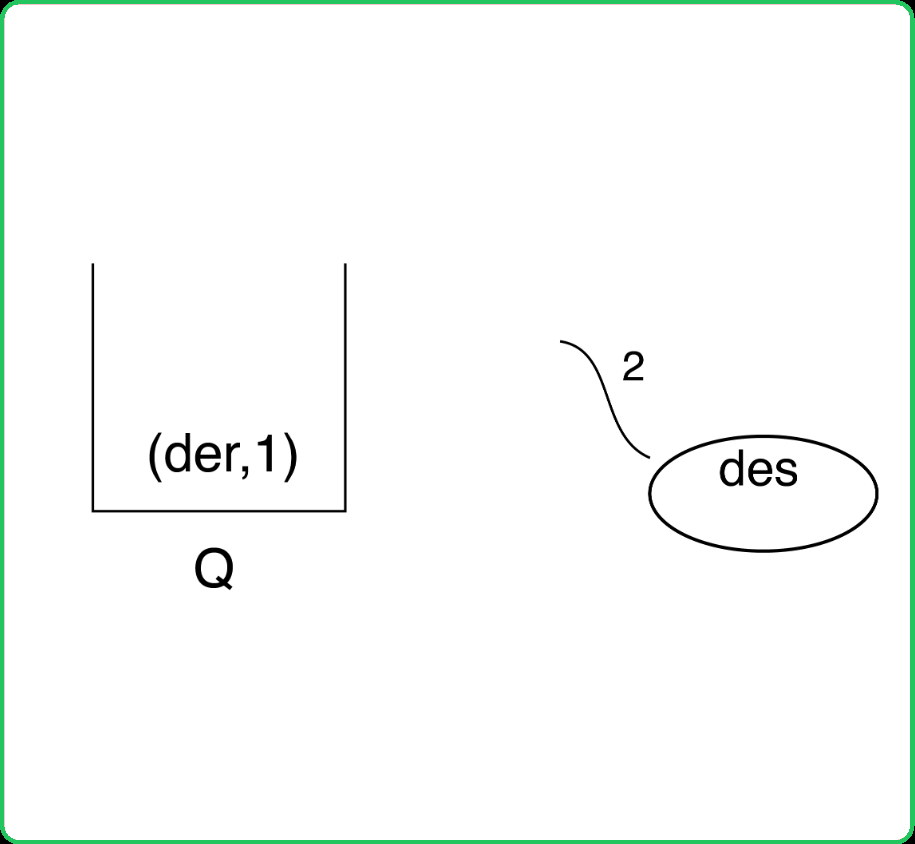
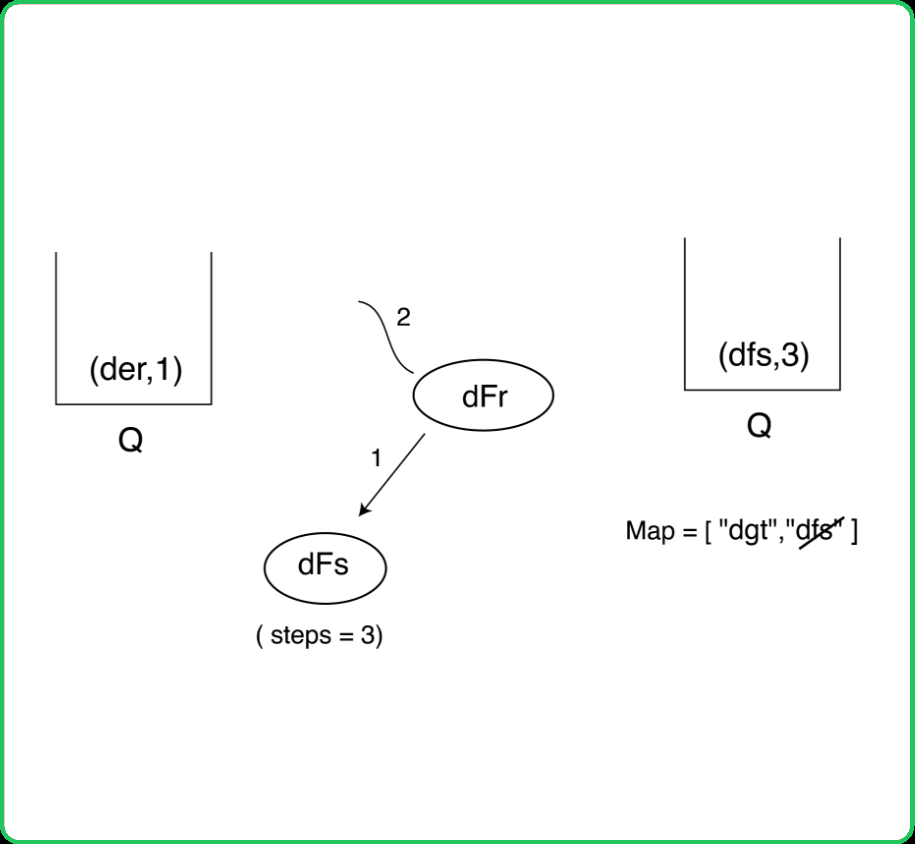
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to determine number of steps
to reach from start ward to target word */
int wordLadderLength(string startWord,
string targetWord,
vector<string> &wordList) {
/* Queue data structure to store pair:
{"word", steps to reach "word"} */
queue<pair<string, int>> q;
// Add the starting word to queue
q.push({startWord, 1});
// Add all the words to a hashset
unordered_set<string> st(wordList.begin(),
wordList.end() );
/* Erase the starting word
from set (if it exists) */
st.erase(startWord);
// Until the queue is empty
while (!q.empty()){
// Get the word from queue
string word = q.front().first;
// Get the steps from queue
int steps = q.front().second;
q.pop();
// Return steps if target word is acheived
if (word == targetWord)
return steps;
// Iterate on every character
for (int i=0; i < word.size(); i++) {
// Store the original letter
char original = word[i];
/* Replacing current character with
letters from 'a' to 'z' to match
any possible word from set */
for (char ch = 'a'; ch <= 'z'; ch++) {
word[i] = ch;
// Check if it exists in the set
if (st.find(word) != st.end()) {
// Erase the word from set
st.erase(word);
// Add the transition to the queue
q.push({word, steps + 1});
}
}
// Update the original letter back
word[i] = original;
}
}
/* If no transformation sequence
is found, return 0 */
return 0;
}
};
int main() {
string startWord = "der", targetWord = "dfs";
vector<string> wordList =
{"des","der","dfr","dgt","dfs"};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to determine number of
steps to reach from start ward to target word */
int ans =
sol.wordLadderLength(startWord, targetWord, wordList);
// Output
cout << "Word ladder length is: " << ans;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105
import java.util.*;
class Solution {
/* Function to determine number of steps
to reach from start ward to target word */
public int wordLadderLength(String startWord,
String targetWord,
List<String> wordList) {
/* Queue data structure to store pair:
{"word", steps to reach "word"} */
Queue<Pair> q = new LinkedList<>();
// Add the starting word to queue
q.add(new Pair(startWord, 1));
// Add all the words to a hashset
Set<String> st = new HashSet<>(wordList);
/* Erase the starting word
from set (if it exists) */
st.remove(startWord);
// Until the queue is empty
while (!q.isEmpty()){
// Get the word from queue
String word = q.peek().word;
// Get the steps from queue
int steps = q.peek().steps;
q.poll();
// Return steps if target word is achieved
if (word.equals(targetWord))
return steps;
// Iterate on every character
for (int i = 0; i < word.length(); i++) {
// Store the original letter
char original = word.charAt(i);
/* Replacing current character with
letters from 'a' to 'z' to match
any possible word from set */
for (char ch = 'a'; ch <= 'z'; ch++) {
char[] wordArray = word.toCharArray();
wordArray[i] = ch;
String newWord = new String(wordArray);
// Check if it exists in the set
if (st.contains(newWord)) {
// Erase the word from set
st.remove(newWord);
// Add the transition to the queue
q.add(new Pair(newWord, steps + 1));
}
}
// Update the original letter back
word = word.substring(0, i) + original +
word.substring(i + 1);
}
}
/* If no transformation sequence
is found, return 0 */
return 0;
}
// Custom Pair class
static class Pair {
String word;
int steps;
Pair(String word, int steps) {
this.word = word;
this.steps = steps;
}
}
public static void main(String[] args) {
String startWord = "der", targetWord = "dfs";
List<String> wordList =
Arrays.asList("des", "der", "dfr", "dgt", "dfs");
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to determine number of
steps to reach from start ward to target word */
int ans =
sol.wordLadderLength(startWord, targetWord, wordList);
// Output
System.out.println("Word ladder length is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
from collections import deque
class Solution:
# Function to determine number of steps
# to reach from start ward to target word
def wordLadderLength(self, startWord,
targetWord, wordList):
# Queue data structure to store pair:
# {"word", steps to reach "word"}
q = deque([(startWord, 1)])
# Add all the words to a hashset
st = set(wordList)
# Erase the starting word
# from set (if it exists)
st.discard(startWord)
# Until the queue is empty
while q:
# Get the word from queue
word, steps = q.popleft()
# Return steps if target word is achieved
if word == targetWord:
return steps
# Iterate on every character
for i in range(len(word)):
# Store the original letter
original = word[i]
# Replacing current character with
# letters from 'a' to 'z' to match
# any possible word from set
for ch in range(ord('a'), ord('z') + 1):
word = word[:i] + chr(ch) + word[i+1:]
# Check if it exists in the set
if word in st:
# Erase the word from set
st.remove(word)
# Add the transition to the queue
q.append((word, steps + 1))
# Update the original letter back
word = word[:i] + original + word[i+1:]
# If no transformation sequence
# is found, return 0
return 0
if __name__ == "__main__":
startWord = "der"
targetWord = "dfs"
wordList = ["des", "der", "dfr", "dgt", "dfs"]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to determine number of
# steps to reach from start ward to target word
ans = sol.wordLadderLength(startWord, targetWord, wordList)
# Output
print("Word ladder length is:", ans)
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879
class Solution {
/* Function to determine number of steps
to reach from start ward to target word */
wordLadderLength(startWord, targetWord, wordList) {
/* Queue data structure to store pair:
{"word", steps to reach "word"} */
let q = [{ word: startWord, steps: 1 }];
// Add all the words to a hashset
let st = new Set(wordList);
/* Erase the starting word
from set (if it exists) */
st.delete(startWord);
// Until the queue is empty
while (q.length > 0) {
// Get the word from queue
let { word, steps } = q.shift();
// Return steps if target word is achieved
if (word === targetWord)
return steps;
// Iterate on every character
for (let i = 0; i < word.length; i++) {
// Store the original letter
let original = word[i];
/* Replacing current character with
letters from 'a' to 'z' to match
any possible word from set */
for (let ch = 97; ch <= 122; ch++) {
word = word.substring(0, i) +
String.fromCharCode(ch) +
word.substring(i + 1);
// Check if it exists in the set
if (st.has(word)) {
// Erase the word from set
st.delete(word);
// Add the transition to the queue
q.push({ word, steps: steps+1 });
}
}
// Update the original letter back
word = word.substring(0, i) +
original +
word.substring(i + 1);
}
}
/* If no transformation sequence
is found, return 0 */
return 0;
}
}
const startWord = "der", targetWord = "dfs";
const wordList = ["des","der","dfr","dgt","dfs"];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to determine number of
steps to reach from start ward to target word */
const ans =
sol.wordLadderLength(startWord, targetWord, wordList);
// Output
console.log("Word ladder length is:", ans);