Best time to buy and sell stock IV

Upon observation, we find that every day, there will be two choices, either to do nothing and move to the next day or to buy/sell (based on the last transaction and the number of transactions left) and find out the profit. Therefore we need to generate all the choices in order to compare the profit. As all possible choices needs to be generated, we will use recursion.

This question is quite similar to the question discussed in Buy and Sell Stock III. There at most two transactions were allowed, whereas in this problem we can do at most 'K' transactions. Therefore, we will modify that approach according to our needs in this section.

Steps to form the recursive solution:

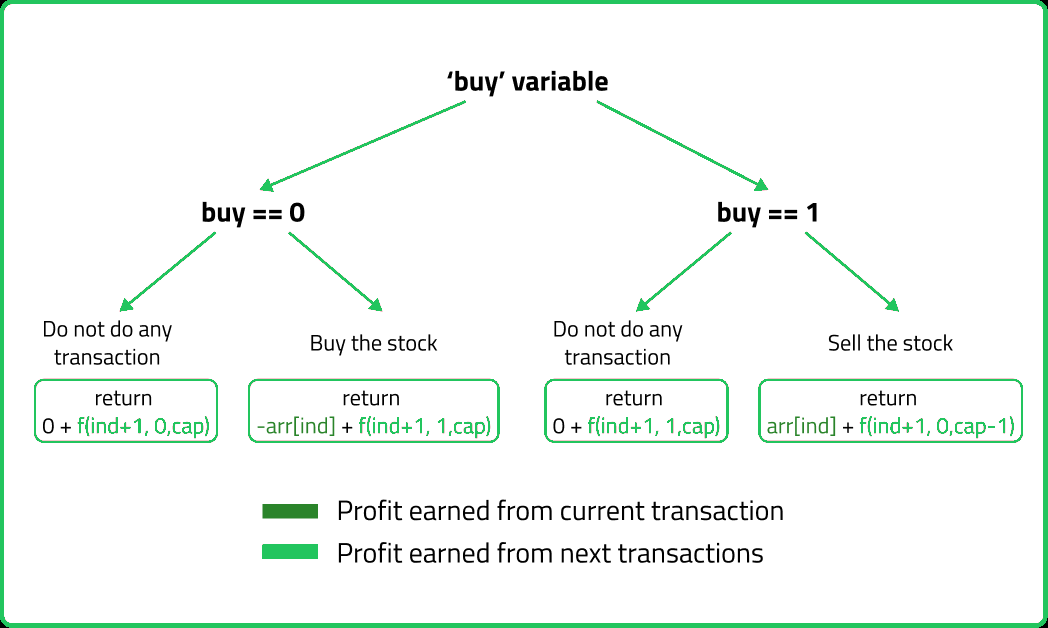
Express the problem in terms of indexes: We need to think in the terms of the number of days, therefore one variable will be the array index( say ind). Next, we need to consider the condition that a stock can't be bought again, that is we need to first sell a stock, and then we can buy that again. Therefore a second variable ‘buy’ is needed, which tells, on a particular day whether we can buy or sell the stock. Next, there is a limit on the number of transactions that can be made. Here the initial cap is 'k'. So in order to keep track of this constraint, one more variable will be needed (say 'cap').

f(ind, buy, cap) will give the maximum profit that can be generated from day 'ind' to day (n-1), where 'buy' tells that whether we need to buy or sell the stock at day 'ind' and 'cap' tells the number of transactions left.

Try out all possible choices at a given index: Every day, there will be two choices, either to buy/sell the stock(based on the buy variable’s value) or to do nothing and move on to the next day. As we need to generate all the choices, use the pick/non-pick technique to the same.

Case 1: When buy == 0, the stock can be bought. If we can buy the stock on a particular day, there will be two options:

Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1, 0, cap). As we have not bought the stock, the ‘buy’ variable value will still remain 0, indicating that stock can be bought on next day. And the ‘cap’ variable will remain the same as if no transaction took place.

Option 2: The other option is to buy the stock on the current day. In this case, the net profit earned from the current transaction will be -Arr[i]. As we are buying the stock, we are giving money out of our pocket, therefore the profit we earn is negative. To calculate the maximum profit starting from the next day, recursively call f(ind+1,1, cap). As the stock has been bought, the ‘buy’ variable value will change to 1, indicating that we can’t buy and only sell the stock the next day. As we have only bought the stock and not sold it the transaction remains incomplete and the ‘cap’ variable value remains unchanged.

Case 2: When buy == 1, we can sell the stock. If we can sell the stock on a particular day, we will have two options:

Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1,1, cap). As we have not bought the stock, the ‘buy’ variable value will still remain at 1, indicating that we can’t buy and only sell the stock the next day. And the ‘cap’ variable will remain the same as if no transaction took place.

Option 2: The other option is to sell the stock on the current day. In this case, the net profit earned from the current transaction will be +Arr[i]. As we are selling the stock, we are putting the money into our pocket, therefore the profit we earn is positive. To calculate the maximum profit starting from the next day, we will recursively call f(ind+1,0,cap-1). As we have sold the stock, the ‘buy’ variable value will change to 0, indicating that we can buy the stock the next day. As we have sold the earlier bought stock, we make one complete transaction, therefore now we update the ‘cap’ variable’s value to cap-1.

Note: Buying and selling a stock together counts as one complete transaction.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, buy, cap){
    //Base case
    if(buy == 0){
        op1 = 0 + f(ind + 1, 0, cap)
        op2 = -arr[ind] + f(ind + 1, 1, cap)
    }
    if(buy == 1){
        op1 = 0 + f(ind + 1, 1, cap)
        op2 = arr[ind] + f(ind + 1, 0, cap-1)
    }
           
}

Take the maximum of all choices: As we are looking to maximize the profit earned, return the maximum value in both cases.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, buy, cap){
    //Base case
    if(buy == 0){
        op1 = 0 + f(ind + 1, 0, cap)
        op2 = -arr[ind] + f(ind + 1, 1, cap)
    }
    if(buy == 1){
        op1 = 0 + f(ind + 1, 1, cap)
        op2 = arr[ind] + f(ind + 1, 0, cap-1)
    }
    return max(op1, op2)    
}

Base cases: There be will two base cases, when ind==n, it means we have finished trading on all days, and no more profit can be made, therefore simply return 0. Second base case is when cap==0, it means that we cannot make any more transactions. Therefore return 0.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    //Function to find the maximum profit earned using recursion
    int func(int ind, int buy, int cap, int n, vector<int> &arr) {
        // Base case 
        if (ind == n || cap == 0) {
            return 0;
        }

        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = max(0 + func(ind + 1, 0, cap, n, arr), (-1)*arr[ind] + func(ind + 1, 1, cap, n, arr));
        }
        
        //We can sell the stock
        if (buy == 1) { 
            profit = max(0 + func(ind + 1, 1, cap, n, arr), arr[ind] + func(ind + 1, 0, cap-1, n, arr));
        }

        // Return the calculated profit
        return profit;
    }
public:
    //Function to calculate the maximum profit earned 
    int stockBuySell(vector<int> &arr, int n, int k) {
        if (n == 0) 
            return 0;

        int ans = func(0, 0, k, n, arr);
        
        //Return the maximum profit
        return ans;
    }
};
int main() {
    int n = 8;
    vector<int> arr = {3, 3, 5, 0, 0, 3, 1, 4};
    int k = 3;
    
    //Create an instance of Solution class
    Solution sol;

    // Call the stockBuySell function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(arr, n, k);

    return 0;
}
import java.util.*;

class Solution {
    // Function to find the maximum profit earned using recursion
    private int func(int ind, int buy, int cap, int n, int[] arr) {
        // Base case 
        if (ind == n || cap == 0) {
            return 0;
        }

        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = Math.max(0 + func(ind + 1, 0, cap, n, arr), (-1)*arr[ind] + func(ind + 1, 1, cap, n, arr));
        }
        
        // We can sell the stock
        if (buy == 1) { 
            profit = Math.max(0 + func(ind + 1, 1, cap, n, arr), arr[ind] + func(ind + 1, 0, cap-1, n, arr));
        }

        // Return the calculated profit
        return profit;
    }

    // Function to calculate the maximum profit earned 
    public int stockBuySell(int[]arr, int n, int k) {
        if (n == 0) 
            return 0;

        int ans = func(0, 0, k, n, arr);
        
        // Return the maximum profit
        return ans;
    }

    public static void main(String[] args) {
        int n = 8;
        int[] arr = {3, 3, 5, 0, 0, 3, 1, 4};
        int k = 3;
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the stockBuySell function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(arr, n, k));
    }
}
class Solution:
    # Function to find the maximum profit earned using recursion
    def func(self, ind, buy, cap, n, arr):
        # Base case 
        if(ind == n or cap == 0):
            return 0

        profit = 0
        
        # We can buy the stock
        if buy == 0:
            profit = max(0 + self.func(ind + 1, 0, cap, n, arr), (-1)*arr[ind] + self.func(ind + 1, 1, cap, n, arr))
        
        # We can sell the stock
        if buy == 1:
            profit = max(0 + self.func(ind + 1, 1, cap, n, arr), arr[ind] + self.func(ind + 1, 0, cap-1, n, arr))

        # Return the calculated profit
        return profit

    # Function to calculate the maximum profit earned 
    def stockBuySell(self, arr, n, k):
        if n == 0:
            return 0

        ans = self.func(0, 0, k, n, arr)
        
        # Return the maximum profit
        return ans

if __name__ == "__main__":
    n = 8
    arr = [3, 3, 5, 0, 0, 3, 1, 4]
    k = 3
    
    # Create an instance of Solution class
    sol = Solution()

    # Call the stockBuySell function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(arr, n, k))
class Solution {
    // Function to find the maximum profit earned using recursion
    func(ind, buy, cap, n, arr) {
        // Base case 
        if (ind === n || cap === 0) {
            return 0;
        }

        let profit = 0;
        
        // We can buy the stock
        if (buy === 0) { 
            profit = Math.max(0 + this.func(ind + 1, 0, cap, n, arr), (-1)*arr[ind] + this.func(ind + 1, 1, cap, n, arr));
        }
        
        // We can sell the stock
        if (buy === 1) { 
            profit = Math.max(0 + this.func(ind + 1, 1, cap, n, arr), arr[ind] + this.func(ind + 1, 0, cap-1, n, arr));
        }

        // Return the calculated profit
        return profit;
    }

    // Function to calculate the maximum profit earned 
    stockBuySell(arr, n, k) {
        if (n === 0) 
            return 0;

        let ans = this.func(0, 0, k, n, arr);
        
        // Return the maximum profit
        return ans;
    }
}

function main() {
    const n = 8;
    const arr = [3, 3, 5, 0, 0, 3, 1, 4];
    const k = 3;
    
    // Create an instance of Solution class
    const sol = new Solution();

    // Call the stockBuySell function and print the result
    console.log("The maximum profit that can be generated is", sol.stockBuySell(arr, n, k));
}

main();

Time Complexity: O(2^(N)), where N is the number of row. As, for each index, ther are two possible options.

Space Complexity:O(N), at maximum the depth of the recursive stack can go upto N.

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

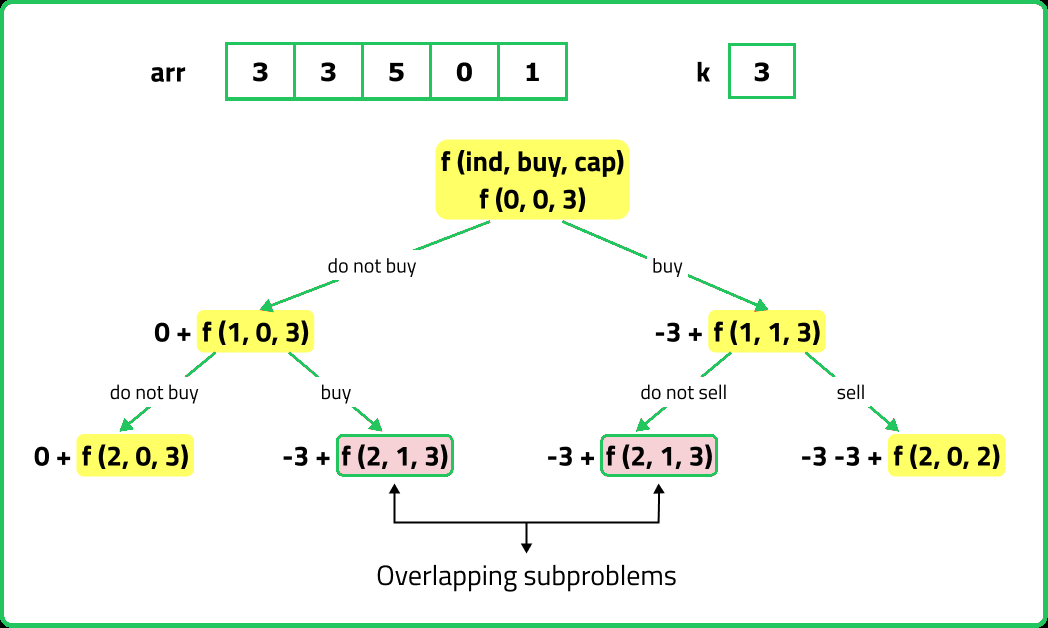
In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][2][k+1]: As there are three changing parameters in the recursive solution, 'ind', 'buy' and 'cap'. The maximum value 'ind' can attain is (n), where n is the size of array, for 'buy' only two values possible 0, 1 and lastly 'cap' can take k+1 values 0 to k as transaction limit is given as 'k' in this problem.

The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    //Function to find the maximum profit earned using memoization
    int func(int ind, int buy, int cap, int n, vector<int> &arr, vector<vector<vector<int>>>& dp) {
        // Base case 
        if (ind == n || cap == 0) {
            return 0;
        }
        /* If the result for this state has 
        already been calculated, return it*/
        if (dp[ind][buy][cap] != -1) {
            return dp[ind][buy][cap];
        }
        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = max(0 + func(ind + 1, 0, cap, n, arr, dp), (-1)*arr[ind] + func(ind + 1, 1, cap, n, arr, dp));
        }
        
        //We can sell the stock
        if (buy == 1) { 
            profit = max(0 + func(ind + 1, 1, cap, n, arr, dp), arr[ind] + func(ind + 1, 0, cap-1, n, arr, dp));
        }

        /* Store the value in dp array and
        return the calculated profit */
        return dp[ind][buy][cap] = profit;
    }
public:
    //Function to calculate the maximum profit earned 
    int stockBuySell(vector<int> &arr, int n, int k) {
        if (n == 0) 
            return 0;
            
        // Initialize a DP table to memoize results
        vector<vector<vector<int>>> dp(n, vector<vector<int>>(2, vector<int>(k+1, -1)));

        int ans = func(0, 0, k, n, arr, dp);
        
        //Return the maximum profit
        return ans;
    }
};
int main() {
    int n = 8;
    vector<int> arr = {3, 3, 5, 0, 0, 3, 1, 4};
    int k = 3;
    
    //Create an instance of Solution class
    Solution sol;

    // Call the stockBuySell function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(arr, n, k);

    return 0;
}


import java.util.*;

class Solution {
    // Function to find the maximum profit earned using memoization
    private int func(int ind, int buy, int cap, int n, int[] arr, int[][][] dp) {
        // Base case 
        if (ind == n || cap == 0) {
            return 0;
        }
        /* If the result for this state has 
        already been calculated, return it*/
        if (dp[ind][buy][cap] != -1) {
            return dp[ind][buy][cap];
        }
        int profit = 0;
        
        // We can buy the stock
        if (buy == 0) { 
            profit = Math.max(0 + func(ind + 1, 0, cap, n, arr, dp), (-1)*arr[ind] + func(ind + 1, 1, cap, n, arr, dp));
        }
        
        // We can sell the stock
        if (buy == 1) { 
            profit = Math.max(0 + func(ind + 1, 1, cap, n, arr, dp), arr[ind] + func(ind + 1, 0, cap-1, n, arr, dp));
        }

        /* Store the value in dp array and
        return the calculated profit */
        return dp[ind][buy][cap] = profit;
    }

    // Function to calculate the maximum profit earned 
    public int stockBuySell(int[] arr, int n, int k) {
        if (n == 0) 
            return 0;
            
        // Declare a DP table to memoize results
        int[][][] dp = new int[n][2][k+1];
        
        // Initialize the dp array with -1
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < 2; j++) {
                Arrays.fill(dp[i][j], -1);
            }
        }

        int ans = func(0, 0, k, n, arr, dp);
        
        // Return the maximum profit
        return ans;
    }

    public static void main(String[] args) {
        int n = 8;
        int[] arr = {3, 3, 5, 0, 0, 3, 1, 4};
        int k = 3;
        
        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the stockBuySell function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(arr, n, k));
    }
}
class Solution:
    # Function to find maximum profit earned using memoization
    def func(self, ind, buy, cap, n, arr, dp):
        # Base case 
        if ind == n or cap == 0:
            return 0
            
        """ If the result for this state has 
        already been calculated, return it"""
        if dp[ind][buy][cap] != -1:
            return dp[ind][buy][cap]
        
        profit = 0
        
        # We can buy the stock
        if buy == 0:
            profit = max(0 + self.func(ind + 1, 0, cap, n, arr, dp), (-1)*arr[ind] + self.func(ind + 1, 1, cap, n, arr, dp))
        
        # We can sell the stock
        if buy == 1:
            profit = max(0 + self.func(ind + 1, 1, cap, n, arr, dp), arr[ind] + self.func(ind + 1, 0, cap-1, n, arr, dp))
        
        """ Store the value in dp array and
        return the calculated profit"""
        dp[ind][buy][cap] = profit
        return dp[ind][buy][cap]

    # Function to calculate the maximum profit earned 
    def stockBuySell(self, arr, n, k):
        if n == 0:
            return 0
            
        """ Declare a 3D DP table with dimensions 
        (n) x 2 x 3 and initialize it with -1 """
        dp = [[[-1 for _ in range(k+1)] for _ in range(2)] for _ in range(n)]

        ans = self.func(0, 0, k, n, arr, dp)
        
        # Return the maximum profit
        return ans

if __name__ == "__main__":
    n = 8
    arr = [3, 3, 5, 0, 0, 3, 1, 4]
    k = 3
    
    # Create an instance of Solution class
    sol = Solution()

    # Call the stockBuySell function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(arr, n, k))
class Solution {
    // Function to find maximum profit earned using memoization
    func(ind, buy, cap, n, arr, dp) {
        // Base case 
        if (ind === n || cap === 0) {
            return 0;
        }
        /* If the result for this state has 
        already been calculated, return it*/
        if (dp[ind][buy][cap] !== -1) {
            return dp[ind][buy][cap];
        }
        let profit = 0;
        
        // We can buy the stock
        if (buy === 0) { 
            profit = Math.max(0 + this.func(ind + 1, 0, cap, n, arr, dp), (-1)*arr[ind] + this.func(ind + 1, 1, cap, n, arr, dp));
        }
        
        // We can sell the stock
        if (buy === 1) { 
            profit = Math.max(0 + this.func(ind + 1, 1, cap, n, arr, dp), arr[ind] + this.func(ind + 1, 0, cap-1, n, arr, dp));
        }

        /* Store the value in dp array and
        return the calculated profit */
        dp[ind][buy][cap] = profit;
        return dp[ind][buy][cap];
    }

    // Function to calculate the maximum profit earned 
    stockBuySell(arr, n, k) {
        if (n === 0) 
            return 0;
            
        // Initialize a DP table to memoize results
        const dp = new Array(n).fill(null).map(() =>
            new Array(2).fill(null).map(() =>
                new Array(k+1).fill(-1)
            )
        );

        let ans = this.func(0, 0, k, n, arr, dp);
        
        // Return the maximum profit
        return ans;
    }
}
    const n = 8;
    const arr = [3, 3, 5, 0, 0, 3, 1, 4];
    const k = 3;
    
    // Create an instance of Solution class
    const sol = new Solution();

    // Call the stockBuySell function and print the result
    console.log("The maximum profit that can be generated is", sol.stockBuySell(arr, n, k));

Complexity Analysis:

Time Complexity: O(N*2*k), There are N*2*k states therefore at max ‘N*2*k’ new problems will be solved.

Space Complexity:O(N*2*k) + O(N), As we are using a recursion stack space(O(N)) and a 3D array ( O(N*2*k)).

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp array of size [n+1][2][k+1]: As there are three changing parameters in the recursive solution, 'ind', 'buy' and 'cap'. The maximum value 'ind' can attain is (n) and including 0 its n+1, where n is the size of array, for 'buy' only two values possible 0, 1 and lastly 'cap' can attain three values 0, to k as only 'k' transactions are possible as per the problem statement. So we need a 3D array and initialize the array as 0.

Setting Base Cases in the Array: In the recursive code, our base condition was when If ind == n, it means we have finished trading on all days, and there is no more money that we can get, therefore simply return 0. But here when n 'ind' = 0, 'cap' and 'buy' can take any value, therefore set two loops and initialize dp[n][buy][cap] = 0.

When cap == 0, the other two variables, 'ind' and 'cap' can take any value, therefore we set dp[ind][buy][0] = 0 usnig nested loops.

Iterative Computation Using Loops: As we have initialized the array as 0, we have automatically set the base condition as explained above. Now, traverse the array in the opposite direction of that of the memoization technique. We will start from 'ind' = n-1 and traverse till 'ind' =0. In every iteration do the same step as it was done in the recursive code logic.

Choosing the maximum: As we are looking to maximize the profit earned, return the maximum value in all the cases as discussed in memoization approach.

Returning the answer: At last dp[0][0][k] ( maximum profit generated on ith day, when we can buy the stock on 0th day and can have a total 'k' transactions) gives us the final answer.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to find the maximum profit using tabulation
    int func(vector<int>& arr, int n, int k) {
        
        /* Creating a 3D DP array of size 
        [n+1][2][k+1] initialized to 0*/
        vector<vector<vector<int>>> dp(n + 1, vector<vector<int>>(2, vector<int>(k+1, 0)));

        /* Base case: dp array is already initialized
        to 0, covering the base case.*/

        // Iterate backwards through the prices array
        for (int ind = n - 1; ind >= 0; ind--) {
            
            // buy can be 0 (buying) or 1 (selling)
            for (int buy = 0; buy <= 1; buy++) {
                
                /* cap represents the number of 
                transactions completed (can be 1 to k)*/
                for (int cap = 1; cap <= k; cap++) {
                    
                    // We can buy the stock
                    if (buy == 0) { 
                        dp[ind][buy][cap] = max(0 + dp[ind + 1][0][cap],
                                               (-1)*arr[ind] + dp[ind + 1][1][cap]);
                    }
                    // We can sell the stock
                    if (buy == 1) { 
                        dp[ind][buy][cap] = max(0 + dp[ind + 1][1][cap],
                                               arr[ind] + dp[ind + 1][0][cap - 1]);
                    }
                }
            }
        }

        /* The result is stored in dp[0][0][k] which
        represents maximum profit after final transaction.*/
        return dp[0][0][k];
    }
public:
    //Function to find the maximum profit
    int stockBuySell(vector<int> &arr, int n, int k){
        //Return the answer
        return func(arr, n, k);
    }
};

int main() {
    vector<int> prices = {3, 3, 5, 0, 0, 3, 1, 4};
    int n = prices.size();
    int k = 3;

    // Create an instance of the Solution class
    Solution sol; 
    
    // Call the function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(prices, n, k) << endl;

    return 0;
}
import java.util.*;

class Solution {
    // Function to find the maximum profit using tabulation
    private int func(int[] arr, int n, int k) {
        /* Declaring a 3D DP array of 
        size [n+1][2][k+1] initialized to 0*/
        int[][][] dp = new int[n + 1][2][k+1];

        /* Base case: dp array is already i
        nitialized to 0, covering the base case.*/

        // Iterate backwards through the prices array
        for (int ind = n - 1; ind >= 0; ind--) {
            
            // buy can be 0 (buying) or 1 (selling)
            for (int buy = 0; buy <= 1; buy++) {
                
                /* cap represents the number of 
                transactions completed (can be 1 to k)*/
                for (int cap = 1; cap <= k; cap++) {
                    // We can buy the stock
                    if (buy == 0) { 
                        dp[ind][buy][cap] = Math.max(0 + dp[ind + 1][0][cap],
                                                     (-1)*arr[ind] + dp[ind + 1][1][cap]);
                    }
                    // We can sell the stock
                    if (buy == 1) { 
                        dp[ind][buy][cap] = Math.max(0 + dp[ind + 1][1][cap],
                                                     arr[ind] + dp[ind + 1][0][cap - 1]);
                    }
                }
            }
        }

        /* The result is stored in dp[0][0][k] which
        represents maximum profit after the final transaction.*/
        return dp[0][0][k];
    }

    // Function to find the maximum profit
    public int stockBuySell(int[] arr, int n, int k) {
        // Return the answer
        return func(arr, n, k);
    }

    public static void main(String[] args) {
        int[] prices = {3, 3, 5, 0, 0, 3, 1, 4};
        int n = prices.length;
        int k = 3;

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Call the function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(prices, n, k));
    }
}
class Solution:
    # Function to find the maximum profit using tabulation
    def func(self, arr, n, k):
        """ Declaring a 3D DP array of size 
        [n+1][2][k+1] initialized to 0"""
        dp = [[[0 for _ in range(k+1)] for _ in range(2)] for _ in range(n + 1)]

        """ Base case: dp array is already 
        initialized to 0, covering the base case."""

        # Iterate backwards through the prices array
        for ind in range(n - 1, -1, -1):
            
            # buy can be 0 (buying) or 1 (selling)
            for buy in range(2):
                
                """ cap represents the number of 
                transactions completed (can be 1 to k)"""
                for cap in range(1, k+1):
                    # We can buy the stock
                    if buy == 0:
                        dp[ind][buy][cap] = max(0 + dp[ind + 1][0][cap],
                                                (-1)*arr[ind] + dp[ind + 1][1][cap])
                    # We can sell the stock
                    if buy == 1:
                        dp[ind][buy][cap] = max(0 + dp[ind + 1][1][cap],
                                                arr[ind] + dp[ind + 1][0][cap - 1])

        """ The result is stored in dp[0][0][k] which 
        represents maximum profit after the final transaction."""
        return dp[0][0][k]

    # Function to find the maximum profit
    def stockBuySell(self, arr, n, k):
        # Return the answer
        return self.func(arr, n, k)

if __name__ == "__main__":
    prices = [3, 3, 5, 0, 0, 3, 1, 4]
    n = len(prices)
    k = 3

    # Create an instance of the Solution class
    sol = Solution()

    # Call the function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(prices, n, k))
class Solution {
    // Function to find the maximum profit using tabulation
    func(arr, n, k) {
        /* Declaring a 3D DP array of size
        [n+1][2][k+1] initialized to 0*/
        let dp = new Array(n + 1).fill().map(() => new Array(2).fill().map(() => new Array(k+1).fill(0)));

        /* Base case: dp array is already 
        initialized to 0, covering the base case.*/

        // Iterate backwards through the prices array
        for (let ind = n - 1; ind >= 0; ind--) {
            // buy can be 0 (buying) or 1 (selling)
            
            for (let buy = 0; buy <= 1; buy++) {
                
                /* cap represents the number of 
                transactions completed (can be 1 to k)*/
                for (let cap = 1; cap <= k; cap++) {
                    // We can buy the stock
                    if (buy === 0) { 
                        dp[ind][buy][cap] = Math.max(0 + dp[ind + 1][0][cap],
                                                     (-1)*arr[ind] + dp[ind + 1][1][cap]);
                    }
                    // We can sell the stock
                    if (buy === 1) { 
                        dp[ind][buy][cap] = Math.max(0 + dp[ind + 1][1][cap],
                                                     arr[ind] + dp[ind + 1][0][cap - 1]);
                    }
                }
            }
        }

        /* The result is stored in dp[0][0][k] which
        represents maximum profit after the final transaction.*/
        return dp[0][0][k];
    }

    // Function to find the maximum profit
    stockBuySell(arr, n, k) {
        
        // Return the answer
        return this.func(arr, n, k);
    }
}

let prices = [3, 3, 5, 0, 0, 3, 1, 4];
let n = prices.length;
let k = 3;

// Create an instance of the Solution class
let sol = new Solution();

// Call the function and print the result
console.log("The maximum profit that can be generated is " + sol.stockBuySell(prices, n, k));

Complexity Analysis:

Time Complexity: O(N*2*k), As, here are three nested loops that account for O(N*2*k) complexity.

Space Complexity:O(N*2*k), As a 3D array of size N*2*k is used.

If we observe the relation obtained in the tabulation, dp[ind][buy][cap] = max( dp[ind+1][buy][cap] , max( dp[ind+1][!buy][cap]), We see that to calculate a value of a cell of the dp array, we need only the next row values(say ahead of ind+1). So, we don’t need to store an entire 2-D array. Hence we can space optimize it.

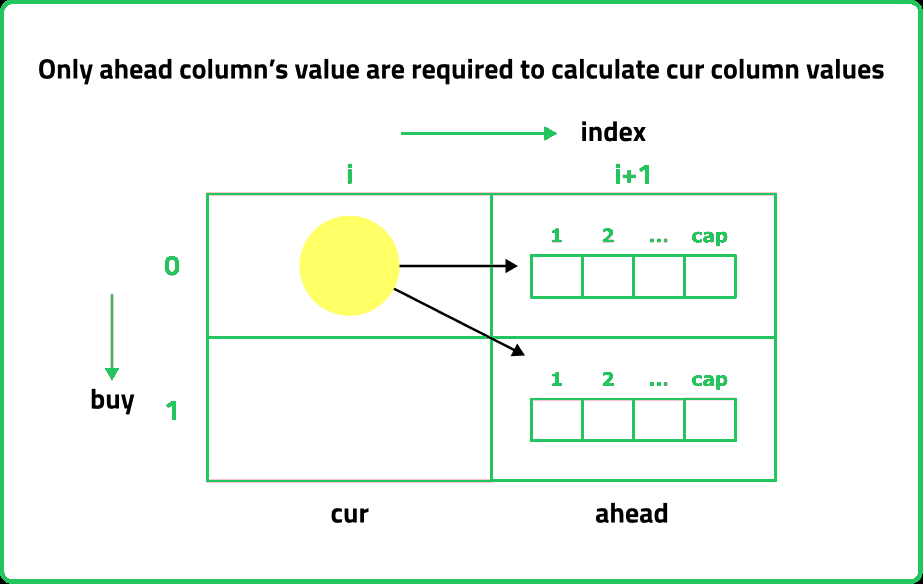
The Steps to space optimize the tabulation approach are as follows:

Declare a 2D vector 'ahead' initialized to 0 (base condition) and another 2D vector 'cur' also set to 0.

Then initialize three nested loops to calculate the 'cur' array’s values. Replace dp[ind] with 'cur' and dp[ind+1] with ahead in our tabulation code.

After the inner loop execution, set 'ahead' as 'cur' for the next outer loop iteration. At last, return ahead[0][k] as our answer.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /*Function to find our maximum 
    profit using space optimization*/
    int func(vector<int>& arr, int n, int k) {
        /* Create two 2D arrays to store profit information,
        one for current state and one for the ahead state.*/
        vector<vector<int>> ahead(2, vector<int>(k+1, 0));
        vector<vector<int>> cur(2, vector<int>(k+1, 0));

        // Iterate backwards through the prices array
        for (int ind = n - 1; ind >= 0; ind--) {
            
            // buy can be 0 (buying) or 1 (selling)
            for (int buy = 0; buy <= 1; buy++) {
                
                /* cap represents the number of 
                transactions completed (can be 1 or 2)*/
                for (int cap = 1; cap <= k; cap++) {
                    // We can buy the stock
                    if (buy == 0) { 
                        cur[buy][cap] = max(0 + ahead[0][cap], 
                                            -arr[ind] + ahead[1][cap]);
                    }
                    // We can sell the stock
                    if (buy == 1) { 
                        cur[buy][cap] = max(0 + ahead[1][cap],
                                            arr[ind] + ahead[0][cap - 1]);
                    }
                }
            }
            /* Update the ahead state with the
            current state for the next iteration*/
            ahead = cur;
        }

        /* Return the maximum profit after completing
        k transactions starting from index 0.*/
        return ahead[0][k];
    }
public:
    //Function to find out maximum profit
    int stockBuySell(vector<int> &arr, int n, int k){
        //Return the answer
        return func(arr, n, k);
    }
};

int main() {
    vector<int> prices = {3, 3, 5, 0, 0, 3, 1, 4};
    int n = prices.size();
    int k = 3;

    // Create an instance of the Solution class
    Solution sol;

    // Call the funntion and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(prices, n, k) << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find our maximum 
    profit using space optimization*/
    private int func(int[] arr, int n, int k) {
        /* Create two 2D arrays to store profit information,
        one for current state and one for the ahead state.*/
        int[][] ahead = new int[2][k+1];
        int[][] cur = new int[2][k+1];

        // Iterate backwards through the prices array
        for (int ind = n - 1; ind >= 0; ind--) {
            
            // buy can be 0 (buying) or 1 (selling)
            for (int buy = 0; buy <= 1; buy++) {
                
                /* cap represents the number of 
                transactions completed (can be 1 or 2)*/
                for (int cap = 1; cap <= k; cap++) {
                    // We can buy the stock
                    if (buy == 0) {
                        cur[buy][cap] = Math.max(0 + ahead[0][cap],
                                                 (-1)*arr[ind] + ahead[1][cap]);
                    }
                    // We can sell the stock
                    if (buy == 1) {
                        cur[buy][cap] = Math.max(0 + ahead[1][cap],
                                                 arr[ind] + ahead[0][cap - 1]);
                    }
                }
            }
            /* Update the ahead state with the 
            current state for the next iteration*/
            ahead = cur;
        }

        /* Return the maximum profit after completing
        k transactions starting from index 0*/
        return ahead[0][k];
    }

    // Function to find out maximum profit
    public int stockBuySell(int[] arr, int n, int k) {
        // Return the answer
        return func(arr, n, k);
    }

    public static void main(String[] args) {
        int[] prices = {3, 3, 5, 0, 0, 3, 1, 4};
        int n = prices.length;
        int k = 3;

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Call the function and print the result
        System.out.println("The maximum profit that can be generated is " + sol.stockBuySell(prices, n, k));
    }
}
class Solution:
    """ Function to find our maximum 
    profit using space optimization"""
    def func(self, arr, n, k):
        """ Create two 2D arrays to store profit information,
        one for current state and one for the ahead state."""
        ahead = [[0] * (k+1) for _ in range(2)]
        cur = [[0] * (k+1) for _ in range(2)]

        # Iterate backwards through the prices array
        for ind in range(n - 1, -1, -1):
            
            # buy can be 0 (buying) or 1 (selling)
            for buy in range(2):
                
                """ cap represents the number of 
                transactions completed (can be 1 or 2)"""
                for cap in range(1, k+1):
                    # We can buy the stock
                    if buy == 0:
                        cur[buy][cap] = max(0 + ahead[0][cap],
                                            -arr[ind] + ahead[1][cap])
                    # We can sell the stock
                    if buy == 1:
                        cur[buy][cap] = max(0 + ahead[1][cap],
                                            arr[ind] + ahead[0][cap - 1])
            """ Update the ahead state with the 
            current state for the next iteration"""
            ahead = [row[:] for row in cur]

        """ Return the maximum profit after completing 
        k transactions starting from index 0"""
        return ahead[0][k]

    # Function to find out maximum profit
    def stockBuySell(self, arr, n, k):
        # Return the answer
        return self.func(arr, n, k)

if __name__ == "__main__":
    prices = [3, 3, 5, 0, 0, 3, 1, 4]
    n = len(prices)
    k = 3

    # Create an instance of the Solution class
    sol = Solution()

    # Call the function and print the result
    print("The maximum profit that can be generated is", sol.stockBuySell(prices, n, k))
class Solution {
    /* Function to find our maximum 
    profit using space optimization*/
    func(arr, n, k) {
        /* Create two 2D arrays to store profit information,
        one for current state and one for the ahead state.*/
        let ahead = Array.from({ length: 2 }, () => Array(k+1).fill(0));
        let cur = Array.from({ length: 2 }, () => Array(k+1).fill(0));

        // Iterate backwards through the prices array
        for (let ind = n - 1; ind >= 0; ind--) {
            
            // buy can be 0 (buying) or 1 (selling)
            for (let buy = 0; buy <= 1; buy++) {
                
                /* cap represents the number of 
                transactions completed (can be 1 or 2)*/
                for (let cap = 1; cap <= k; cap++) {
                    // We can buy the stock
                    if (buy === 0) {
                        cur[buy][cap] = Math.max(0 + ahead[0][cap],
                                                 -arr[ind] + ahead[1][cap]);
                    }
                    // We can sell the stock
                    if (buy == 1) {
                        cur[buy][cap] = Math.max(0 + ahead[1][cap],
                                                 arr[ind] + ahead[0][cap - 1]);
                    }
                }
            }
            /* Update the ahead state with the 
            current state for the next iteration*/
            ahead = cur;
        }

        /* Return the maximum profit after completing
        k transactions starting from index 0*/
        return ahead[0][k];
    }

    // Function to find out maximum profit
    stockBuySell(arr, n, k) {
        // Return the answer
        return this.func(arr, n, k);
    }
}
let prices = [3, 3, 5, 0, 0, 3, 1, 4];
let n = prices.length;
let k = 3;

// Create an instance of the Solution class
let sol = new Solution();

// Call the function and print the result
console.log("The maximum profit that can be generated is " + sol.stockBuySell(prices, n, k));

Complexity Analysis:

Time Complexity: O(N*2*k), As, here are three nested loops that account for O(N*2*k) complexity.

Space Complexity:O(1), As we are using two external arrays of size ‘2*k’.

Problem List

Best time to buy and sell stock IV

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

The Steps to space optimize the tabulation approach are as follows:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code