Find Nth root of a number
Binary Search
On answers
Medium
- This concept is widely used in game development, 3D graphics and image manipulation software
- It's a key part in calculating distances and generating effects such as fog or light falloff
- Additionally, the problem comes into play in audio processing for generating specific tones or adjusting volume and pitch
- This mathematical operation, finding the Nth root, is an integral part of many algorithmic solutions in software
Given two numbers N and M, find the Nth root of M. The Nth root of a number M is defined as a number X such that when X is raised to the power of N, it equals M. If the Nth root is not an integer, return -1.
Examples:
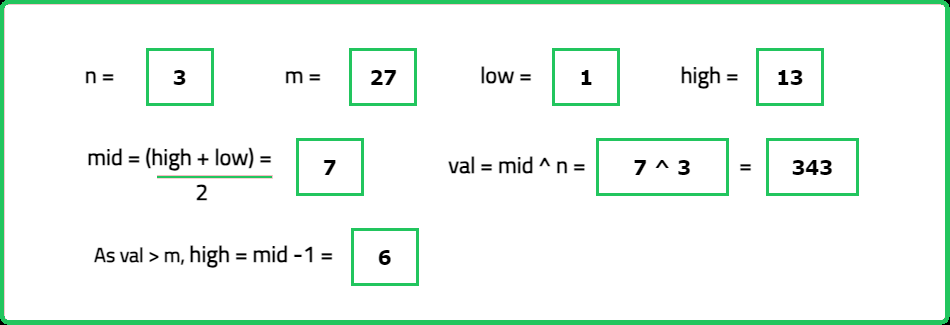
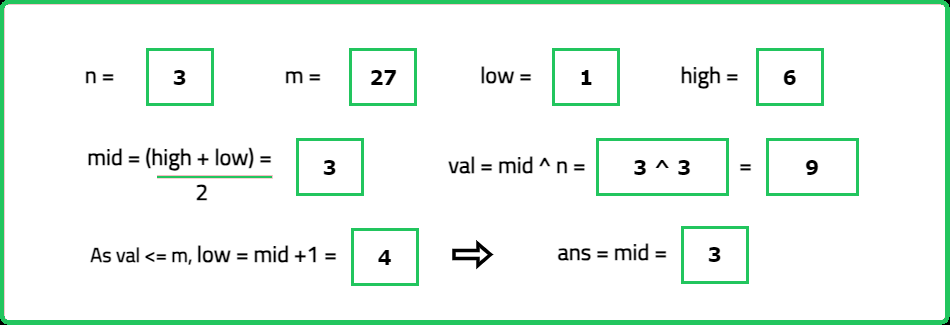
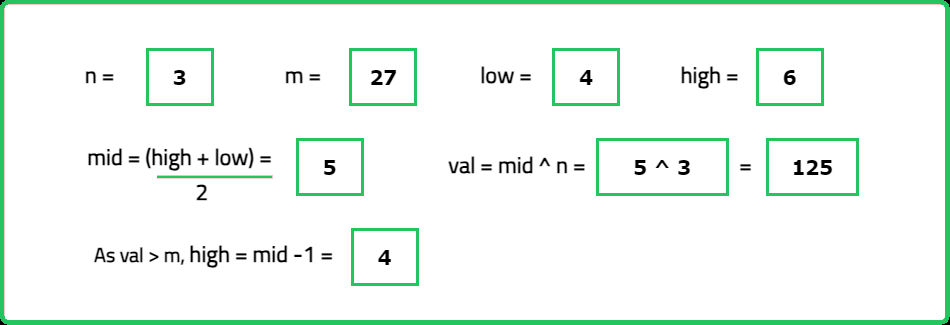
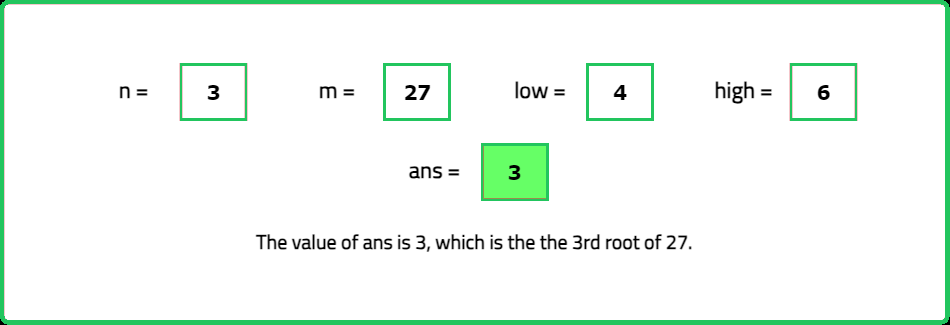
Input: N = 3, M = 27
Output: 3
Explanation: The cube root of 27 is equal to 3.
Input: N = 4, M = 69
Output:-1
Explanation: The 4th root of 69 does not exist. So, the answer is -1.
Input: N = 4, M = 81
Constraints
- 1 <= N <= 30
- 1 <= M <= 109
Hints
- The N-th root of M is a number X such that X^N=M. The goal is to find X, and if X is not an integer, return −1. This problem involves numerical precision and logical decision-making to determine if X is an integer.
- "Use binary search to find X in the range [1,M]: Compute mid^N at each step."
Company Tags
Swiggy
DoorDash
American Express
Morgan Stanley
Broadcom
Stripe
Qualcomm
Rockstar Games
Micron Technology
Riot Games
Splunk
Bungie
Pinterest
Philips Healthcare
Nutanix
Salesforce
PayPal
Visa
Lyft
Target
OYO Rooms
Epic Systems
Shopify
Goldman Sachs
McKinsey & Company
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro