First and last occurrence
Binary Search
Logic Building
Easy
- Fun Fact: This problem is essentially about range queries which are a very common task in database management systems and search engines
- For instance, if you use the filter function in an e-commerce website to specify a price range for a product, you're effectively asking the database to perform an operation much like this problem
- The database will search through its sorted data to find the starting and ending positions of all products that fall within your specified price range
- So the next time you're shopping online, remember you're indirectly solving this problem!
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value. If the target is not found in the array, return [-1, -1].
Examples:
Input: nums = [5, 7, 7, 8, 8, 10], target = 8
Output: [3, 4]
Explanation:The target is 8, and it appears in the array at indices 3 and 4, so the output is [3,4]
Input: nums = [5, 7, 7, 8, 8, 10], target = 6
Output: [-1, -1]
Expalantion: The target is 6, which is not present in the array. Therefore, the output is [-1, -1].
Input: nums = [5, 7, 7, 8, 8, 10], target = 5
Constraints
- 0 <= nums.length <= 105
- -109 <= nums[i] <= 109
- nums is a non-decreasing array.
- -109 <= target <= 109
Hints
- "Perform two separate binary searches: One to find the first occurrence of the target. Another to find the last occurrence of the target."
- "To find the first occurrence, move the search to the left half even after finding the target. To find the last occurrence, move the search to the right half after finding the target."
Company Tags
PayPal
Qualcomm
Zoho
Western Digital
Johnson & Johnson
Ernst & Young
Roblox
eBay
Walmart
Shopify
Deloitte
NVIDIA
Goldman Sachs
MongoDB
Etsy
Dropbox
Riot Games
Flipkart
Bain & Company
Freshworks
Boston Consulting Group
Philips Healthcare
IBM
Roche
Robinhood
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro
Editorial
Intuition
The naive approach to solve this problem would be a linear traversal of the given array. We traverse the array and store the index where the target appears the first time, in both the first and last occurrence variables. We update the last variable when we again encounter an index where value is equal to the target.
Approach
- Declare two variables,
firstandlast, initialized to -1 to store the first and last occurrences of the target value. - Traverse the array, when the target value is first encountered in the array, store the index in both
firstandlast. - For subsequent occurrences of the target value, update only the
lastvariable with the current index. - Store the first and last occurrences in a vector and return that vector as a result.
Dry Run: Please refer to the video for the dry-run.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
// Initialize variables to store first and last occurrences
int first = -1, last = -1;
vector<int> ans;
// Iterate through the array
for (int i = 0; i < nums.size(); i++) {
// Check if current element is the target
if (nums[i] == target) {
if (first == -1) first = i;
last = i;
}
}
// Store the results in the answer vector
ans.push_back(first);
ans.push_back(last);
return ans;
}
};
int main()
{
vector<int> nums = {5, 7, 7, 8, 8, 10};
int target = 8;
// Create an instance of the Solution class
Solution sol;
// Function call to find the first and last occurrences
vector<int> result = sol.searchRange(nums, target);
cout << "The first and last occurrences are at indices: "
<< result[0] << " and " << result[1] << "\n";
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839
import java.util.*;
class Solution {
public int[] searchRange(int[] nums, int target) {
// Initialize variables to store first and last occurrences
int first = -1, last = -1;
int[] ans = new int[2];
// Iterate through the array
for (int i = 0; i < nums.length; i++) {
// Check if current element is the target
if (nums[i] == target) {
if (first == -1) first = i;
last = i;
}
}
// Store the results in the answer array
ans[0] = first;
ans[1] = last;
return ans;
}
public static void main(String[] args) {
int[] nums = {5, 7, 7, 8, 8, 10};
int target = 8;
// Create an instance of the Solution class
Solution sol = new Solution();
// Function call to find the first and last occurrences
int[] result = sol.searchRange(nums, target);
System.out.println("The first and last occurrences are at indices: "
+ result[0] + " and " + result[1]);
}
}
123456789101112131415161718192021222324252627282930
class Solution:
def searchRange(self, nums, target):
# Initialize variables to store first and last occurrences
first, last = -1, -1
# Iterate through the array
for i in range(len(nums)):
# Check if current element is the target
if nums[i] == target:
if first == -1:
first = i
last = i
# Return the results as a list
return [first, last]
# Example usage
if __name__ == "__main__":
nums = [5, 7, 7, 8, 8, 10]
target = 8
# Create an instance of the Solution class
sol = Solution()
# Function call to find the first and last occurrences
result = sol.searchRange(nums, target)
print(f"The first and last occurrences are at indices: {result[0]} and {result[1]}")
123456789101112131415161718192021222324252627282930313233
class Solution {
searchRange(nums, target) {
// Initialize variables to store first and last occurrences
let first = -1, last = -1;
// Iterate through the array
for (let i = 0; i < nums.length; i++) {
// Check if current element is the target
if (nums[i] === target) {
if (first === -1)
first = i;
last = i;
}
}
// Return the results as an array
return [first, last];
}
}
// Example usage
const nums = [5, 7, 7, 8, 8, 10];
const target = 8;
// Create an instance of the Solution class
const sol = new Solution();
// Function call to find the first and last occurrences
const result = sol.searchRange(nums, target);
console.log(`The first and last occurrences are at indices: ${result[0]} and ${result[1]}`);
Complexity Analysis:
Time Complexity: O(N), where N is the size of the given array. This is because we are performing a linear search through the array to find the first and last occurrences of the target element.
Space Complexity: O(1), as we are not using any extra space that grows with the input size. We are only using a few additional variables to store indices and results.
Intuition
In this approach, we use the lower bound and upper bound values to get the first and last occurrences of the target element. Lower bound of the target element will provide us index of the first occurrence of the target element. And, upper bound will provide the index of the element just after the last appearance of the target. So, we could return the lower bound and the upper bound - 1, as the first and last occurrences of the target in the given array.
Approach
-
For Lower Bound:
- To get the lower bound, use low and high pointers(Binary search approach) initialized with first and last indices.
- Calculate the middle element and compare the values as mentioned in the below two points.
- If the middle element is greater than or equal to target, update it as our possible answer and eliminate the right half by decreasing the high pointer.
- If the middle element is lesser than the target, eliminate the left half.
- Keep following these steps till the low pointer lesser than or equal to the high pointer.
- To get the upper bound, use low and high pointers(Binary search approach initialized with first and last indices.
- Then calculate the middle element and compare the values as mentioned in the below two points.
- If the middle element is greater than target, store it as our possible answer and eliminate the right half by decreasing the high pointer.
- If the middle element is lesser than or equal to target, eliminate the left half.
- Keep following these steps till the low pointer lesser than or equal to the high pointer.
- Edge Case: In case the lower bound is equal to the size of the array or the value of array at index = lower bound is not equal to the target element, return both the first and last occurrence as -1. As it means that the target is not present in the array.
- Now return the lower bound and (upper bound - 1) as the first and last occurrences of the target element in the given array.
For Upper Bound:
Dry Run: Please refer to the video for the dry-run.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192
#include <bits/stdc++.h>
using namespace std;
class Solution
{
private:
// Function to find the lower bound of the target
int lowerBound(vector<int> &nums, int target) {
int low = 0, high = nums.size() - 1;
int ans = nums.size();
// Applying binary search algorithm
while(low <= high) {
int mid = (low + high) / 2;
/* If the middle element is greater than
or equal to the target element update
the answer as mid and eliminate the right half */
if(nums[mid] >= target) {
ans = mid;
high = mid - 1;
}
/* If the middle element is smaller than
the target element then we eliminate
the left half */
else {
low = mid + 1;
}
}
return ans;
}
// Function to find the upper bound of the target
int upperBound(vector<int> &nums, int target) {
int low = 0, high = nums.size() - 1;
int ans = nums.size();
// Applying binary search algorithm
while(low <= high) {
int mid = (low + high) / 2;
/* If the middle element is greater than
the target element update the answer
as mid and eliminate the right half */
if(nums[mid] > target) {
ans = mid;
high = mid - 1;
}
/* If the middle element is greater than
or equal to the target element
eliminate the right half */
else {
low = mid + 1;
}
}
return ans;
}
public:
// Function to find the first and last occurrences of the target
vector<int> searchRange(vector<int> &nums, int target) {
// Function call to find the first occurrence (lower bound)
int firstOcc = lowerBound(nums, target);
// Check if the target is present in the array or not
if(firstOcc == nums.size() || nums[firstOcc] != target) return {-1, -1};
// Function call to find the last occurrence (upper bound)
int lastOcc = upperBound(nums, target) - 1;
return {firstOcc, lastOcc};
}
};
int main()
{
vector<int> nums = {5, 7, 7, 8, 8, 10};
int target = 8;
// Create an instance of the Solution class
Solution sol;
// Function call to find the first and last occurrences
vector<int> result = sol.searchRange(nums, target);
cout << "The first and last occurrences are at indices: "
<< result[0] << " and " << result[1] << "\n";
return 0;
}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182
import java.util.*;
class Solution {
private int lowerBound(int[] nums, int target) {
int low = 0, high = nums.length - 1;
int ans = nums.length;
// Applying binary search algorithm
while(low <= high) {
int mid = (low + high) / 2;
/* If the middle element is greater than
or equal to the target element update
the answer as mid and eliminate the right half */
if(nums[mid] >= target) {
ans = mid;
high = mid - 1;
}
/* If the middle element is smaller than
the target element then we eliminate
the left half */
else {
low = mid + 1;
}
}
return ans;
}
private int upperBound(int[] nums, int target) {
int low = 0, high = nums.length - 1;
int ans = nums.length;
// Applying binary search algorithm
while(low <= high) {
int mid = (low + high) / 2;
/* If the middle element is greater than
the target element update the answer
as mid and eliminate the right half */
if(nums[mid] > target) {
ans = mid;
high = mid - 1;
}
/* If the middle element is greater than
or equal to the target element
eliminate the right half */
else {
low = mid + 1;
}
}
return ans;
}
public int[] searchRange(int[] nums, int target) {
// Function call to find the first occurrence (lower bound)
int firstOcc = lowerBound(nums, target);
// Check if the target is present in the array or not
if(firstOcc == nums.length || nums[firstOcc] != target) return new int[]{-1, -1};
// Function call to find the last occurrence (upper bound)
int lastOcc = upperBound(nums, target) - 1;
return new int[]{firstOcc, lastOcc};
}
public static void main(String[] args) {
int[] nums = {5, 7, 7, 8, 8, 10};
int target = 8;
// Create an instance of the Solution class
Solution sol = new Solution();
// Function call to find the first and last occurrences
int[] result = sol.searchRange(nums, target);
System.out.println("The first and last occurrences are at indices: "
+ result[0] + " and " + result[1]);
}
}123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
class Solution:
def lowerBound(self, nums, target):
low, high = 0, len(nums) - 1
ans = len(nums)
# Applying binary search algorithm
while low <= high:
mid = (low + high) // 2
# If the middle element is greater than
# or equal to the target element update
# the answer as mid and eliminate the right half
if nums[mid] >= target:
ans = mid
high = mid - 1
# If the middle element is smaller than
# the target element then we eliminate
# the left half
else:
low = mid + 1
return ans
def upperBound(self, nums, target):
low, high = 0, len(nums) - 1
ans = len(nums)
# Applying binary search algorithm
while low <= high:
mid = (low + high) // 2
# If the middle element is greater than
# the target element update the answer
# as mid and eliminate the right half
if nums[mid] > target:
ans = mid
high = mid - 1
# If the middle element is greater than
# or equal to the target element
# eliminate the right half
else:
low = mid + 1
return ans
def searchRange(self, nums, target):
# Function call to find the first occurrence (lower bound)
firstOcc = self.lowerBound(nums, target)
# Check if the target is present in the array or not
if firstOcc == len(nums) or nums[firstOcc] != target:
return [-1, -1]
# Function call to find the last occurrence (upper bound)
lastOcc = self.upperBound(nums, target) - 1
return [firstOcc, lastOcc]
if __name__ == "__main__":
nums = [5, 7, 7, 8, 8, 10]
target = 8
# Create an instance of the Solution class
sol = Solution()
# Function call to find the first and last occurrences
result = sol.searchRange(nums, target)
print("The first and last occurrences are at indices:", result[0], "and", result[1])12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879
class Solution {
// Function to find the lower bound of the target
lowerBound(nums, target) {
let low = 0, high = nums.length - 1;
let ans = nums.length;
// Applying binary search algorithm
while(low <= high) {
let mid = Math.floor((low + high) / 2);
/* If the middle element is greater than
or equal to the target element update
the answer as mid and eliminate the right half */
if(nums[mid] >= target) {
ans = mid;
high = mid - 1;
}
/* If the middle element is smaller than
the target element then we eliminate
the left half */
else {
low = mid + 1;
}
}
return ans;
}
// Function to find the upper bound of the target
upperBound(nums, target) {
let low = 0, high = nums.length - 1;
let ans = nums.length;
// Applying binary search algorithm
while(low <= high) {
let mid = Math.floor((low + high) / 2);
/* If the middle element is greater than
the target element update the answer
as mid and eliminate the right half */
if(nums[mid] > target) {
ans = mid;
high = mid - 1;
}
/* If the middle element is greater than
or equal to the target element
eliminate the right half */
else {
low = mid + 1;
}
}
return ans;
}
// Function to find the first and last occurrences of the target
searchRange(nums, target) {
// Function call to find the first occurrence (lower bound)
let firstOcc = this.lowerBound(nums, target);
// Check if the target is present in the array or not
if(firstOcc == nums.length || nums[firstOcc] != target) return [-1, -1];
// Function call to find the last occurrence (upper bound)
let lastOcc = this.upperBound(nums, target) - 1;
return [firstOcc, lastOcc];
}
}
let nums = [5, 7, 7, 8, 8, 10];
let target = 8;
// Create an instance of the Solution class
let sol = new Solution();
// Function call to find the first and last occurrences
let result = sol.searchRange(nums, target);
console.log("The first and last occurrences are at indices:", result[0], "and", result[1]);Complexity Analysis:
Time Complexity: 2*O(log N), where N is the size of the given array. Both the lowerBound and upperBound functions perform a binary search, which operates in logarithmic time. Thus, the overall time complexity is O(log N).
Space Complexity: O(1), as we are using a constant amount of extra space regardless of the input size. The space used by the variables low, high, mid, and ans does not depend on the size of the input array.
Intuition
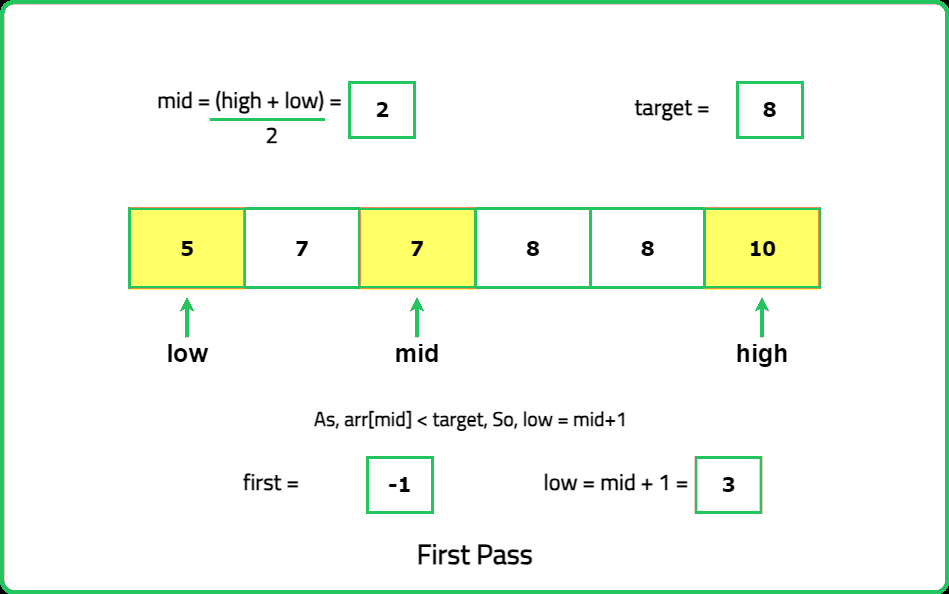
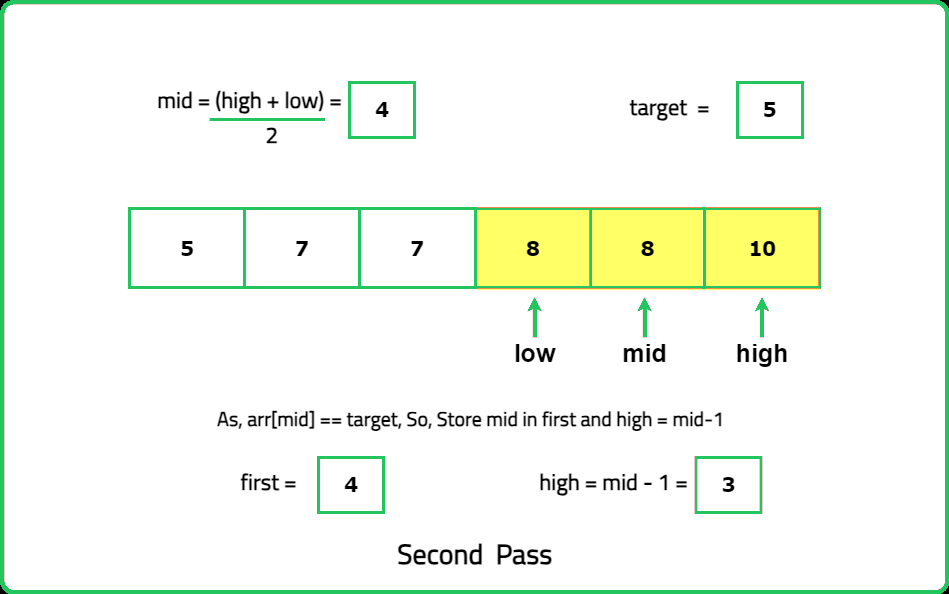
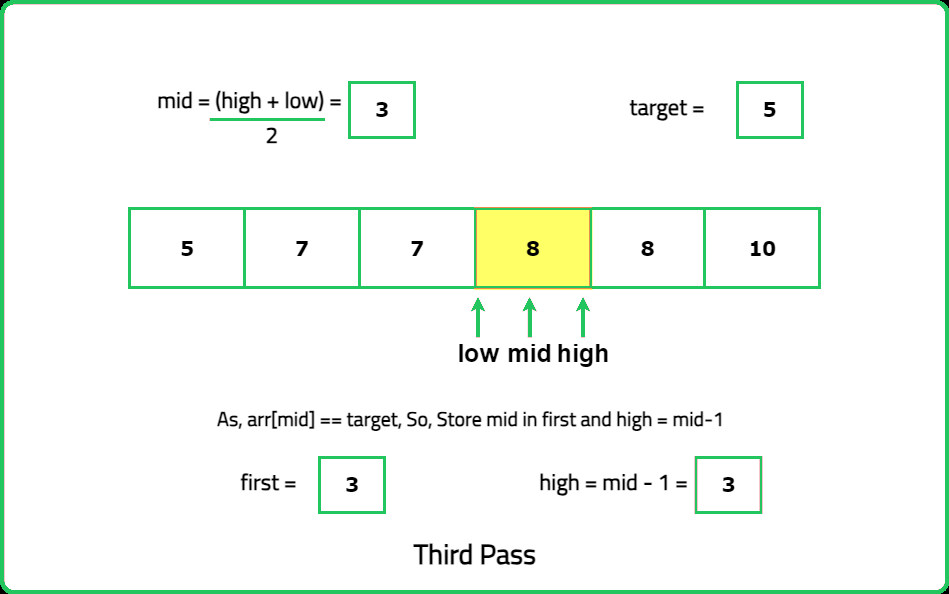
The optimal solution of this problem uses binary search to look for the first and last occurrences of the target element. While calculating the first occurrence, keep in mind that every time we get an element equal to target, look for the target again in its left half. Similarly, for getting the last occurrence, keep in mind that when we get an element equal to target, we look for the target again in its right half, so we get the last index where the target appears.
Approach
-
For firstOccurrence():
- Start with taking low and high pointers initialized with the first index, and last index as that would be the search space.
- Calculate the middle element and compare the values as mentioned in the below three points.
- If the middle element of array is equal to target, update it as an possible answer and eliminate the right half by decreasing the high pointer. Then, search in the left half for more smaller index that satisfies the same condition.
- If the middle element is lesser than the target, eliminate the left half.
- If the middle element is greater than the target, eliminate the right half.
- Keep following these steps till the low pointer lesser than or equal to the high pointer.
- Start with taking low and high pointers initialized with the first index, and last index.
- Calculate the middle element and compare the values as mentioned in the below three points.
- If the middle element of the array is equal to target, update it as a possible answer and eliminate the right half by decreasing the high pointer. Then, search in the right half for more greater index that satisfies the same condition.
- If the middle element is lesser than the target, eliminate the left half.
- If the middle element is greater than the target, eliminate the right half.
- Keep following these steps till the low pointer lesser than or equal to the high pointer.
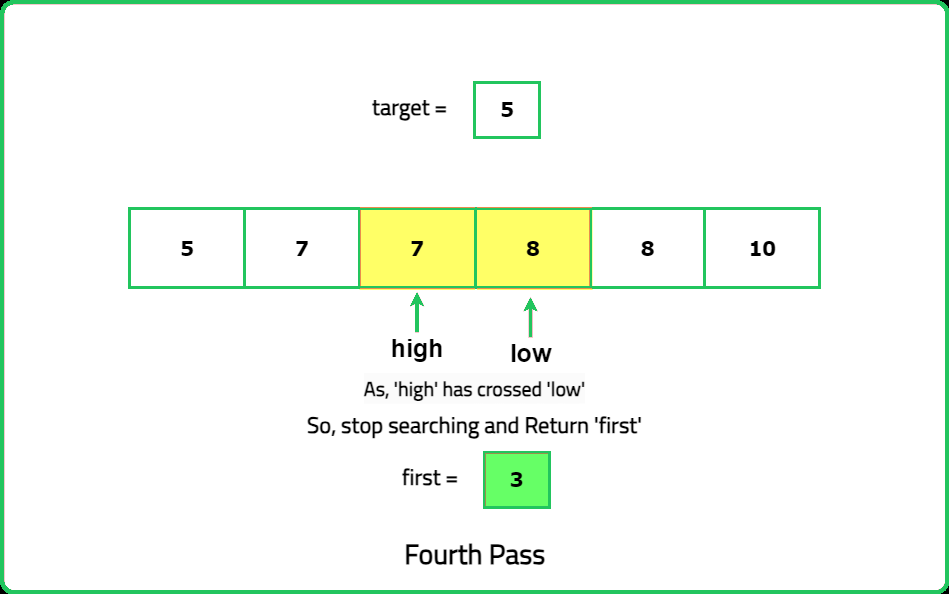
- Edge Case: In case the function firstOccurrence() returns -1, it'll indicate that the target element is not found in the array. If this happens we can directly return {-1,-1} as the answer. There would be no further need to calculate the last occurrence of the target element.
- Now return the lower bound and (upper bound - 1) as the first and last occurrences of the target element in the given array.
For lastOccurrence():
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105
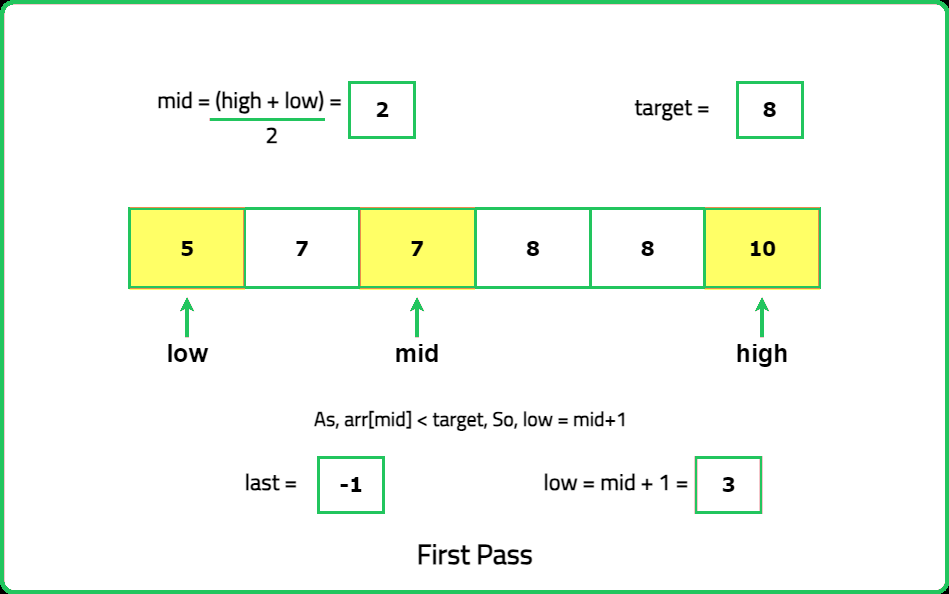
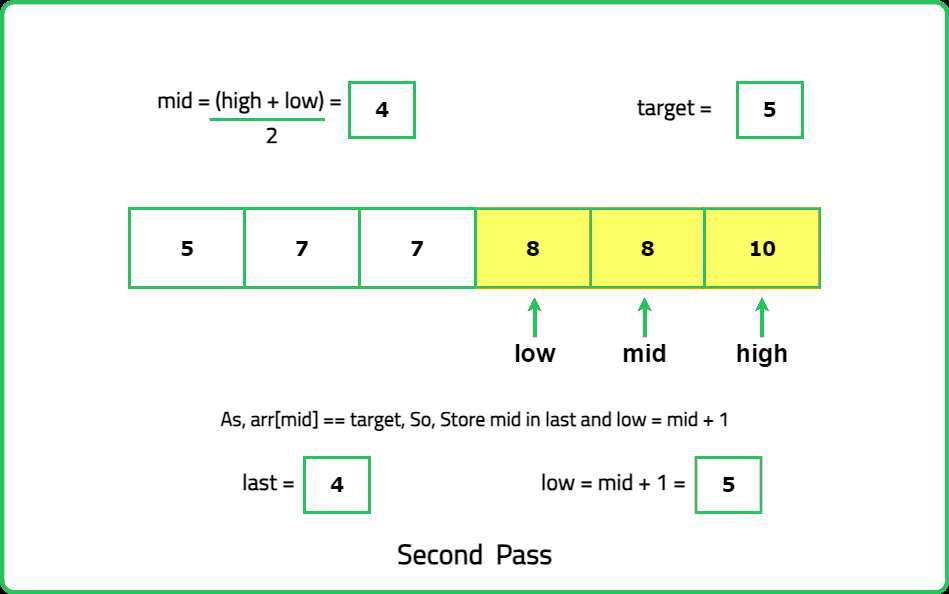
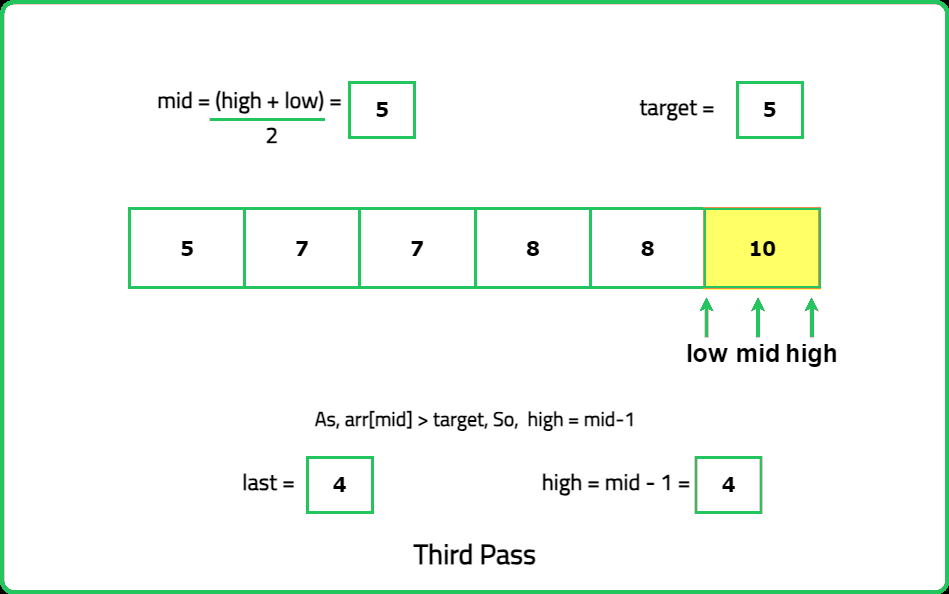
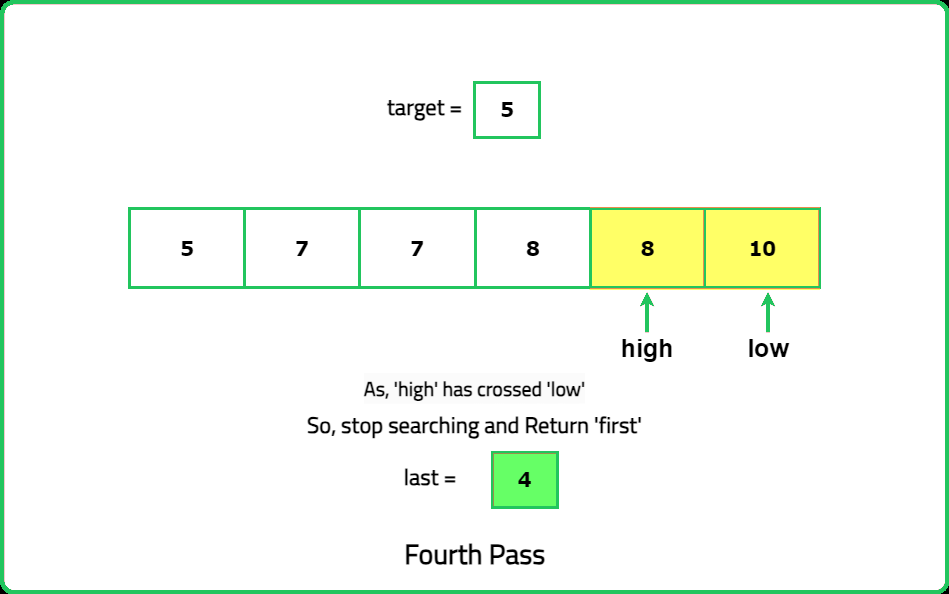
#include <bits/stdc++.h>
using namespace std;
class Solution
{
private:
// Function to find the first occurrence of the target
int firstOccurrence(vector<int> &nums, int target) {
int low = 0, high = nums.size() - 1;
int first = -1;
// Applying Binary Search Algorithm
while(low <= high) {
int mid = low + (high - low) / 2;
/* If the target element is found, we
update the first variable to mid and
eliminate the right half to look for
more smaller index where target is present */
if(nums[mid] == target) {
first = mid;
high = mid - 1;
}
/* If middle element is smaller,
we eliminate the left half */
else if(nums[mid] < target) {
low = mid + 1;
}
/* If middle element is greater,
we eliminate the right half */
else {
high = mid - 1;
}
}
return first;
}
// Function to find the last occurrence of the target
int lastOccurrence(vector<int> &nums, int target) {
int low = 0, high = nums.size() - 1;
int last = -1;
// Applying Binary Search Algorithm
while(low <= high) {
int mid = low + (high - low) / 2;
/* If the target element is found, we
update the first variable to mid and
eliminate the right half to look for
more greater index where target is present */
if(nums[mid] == target) {
last = mid;
low = mid + 1;
}
/* If middle element is smaller,
we eliminate the left half */
else if(nums[mid] < target) {
low = mid + 1;
}
/* If middle element is greater,
we eliminate the right half */
else {
high = mid - 1;
}
}
return last;
}
public:
// Function to find the first and last occurrences of the target
vector<int> searchRange(vector<int> &nums, int target) {
// Function call to find the first occurence of target
int first = firstOccurrence(nums, target);
// If the target is not present in the array
if(first == -1) return {-1, -1};
// Function call to find the last occurence of target
int last = lastOccurrence(nums, target);
return {first, last};
}
};
int main()
{
vector<int> nums = {5, 7, 7, 8, 8, 10};
int target = 8;
// Create an instance of the Solution class
Solution sol;
// Function call to find the first and last occurrences
vector<int> result = sol.searchRange(nums, target);
cout << "The first and last occurrences are at indices: "
<< result[0] << " and " << result[1] << "\n";
return 0;
}1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798
import java.util.*;
class Solution {
// Function to find the first occurrence of the target
private int firstOccurrence(int[] nums, int target) {
int low = 0, high = nums.length - 1;
int first = -1;
// Applying Binary Search Algorithm
while(low <= high) {
int mid = low + (high - low) / 2;
/* If the target element is found, we
update the first variable to mid and
eliminate the right half to look for
more smaller index where target is present */
if(nums[mid] == target) {
first = mid;
high = mid - 1;
}
/* If middle element is smaller,
we eliminate the left half */
else if(nums[mid] < target) {
low = mid + 1;
}
/* If middle element is greater,
we eliminate the right half */
else {
high = mid - 1;
}
}
return first;
}
// Function to find the last occurrence of the target
private int lastOccurrence(int[] nums, int target) {
int low = 0, high = nums.length - 1;
int last = -1;
// Applying Binary Search Algorithm
while(low <= high) {
int mid = low + (high - low) / 2;
/* If the target element is found, we
update the first variable to mid and
eliminate the right half to look for
more greater index where target is present */
if(nums[mid] == target) {
last = mid;
low = mid + 1;
}
/* If middle element is smaller,
we eliminate the left half */
else if(nums[mid] < target) {
low = mid + 1;
}
/* If middle element is greater,
we eliminate the right half */
else {
high = mid - 1;
}
}
return last;
}
// Function to find the first and last occurrences of the target
public int[] searchRange(int[] nums, int target) {
// Function call to find the first occurence of target
int first = firstOccurrence(nums, target);
// If the target is not present in the array
if(first == -1) return new int[]{-1, -1};
// Function call to find the last occurence of target
int last = lastOccurrence(nums, target);
return new int[]{first, last};
}
public static void main(String[] args) {
int[] nums = {5, 7, 7, 8, 8, 10};
int target = 8;
// Create an instance of the Solution class
Solution sol = new Solution();
// Function call to find the first and last occurrences
int[] result = sol.searchRange(nums, target);
System.out.println("The first and last occurrences are at indices: "
+ result[0] + " and " + result[1]);
}
}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485
class Solution:
# Function to find the first occurrence of the target
def firstOccurrence(self, nums, target):
low, high = 0, len(nums) - 1
first = -1
# Applying Binary Search Algorithm
while low <= high:
mid = low + (high - low) // 2
# If the target element is found, we
# update the first variable to mid and
# eliminate the right half to look for
# more smaller index where target is present
if nums[mid] == target:
first = mid
high = mid - 1
# If middle element is smaller,
# we eliminate the left half
elif nums[mid] < target:
low = mid + 1
# If middle element is greater,
# we eliminate the right half
else:
high = mid - 1
return first
# Function to find the last occurrence of the target
def lastOccurrence(self, nums, target):
low, high = 0, len(nums) - 1
last = -1
# Applying Binary Search Algorithm
while low <= high:
mid = low + (high - low) // 2
# If the target element is found, we
# update the first variable to mid and
# eliminate the right half to look for
# more greater index where target is present
if nums[mid] == target:
last = mid
low = mid + 1
# If middle element is smaller,
# we eliminate the left half
elif nums[mid] < target:
low = mid + 1
# If middle element is greater,
# we eliminate the right half
else:
high = mid - 1
return last
# Function to find the first and last occurrences of the target
def searchRange(self, nums, target):
# Function call to find the first occurence of target
first = self.firstOccurrence(nums, target)
# If the target is not present in the array
if first == -1:
return [-1, -1]
# Function call to find the last occurence of target
last = self.lastOccurrence(nums, target)
return [first, last]
if __name__ == "__main__":
nums = [5, 7, 7, 8, 8, 10]
target = 8
# Create an instance of the Solution class
sol = Solution()
# Function call to find the first and last occurrences
result = sol.searchRange(nums, target)
print("The first and last occurrences are at indices:", result[0], "and", result[1])123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293
class Solution {
// Function to find the first occurrence of the target
firstOccurrence(nums, target) {
let low = 0, high = nums.length - 1;
let first = -1;
// Applying Binary Search Algorithm
while(low <= high) {
let mid = low + Math.floor((high - low) / 2);
/* If the target element is found, we
update the first variable to mid and
eliminate the right half to look for
more smaller index where target is present */
if(nums[mid] == target) {
first = mid;
high = mid - 1;
}
/* If middle element is smaller,
we eliminate the left half */
else if(nums[mid] < target) {
low = mid + 1;
}
/* If middle element is greater,
we eliminate the right half */
else {
high = mid - 1;
}
}
return first;
}
// Function to find the last occurrence of the target
lastOccurrence(nums, target) {
let low = 0, high = nums.length - 1;
let last = -1;
// Applying Binary Search Algorithm
while(low <= high) {
let mid = low + Math.floor((high - low) / 2);
/* If the target element is found, we
update the first variable to mid and
eliminate the right half to look for
more greater index where target is present */
if(nums[mid] == target) {
last = mid;
low = mid + 1;
}
/* If middle element is smaller,
we eliminate the left half */
else if(nums[mid] < target) {
low = mid + 1;
}
/* If middle element is greater,
we eliminate the right half */
else {
high = mid - 1;
}
}
return last;
}
// Function to find the first and last occurrences of the target
searchRange(nums, target) {
// Function call to find the first occurence of target
let first = this.firstOccurrence(nums, target);
// If the target is not present in the array
if(first == -1) return [-1, -1];
// Function call to find the last occurence of target
let last = this.lastOccurrence(nums, target);
return [first, last];
}
}
let nums = [5, 7, 7, 8, 8, 10];
let target = 8;
// Create an instance of the Solution class
let sol = new Solution();
// Function call to find the first and last occurrences
let result = sol.searchRange(nums, target);
console.log("The first and last occurrences are at indices:", result[0], "and", result[1]);Complexity Analysis:
Time Complexity: O(log N), where N is the size of the given array. Both the firstOccurrence and lastOccurrence functions perform a binary search, which operates in logarithmic time. Thus, the overall time complexity is O(log N).
Space Complexity: O(1), as we are using a constant amount of extra space regardless of the input size. The space used by the variables low, high, mid, first, and last does not depend on the size of the input array.
Frequently Occurring Doubts
Q: How does the algorithm ensure correctness with duplicates?
A: In a sorted array with duplicates: The first binary search stops only when the leftmost occurrence of the target is found. The second binary search ensures the rightmost occurrence is located by adjusting the search bounds appropriately.
Interview Followup Questions
Q: How would you modify the algorithm to find the count of the target value in the array?
A: The count is simply: count=lastIndex−firstIndex+1 This computation is direct and efficient once the first and last occurrences are identified.
Q: Can this algorithm handle floating-point numbers or custom comparison logic?
A: Yes: For floating-point numbers, ensure proper handling of precision in comparisons. For custom logic (e.g., case-insensitive string comparisons), adapt the binary search condition to fit the requirement.
Notes
Code
✅ Testcase
Input: {'nums': '[5, 7, 7, 8, 8, 10]', 'target': '8'}
Expected:
3 4
3 4
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[5, 7, 7, 8, 8, 10]', 'target': '6'}
Expected:
-1 -1
-1 -1
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[5, 7, 7, 8, 8, 10]', 'target': '5'}
Expected:
0 0
0 0
Actual: -
Time: -
sec
Status: Waiting