12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667
#include <bits/stdc++.h>
using namespace std;
// Class to implement Minimum Stack
class MinStack {
private:
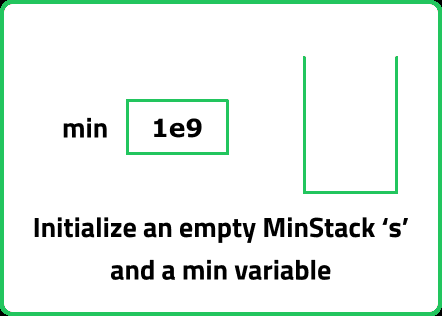
// Initialize a stack
stack <pair<int,int>> st;
public:
// Empty Constructor
MinStack() {
}
// Method to push a value in stack
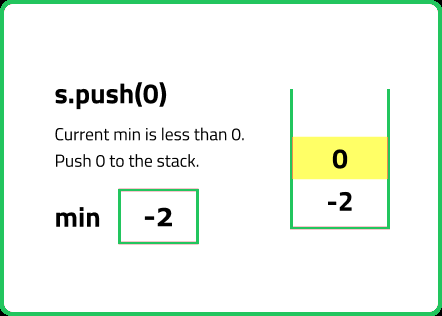
void push(int value) {
// If stack is empty
if(st.empty()) {
// Push current value as minimum
st.push( {value, value} );
return;
}
// Update the current minimum
int mini = min(getMin(), value);
// Add the pair to the stack
st.push({value, mini});
}
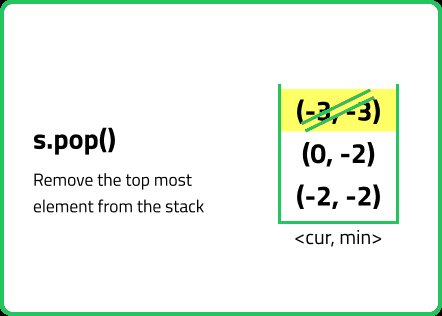
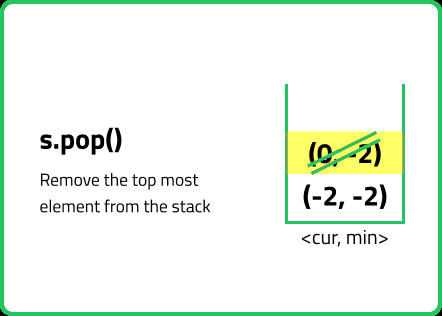
// Method to pop a value from stack
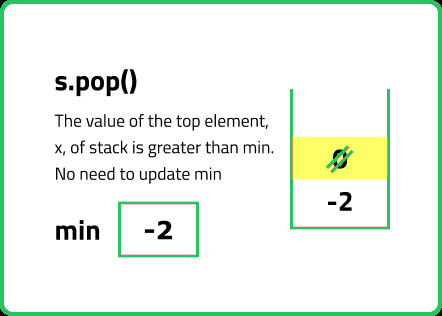
void pop() {
// Using in-built pop method
st.pop();
}
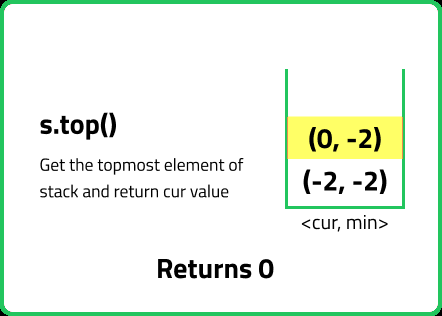
// Method to get the top of stack
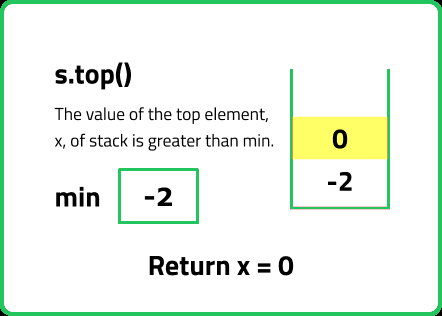
int top() {
// Return the top value
return st.top().first;
}
// Method to get the minimum in stack
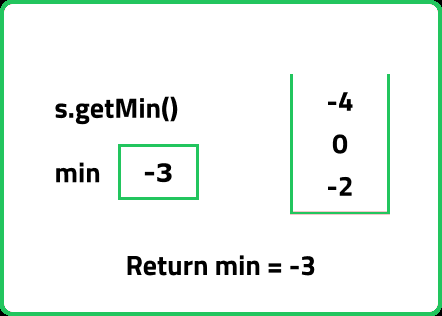
int getMin() {
// Return the minimum
return st.top().second;
}
};
int main() {
MinStack s;
// Function calls
s.push(-2);
s.push(0);
s.push(-3);
cout << s.getMin() << " ";
s.pop();
cout << s.top() << " ";
s.pop();
cout << s.getMin();
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263
import java.util.*;
// Class to implement Minimum Stack
class MinStack {
// Initialize a stack
private Stack<int[]> st;
// Empty Constructor
public MinStack() {
st = new Stack<>();
}
// Method to push a value in stack
public void push(int value) {
// If stack is empty
if (st.isEmpty()) {
// Push current value as minimum
st.push(new int[]{value, value});
return;
}
// Update the current minimum
int mini = Math.min(getMin(), value);
// Add the pair to the stack
st.push(new int[]{value, mini});
}
// Method to pop a value from stack
public void pop() {
// Using in-built pop method
st.pop();
}
// Method to get the top of stack
public int top() {
// Return the top value
return st.peek()[0];
}
// Method to get the minimum in stack
public int getMin() {
// Return the minimum
return st.peek()[1];
}
}
public class Main {
public static void main(String[] args) {
MinStack s = new MinStack();
// Function calls
s.push(-2);
s.push(0);
s.push(-3);
System.out.print(s.getMin() + " ");
s.pop();
System.out.print(s.top() + " ");
s.pop();
System.out.print(s.getMin());
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
class MinStack:
# Empty Constructor
def __init__(self):
# Initialize a stack
self.st = []
# Method to push a value in stack
def push(self, value):
# If stack is empty
if not self.st:
# Push current value as minimum
self.st.append((value, value))
return
# Update the current minimum
mini = min(self.getMin(), value)
# Add the pair to the stack
self.st.append((value, mini))
# Method to pop a value from stack
def pop(self):
# Using in-built pop method
self.st.pop()
# Method to get the top of stack
def top(self):
# Return the top value
return self.st[-1][0]
# Method to get the minimum in stack
def getMin(self):
# Return the minimum
return self.st[-1][1]
if __name__ == "__main__":
s = MinStack()
# Function calls
s.push(-2)
s.push(0)
s.push(-3)
print(s.getMin(), end=" ")
s.pop()
print(s.top(), end=" ")
s.pop()
print(s.getMin())
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
// Class to implement Minimum Stack
class MinStack {
// Initialize a stack
constructor() {
this.st = [];
}
// Method to push a value in stack
push(value) {
// If stack is empty
if (this.st.length === 0) {
// Push current value as minimum
this.st.push([value, value]);
return;
}
// Update the current minimum
const mini = Math.min(this.getMin(), value);
// Add the pair to the stack
this.st.push([value, mini]);
}
// Method to pop a value from stack
pop() {
// Using in-built pop method
this.st.pop();
}
// Method to get the top of stack
top() {
// Return the top value
return this.st[this.st.length - 1][0];
}
// Method to get the minimum in stack
getMin() {
// Return the minimum
return this.st[this.st.length - 1][1];
}
}
// Main function to demonstrate the MinStack functionality
const s = new MinStack();
// Function calls
s.push(-2);
s.push(0);
s.push(-3);
console.log(s.getMin() + " ");
s.pop();
console.log(s.top() + " ");
s.pop();
console.log(s.getMin());