Search X in sorted array
Binary Search
Fundamentals
Easy
- This problem is the basic concept behind search engines
- Whether you're searching for a specific email in your inbox or a keyword on Google, the underlying program is using a more complex version of this algorithm to find and return the results you're looking for
- Without it, the internet as we know it wouldn't exist
Given a sorted array of integers nums with 0-based indexing, find the index of a specified target integer. If the target is found in the array, return its index. If the target is not found, return -1.
Examples:
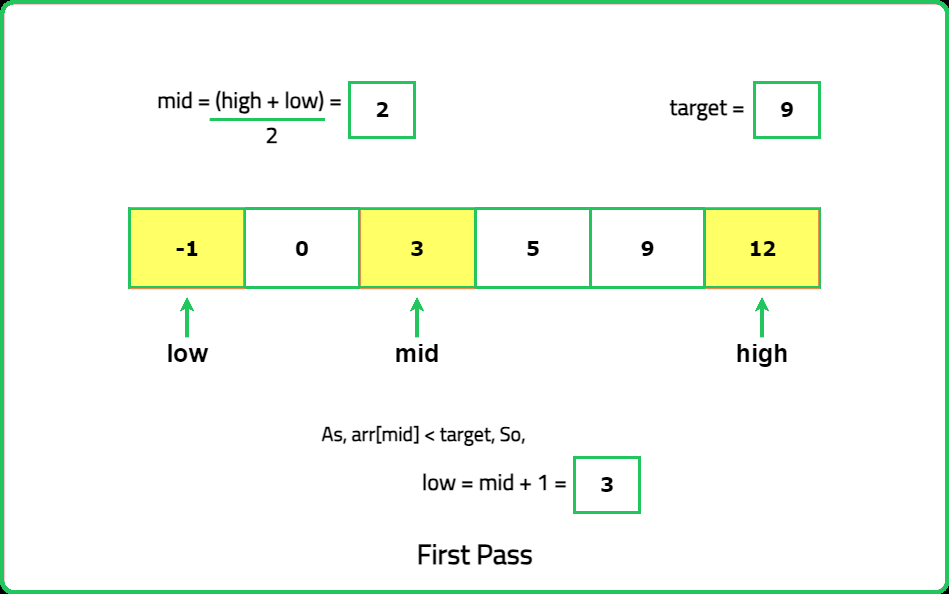
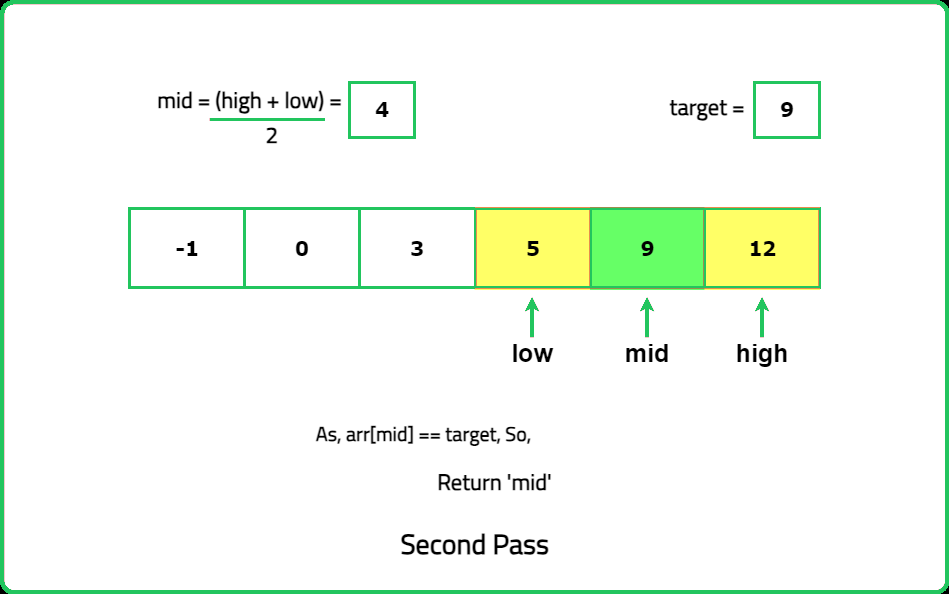
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: The target integer 9 exists in nums and its index is 4
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: The target integer 2 does not exist in nums so return -1
Input: nums = [-1,0,3,5,9,12], target = -1
Constraints
- 1 <= nums.length <= 105
- -105 < nums[i], target < 105
- nums is sorted in ascending order.
Hints
- Instead of scanning through the array element by element (linear search), leverage the fact that the array is sorted. Divide the search space into halves repeatedly to locate the target. Each step either discards or keeps half the array.
- Always start by calculating the midpoint of the current search range. If the midpoint value matches the target, you’re done. If it’s smaller, the target must be on the right; if larger, it must be on the left.
Company Tags
Mastercard
Epic Systems
Walmart
PwC
Morgan Stanley
Rockstar Games
Western Digital
JPMorgan Chase
Byju's
Ernst & Young
OYO Rooms
Splunk
DoorDash
GE Healthcare
Stripe
Wayfair
Lyft
Dropbox
NVIDIA
Shopify
Red Hat
Ubisoft
McKinsey & Company
KPMG
Teladoc Health
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro