Check if the number is armstrong

Beginner Problems Basic Maths Easy

Fun Fact: While the Armstrong number itself might not have a direct application in software development, the underlying logic of dealing with integer manipulation, loops, and conditionals can be found in various aspects of coding like data validation, checksum algorithms or hash functions
Algorithms to identify Armstrong numbers act as brain teasers to improve logical thinking and problem-solving skills which are essential in breaking down complex software development tasks
For instance, the concept can be used in encryption algorithms to add an extra layer of security

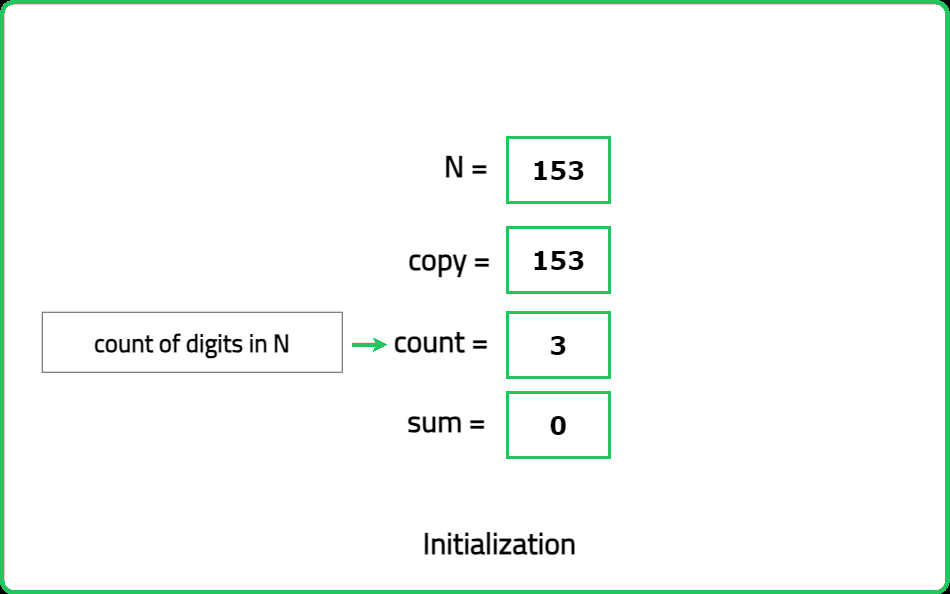
You are given an integer n. You need to check whether it is an armstrong number or not. Return true if it is an armstrong number, otherwise return false.

An armstrong number is a number which is equal to the sum of the digits of the number, raised to the power of the number of digits.

Examples:

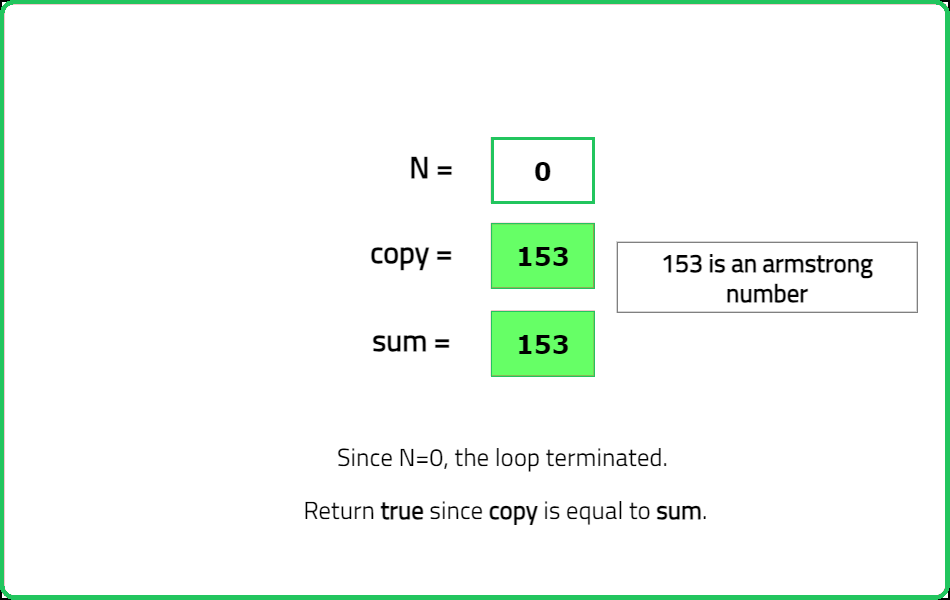
Input: n = 153

Output: true

Explanation: Number of digits : 3.

1 ^ 3 + 5 ^ 3 + 3 ^ 3 = 1 + 125 + 27 = 153.

Therefore, it is an Armstrong number.

Input: n = 12

Output: false

Explanation: Number of digits : 2.

1 ^ 2 + 2 ^ 2 = 1 + 4 = 5.

Therefore, it is not an Armstrong number.

Input: n = 370

Constraints

0 <= n <= 5000

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

Intuition:

Given a number, the number of digits can be found. Once the number of digits is known, all the digits can be extracted one by one from the right which can be used to check whether the number is Armstrong or not.

Approach:

Initialize three variables:
- count - to store the count of digits in the given number.
- sum - to store the sum of the digits of the number raised to the power of the number of digits.
- copy - to store the copy of the original number.
Start iterating on the given number till there are digits left to extract. In each iteration, extract the last digit (using the modulus operator with 10), and add the digit raised to the power of count to sum. Update n by integer division with 10 effectively removing the last digit.
After the iterations are over, check if the copy of the original is the same as the sum stored. If found equal, the original number is an Armstrong number, else it is not.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to count the 
    number of digits in N */
    int countDigit(int n) {
        int count = log10(n) + 1;
        return count;
    }
    
public:
    /* Function to find whether the
    number is Armstrong or not */
    bool isArmstrong(int n) {
        
        // Store the count of digits
        int count = countDigit(n);
        
        // Variable to store the sum
        int sum = 0;
        
        // Variable to store the copy
        int copy = n;
        
        /* Iterate through each
        digit of the number */
        while(n > 0){
            
            // Extract the last digit
            int lastDigit = n % 10;
            
            // Update sum
            sum += pow(lastDigit, count); 
            
            /* Remove the last digit
             from the number */
            n = n / 10;
        }
        
        /* Check if the sum of digits raised to the
        power of k equals the original number */
        if(sum == copy) return true;
        return false;
    }
};

int main() {
    int n = 153;
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find whether the
     given number is Armstrong or not */
    bool ans = sol.isArmstrong(n);
    
    if(ans) {
        cout << n << " is an Armstrong number." << endl;
    } else {
        cout << n << " is not an Armstrong number." << endl;
    }
    
    return 0;
}
import java.util.*;

class Solution {
    /* Function to count the 
    number of digits in N */
    private int countDigit(int n) {
        int count = (int)(Math.log10(n) + 1);
        return count;
    }

    /* Function to find whether the
    number is Armstrong or not */
    public boolean isArmstrong(int n) {
        
        // Store the count of digits
        int count = countDigit(n);
        
        // Variable to store the sum
        int sum = 0;
        
        // Variable to store the copy
        int copy = n;
        
        /* Iterate through each
        digit of the number */
        while (n > 0) {
            
            // Extract the last digit
            int lastDigit = n % 10;
            
            // Update sum
            sum += Math.pow(lastDigit, count);
            
            /* Remove the last digit
             from the number */
            n = n / 10;
        }
        
        /* Check if the sum of digits raised to the
        power of k equals the original number */
        if (sum == copy) return true;
        return false;
    }

    public static void main(String[] args) {
        int n = 153;
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution();
        
        /* Function call to find whether the
        given number is Armstrong or not */
        boolean ans = sol.isArmstrong(n);
        
        if (ans) {
            System.out.println(n + " is an Armstrong number.");
        } else {
            System.out.println(n + " is not an Armstrong number.");
        }
    }
}
import math

class Solution:

    """ Function to count the 
    number of digits in N """
    def countDigit(self, n):
        
        # Base case
        if n == 0:
            return 1

        count = int(math.log10(n)) + 1
        return count
    
    """ Function to find whether the
    number is Armstrong or not """
    def isArmstrong(self, n):
        # Store the count of digits
        count = self.countDigit(n)
        
        # Variable to store the sum
        sum = 0
        
        # Variable to store the copy
        copy = n
        
        # Iterate through each
        # digit of the number
        while n > 0:
            
            # Extract the last digit
            lastDigit = n % 10
            
            # Update sum
            sum += pow(lastDigit, count)
            
            # Remove the last digit
            # from the number
            n = n // 10
        
        # Check if the sum of digits raised to the
        # power of k equals the original number
        if sum == copy:
            return True
        return False
        
# Main function
if __name__ == "__main__":
    n = 153
    
    # Creating an instance of 
    # Solution class
    sol = Solution()
    
    # Function call to find whether the
    # given number is Armstrong or not
    ans = sol.isArmstrong(n)
    
    if ans:
        print(f"{n} is an Armstrong number.")
    else:
        print(f"{n} is not an Armstrong number.")
class Solution {
    /* Function to count the 
    number of digits in N */
    countDigit(n) {
        let count = Math.floor(Math.log10(n)) + 1;
        return count;
    }

    /* Function to find whether the
    number is Armstrong or not */
    isArmstrong(n) {
        
        // Store the count of digits
        let count = this.countDigit(n);
        
        // Variable to store the sum
        let sum = 0;
        
        // Variable to store the copy
        let copy = n;
        
        /* Iterate through each
        digit of the number */
        while (n > 0) {
            
            // Extract the last digit
            let lastDigit = n % 10;
            
            // Update sum
            sum += Math.pow(lastDigit, count);
            
            /* Remove the last digit
             from the number */
            n = Math.floor(n / 10);
        }
        
        /* Check if the sum of digits raised to the
        power of k equals the original number */
        if (sum == copy) return true;
        return false;
    }
}

// Main function
let n = 153;

// Creating an instance of 
// Solution class
let sol = new Solution();

/* Function call to find whether the
 given number is Armstrong or not */
let ans = sol.isArmstrong(n);

if (ans) {
    console.log(`${n} is an Armstrong number.`);
} else {
    console.log(`${n} is not an Armstrong number.`);
}

Complexity Analysis:

Time Complexity: O(log₁₀(N)) – N is being divided by 10 until it becomes zero resulting in log₁₀(N) iterations and in each iteration constant time operations are performed.

Space Complexity: O(1) – Using a couple of variables i.e., constant space, regardless of the size of the input.

Code

Problem List