Combination Sum III
Recursion
FAQs (Medium)
Medium
- Fun Fact: This problem is a variant of the classic combinatorial problem in computer science often encountered in financial software, where an organization might want to understand all possible combinations of assets that can achieve a given financial target
- Beyond finance, it also broadly applies in decision-making algorithms, such as in Artificial Intelligence for exploring all potential paths or actions
- By enumerating all possibilities, the software can make more informed decisions to achieve the desired goal
Determine all possible set of k numbers that can be added together to equal n while meeting the following requirements:
- There is only use of numerals 1 through 9.
- A single use is made of each number.
Return list of every feasible combination that is allowed. The combinations can be returned in any order, but the list cannot have the same combination twice.
Examples:
Input : k = 3 , n = 7
Output : [ [1, 2, 4] ]
Explanation :
1 + 2 + 4 = 7
There are no other valid combinations.
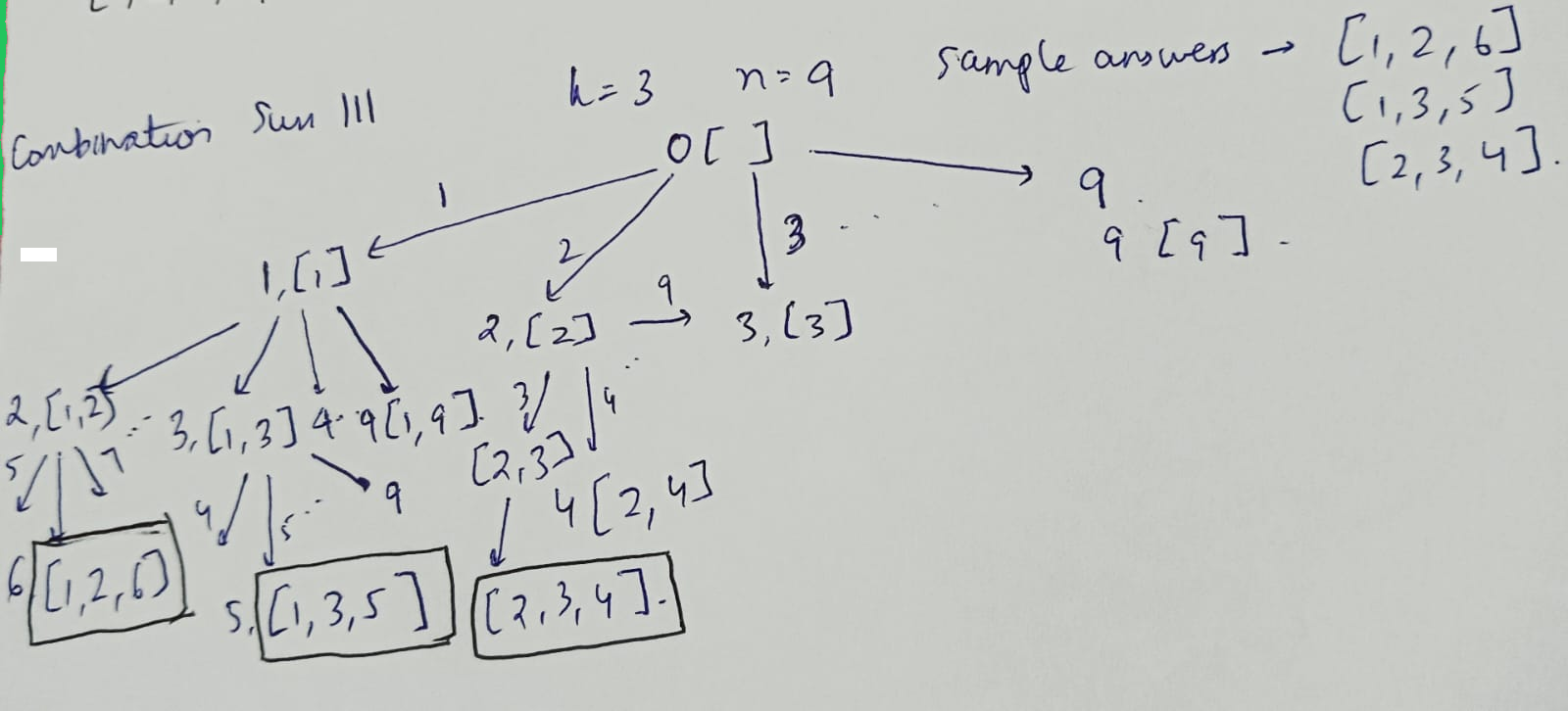
Input : k = 3, n = 9
Output : [[1, 2, 6],[1, 3, 5],[2, 3, 4]]
Explanation :
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.
Input : k = 3, n = 8
Constraints
- 2 <= k <= 9
- 1 <= n <= 60
Hints
- "Use recursion to explore combinations. Include a number from 1 to 9 and reduce both n (target sum) and k (remaining numbers to select). Exclude the current number and move to the next."
- Generate combinations by iterating through numbers from the current index to ensure each number is used only once. This avoids generating duplicate combinations.
Company Tags
GE Healthcare
Lyft
Medtronic
Nutanix
Byju's
Morgan Stanley
Johnson & Johnson
IBM
Mastercard
DoorDash
Texas Instruments
ARM
NVIDIA
Freshworks
Airbnb
Alibaba
MongoDB
Riot Games
Electronic Arts
eBay
Zynga
Unity Technologies
HashiCorp
Cerner
Zomato
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
 ---!>
---!>