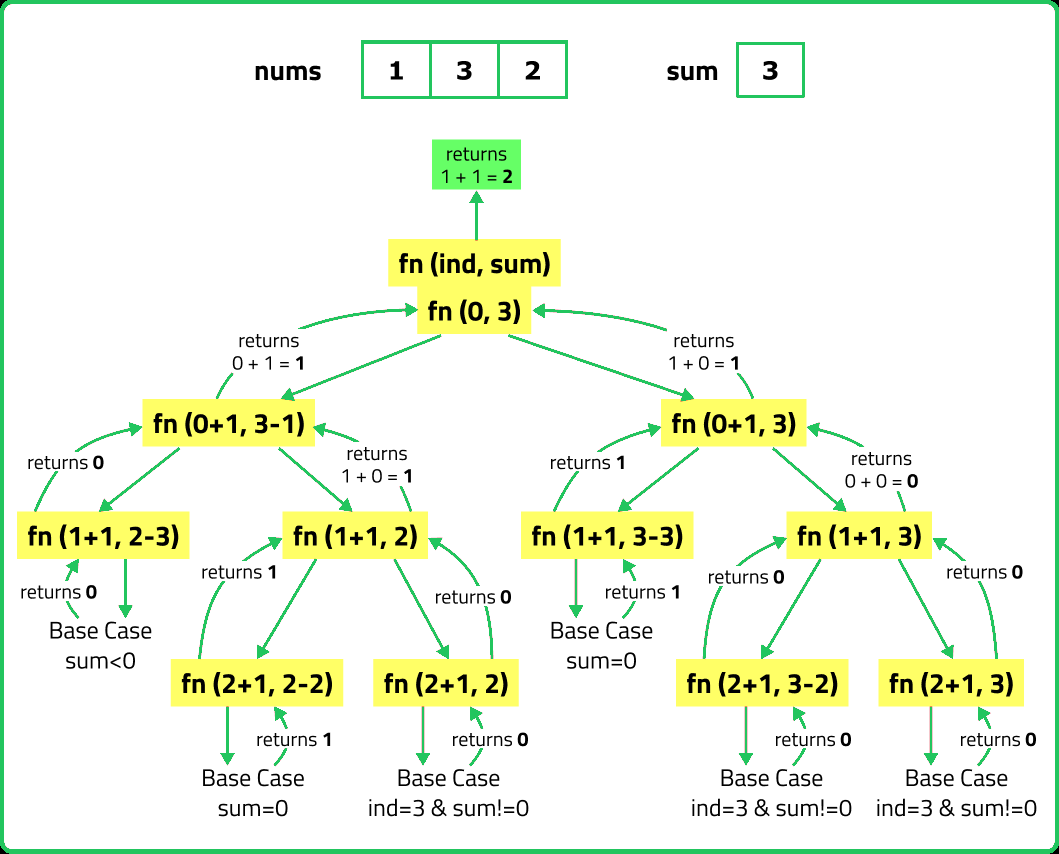
Count all subsequences with sum K
Recursion
Subsequence Pattern Problems
Easy
- Fun Fact: The "sum of subsequence equals K" problem concept has a broad range of applications
- It is primarily used in financial software for portfolio optimization and risk management
- For example, an investor may want to find all combinations of stocks (subsequences from an array of available stocks) that result in a specific target return (sum equals to K)
- Optimizing and streamlining this process can result in substantial investment efficiency
- It is also used in budgeting apps for determining possible allocations of available resources to achieve a financial goal
Given an array nums and an integer k.Return the number of non-empty subsequences of nums such that the sum of all elements in the subsequence is equal to k.
Examples:
Input : nums = [4, 9, 2, 5, 1] , k = 10
Output : 2
Explanation : The possible subsets with sum k are [9, 1] , [4, 5, 1].
Input : nums = [4, 2, 10, 5, 1, 3] , k = 5
Output : 3
Explanation : The possible subsets with sum k are [4, 1] , [2, 3] , [5].
Input : nums = [1, 10, 4, 5] , k = 16
Constraints
- 1 <= nums.length <= 20
- 1 <= nums[i] <= 100
- 1 <= k <= 2000
Hints
- Use a boolean DP array dp where dp[j] represents whether a subset with sum j can be formed.
- "Recursively explore all combinations of elements: Either include the current element in the subset or skip it. If the sum equals k at any point, return True."
Company Tags
Teladoc Health
Roblox
Airbnb
Rockstar Games
MongoDB
OYO Rooms
Oracle
Boston Consulting Group
DoorDash
Optum
Rakuten
Snowflake
Databricks
Bain & Company
Shopify
Square
Byju's
Chewy
Cloudflare
Riot Games
Bungie
AMD
Lyft
Stripe
PayPal
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro