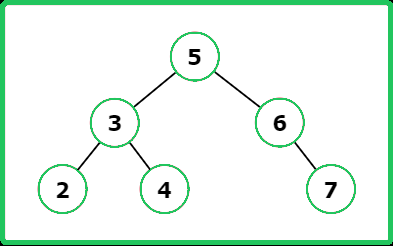
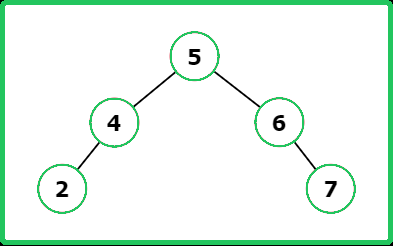
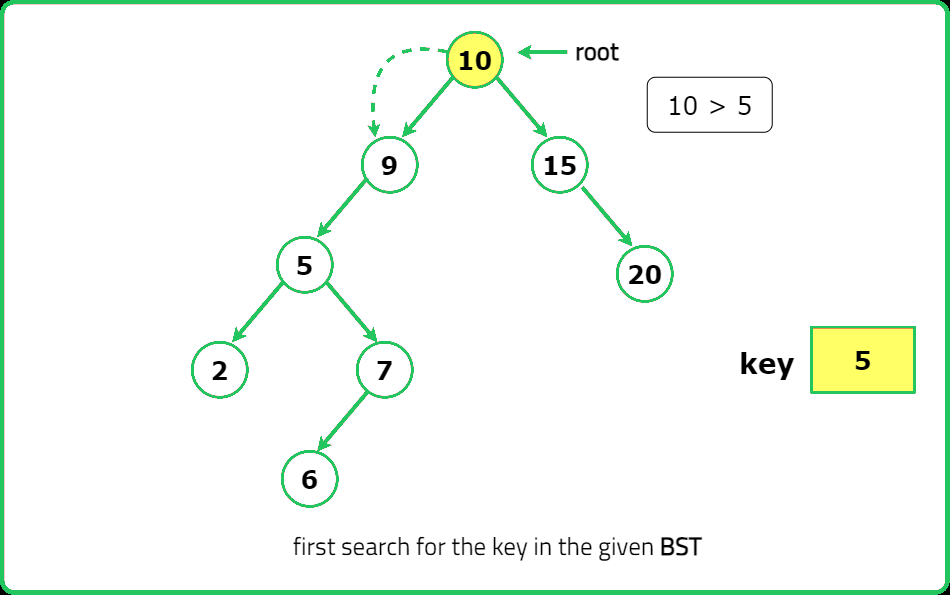
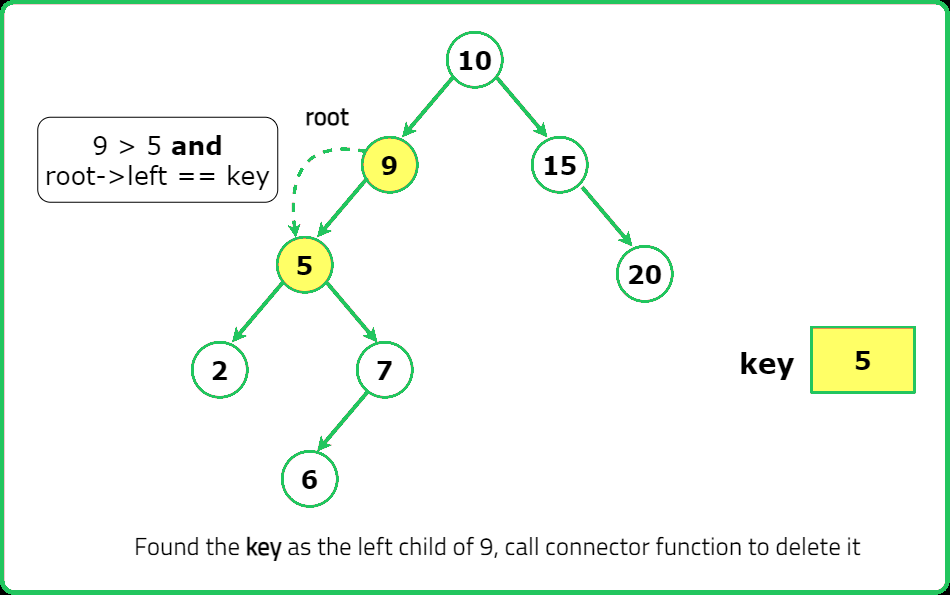
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107
#include <bits/stdc++.h>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : data(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Helper function to connect subtrees after deleting a node
TreeNode* connector(TreeNode* root) {
// Case 1: If the node has no left child,
// return the right subtree to bypass the node.
if (!root->left)
return root->right;
// Case 2: If the node has no right child,
// return the left subtree to bypass the node.
else if (!root->right)
return root->left;
/*
Case 3: If the node has both left and right children:
1. Save the left subtree in a temporary variable.
2. Find the leftmost node in the right subtree.
3. Attach the left subtree to the leftmost node in the right subtree. */
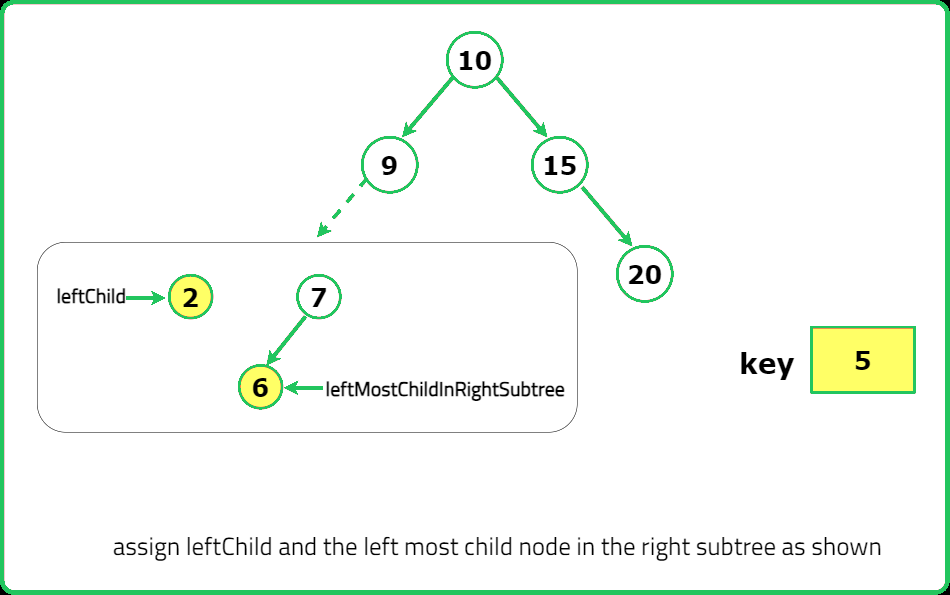
TreeNode* leftchild = root->left;
TreeNode* leftmost_child_in_right_subtree = root->right;
// Traverse to the leftmost node in the right subtree.
while (leftmost_child_in_right_subtree->left) {
leftmost_child_in_right_subtree =
leftmost_child_in_right_subtree->left;
}
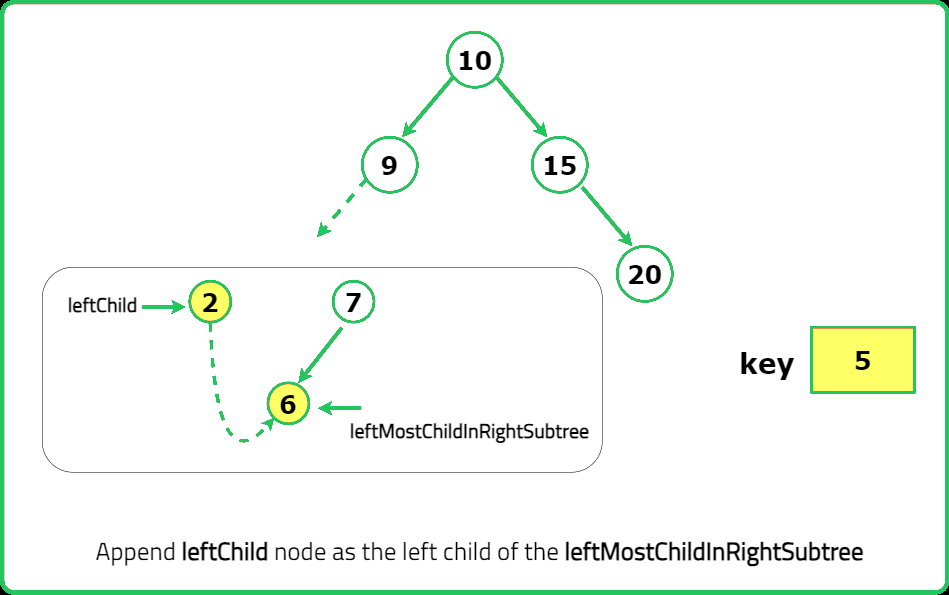
// Attach the left subtree to the leftmost node in the right subtree.
leftmost_child_in_right_subtree->left = leftchild;
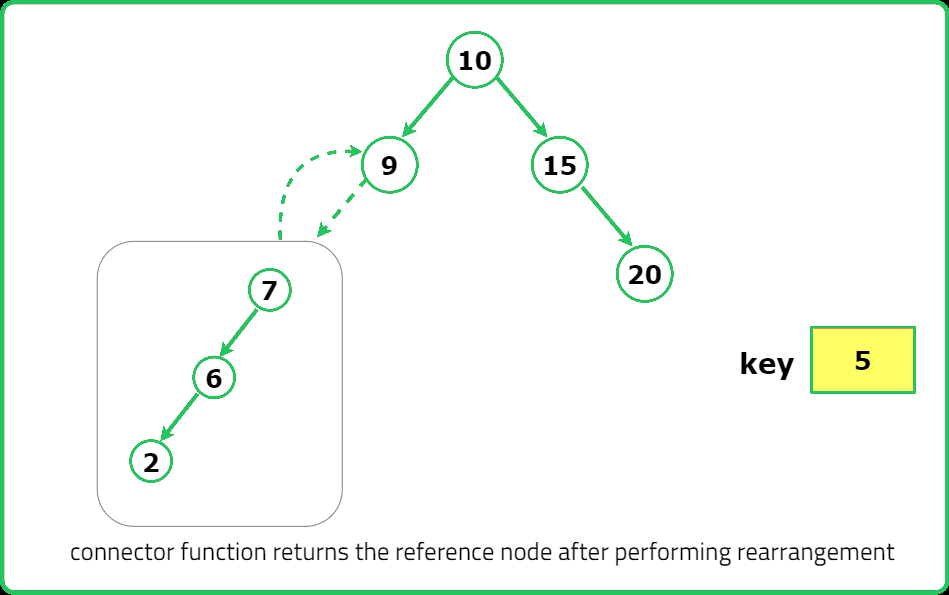
// Return the right subtree as the new root of the modified tree.
return root->right;
}
// Function to delete a node with a specific key from the binary search tree
TreeNode* deleteNode(TreeNode* root, int key) {
// Base case: if the tree is empty, return NULL.
if (root == NULL)
return NULL;
// If the node to be deleted is the root node,
// use the connector function to replace the root.
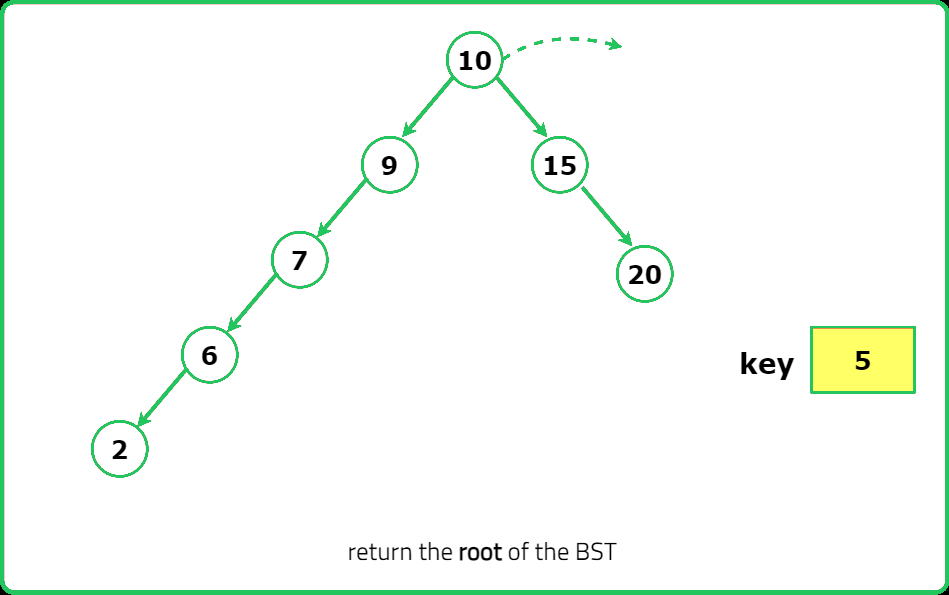
if (root->data == key) {
return connector(root);
}
// Traverse the tree to find the node to be deleted.
TreeNode* node = root;
while (node) {
// If the key to be deleted is smaller than the current node's data,
// move to the left subtree.
if (node->data > key) {
// If the left child is the node to be deleted,
// update the left child with the connector function.
if (node->left && node->left->data == key) {
node->left = connector(node->left);
break;
} else {
node = node->left;
}
}
// If the key to be deleted is larger than the current node's data,
// move to the right subtree.
else {
// If the right child is the node to be deleted,
// update the right child with the connector function.
if (node->right && node->right->data == key) {
node->right = connector(node->right);
break;
} else {
node = node->right;
}
}
}
// Return the modified tree with the node deleted.
return root;
}
};
int main() {
// Create a sample binary search tree.
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(3);
root->right = new TreeNode(8);
root->left->left = new TreeNode(2);
root->left->right = new TreeNode(4);
Solution sol;
// Delete node with key 3 from the tree.
root = sol.deleteNode(root, 3);
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697
// Definition for a binary tree node.
public class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) { data = val; left = null, right = null }
}
class Solution {
// Helper function to connect subtrees after deleting a node
private TreeNode connector(TreeNode root) {
// Case 1: If the node has no left child,
// return the right subtree to bypass the node.
if (root.left == null) return root.right;
// Case 2: If the node has no right child,
// return the left subtree to bypass the node.
if (root.right == null) return root.left;
/*
Case 3: If the node has both left and right children:
1. Save the left subtree in a temporary variable.
2. Find the leftmost node in the right subtree.
3. Attach the left subtree to the leftmost node in the right subtree. */
TreeNode leftChild = root.left;
TreeNode leftmostChildInRightSubtree = root.right;
// Traverse to the leftmost node in the right subtree.
while (leftmostChildInRightSubtree.left != null) {
leftmostChildInRightSubtree = leftmostChildInRightSubtree.left;
}
// Attach the left subtree to the leftmost node in the right subtree.
leftmostChildInRightSubtree.left = leftChild;
// Return the right subtree as the new root of the modified tree.
return root.right;
}
// Function to delete a node with a specific key from the binary search tree
public TreeNode deleteNode(TreeNode root, int key) {
// Base case: if the tree is empty, return null.
if (root == null) return null;
// If the node to be deleted is the root node,
// use the connector function to replace the root.
if (root.data == key) {
return connector(root);
}
// Traverse the tree to find the node to be deleted.
TreeNode node = root;
while (node != null) {
// If the key to be deleted is smaller than the current node's data,
// move to the left subtree.
if (node.data > key) {
// If the left child is the node to be deleted,
// update the left child with the connector function.
if (node.left != null && node.left.data == key) {
node.left = connector(node.left);
break;
} else {
node = node.left;
}
}
// If the key to be deleted is larger than the current node's data,
// move to the right subtree.
else {
// If the right child is the node to be deleted,
// update the right child with the connector function.
if (node.right != null && node.right.data == key) {
node.right = connector(node.right);
break;
} else {
node = node.right;
}
}
}
// Return the modified tree with the node deleted.
return root;
}
public static void main(String[] args) {
// Create a sample binary search tree.
TreeNode root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(8);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
Solution sol = new Solution();
// Delete node with key 3 from the tree.
root = sol.deleteNode(root, 3);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687
class TreeNode:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
class Solution:
# Helper function to connect subtrees after deleting a node
def connector(self, root):
# If the node has no left child, return the right subtree.
# This effectively removes the node by bypassing it with its right child.
if not root.left:
return root.right
# If the node has no right child, return the left subtree.
# This effectively removes the node by bypassing it with its left child.
elif not root.right:
return root.left
# If the node has both left and right children, handle the case as follows:
# 1. Save the left subtree in a temporary variable.
# 2. Find the leftmost node in the right subtree.
# 3. Attach the left subtree to the leftmost node in the right subtree.
leftchild = root.left
leftmost_child_in_right_subtree = root.right
# Traverse to the leftmost node in the right subtree.
while leftmost_child_in_right_subtree.left:
leftmost_child_in_right_subtree = leftmost_child_in_right_subtree.left
# Attach the left subtree to the leftmost node in the right subtree.
leftmost_child_in_right_subtree.left = leftchild
# Return the right subtree as the new root of the modified tree.
return root.right
# Function to delete a node with a specific key from the binary search tree.
def deleteNode(self, root, key):
# If the tree is empty, there is nothing to delete.
if root is None:
return None
# If the node to be deleted is the root node, use the connector function.
if root.data == key:
return self.connector(root)
# Traverse the tree to find the node to be deleted.
node = root
while node:
# If the key to be deleted is smaller than the current node's data,
# move to the left subtree.
if node.data > key:
# If the left child is the node to be deleted, update the left child.
if node.left and node.left.data == key:
node.left = self.connector(node.left)
break
else:
node = node.left
# If the key to be deleted is larger than the current node's data,
# move to the right subtree.
else:
# If the right child is the node to be deleted, update the right child.
if node.right and node.right.data == key:
node.right = self.connector(node.right)
break
else:
node = node.right
# Return the modified tree with the node deleted.
return root
# Example usage
if __name__ == "__main__":
# Create a sample binary search tree
root = TreeNode(5)
root.left = TreeNode(3)
root.right = TreeNode(8)
root.left.left = TreeNode(2)
root.left.right = TreeNode(4)
sol = Solution()
# Delete node with key 3 from the tree
root = sol.deleteNode(root, 3)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102
class TreeNode {
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
}
}
class Solution {
// Helper function to connect subtrees after deleting a node
connector(root) {
// Case 1: If the node has no left child,
// return the right subtree to bypass the node.
if (!root.left) return root.right;
// Case 2: If the node has no right child,
// return the left subtree to bypass the node.
else if (!root.right) return root.left;
/*
Case 3: If the node has both left and right children:
1. Save the left subtree in a temporary variable.
2. Find the leftmost node in the right subtree.
3. Attach the left subtree to the leftmost node in the right subtree.
*/
let leftChild = root.left;
let leftmostChildInRightSubtree = root.right;
// Traverse to the leftmost node in the right subtree.
while (leftmostChildInRightSubtree.left) {
leftmostChildInRightSubtree = leftmostChildInRightSubtree.left;
}
// Attach the left subtree to the leftmost node in the right subtree.
leftmostChildInRightSubtree.left = leftChild;
// Return the right subtree as the new root of the modified tree.
return root.right;
}
// Function to delete a node with a specific key from the binary search tree
deleteNode(root, key) {
// Base case: if the tree is empty, return null.
if (root === null) return null;
// If the node to be deleted is the root node,
// use the connector function to replace the root.
if (root.data === key) {
return this.connector(root);
}
// Traverse the tree to find the node to be deleted.
let node = root;
while (node) {
// If the key to be deleted is smaller than the current node's data,
// move to the left subtree.
if (node.data > key) {
// If the left child is the node to be deleted,
// update the left child with the connector function.
if (node.left && node.left.data === key) {
node.left = this.connector(node.left);
break;
} else {
node = node.left;
}
}
// If the key to be deleted is larger than the current node's data,
// move to the right subtree.
else {
// If the right child is the node to be deleted,
// update the right child with the connector function.
if (node.right && node.right.data === key) {
node.right = this.connector(node.right);
break;
} else {
node = node.right;
}
}
}
// Return the modified tree with the node deleted.
return root;
}
}
// Example usage
function main() {
// Create a sample binary search tree.
let root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(8);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
let sol = new Solution();
// Delete node with key 3 from the tree.
root = sol.deleteNode(root, 3);
}
main();