Maximum sum of non adjacent elements

Dynamic Programming 1D DP Medium Go Ad-Free - ₹20/mo

Given an integer array nums of size n. Return the maximum sum possible using the elements of nums such that no two elements taken are adjacent in nums.

A subsequence of array is a sequence that can be derived from the array by deleting some or no elements without changing the order of the remaining elements.

Examples:

Input: nums = [1, 2, 4]

Output: 5

Explanation: [1, 2, 4], the underlined elements are taken to get the maximum sum.

Input: nums = [2, 1, 4, 9]

Output: 11

Explanation: [2, 1, 4, 9], the underlined elements are taken to get the maximum sum.

Input: nums = [1, 7, 16, 8]

Constraints

n == nums.length
1 <= n <= 10⁵
0 <= nums[i] <= 1000

Hints

"Consider the two choices at each step i: Take nums[i] → Add nums[i] to the sum and skip the next element (i+1). Skip nums[i] → Move to the next element (i+1) without adding anything."
"Using dynamic programming (O(n)), we store the dp[] values to avoid redundant calculations. Further optimization reduces space complexity from O(n) to O(1), using two variables to track dp[i-1] and dp[i-2]."

Company Tags

Seagate Technology Zomato Salesforce eBay Zoho Flipkart NVIDIA Red Hat Activision Blizzard Oracle HCL Technologies Qualcomm MongoDB Alibaba McKinsey & Company Visa Mastercard Byju's Rockstar Games Ubisoft Chewy Cerner Snowflake ARM Bungie Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

As discussed in the previous problems that rercursion can be used when the problem is asking for minimum/maximum of something. Here in this problem it is asking for maximum sum of subsequences, one approach that comes to our mind is to generate all subsequences and pick the one with the maximum sum.

To generate all the subsequences, we can use the pick/non-pick technique. This technique can be briefly explained as follows:

At every index of the array, we have two options:

First, to pick the array element at that index and consider it in our subsequence.

Second, to leave the array element at that index and not to consider it in our subsequence.

Now, we will try to form the recursive solution to the problem with the pick/non-pick technique. There is one more catch, the problem wants us to have only non-adjacent elements of the array in the subsequence, therefore we need to address that too. In order to do that, while moving ahead, we can keep a track if we took the last index or not.

Steps to form recursive solution:

Represent the function in terms of indices: We are given an array which can be easily thought of in terms of indices, at each index an element will be present. f(n-1) will return the maximum sum from 0th index till (n-1)th index. We need to return f(n-1) as our final answer.

Try all the choices to reach the goal: As mentioned earlier we will use the pick/non-pick technique to generate all subsequences. In addition to that only pick up the non-adjacent elements in this step.

There are two possible choices that can be made for each index. If we pick an element then, pick = arr[ind] + f(ind-2). The reason we are doing f(ind-2) is because we have picked the current index(ind) element so we need to pick a non-adjacent element so we choose the index ‘ind-2’ instead of ‘ind-1’.

The other chice can be to ignore the current element at index(ind) in our subsequence. So nonPick= 0 + f(ind-1). As we don’t pick the current element, we can consider the adjacent element in the subsequence.

/*It is pseudocode and it is not tied to 
any specific programming language*/
f(ind, arr[]){
    //base condition
    pick = arr[ind] + find(ind-2, arr)
    notPick = 0 + f(ind-1, arr)
}

Take the maximum of all the choices: As the problem statement asks to find the maximum sum, return the maximum of two choices made in the above step.

/*It is pseudocode and it is not tied to
 any specific programming language*/
f(ind, arr[]){
    //base condition
    pick = arr[ind] + f(ind-2, arr)
    notPick = 0 + f(ind - 1, arr)
    return max(pick, notPick)
}

Base Conditions: If ind=0, then we know to reach at index=0, we would have ignored the element at index = 1. Therefore, we can simply return the value of arr[ind] and consider it in the subsequence. If ind<0, this case can hit when we call f(ind-2) at ind=1. In this case we want to return to the calling function so we simply return 0 so that nothing is added to the subsequence sum.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to solve the problem using recursion
    int func(int ind, vector<int>& arr) {
    // Base cases
    if (ind == 0) 
        return arr[ind];
    if (ind < 0)  
        return 0;

    // Choosing the current element
    int pick = arr[ind] + func(ind - 2, arr);  
    
    // Skipping the current element
    int nonPick = 0 + func(ind - 1, arr);  

    // Return the maximum 
    return max(pick, nonPick);
}
public:
    /*Function to calculate the maximum
    sum of nonAdjacent elements d*/
    int nonAdjacent(vector<int>& nums) {
        int ind = nums.size()-1;
        
        //Return the maximum sum
        return func(ind, nums);
    }
};

int main() {
    vector<int> arr{2, 1, 4, 9};
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the solve function and print the result
    cout << sol.nonAdjacent(arr);

    return 0;
}
import java.util.*;

class Solution {
    // Function to solve the problem using recursion
    private int func(int ind, int[] arr) {
        // Base cases
        if (ind == 0)
            return arr[ind];
        if (ind < 0)
            return 0;

        // Choosing the current element
        int pick = arr[ind] + func(ind - 2, arr);

        // Skipping the current element
        int nonPick = 0 + func(ind - 1, arr);

        // Return the maximum
        return Math.max(pick, nonPick);
    }

    /* Function to calculate the maximum
    sum of non-adjacent elements*/
    public int nonAdjacent(int[] nums) {
        int ind = nums.length - 1;

        // Return the maximum sum
        return func(ind, nums);
    }

    public static void main(String[] args) {
        int[] arr = {2, 1, 4, 9};

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the nonAdjacent function and print the result
        System.out.println(sol.nonAdjacent(arr));
    }
}
class Solution:
    
    # Function to solve the problem using recursion
    def func(self, ind, arr):
        # Base cases
        if ind == 0:
            return arr[ind]
        if ind < 0:
            return 0

        # Choosing the current element
        pick = arr[ind] + self.func(ind - 2, arr)

        # Skipping the current element
        nonPick = 0 + self.func(ind - 1, arr)

        # Return the maximum
        return max(pick, nonPick)

    """ Function to calculate the maximum
    sum of non-adjacent elements"""
    def nonAdjacent(self, nums):
        ind = len(nums) - 1

        # Return the maximum sum
        return self.func(ind, nums)

if __name__ == "__main__":
    arr = [2, 1, 4, 9]

    # Create an instance of Solution class
    sol = Solution()

    # Call the nonAdjacent function and print the result
    print(sol.nonAdjacent(arr))
class Solution {
    
    // Function to solve the problem using recursion
    func(ind, arr) {
        // Base cases
        if (ind === 0) {
            return arr[ind];
        }
        if (ind < 0) {
            return 0;
        }

        // Choosing the current element
        let pick = arr[ind] + this.func(ind - 2, arr);

        // Skipping the current element
        let nonPick = 0 + this.func(ind - 1, arr);

        // Return the maximum
        return Math.max(pick, nonPick);
    }

    /* Function to calculate the maximum
    sum of non-adjacent elements */
    nonAdjacent(nums) {
        let ind = nums.length - 1;

        // Return the maximum sum
        return this.func(ind, nums);
    }
}
    let arr = [2, 1, 4, 9];

    // Create an instance of Solution class
    let sol = new Solution();

    // Call the nonAdjacent function and print the result
    console.log(sol.nonAdjacent(arr));

Complexity Analysis:

Time Complexity: O(2^N), where N is the given size of array. This is because each call branches into two more calls, leading to an exponential growth in the number of calls.

Space Complexity:The space complexity of this recursive approach is O(n). This is because the maximum depth of the recursion stack can go up to n, due to the linear nature of the stack usage relative to the input size n.

If we observe the recursion tree, we will observe a number of overlapping subproblems. Therefore the recursive solution can be memoized to reduce the time complexity.

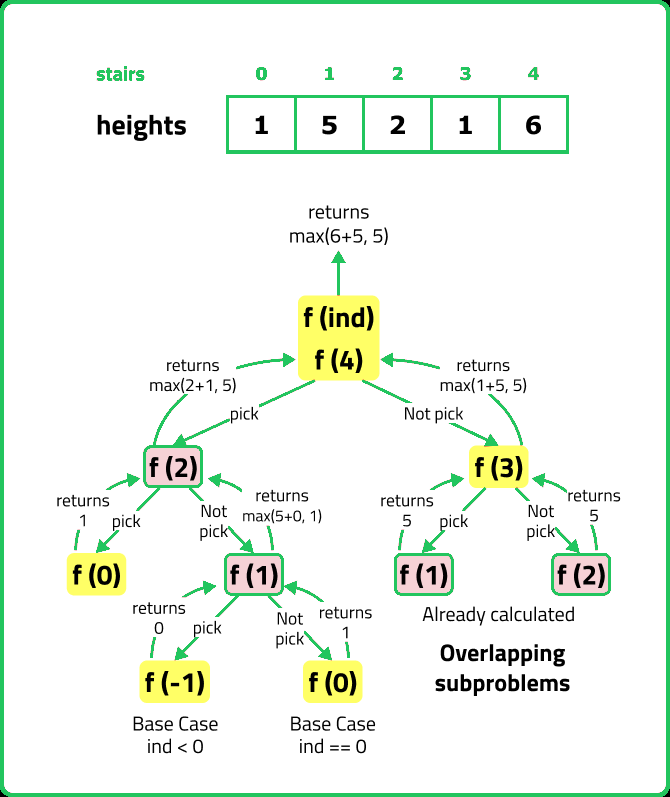
Steps to convert Recursive code to memoization solution:

Declare an Array dp[] of Size n: Here, n is the size of the given array in the problem, as the highest number of subproblems can be n(including 0 as well). It represents the solution to the subproblem for any given index. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to solve the problem using memoization
    int func(int ind, vector<int> &arr, vector<int> &dp) {
    // Base cases
    if (ind == 0) 
        return arr[ind];
    if (ind < 0)  
        return 0;
    
    if(dp[ind] != -1){
        return dp[ind];
    }
    // Choosing the current element
    int pick = arr[ind] + func(ind - 2, arr, dp);  
    
    // Skipping the current element
    int nonPick = 0 + func(ind - 1, arr, dp);  

    /* Store the result in dp 
    array and return the maximum */
    return dp[ind] = max(pick, nonPick);
}
public:
    /*Function to calculate the maximum
    sum of nonAdjacent elements d*/
    int nonAdjacent(vector<int>& nums) {
        int ind = nums.size()-1;
        
        //Initialize the dp array with -1
        vector<int> dp(ind+1, -1);
        
        //Return the maximum sum
        return func(ind, nums, dp);
    }
};

int main() {
    vector<int> arr{2, 1, 4, 9};
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the solve function and print the result
    cout << sol.nonAdjacent(arr);

    return 0;
}
import java.util.*;

class Solution {
    // Function to solve the problem using memoization
    private int func(int ind, int[] arr, int[] dp) {
        // Base cases
        if (ind == 0)
            return arr[ind];
        if (ind < 0)
            return 0;

        /* Check if the result for 'ind'
        has already been computed*/
        if (dp[ind] != -1)
            return dp[ind];

        // Choosing the current element
        int pick = arr[ind] + func(ind - 2, arr, dp);

        // Skipping the current element
        int nonPick = func(ind - 1, arr, dp);

        /* Store the result in dp 
        array and return the maximum */
        return dp[ind] = Math.max(pick, nonPick);
    }

    /* Function to calculate the maximum
    sum of non-adjacent elements */
    public int nonAdjacent(int[] nums) {
        int ind = nums.length - 1;

        // Initialize the dp array with -1
        int[] dp = new int[ind + 1];
        Arrays.fill(dp, -1);

        // Return the maximum sum
        return func(ind, nums, dp);
    }

    public static void main(String[] args) {
        int[] arr = {2, 1, 4, 9};

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the nonAdjacent function and print the result
        System.out.println(sol.nonAdjacent(arr));
    }
}
class Solution:
    # Function to solve the problem using memoization
    def func(self, ind, arr, dp):
        # Base cases
        if ind == 0:
            return arr[ind]
        if ind < 0:
            return 0

        """ Check if the result for 'ind'
        has already been computed"""
        if dp[ind] != -1:
            return dp[ind]

        # Choosing the current element
        pick = arr[ind] + self.func(ind - 2, arr, dp)

        # Skipping the current element
        nonPick = self.func(ind - 1, arr, dp)

        """ Store the result in dp 
        array and return the maximum"""
        dp[ind] = max(pick, nonPick)
        return dp[ind]

    """ Function to calculate the maximum
    sum of non-adjacent elements """
    def nonAdjacent(self, nums):
        ind = len(nums) - 1

        # Initialize the dp array with -1
        dp = [-1] * (ind + 1)

        # Return the maximum sum
        return self.func(ind, nums, dp)

if __name__ == "__main__":
    arr = [2, 1, 4, 9]

    # Create an instance of Solution class
    sol = Solution()

    # Call the nonAdjacent function and print the result
    print(sol.nonAdjacent(arr))
class Solution {
    // Function to solve the problem using memoization
    func(ind, arr, dp) {
        // Base cases
        if (ind === 0) {
            return arr[ind];
        }
        if (ind < 0) {
            return 0;
        }

        /* Check if the result for 'ind'
        has already been computed */
        if (dp[ind] !== -1) {
            return dp[ind];
        }

        // Choosing the current element
        let pick = arr[ind] + this.func(ind - 2, arr, dp);

        // Skipping the current element
        let nonPick = this.func(ind - 1, arr, dp);

        /* Store the result in dp 
        array and return the maximum */
        dp[ind] = Math.max(pick, nonPick);
        return dp[ind];
    }

    /*Function to calculate the maximum
    sum of non-adjacent elements*/
    nonAdjacent(nums) {
        let ind = nums.length - 1;

        // Initialize the dp array with -1
        let dp = new Array(ind + 1).fill(-1);

        // Return the maximum sum
        return this.func(ind, nums, dp);
    }
}
    let arr = [2, 1, 4, 9];

    // Create an instance of Solution class
    let sol = new Solution();

    // Call the nonAdjacent function and print the result
    console.log(sol.nonAdjacent(arr));

Complexity Analysis:

Time Complexity: O(N), where N is the given size of array. The overlapping subproblems will return the answer in constant time O(1). As total subproblems can be at max N. Therefore it will take O(N).

Space Complexity:O(N) + O(N), As stack space of O(N) and an dp array O(N) is used. Therefore total space complexity will be O(N) + O(N) ≈ O(N)

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare an Array dp[] of Size n: Here, n is the size of the array provided as input. It represents the solution to the subproblem for any given index.

Setting Base Cases in the Array: In the recursive code, we knew the answer for base case, when 'ind' = 0, Here, dp[0] is initialized directly to arr[0] because if there is only one element in the array, that element itself is the maximum sum.

Iterative Computation Using a Loop: Set an iterative loop that traverses the array( from index 1 to n-1). To compute the solution for larger values, use a loop that iterates from the smallest subproblem up to n-1.

Explanation of dp[i] Calculation: The current value(dp[i]) represents the subproblem and by the recurrence relation it is obvious that dp[i] is calculated by either picking the current element or not picking it (dp[i-2] + arr[i] and dp[i-1]))

Choosing the maximum: Update dp[i] to store the maximum of these two values pick and nonPick.

Returning the last element: The last element of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /*Function to calculate the maximum
    sum of nonAdjacent elements*/
    int nonAdjacent(vector<int> &nums) {
        int ind = nums.size();
        vector<int> dp(ind, 0);
        
        // Base case
        dp[0] = nums[0];

        // Iterate through the elements of the array
        for (int i = 1; i < ind; i++) {
            
            /* Calculate maximum value by either picking
            the current element or not picking it*/
            int pick = nums[i];
            if (i > 1)
                pick += dp[i - 2];
            int nonPick = dp[i - 1];

            // Store the maximum value in dp array
            dp[i] = max(pick, nonPick);
        }

        /* The last element of the dp array
        will contain the maximum sum*/
        return dp[ind-1];
    }
};

int main() {
    vector<int> arr {2,1,4,9};

    //Create an instance of Solution class
    Solution sol;

    // Call the solve function and print the result
    cout << sol.nonAdjacent(arr);

    return 0;
}
import java.util.*;

class Solution {
    /* Function to calculate the maximum
    sum of nonAdjacent elements */
    public int nonAdjacent(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        
        // Base case
        dp[0] = nums[0];

        // Iterate through the elements of the array
        for (int i = 1; i < n; i++) {
            
            /* Calculate maximum value by either picking
            the current element or not picking it */
            int pick = nums[i];
            if (i > 1)
                pick += dp[i - 2];
            int nonPick = dp[i - 1];

            // Store the maximum value in dp array
            dp[i] = Math.max(pick, nonPick);
        }

        /* The last element of the dp array
        will contain the maximum sum */
        return dp[n - 1];
    }

    public static void main(String[] args) {
        int[] arr = {2, 1, 4, 9};

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the solve function and print the result
        System.out.println(sol.nonAdjacent(arr));
    }
}
class Solution:
    """ Function to calculate the maximum
    sum of nonAdjacent elements """
    def nonAdjacent(self, nums):
        n = len(nums)
        dp = [0] * n
        
        # Base case
        dp[0] = nums[0]

        # Iterate through the elements of the array
        for i in range(1, n):
            
            """ Calculate maximum value by either picking
            the current element or not picking it"""
            pick = nums[i]
            if i > 1:
                pick += dp[i - 2]
            nonPick = dp[i - 1]

            # Store the maximum value in dp array
            dp[i] = max(pick, nonPick)

        """ The last element of the dp array
        will contain the maximum sum"""
        return dp[-1]

arr = [2, 1, 4, 9]

#Create an instance of Solution class
sol = Solution()

#Print the answer
print(sol.nonAdjacent(arr))
class Solution {
    /* Function to calculate the maximum
    sum of nonAdjacent elements*/
    nonAdjacent(nums) {
        let n = nums.length;
        let dp = new Array(n).fill(0);
        
        // Base case
        dp[0] = nums[0];

        // Iterate through the elements of the array
        for (let i = 1; i < n; i++) {
            
            /* Calculate maximum value by either picking
            the current element or not picking it*/
            let pick = nums[i];
            if (i > 1)
                pick += dp[i - 2];
            let nonPick = dp[i - 1];

            // Store the maximum value in dp array
            dp[i] = Math.max(pick, nonPick);
        }

        /* The last element of the dp array
        will contain the maximum sum*/
        return dp[n - 1];
    }
}

let arr = [2, 1, 4, 9];

//Create an instance of Solution class
let sol = new Solution();

//Print the answer
console.log(sol.nonAdjacent(arr));

Complexity Analysis:

Time Complexity: O(N), where N is the given size of array. As each element of the array is processed exactly once in a single pass.

Space Complexity:O(N), as an additional dp array is used, which stores results for each element of the array.

If we do some observation, we find that the values required at every iteration for dp[i] are dp[i-1] and dp[i-2]. we see that for any i, we do need only the last two values in the array. So is there is no need to maintain a whole array for it.

Let us call dp[i-1] as prev and dp[i-2] as prev2. Now understand the following illustration:

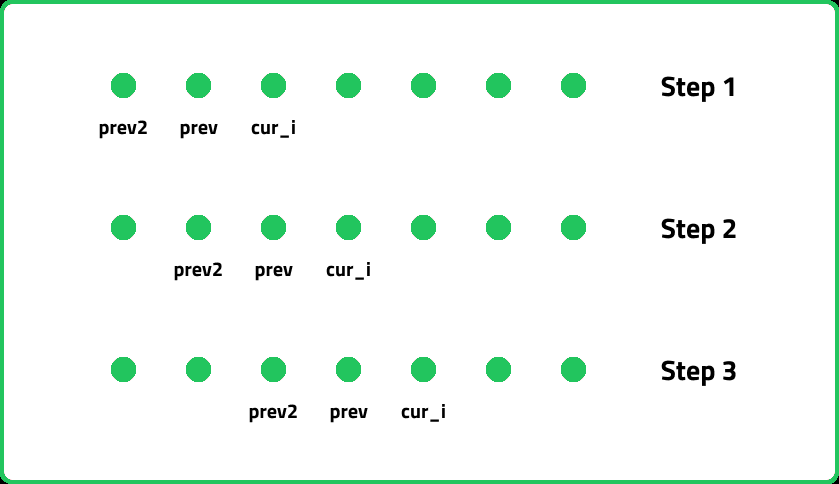
Each iteration cur_i and prev become the next iteration’s prev and prev2 respectively. Therefore after calculating cur_i, if we update prev and prev2 according to the next step, we will always get the answer.

After the iterative loop has ended we can simply return prev as our answer. As at the end of the loop prev will contain curr_i, the maximum sum.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /*Function to calculate the maximum
    sum of nonAdjacent elements*/
    int nonAdjacent(vector<int> &nums) {
        int n = nums.size();
        int prev = nums[0];   
        int prev2 = 0;       
    
        for (int i = 1; i < n; i++) {
            // Maximum sum if we pick current element
            int pick = nums[i];  
            
            if (i > 1){
                //Add the maximum sum two elements ago
                pick += prev2;  
            }
            // Maximum sum if we don't pick current element
            int nonPick = 0 + prev;  
            
            // Maximum at the current element
            int cur_i = max(pick, nonPick); 
            
            prev2 = prev;   
            prev = cur_i;    
        }
        // Return the maximum sum
        return prev;  
    }
};

int main() {
    vector<int> arr {2,1,4,9};

    //Create an instance of Solution class
    Solution sol;

    // Call the solve function and print the result
    cout << sol.nonAdjacent(arr);

    return 0;
}
import java.util.*;

class Solution {
    /* Function to calculate the maximum
    sum of nonAdjacent elements*/
    public int nonAdjacent(int[] nums) {
        int n = nums.length;
        int prev = nums[0];
        int prev2 = 0;

        for (int i = 1; i < n; i++) {
            // Maximum sum if we pick current element
            int pick = nums[i];
            
            if (i > 1) {
                // Add the maximum sum two elements ago
                pick += prev2;
            }
            // Maximum sum if we don't pick current element
            int nonPick = 0 + prev;

            // Maximum at the current element
            int cur_i = Math.max(pick, nonPick);

            prev2 = prev;
            prev = cur_i;
        }
        // Return the maximum sum
        return prev;
    }

    public static void main(String[] args) {
        int[] arr = {2, 1, 4, 9};

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the solve function and print the result
        System.out.println(sol.nonAdjacent(arr));
    }
}
class Solution:
    """Function to calculate the maximum 
    sum of nonAdjacent elements"""
    def nonAdjacent(self, nums):
        n = len(nums)
        prev = nums[0]
        prev2 = 0

        for i in range(1, n):
            # Maximum sum if we pick current element
            pick = nums[i]

            if i > 1:
                # Add the maximum sum two elements ago
                pick += prev2
            # Maximum sum if we don't pick current element
            nonPick = 0 + prev

            # Maximum at the current element
            cur_i = max(pick, nonPick)

            prev2 = prev
            prev = cur_i

        # Return the maximum sum
        return prev

arr = [2, 1, 4, 9]

#Create an instance of Solution class
sol = Solution()

#Print the answer
print(sol.nonAdjacent(arr))
class Solution {
    /* Function to calculate the maximum
    sum of nonAdjacent elements */
    nonAdjacent(nums) {
        let n = nums.length;
        let prev = nums[0];
        let prev2 = 0;

        for (let i = 1; i < n; i++) {
            // Maximum sum if we pick current element
            let pick = nums[i];

            if (i > 1) {
                // Add the maximum sum two elements ago
                pick += prev2;
            }
            // Maximum sum if we don't pick current element
            let nonPick = 0 + prev;

            // Maximum at the current element
            let cur_i = Math.max(pick, nonPick);

            prev2 = prev;
            prev = cur_i;
        }
        // Return the maximum sum
        return prev;
    }
}

let arr = [2, 1, 4, 9];

//Create an instance of Solution class
let sol = new Solution();

//Print the solution 
console.log(sol.nonAdjacent(arr));

Complexity Analysis:

Time Complexity: O(N), where N is the given size of array. As each element of the array is processed exactly once in a single pass.

Space Complexity:O(1), as there is no extra space used.

Frequently Occurring Doubts

Q: Can we solve this problem using a greedy approach?

A: No, a greedy approach (always taking the largest available element) fails because it doesn’t consider future consequences (e.g., picking a large element might force skipping multiple good elements).

Q: Why is the recurrence relation based on dp[i-1] and dp[i-2]?

A: If we include nums[i], we must take dp[i-2] to ensure no adjacent elements are included. If we exclude nums[i], we take dp[i-1] to get the best sum without nums[i].

Interview Followup Questions

Q: What if there was an additional constraint that elements can only be picked if their value is even?

A: Instead of considering all elements, apply the same DP approach only to even numbers.

Q: What if the elements were arranged in a circular array (first and last elements are adjacent)?

A: This modifies the problem into the circular house robber problem, where we solve for two cases: Exclude the first element and solve normally. Exclude the last element and solve normally. Return the maximum of both cases.

Notes

Your notes are automatically saved in your browser's local storage and will persist across sessions on this device.

Problem Categories

Maximum sum of non adjacent elements

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form recursive solution:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code

Facts