Unique paths II
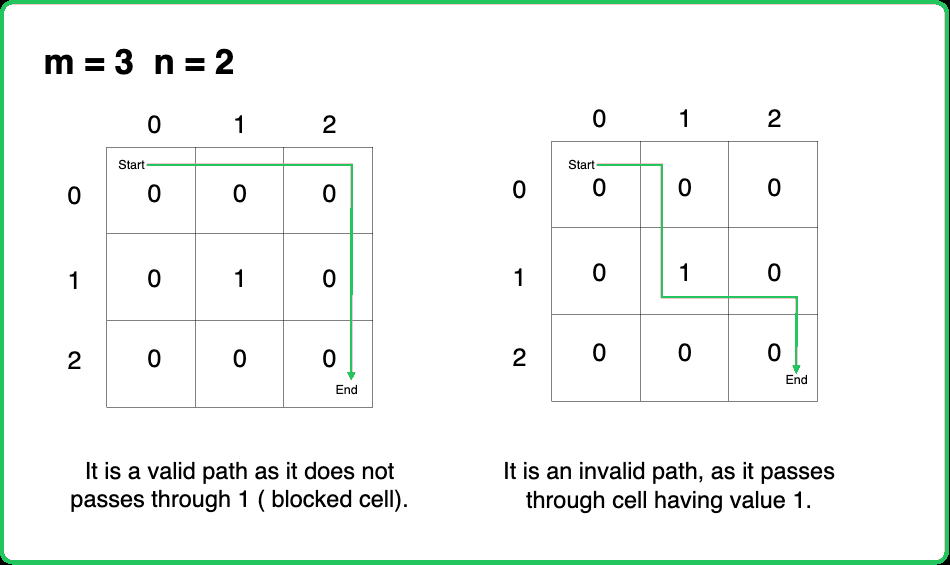
Given an m x n 2d array named matrix, where each cell is either 0 or 1. Return the number of unique ways to go from the top-left cell (matrix[0][0]) to the bottom-right cell (matrix[m-1][n-1]). A cell is blocked if its value is 1, and no path is possible through that cell.
Movement is allowed in only two directions from a cell - right and bottom.
Examples:
Input: matrix = [[0, 0, 0], [0, 1, 0], [0, 0, 0]]
Output: 2
Explanation: The two possible paths are:
1) down -> down-> right -> right
2) right -> right -> down -> down
Input: matrix = [[0, 0, 0], [0, 0, 1], [0, 1, 0]]
Output: 0
Explanation: There is no way to reach the bottom-right cell.
Input: matrix = [[0, 0, 0, 0], [0, 0, 1, 0]]
Constraints
- m == number of rows in matrix
- n == number of columns in matrix
- 1 <= n, m <= 100
- Value of each cell in matrix is either 0 or 1
- The answer will not exceed 109
Hints
- "Let dp[i][j] represent the number of ways to reach cell (i, j). If matrix[i][j] == 1, the cell is blocked, so dp[i][j] = 0."
- "A recursive approach without memoization results in exponential time complexity (O(2^{m+n})), making it inefficient for large grids. Using dynamic programming (O(m*n)), we store computed results in dp[][] to avoid redundant calculations."
Company Tags
Editorial
As we have to count all the unique ways possible to go from matrix[0,0] (top-left)to matrix[m-1,n-1](bottom-right) by only moving through the cells which have value as '0', we can try recursion to generate all possible paths and return the count of them.
Steps to form the recursive solution:
We will be solving the problem in top-down manner, so f(i,j) will return total unique paths from (i,j) to (0,0) by only moving through cells having value '0', therefore at every index, we will try to move up and towards the left. Here f(i,j) represents a subproblem.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(i,j){
//Base case
up = f(i-1, j)
left = f(i, j-1)
}/*It is pseudocode and it is not tied to
any specific programming language*/
f(i,j){
//Base case
up = f(i-1, j)
left = f(i, j-1)
return up+left
}When i>0 and j>0 and mat[i][j] = 1, it means that the current cell is an obstacle, so we can’t find a path from here. Therefore, we return 0.
When i=0 and j=0, that is we have reached the destination so we can count the current path that is going on, hence we return 1.
When i<0 and j<0, it means that we have crossed the boundary of the matrix and we couldn’t find a right path, hence we return 0.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(i,j){
if(i > 0 && j> 0 && mat[i][j] == 1) return 0
if(i == 0 && j == 0) return 1
if(i < 0 || j < 0) return 0
}#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
//Function to solve the problem using recursion
int func(int i, int j, vector<vector<int>>& matrix){
// Base case
if (i == 0 && j == 0) return 1;
if(i > 0 && j > 0 && matrix[i][j] == 1) return 0;
if(i < 0 || j < 0) return 0;
/* Calculate the number of ways by
moving up and left recursively.*/
int up = func(i - 1, j, matrix);
int left = func(i, j - 1, matrix);
// Return the total ways
return up + left;
}
public:
/*Function to find all unique paths to reach
matrix[m-1][n-1] form matrix[0][0] with obstacles*/
int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
//Return the total number of paths
return func(m-1, n-1, matrix);
}
};
int main() {
vector<vector<int>> maze{
{0, 0, 0},
{0, 1, 0},
{0, 0, 0}
};
//Create an instance of Solution class
Solution sol;
cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
return 0;
}
import java.util.*;
class Solution {
// Function to solve the problem using recursion
private int func(int i, int j, int[][] matrix) {
// Base case
if (i == 0 && j == 0) return 1;
if (i > 0 && j > 0 && matrix[i][j] == 1) return 0;
if (i < 0 || j < 0) return 0;
/* Calculate the number of ways by
moving up and left recursively.*/
int up = func(i - 1, j, matrix);
int left = func(i, j - 1, matrix);
// Return the total ways
return up + left;
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
public int uniquePathsWithObstacles(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
// Return the total number of paths
return func(m - 1, n - 1, matrix);
}
public static void main(String[] args) {
int[][] maze = {
{0, 0, 0},
{0, 1, 0},
{0, 0, 0}
};
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("Number of paths with obstacles: " + sol.uniquePathsWithObstacles(maze));
}
}
class Solution:
# Function to solve the problem using recursion
def func(self, i, j, matrix):
# Base case
if i == 0 and j == 0:
return 1
if i > 0 and j > 0 and matrix[i][j] == 1:
return 0
if i < 0 or j < 0:
return 0
""" Calculate the number of ways by
moving up and left recursively."""
up = self.func(i - 1, j, matrix)
left = self.func(i, j - 1, matrix)
# Return the total ways
return up + left
""" Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles"""
def uniquePathsWithObstacles(self, matrix):
m = len(matrix)
n = len(matrix[0])
# Return the total number of paths
return self.func(m - 1, n - 1, matrix)
if __name__ == "__main__":
maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
]
# Create an instance of Solution class
sol = Solution()
print("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze))
class Solution {
// Function to solve the problem using recursion
func(i, j, matrix) {
// Base case
if (i === 0 && j === 0) return 1;
if (i > 0 && j > 0 && matrix[i][j] === 1) return 0;
if (i < 0 || j < 0) return 0;
/* Calculate the number of ways by
moving up and left recursively.*/
let up = this.func(i - 1, j, matrix);
let left = this.func(i, j - 1, matrix);
// Return the total ways
return up + left;
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
uniquePathsWithObstacles(matrix) {
let m = matrix.length;
let n = matrix[0].length;
// Return the total number of paths
return this.func(m - 1, n - 1, matrix);
}
}
let maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
];
// Create an instance of Solution class
let sol = new Solution();
console.log("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze));
Complexity Analysis:
Time Complexity: O(2(M+N)*(M+N)), where M is the number of row and N is the number of column in 2D array. As, each cell has 2 choices and path length is near about (M+N) and each path would take (M+N) to travel as well.Space Complexity:O((M-1)+(N-1)), In the worst case, the depth of the recursion can reach (M-1)+(N-1), corresponding to the maximum number of steps required to reduce both i and j to 0.
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
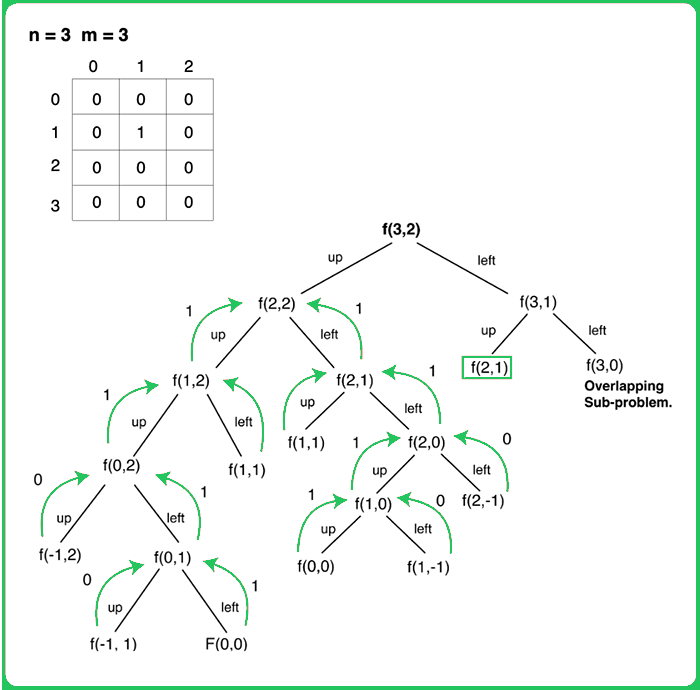
In order to convert a recursive solution to memoization the following steps will be taken:
The dp array stores the calculations of subproblems, dp[i][j] represents the total ways to reach (0,0) from (i,j)Initially, fill the array with -1, to indicate that no subproblem has been solved yet.
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
//Function to solve the problem using memoization
int func(int i, int j, vector<vector<int>>& matrix, vector<vector<int>> &dp){
// Base cases
if (i < 0 || j < 0 || matrix[i][j] == 1) return 0;
else if(i == 0 && j == 0) return 1;
// If the result is already computed, return it
if(dp[i][j] != -1) return dp[i][j];
/* Calculate the number of ways by
moving up and left recursively.*/
int up = func(i - 1, j, matrix, dp);
int left = func(i, j - 1, matrix, dp);
// Return the total ways
return dp[i][j] = up + left;
}
public:
/*Function to find all unique paths to reach
matrix[m-1][n-1] form matrix[0][0] with obstacles*/
int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
// Initialize DP table to memoize results
vector<vector<int>> dp(m, vector<int>(n, -1));
//Return the total number of paths
return func(m-1, n-1, matrix, dp);
}
};
int main() {
vector<vector<int>> maze{
{0, 0, 0},
{0, 1, 0},
{0, 0, 0}
};
//Create an instance of Solution class
Solution sol;
cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
return 0;
}
import java.util.*;
class Solution {
private int func(int i, int j, int[][] matrix, int[][] dp) {
// Base cases
if (i < 0 || j < 0 || matrix[i][j] == 1) return 0;
else if (i == 0 && j == 0) return 1;
// If the result is already computed, return it
if (dp[i][j] != -1) return dp[i][j];
/* Calculate the number of ways by
moving up and left recursively. */
int up = func(i - 1, j, matrix, dp);
int left = func(i, j - 1, matrix, dp);
// Return the total ways
return dp[i][j] = up + left;
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles */
public int uniquePathsWithObstacles(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
// Initialize DP table to memoize results
int[][] dp = new int[m][n];
for (int[] row : dp) Arrays.fill(row, -1);
// Return the total number of paths
return func(m - 1, n - 1, matrix, dp);
}
}
class Main {
public static void main(String[] args) {
int[][] maze = {
{0, 0, 0},
{0, 1, 0},
{0, 0, 0}
};
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("Number of paths with obstacles: " + sol.uniquePathsWithObstacles(maze));
}
}
class Solution:
def func(self, i, j, matrix, dp):
# Base cases
if i < 0 or j < 0 or matrix[i][j] == 1:
return 0
elif i == 0 and j == 0:
return 1
# If the result is already computed, return it
if dp[i][j] != -1:
return dp[i][j]
""" Calculate the number of ways by
moving up and left recursively. """
up = self.func(i - 1, j, matrix, dp)
left = self.func(i, j - 1, matrix, dp)
# Return the total ways
dp[i][j] = up + left
return dp[i][j]
""" Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles """
def uniquePathsWithObstacles(self, matrix):
m, n = len(matrix), len(matrix[0])
# Initialize DP table to memoize results
dp = [[-1] * n for _ in range(m)]
# Return the total number of paths
return self.func(m - 1, n - 1, matrix, dp)
if __name__ == "__main__":
maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
]
# Create an instance of Solution class
sol = Solution()
print("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze))
class Solution {
func(i, j, matrix, dp) {
// Base cases
if (i < 0 || j < 0 || matrix[i][j] === 1) return 0;
else if (i === 0 && j === 0) return 1;
// If the result is already computed, return it
if (dp[i][j] !== -1) return dp[i][j];
/* Calculate the number of ways by
moving up and left recursively. */
let up = this.func(i - 1, j, matrix, dp);
let left = this.func(i, j - 1, matrix, dp);
// Return the total ways
return (dp[i][j] = up + left);
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles */
uniquePathsWithObstacles(matrix) {
let m = matrix.length;
let n = matrix[0].length;
// Initialize DP table to memoize results
let dp = Array.from({ length: m }, () => Array(n).fill(-1));
// Return the total number of paths
return this.func(m - 1, n - 1, matrix, dp);
}
}
// Main execution
const maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
];
// Create an instance of Solution class
const sol = new Solution();
console.log("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze));
Complexity Analysis:
Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. At max, there will be M*N calls of recursion as the subproblems can go upto M*N.Space Complexity:O((N-1)+(M-1)) + O(M*N), We are using a recursion stack space: O((N-1)+(M-1)), here (N-1)+(M-1) is the path length and an external DP Array of size ‘M*N’.
Tabulation is the bottom-up approach, which means we will go from the base case to the main problem. In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
Whenever i>0 , j>0 and mat[i][j]==1, we will simply mark dp[i][j] = 0, it means that this cell is a blocked one and no path is possible through it.
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to solve the problem using tabulation
int func(int m, int n, vector<vector<int>>& matrix, vector<vector<int>>& dp) {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// Base conditions
if (matrix[i][j] == 1) {
/* If there's an obstacle at the
cell, no paths can pass through it*/
dp[i][j] = 0;
continue;
}
if (i == 0 && j == 0) {
/* If we are at the starting
point, there is one path to it*/
dp[i][j] = 1;
continue;
}
int up = 0;
int left = 0;
/* Check if we can move up and left
(if not at the edge of the maze)*/
if (i > 0)
up = dp[i - 1][j];
if (j > 0)
left = dp[i][j - 1];
/* Total number of paths to reach (i, j)
is the sum of paths from above and left*/
dp[i][j] = up + left;
}
}
/* The final result is stored in dp[m-1][n-1],
which represents the destination*/
return dp[m - 1][n - 1];
}
public:
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
// Initialize DP table to memoize results
vector<vector<int>> dp(m, vector<int>(n, 0));
// Return the total number of paths
return func(m, n, matrix, dp);
}
};
int main() {
vector<vector<int>> maze{
{0, 0, 0},
{0, 1, 0},
{0, 0, 0}
};
// Create an instance of Solution class
Solution sol;
cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
return 0;
}
class Solution {
// Function to solve the problem using tabulation
private int func(int m, int n, int[][] matrix, int[][] dp) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// Base conditions
if (matrix[i][j] == 1) {
/* If there's an obstacle at the
cell, no paths can pass through it*/
dp[i][j] = 0;
continue;
}
if (i == 0 && j == 0) {
/* If we are at the starting
point, there is one path to it*/
dp[i][j] = 1;
continue;
}
int up = 0;
int left = 0;
/* Check if we can move up and left
(if not at the edge of the maze)*/
if (i > 0)
up = dp[i - 1][j];
if (j > 0)
left = dp[i][j - 1];
/* Total number of paths to reach (i, j)
is the sum of paths from above and left*/
dp[i][j] = up + left;
}
}
/* The final result is stored in dp[n-1][m-1],
which represents the destination*/
return dp[n - 1][m - 1];
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
public int uniquePathsWithObstacles(int[][] matrix) {
int m = matrix[0].length;
int n = matrix.length;
// Initialize DP table to memoize results
int[][] dp = new int[n][m];
// Return the total number of paths
return func(m, n, matrix, dp);
}
public static void main(String[] args) {
int[][] maze = {
{0, 0, 0},
{0, 1, 0},
{0, 0, 0}
};
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("Number of paths with obstacles: " + sol.uniquePathsWithObstacles(maze));
}
}
class Solution:
# Function to solve the problem using tabulation
def func(self, m, n, matrix, dp):
for i in range(n):
for j in range(m):
# Base conditions
if matrix[i][j] == 1:
""" If there's an obstacle at the
cell, no paths can pass through it"""
dp[i][j] = 0
continue
if i == 0 and j == 0:
""" If we are at the starting
point, there is one path to it"""
dp[i][j] = 1
continue
up = 0
left = 0
""" Check if we can move up and left
(if not at the edge of the maze)"""
if i > 0:
up = dp[i - 1][j]
if j > 0:
left = dp[i][j - 1]
""" Total number of paths to reach (i, j)
is the sum of paths from above and left"""
dp[i][j] = up + left
""" The final result is stored in dp[n-1][m-1],
which represents the destination"""
return dp[n - 1][m - 1]
""" Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles"""
def uniquePathsWithObstacles(self, matrix):
m = len(matrix[0])
n = len(matrix)
# Initialize DP table to memoize results
dp = [[0] * m for _ in range(n)]
# Return the total number of paths
return self.func(m, n, matrix, dp)
if __name__ == "__main__":
maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
]
# Create an instance of Solution class
sol = Solution()
print("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze))
class Solution {
// Function to solve the problem using tabulation
func(m, n, matrix, dp) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
// Base conditions
if (matrix[i][j] === 1) {
/* If there's an obstacle at the
cell, no paths can pass through it*/
dp[i][j] = 0;
continue;
}
if (i === 0 && j === 0) {
/* If we are at the starting
point, there is one path to it*/
dp[i][j] = 1;
continue;
}
let up = 0;
let left = 0;
/* Check if we can move up and left
(if not at the edge of the maze)*/
if (i > 0)
up = dp[i - 1][j];
if (j > 0)
left = dp[i][j - 1];
/* Total number of paths to reach (i, j)
is the sum of paths from above and left*/
dp[i][j] = up + left;
}
}
/* The final result is stored in dp[n-1][m-1],
which represents the destination*/
return dp[n - 1][m - 1];
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
uniquePathsWithObstacles(matrix) {
const m = matrix[0].length;
const n = matrix.length;
// Initialize DP table to memoize results
const dp = new Array(n).fill(0).map(() => new Array(m).fill(0));
// Return the total number of paths
return this.func(m, n, matrix, dp);
}
}
const maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
];
// Create an instance of Solution class
const sol = new Solution();
console.log("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze));
Complexity Analysis:
Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.Space Complexity:O(M*N), As an external DP Array of size ‘M*N’ is used to store the intermediate calculations.
If we closely look at the relationship obltained in the tabulation approach, dp[i][j] = dp[i-1][j] + dp[i][j-1]), we see that we only need the previous row and column, in order to calculate dp[i][j]. Therefore we can space optimize it.
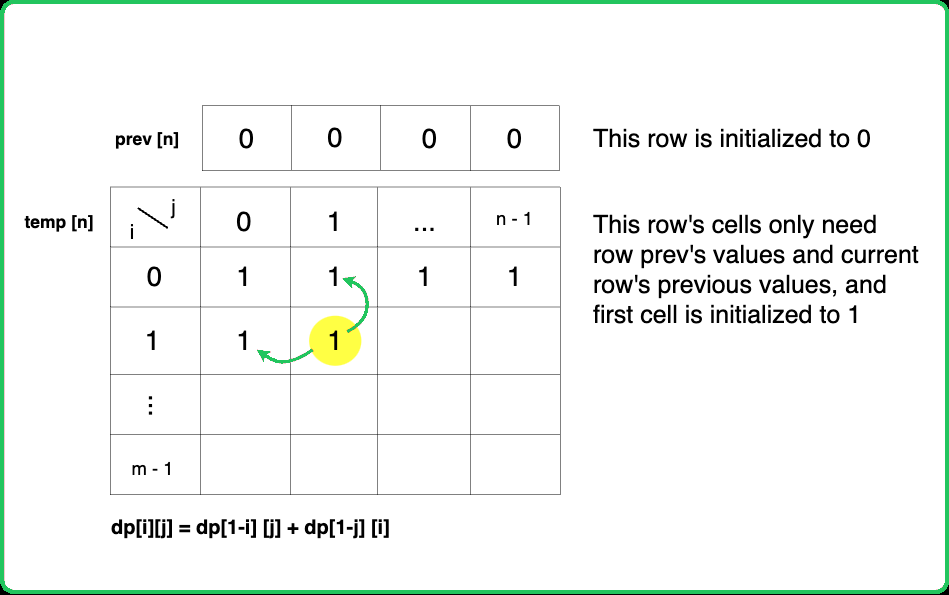
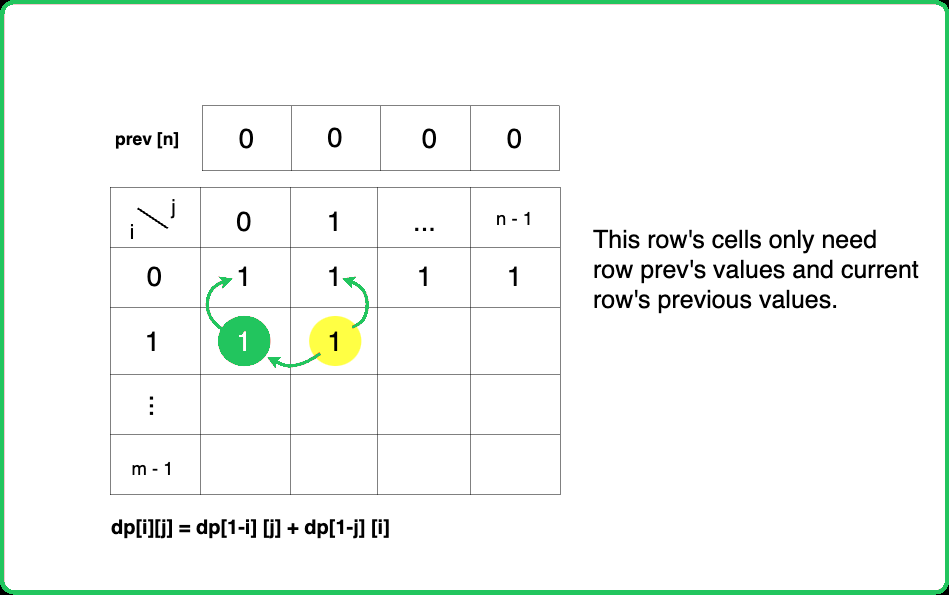
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to solve the problem using space optimization
int func(int m, int n, vector<vector<int>>& matrix) {
/* Initialize a vector to store
the previous row's path counts*/
vector<int> prev(n, 0);
for (int i = 0; i < m; i++) {
/* Initialize a temporary
vector for the current row*/
vector<int> temp(n, 0);
for (int j = 0; j < n; j++) {
// Base conditions
if (i > 0 && j > 0 && matrix[i][j] == 1) {
/* If there's an obstacle at (i, j),
no paths can pass through it*/
temp[j] = 0;
continue;
}
if (i == 0 && j == 0) {
/* If we are at the starting
point, there is one path to it*/
temp[j] = 1;
continue;
}
int up = 0;
int left = 0;
/* Check if we can move up and left
(if not at the edge of the maze)*/
if (i > 0)
up = prev[j];
if (j > 0)
left = temp[j - 1];
/* Total number of paths to reach (i, j)
is the sum of paths from above and left*/
temp[j] = up + left;
}
// Update the previous row with the current row
prev = temp;
}
/* The final result is stored in prev[m-1], which
represents the destination in the last row*/
return prev[n - 1];
}
public:
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
int uniquePathsWithObstacles(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
// Return the total number of paths
return func(m, n, matrix);
}
};
int main() {
vector<vector<int>> maze{
{0, 0, 0},
{0, 1, 0},
{0, 0, 0},
};
// Create an instance of Solution class
Solution sol;
cout << "Number of paths with obstacles: " << sol.uniquePathsWithObstacles(maze) << endl;
return 0;
}
import java.util.*;
class Solution {
// Function to solve the problem using space optimization
private int func(int m, int n, int[][] matrix) {
/* Initialize a vector to store
the previous row's path counts*/
int[] prev = new int[n];
for (int i = 0; i < m; i++) {
/* Initialize a temporary
vector for the current row*/
int[] temp = new int[n];
for (int j = 0; j < n; j++) {
// Base conditions
if (i > 0 && j > 0 && matrix[i][j] == 1) {
/* If there's an obstacle at (i, j),
no paths can pass through it*/
temp[j] = 0;
continue;
}
if (i == 0 && j == 0) {
/* If we are at the starting
point, there is one path to it*/
temp[j] = 1;
continue;
}
int up = 0;
int left = 0;
/* Check if we can move up and left
(if not at the edge of the maze)*/
if (i > 0)
up = prev[j];
if (j > 0)
left = temp[j - 1];
/* Total number of paths to reach (i, j)
is the sum of paths from above and left*/
temp[j] = up + left;
}
// Update the previous row with the current row
prev = temp;
}
/* The final result is stored in prev[n-1], which
represents the destination in the last row*/
return prev[n - 1];
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
public int uniquePathsWithObstacles(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
// Return the total number of paths
return func(m, n, matrix);
}
public static void main(String[] args) {
int[][] maze = {
{0, 0, 0},
{0, 1, 0},
{0, 0, 0}
};
// Create an instance of Solution class
Solution sol = new Solution();
System.out.println("Number of paths with obstacles: " + sol.uniquePathsWithObstacles(maze));
}
}
class Solution:
# Function to solve the problem using space optimization
def func(self, m, n, matrix):
""" Initialize a vector to store
the previous row's path counts"""
prev = [0] * n
for i in range(m):
# Initialize a temporary vector for the current row
temp = [0] * n
for j in range(n):
# Base conditions
if i > 0 and j > 0 and matrix[i][j] == 1:
""" If there's an obstacle at (i, j),
no paths can pass through it"""
temp[j] = 0
continue
if i == 0 and j == 0:
""" If we are at the starting
point, there is one path to it"""
temp[j] = 1
continue
up = 0
left = 0
""" Check if we can move up and left
(if not at the edge of the maze)"""
if i > 0:
up = prev[j]
if j > 0:
left = temp[j - 1]
""" Total number of paths to reach (i, j)
is the sum of paths from above and left"""
temp[j] = up + left
# Update the previous row with the current row
prev = temp
""" The final result is stored in prev[n-1], which
represents the destination in the last row"""
return prev[n - 1]
""" Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles"""
def uniquePathsWithObstacles(self, matrix):
m = len(matrix)
n = len(matrix[0])
# Return the total number of paths
return self.func(m, n, matrix)
if __name__ == "__main__":
maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
]
# Create an instance of Solution class
sol = Solution()
print("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze))
class Solution {
// Function to solve the problem using space optimization
func(m, n, matrix) {
/*Initialize a vector to store
the previous row's path counts*/
let prev = new Array(n).fill(0);
for (let i = 0; i < m; i++) {
// Initialize a temporary vector for current row
let temp = new Array(n).fill(0);
for (let j = 0; j < n; j++) {
// Base conditions
if (i > 0 && j > 0 && matrix[i][j] === 1) {
/* If there's an obstacle at (i, j),
no paths can pass through it*/
temp[j] = 0;
continue;
}
if (i === 0 && j === 0) {
/* If we are at the starting
pont, there is one path to it*/
temp[j] = 1;
continue;
}
let up = 0;
let left = 0;
/* Check if we can move up and left
(if not at the edge of the maze)*/
if (i > 0)
up = prev[j];
if (j > 0)
left = temp[j - 1];
/* Total number of paths to reach (i, j)
is the sum of paths from above and left*/
temp[j] = up + left;
}
// Update the previous row with the current row
prev = temp;
}
/* The final result is stored in prev[n-1], which
represents the destination in the last row*/
return prev[n - 1];
}
/* Function to find all unique paths to reach
matrix[m-1][n-1] from matrix[0][0] with obstacles*/
uniquePathsWithObstacles(matrix) {
const m = matrix.length;
const n = matrix[0].length;
// Return the total number of paths
return this.func(m, n, matrix);
}
}
const maze = [
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
];
// Create an instance of Solution class
const sol = new Solution();
console.log("Number of paths with obstacles:", sol.uniquePathsWithObstacles(maze));
Complexity Analysis:
Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.Space Complexity:O(N), We are using an external array of size ‘N’ to store only one row.
Frequently Occurring Doubts
Q: Can a greedy approach work?
A: No, because choosing the right or down direction optimally at each step does not guarantee a globally optimal path.
Q: Can we use the combinatorial approach (O(1)) like in the standard unique paths problem?
A: No, because obstacles break the uniform structure, making combinatorial formulas ineffective.
Interview Followup Questions
Q: How would you modify this for a grid with negative weight penalties instead of binary blocks?
A: Use Dijkstra’s algorithm or Bellman-Ford algorithm to find the shortest path cost.
Q: What if the grid had teleportation cells (T) that allowed instant movement?
A: Modify dp[i][j] to track jumps, incorporating teleportation paths dynamically.
Notes
Code
2
0
1
Facts
- • The underlying concept of this problem is extensively used in navigation and mapping services like Google Maps and GPS devices
- • Algorithms that solve similar pathfinding problems, like the A* algorithm, are designed to calculate the shortest route between two points
- • They consider obstacles (like blocked roads or traffic) by using a similar concept as the "1s" in the provided problem
- • Essentially, these algorithms navigate through a complex 2D grid very similar to this problem's matrix, but on a much larger and intricate scale