1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to check if a
number is palindrome or not*/
bool isPalindrome(int n) {
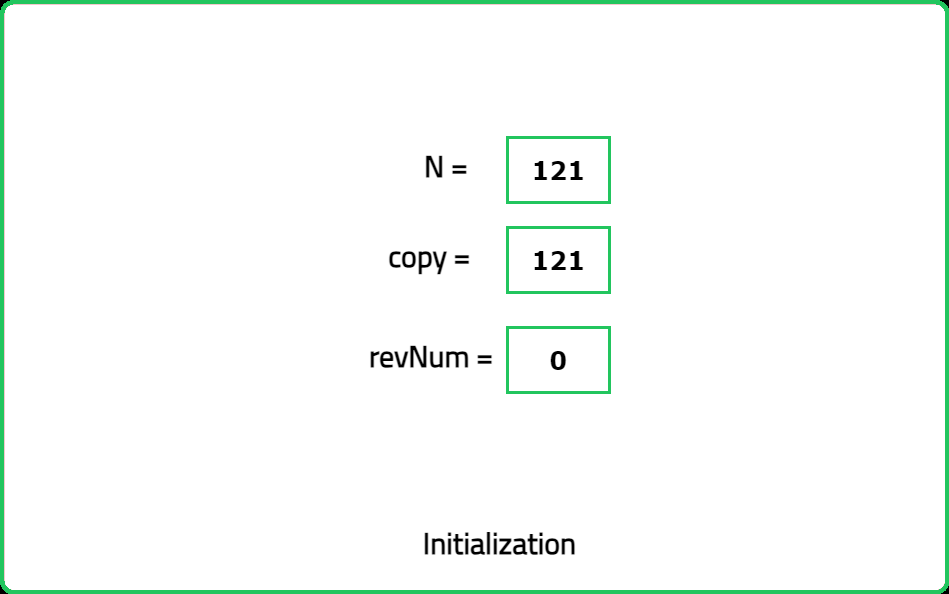
// Create a copy of original number
int copy = n;
/* After the code, revNum will
contain the reversed number */
int revNum = 0;
/* Keep on iterating while there
are digits left to extract */
while(n > 0) {
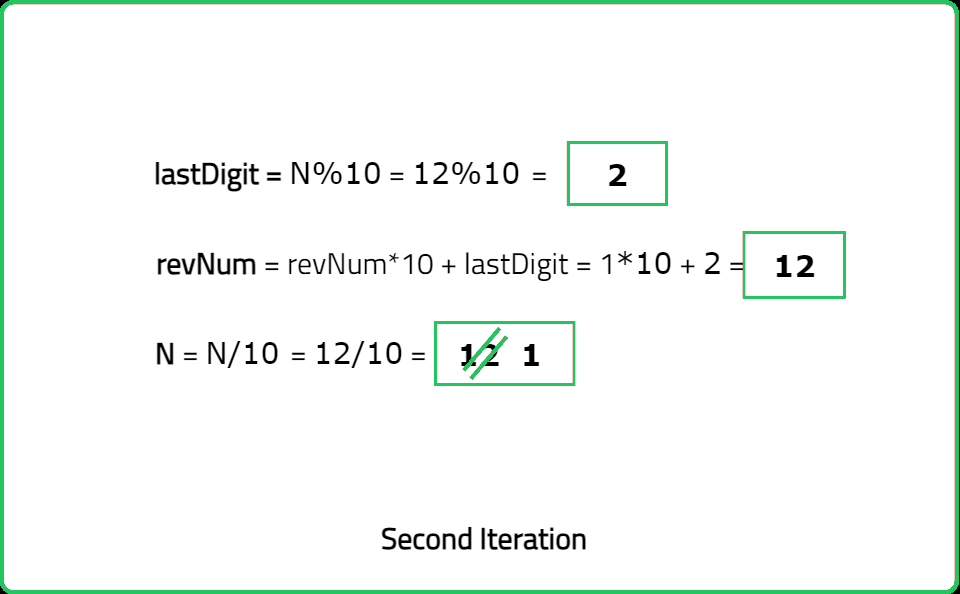
int lastDigit = n % 10;
/* Pushing last digit at the
back of reversed number */
revNum = (revNum * 10) + lastDigit;
n = n / 10;
}
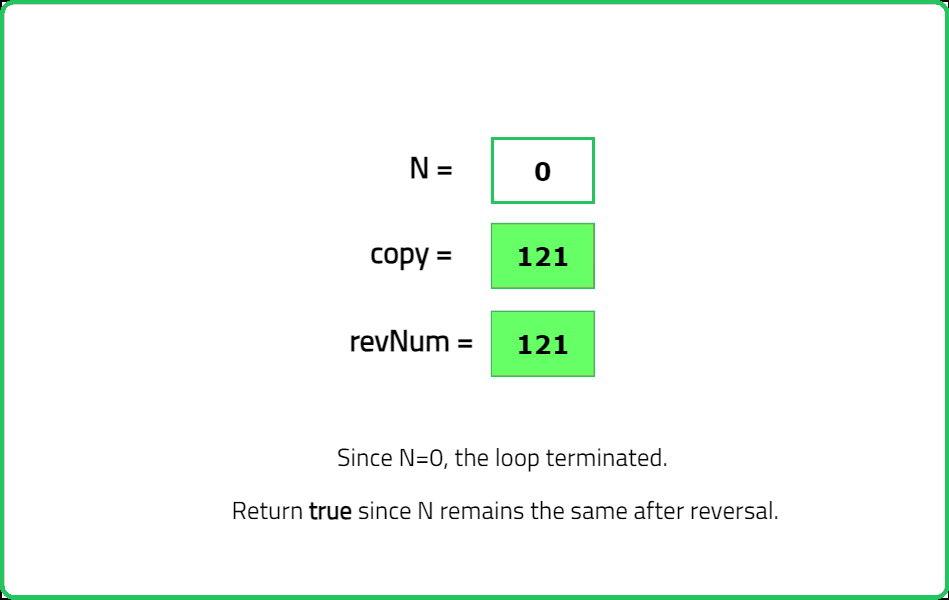
/* Return true if the reversed and
copy of original number is same */
if(revNum == copy) return true;
return false;
}
};
int main()
{
int n = 12321;
/* Creating and instance of
Solution class */
Solution sol;
// Function call to check if n is a palindrome
bool ans = sol.isPalindrome(n);
if(ans) cout << "The given number is a palindrome";
else cout << "The given number is not a palindrome";
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445
class Solution {
/* Function to check if a
number is palindrome or not */
public boolean isPalindrome(int n) {
// Create a copy of original number
int copy = n;
/* After the code, revNum will
contain the reversed number */
int revNum = 0;
/* Keep on iterating while there
are digits left to extract */
while (n > 0) {
int lastDigit = n % 10;
/* Pushing last digit at the
back of reversed number */
revNum = (revNum * 10) + lastDigit;
n = n / 10;
}
/* Return true if the reversed and
copy of original number is same */
return revNum == copy;
}
public static void main(String[] args) {
int n = 12321;
/* Creating an instance of
Solution class */
Solution sol = new Solution();
// Function call to check if n is a palindrome
boolean ans = sol.isPalindrome(n);
if (ans) {
System.out.println("The given number is a palindrome");
} else {
System.out.println("The given number is not a palindrome");
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839
class Solution:
# Function to check if a
# number is palindrome or not
def isPalindrome(self, n):
# Create a copy of original number
copy = n
# After the code, revNum will
# contain the reversed number
revNum = 0
# Keep on iterating while there
# are digits left to extract
while n > 0:
lastDigit = n % 10
# Pushing last digit at the
# back of reversed number
revNum = (revNum * 10) + lastDigit
n = n // 10
# Return true if the reversed and
# copy of original number is same
return revNum == copy
# Input number
n = 12321
# Creating an instance of Solution class
sol = Solution()
# Function call to check if n is a palindrome
ans = sol.isPalindrome(n)
if ans:
print("The given number is a palindrome")
else:
print("The given number is not a palindrome")
1234567891011121314151617181920212223242526272829303132333435363738394041424344
class Solution {
/* Function to check if a
number is palindrome or not */
isPalindrome(n) {
// Create a copy of original number
let copy = n;
/* After the code, revNum will
contain the reversed number */
let revNum = 0;
/* Keep on iterating while there
are digits left to extract */
while (n > 0) {
let lastDigit = n % 10;
/* Pushing last digit at the
back of reversed number */
revNum = (revNum * 10) + lastDigit;
n = Math.floor(n / 10);
}
/* Return true if the reversed and
copy of original number is same */
return revNum === copy;
}
}
// Input number
let n = 12321;
/* Creating an instance of
Solution class */
let sol = new Solution();
// Function call to check if n is a palindrome
let ans = sol.isPalindrome(n);
if (ans) {
console.log("The given number is a palindrome");
} else {
console.log("The given number is not a palindrome");
}