123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181
#include <bits/stdc++.h>
using namespace std;
class DisjointSet {
public:
/* To store the ranks, parents and
sizes of different set of vertices */
vector<int> rank, parent, size;
// Constructor
DisjointSet(int n) {
rank.resize(n + 1, 0);
parent.resize(n + 1);
size.resize(n + 1);
for (int i = 0; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// Function to find ultimate parent
int findUPar(int node) {
if (node == parent[node])
return node;
return parent[node] = findUPar(parent[node]);
}
// Function to implement union by rank
void unionByRank(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (rank[ulp_u] < rank[ulp_v]) {
parent[ulp_u] = ulp_v;
}
else if (rank[ulp_v] < rank[ulp_u]) {
parent[ulp_v] = ulp_u;
}
else {
parent[ulp_v] = ulp_u;
rank[ulp_u]++;
}
}
// Function to implement union by size
void unionBySize(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (size[ulp_u] < size[ulp_v]) {
parent[ulp_u] = ulp_v;
size[ulp_v] += size[ulp_u];
}
else {
parent[ulp_v] = ulp_u;
size[ulp_u] += size[ulp_v];
}
}
};
// Solution class
class Solution{
private:
// DelRow and delCol for neighbors
vector<int> delRow = {-1, 0, 1, 0};
vector<int> delCol = {0, 1, 0, -1};
/* Helper Function to check if a
pixel is within boundaries */
bool isValid(int &i, int &j,
int &n, int &m) {
// Return false if pixel is invalid
if(i < 0 || i >= n) return false;
if(j < 0 || j >= m) return false;
// Return true if pixel is valid
return true;
}
public:
/* Function to return the nunmber
of islands after each operation */
vector<int> numOfIslands(int n, int m,
vector<vector<int>> &A) {
// Disjoint set Data structure
DisjointSet ds(n * m);
// Visited array
int vis[n][m];
memset(vis, 0, sizeof vis);
// To store the count of islands
int cnt = 0;
// To store the result
vector<int> ans;
// Perform each operation
for (auto it : A) {
int row = it[0]; // Row
int col = it[1]; // Column
/* If already a land cell, no new
islands will be formed */
if (vis[row][col] == 1) {
ans.push_back(cnt);
continue;
}
// Make the cell as land
vis[row][col] = 1;
/* Increment the count considering
the land cell was alone */
cnt++;
// Check all the neighbors
for (int ind = 0; ind < 4; ind++) {
// Get the coordinates of cell
int newRow = row + delRow[ind];
int newCol = col + delCol[ind];
// If the cell is a valid land cell
if (isValid(newRow, newCol, n, m) &&
vis[newRow][newCol] == 1) {
// Get the node and adjacent node number
int nodeNo = row * m + col;
int adjNodeNo = newRow * m + newCol;
// If not already conencted, perfom the union
if (ds.findUPar(nodeNo) !=
ds.findUPar(adjNodeNo)) {
// Decrement count
cnt--;
// Perform the union
ds.unionBySize(nodeNo, adjNodeNo);
}
}
}
/* Store the number of islands after
current operation in the result list */
ans.push_back(cnt);
}
// Return the result
return ans;
}
};
int main() {
int n = 4, m = 5, k = 4;
vector<vector<int>> A = {
{1,1},
{0,1},
{3,3},
{3,4}
};
// Creating instance of Solution class
Solution sol;
/* Function call to return the number
of islands after each operation */
vector<int> ans = sol.numOfIslands(n, m, A);
// Output
cout << "The number of islands after each operations are: ";
for(int i=0; i < ans.size(); i++) {
cout << ans[i] << " ";
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170
import java.util.*;
class DisjointSet {
/* To store the ranks, parents and
sizes of different set of vertices */
int[] rank, parent, size;
// Constructor
DisjointSet(int n) {
rank = new int[n + 1];
parent = new int[n + 1];
size = new int[n + 1];
for (int i = 0; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// Function to find ultimate parent
int findUPar(int node) {
if (node == parent[node])
return node;
return parent[node] = findUPar(parent[node]);
}
// Function to implement union by rank
void unionByRank(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (rank[ulp_u] < rank[ulp_v]) {
parent[ulp_u] = ulp_v;
}
else if (rank[ulp_v] < rank[ulp_u]) {
parent[ulp_v] = ulp_u;
}
else {
parent[ulp_v] = ulp_u;
rank[ulp_u]++;
}
}
// Function to implement union by size
void unionBySize(int u, int v) {
int ulp_u = findUPar(u);
int ulp_v = findUPar(v);
if (ulp_u == ulp_v) return;
if (size[ulp_u] < size[ulp_v]) {
parent[ulp_u] = ulp_v;
size[ulp_v] += size[ulp_u];
}
else {
parent[ulp_v] = ulp_u;
size[ulp_u] += size[ulp_v];
}
}
}
// Solution class
class Solution {
// DelRow and delCol for neighbors
int[] delRow = {-1, 0, 1, 0};
int[] delCol = {0, 1, 0, -1};
/* Helper Function to check if a
cell is within boundaries */
boolean isValid(int i, int j, int n, int m) {
// Return false if cell is invalid
if (i < 0 || i >= n) return false;
if (j < 0 || j >= m) return false;
// Return true if cell is valid
return true;
}
/* Function to return the number
of islands after each operation */
public List<Integer> numOfIslands(int n, int m, int[][] A) {
// Disjoint set Data structure
DisjointSet ds = new DisjointSet(n * m);
// Visited array
int[][] vis = new int[n][m];
for (int[] row : vis) Arrays.fill(row, 0);
// To store the count of islands
int cnt = 0;
// To store the result
List<Integer> ans = new ArrayList<>();
// Perform each operation
for (int[] it : A) {
int row = it[0]; // Row
int col = it[1]; // Column
/* If already a land cell, no new
islands will be formed */
if (vis[row][col] == 1) {
ans.add(cnt);
continue;
}
// Make the cell as land
vis[row][col] = 1;
/* Increment the count considering
the land cell was alone */
cnt++;
// Check all the neighbors
for (int ind = 0; ind < 4; ind++) {
// Get the coordinates of cell
int newRow = row + delRow[ind];
int newCol = col + delCol[ind];
// If the cell is a valid land cell
if (isValid(newRow, newCol, n, m) &&
vis[newRow][newCol] == 1) {
// Get the node and adjacent node number
int nodeNo = row * m + col;
int adjNodeNo = newRow * m + newCol;
// If not already connected, perform the union
if (ds.findUPar(nodeNo) !=
ds.findUPar(adjNodeNo)) {
// Decrement count
cnt--;
// Perform the union
ds.unionBySize(nodeNo, adjNodeNo);
}
}
}
/* Store the number of islands after
current operation in the result list */
ans.add(cnt);
}
// Return the result
return ans;
}
public static void main(String[] args) {
int n = 4, m = 5, k = 4;
int[][] A = {
{1, 1},
{0, 1},
{3, 3},
{3, 4}
};
// Creating instance of Solution class
Solution sol = new Solution();
/* Function call to return the number of islands after each operation */
List<Integer> ans = sol.numOfIslands(n, m, A);
// Output
System.out.print("The number of islands after each operations are: ");
for (int num : ans) {
System.out.print(num + " ");
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146
class DisjointSet:
# To store the ranks, parents and sizes
# of different set of vertices
def __init__(self, n):
self.rank = [0] * (n + 1)
self.parent = list(range(n + 1))
self.size = [1] * (n + 1)
# Function to find ultimate parent
def findUPar(self, node):
if node == self.parent[node]:
return node
self.parent[node] = self.findUPar(self.parent[node])
return self.parent[node]
# Function to implement union by rank
def unionByRank(self, u, v):
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
if ulp_u == ulp_v:
return
if self.rank[ulp_u] < self.rank[ulp_v]:
self.parent[ulp_u] = ulp_v
elif self.rank[ulp_v] < self.rank[ulp_u]:
self.parent[ulp_v] = ulp_u
else:
self.parent[ulp_v] = ulp_u
self.rank[ulp_u] += 1
# Function to implement union by size
def unionBySize(self, u, v):
ulp_u = self.findUPar(u)
ulp_v = self.findUPar(v)
if ulp_u == ulp_v:
return
if self.size[ulp_u] < self.size[ulp_v]:
self.parent[ulp_u] = ulp_v
self.size[ulp_v] += self.size[ulp_u]
else:
self.parent[ulp_v] = ulp_u
self.size[ulp_u] += self.size[ulp_v]
# Solution class
class Solution:
# DelRow and delCol for neighbors
delRow = [-1, 0, 1, 0]
delCol = [0, 1, 0, -1]
# Helper Function to check if a
# pixel is within boundaries
def isValid(self, i, j, n, m):
# Return false if pixel is invalid
if i < 0 or i >= n:
return False
if j < 0 or j >= m:
return False
# Return true if pixel is valid
return True
# Function to return the number of
# islands after each operation
def numOfIslands(self, n, m, A):
# Disjoint set Data structure
ds = DisjointSet(n * m)
# Visited array
vis = [[0] * m for _ in range(n)]
# To store the count of islands
cnt = 0
# To store the result
ans = []
# Perform each operation
for it in A:
row = it[0] # Row
col = it[1] # Column
# If already a land cell, no new
# islands will be formed
if vis[row][col] == 1:
ans.append(cnt)
continue
# Make the cell as land
vis[row][col] = 1
# Increment the count considering
# the land cell was alone
cnt += 1
# Check all the neighbors
for ind in range(4):
# Get the coordinates of cell
newRow = row + self.delRow[ind]
newCol = col + self.delCol[ind]
# If the cell is a valid land cell
if (self.isValid(newRow, newCol, n, m) and
vis[newRow][newCol] == 1):
# Get the node and adjacent node number
nodeNo = row * m + col
adjNodeNo = newRow * m + newCol
# If not already connected, perform the union
if ds.findUPar(nodeNo) != ds.findUPar(adjNodeNo):
# Decrement count
cnt -= 1
# Perform the union
ds.unionBySize(nodeNo, adjNodeNo)
# Store the number of islands after
# current operation in the result list
ans.append(cnt)
# Return the result
return ans
# Main function
if __name__ == "__main__":
n = 4
m = 5
k = 4
A = [
[1, 1],
[0, 1],
[3, 3],
[3, 4]
]
# Creating instance of Solution class
sol = Solution()
# Function call to return the number of
# islands after each operation
ans = sol.numOfIslands(n, m, A)
# Output
print("The number of islands after each operations are: ", end="")
for num in ans:
print(num, end=" ")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160
class DisjointSet {
/* To store the ranks, parents and
sizes of different set of vertices */
constructor(n) {
this.rank = new Array(n + 1).fill(0);
this.parent = new Array(n + 1).fill(0).map((_, i) => i);
this.size = new Array(n + 1).fill(1);
}
// Function to find ultimate parent
findUPar(node) {
if (node === this.parent[node])
return node;
this.parent[node] = this.findUPar(this.parent[node]);
return this.parent[node];
}
// Function to implement union by rank
unionByRank(u, v) {
const ulp_u = this.findUPar(u);
const ulp_v = this.findUPar(v);
if (ulp_u === ulp_v) return;
if (this.rank[ulp_u] < this.rank[ulp_v]) {
this.parent[ulp_u] = ulp_v;
} else if (this.rank[ulp_v] < this.rank[ulp_u]) {
this.parent[ulp_v] = ulp_u;
} else {
this.parent[ulp_v] = ulp_u;
this.rank[ulp_u]++;
}
}
// Function to implement union by size
unionBySize(u, v) {
const ulp_u = this.findUPar(u);
const ulp_v = this.findUPar(v);
if (ulp_u === ulp_v) return;
if (this.size[ulp_u] < this.size[ulp_v]) {
this.parent[ulp_u] = ulp_v;
this.size[ulp_v] += this.size[ulp_u];
} else {
this.parent[ulp_v] = ulp_u;
this.size[ulp_u] += this.size[ulp_v];
}
}
}
// Solution class
class Solution {
constructor() {
// DelRow and delCol for neighbors
this.delRow = [-1, 0, 1, 0];
this.delCol = [0, 1, 0, -1];
}
// Helper Function to check if a pixel is within boundaries
isValid(i, j, n, m) {
// Return false if pixel is invalid
if (i < 0 || i >= n) return false;
if (j < 0 || j >= m) return false;
// Return true if pixel is valid
return true;
}
/* Function to return the number of
islands after each operation */
numOfIslands(n, m, A) {
// Disjoint set Data structure
const ds = new DisjointSet(n * m);
// Visited array
const vis = Array.from(
{ length: n }, () => Array(m).fill(0)
);
// To store the count of islands
let cnt = 0;
// To store the result
const ans = [];
// Perform each operation
for (const it of A) {
const row = it[0]; // Row
const col = it[1]; // Column
/* If already a land cell, no
new islands will be formed */
if (vis[row][col] === 1) {
ans.push(cnt);
continue;
}
// Make the cell as land
vis[row][col] = 1;
/* Increment the count considering
the land cell was alone */
cnt++;
// Check all the neighbors
for (let ind = 0; ind < 4; ind++) {
// Get the coordinates of cell
const newRow = row + this.delRow[ind];
const newCol = col + this.delCol[ind];
// If the cell is a valid land cell
if (this.isValid(newRow, newCol, n, m) &&
vis[newRow][newCol] === 1) {
// Get the node and adjacent node number
const nodeNo = row * m + col;
const adjNodeNo = newRow * m + newCol;
// If not already connected, perform the union
if (ds.findUPar(nodeNo) !== ds.findUPar(adjNodeNo)) {
// Decrement count
cnt--;
// Perform the union
ds.unionBySize(nodeNo, adjNodeNo);
}
}
}
/* Store the number of islands after current
operation in the result list */
ans.push(cnt);
}
// Return the result
return ans;
}
}
// Main function
const main = () => {
const n = 4;
const m = 5;
const k = 4;
const A = [
[1, 1],
[0, 1],
[3, 3],
[3, 4]
];
// Creating instance of Solution class
const sol = new Solution();
/* Function call to return the number of
islands after each operation */
const ans = sol.numOfIslands(n, m, A);
// Output
console.log("The number of islands after each operations are: ", ans.join(" "));
}
main();
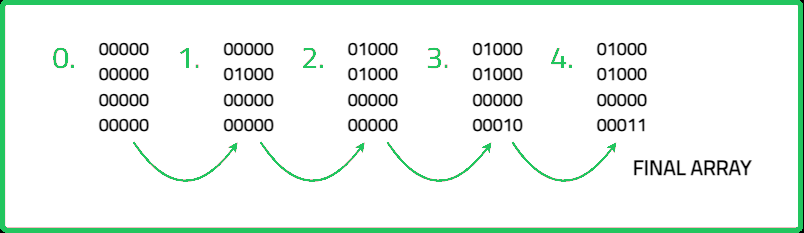
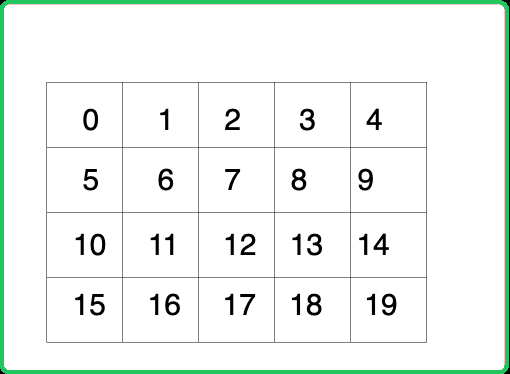 Thus, a number can be assigned to a cell having coordinates (i, j) in the following way:
Thus, a number can be assigned to a cell having coordinates (i, j) in the following way: 


