Sum of digits in a given number

Beginner Problems Basic Recursion Easy

This type of programming problem underlies many applications which need numeric validation, data integrity checks or compression tasks
For example, control digit computation, often used for credit cards number or ISBN code validation, implements similar logic
This problem's concept is also useful in checksum algorithms in data transmission to ensure data completeness
Also, digital root calculation, which is the essence of this task, is a part of various cryptographic techniques and pseudorandom number generation systems, fundamental for security and gaming software respectively

Given an integer num, repeatedly add all its digits until the result has only one digit, and return it.

Examples:

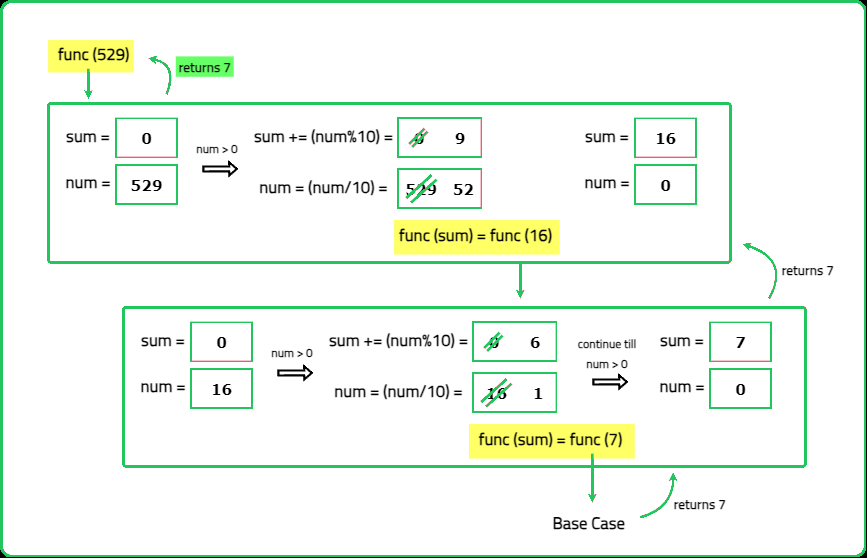
Input : num = 529

Output : 7

Explanation : In first iteration the digits sum will be = 5 + 2 + 9 => 16

In second iteration the digits sum will be 1 + 6 => 7.

Now single digit is remaining , so we return it.

Input : num = 101

Output : 2

Explanation : In first iteration the digits sum will be = 1 + 0 + 1 => 2

Now single digit is remaining , so we return it.

Input : num = 38

Constraints

0 <= num <= 2³¹ - 1

Company Tags

TCS Cognizant Accenture Infosys Capgemini Wipro IBM HCL Tech Mahindra MindTree

Editorial

Intution

To solve the problem of finding the sum of digits in a given number using recursion, the approach revolves around breaking down the problem into smaller, manageable parts. The key idea is to isolate the last digit of the number and add it to the result of a recursive call with the remaining digits. This process continues until the number reduces to a single digit. At each step, the last digit can be obtained using the modulus operation, and the rest of the number can be obtained using integer division. This recursive approach ensures that each digit is processed individually and accumulated to form the final sum.

Approach

Base Case: If the number is 0, return 0 as there are no more digits to process.
Recursive Case:
- Compute the last digit of the number using number % 10.
- Compute the remaining number by performing integer division number / 10.
- Make a recursive call with the remaining number and add the last digit to the result of this call.

Dry Run

Solution

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Method to compute the digital root of a number
    int addDigits(int num) {
        // Base case: if the number is a single digit, return it
        if (num < 10) {
            return num;
        }
        
        // Recursive case: sum the digits and continue
        int sum = 0;
        while (num > 0) {
            sum += num % 10;
            num /= 10;
        }
        return addDigits(sum);
    }
};

int main() {
    Solution solution;
    
    // Example number
    int num = 529;
    
    // Call the addDigits method and print the result
    int result = solution.addDigits(num);
    std::cout << "Sum of digits: " << result << std::endl;  // Expected output: 7
    
    return 0;
}
class Solution {
    // Method to compute the digital root of a number
    public int addDigits(int num) {
        // Base case: if the number is a single digit, return it
        if (num < 10) {
            return num;
        }
        
        // Recursive case: sum the digits and continue
        int sum = 0;
        while (num > 0) {
            sum += num % 10;
            num /= 10;
        }
        return addDigits(sum);
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        
        // Example number
        int num = 529;
        
        // Call the addDigits method and print the result
        int result = solution.addDigits(num);
        System.out.println("Sum of digits: " + result);  // Expected output: 7
    }
}
class Solution:
    def addDigits(self, num):
        # Base case: if the number is a single digit, return it
        if num < 10:
            return num
        
        # Recursive case: sum the digits and continue
        return self.addDigits(sum(int(digit) for digit in str(num)))

# Example usage
solution = Solution()

# Example number
num = 529

# Call the addDigits method and print the result
result = solution.addDigits(num)
print("Sum of digits:", result)  # Expected output: 7
class Solution {
    // Method to compute the digital root of a number
    addDigits(num) {
        // Base case: if the number is a single digit, return it
        if (num < 10) {
            return num;
        }
        
        // Recursive case: sum the digits and continue
        let sum = 0;
        while (num > 0) {
            sum += num % 10;
            num = Math.floor(num / 10);
        }
        return this.addDigits(sum);
    }
}

// Example usage
const solution = new Solution();

// Example number
const num = 529;

// Call the addDigits method and print the result
const result = solution.addDigits(num);
console.log("Sum of digits:", result);  // Expected output: 7

Complexity Analysis

Time Complexity O(log n) – This is because each recursive call processes a number with fewer digits than the previous call, leading to logarithmic time complexity in terms of the number of digits.

SpaceComplexity O(log n) – This space is required for the recursion stack, which grows with the number of digits in the number.

Code

Problem List