Single Number - I

Bit Manipulation Problems Medium Go Ad-Free - ₹20/mo

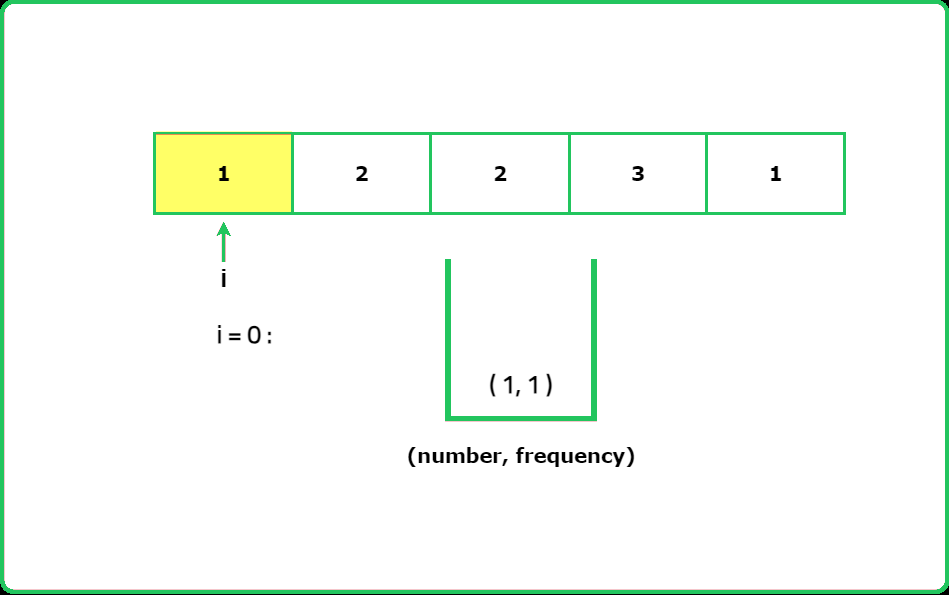
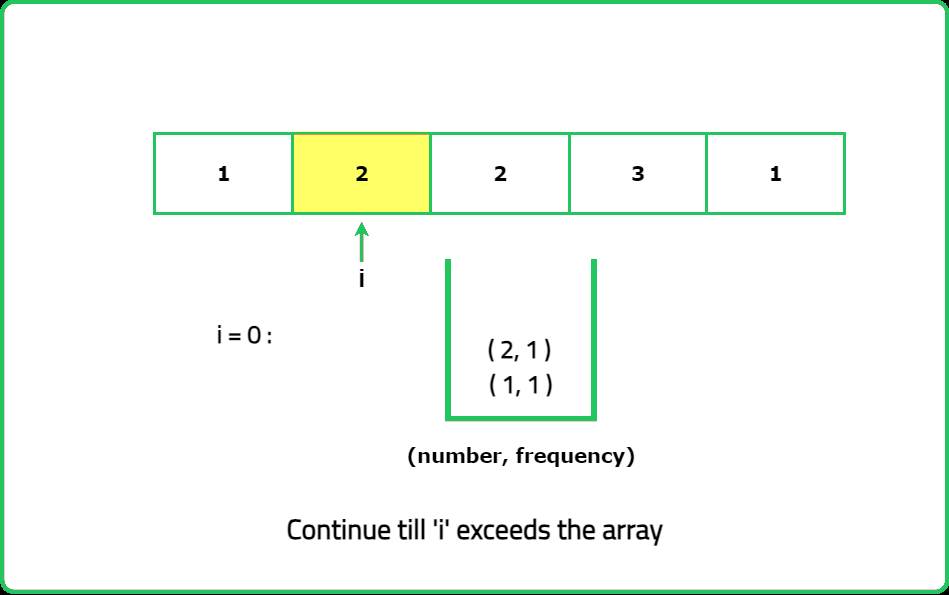
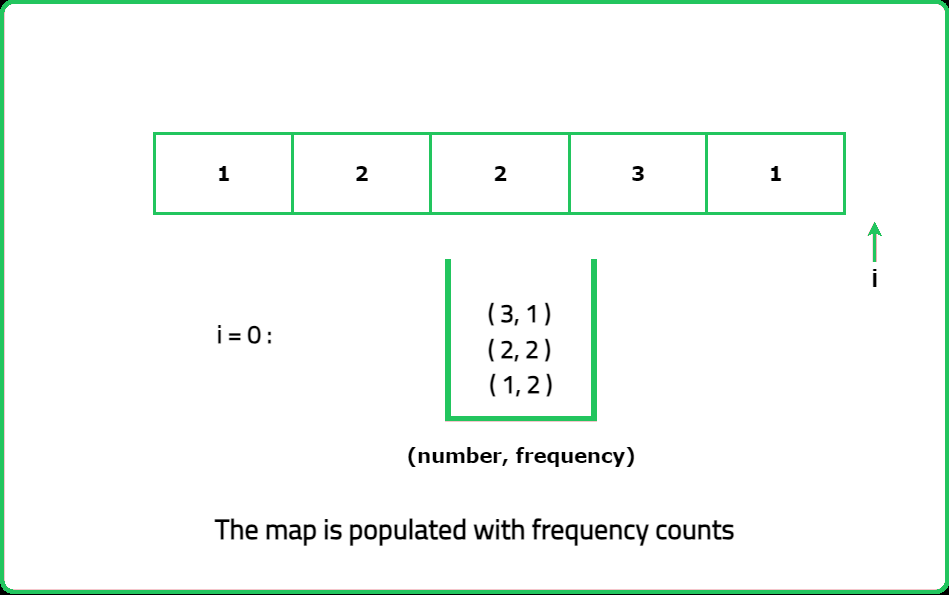
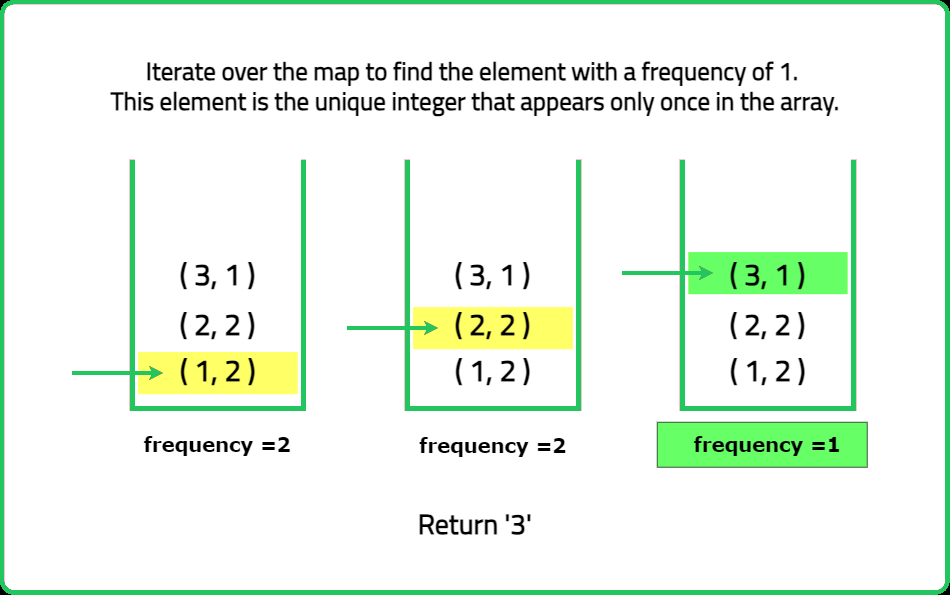
Given an array of nums of n integers. Every integer in the array appears twice except one integer. Find the number that appeared once in the array.

Examples:

Input : nums = [1, 2, 2, 4, 3, 1, 4]

Output : 3

Explanation : The integer 3 has appeared only once.

Input : nums = [5]

Output : 5

Explanation : The integer 5 has appeared only once.

Input : nums = [1, 3, 10, 3, 5, 1, 5]

Constraints

1 <= n <= 10⁵
-3*10⁵ <= nums[i] <= 3*10⁵

Hints

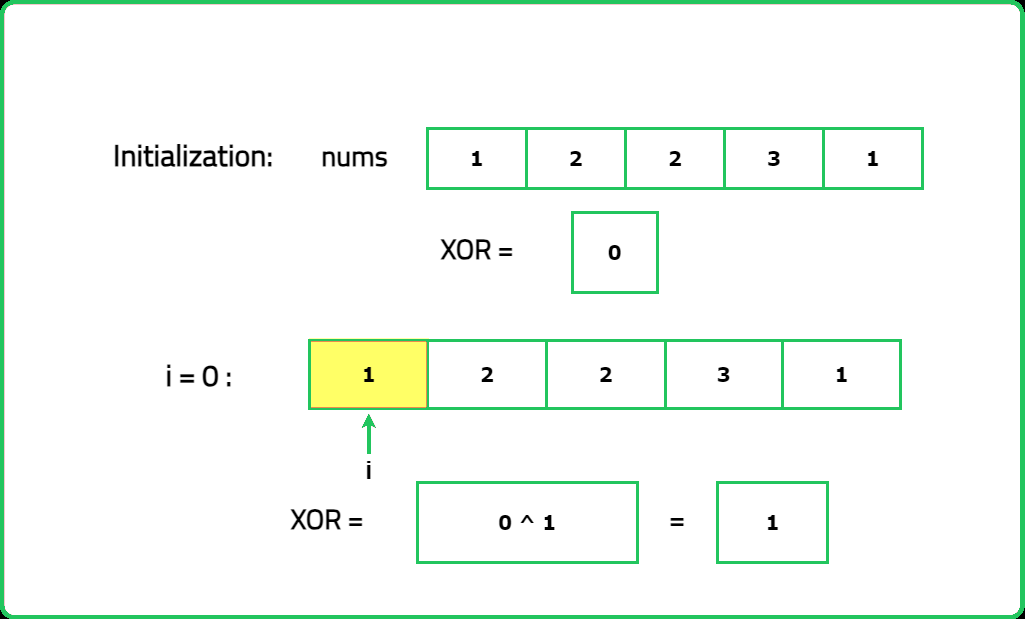
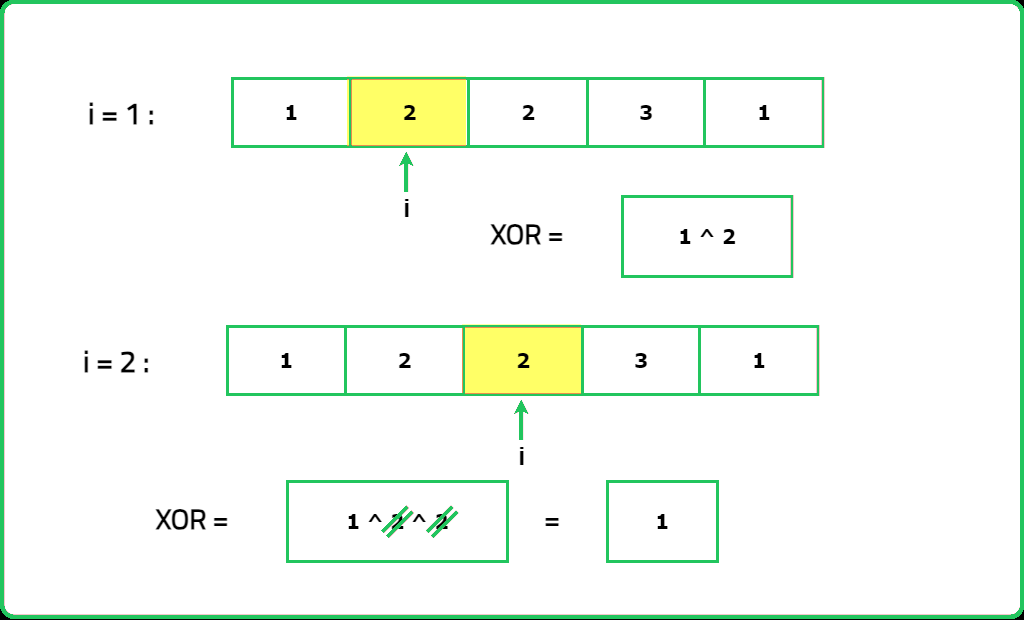
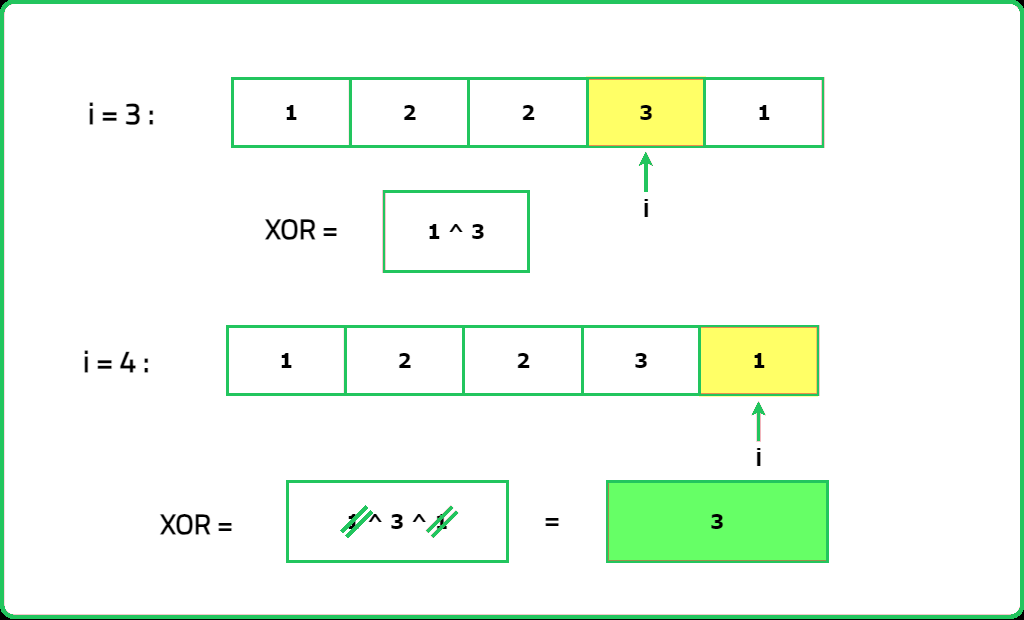
When you XOR all the numbers in the array, the duplicate numbers cancel out, leaving only the unique number.
Traverse the array and XOR all the elements together. At the end of the traversal, the result will be the number that appears only once because the XOR of duplicates will be zero.

Company Tags

Byju's Optum Roblox Instacart Wayfair Zoho Roche Philips Healthcare Teladoc Health HCL Technologies Visa Texas Instruments Activision Blizzard IBM Freshworks GE Healthcare OYO Rooms Intel Rakuten Cerner Twilio Zynga Cloudflare Docker JPMorgan Chase Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition:

The brute force way to solve this will be to utilize a frequency counting approach. By keeping track of the frequency of each element in the array, the element that appears only once can be easily identified.

Approach:

Use a hash map to store the frequency of each element in the array. The keys of the map are the elements of the array, and the values are their corresponding frequencies.
Traverse the entire array once, and for each element, update its frequency count in the map.
After populating the map with frequency counts, iterate over the map to find the element with a frequency of 1. This element is the unique integer that appears only once in the array.
Return the unique element found in the map. If no such element exists (though the problem guarantees that one does), return -1.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to get the single 
    number in the given array */
    int singleNumber(vector<int>& nums){
        
        /* Map to store the elements 
        and their frequencies */
        unordered_map <int, int> mpp;
        
        // Iterate on the array
        for(int i=0; i < nums.size(); i++) {
            mpp[nums[i]]++; //Update the map
        }
        
        //Iterate on the map
        for(auto it : mpp) {
            // If frequency is 1
            if(it.second == 1) {
                // Return the element
                return it.first;
            }
        }   
        
        /* Return -1, if there is no 
        number having frequency 1 */
        return -1;
    }
};

int main() {
    vector<int> nums = {1, 2, 2, 4, 3, 1, 4};
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to get the single 
    number in the given array */
    int ans = sol.singleNumber(nums);
    
    cout << "The single number in given array is: " << ans;
    
    return 0;
}
import java.util.HashMap;

class Solution {
    /* Function to get the single 
    number in the given array */
    public int singleNumber(int[] nums) {
        
        /* Map to store the elements 
        and their frequencies */
        HashMap<Integer, Integer> mpp = new HashMap<>();
        
        // Iterate on the array
        for (int num : nums) {
            mpp.put(num, mpp.getOrDefault(num, 0) + 1); //Update the map
        }
        
        //Iterate on the map
        for (int key : mpp.keySet()) {
            // If frequency is 1
            if (mpp.get(key) == 1) {
                // Return the element
                return key;
            }
        }   
        
        /* Return -1, if there is no 
        number having frequency 1 */
        return -1;
    }
    
    public static void main(String[] args) {
        int[] nums = {1, 2, 2, 4, 3, 1, 4};
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution(); 
        
        /* Function call to get the single 
        number in the given array */
        int ans = sol.singleNumber(nums);
        
        System.out.println("The single number in given array is: " + ans);
    }
}
class Solution:
    # Function to get the single 
    # number in the given array
    def singleNumber(self, nums):
        
        # Map to store the elements 
        # and their frequencies
        mpp = {}
        
        # Iterate on the array
        for num in nums:
            if num in mpp:
                mpp[num] += 1  #Update the map
            else:
                mpp[num] = 1  #Update the map
        
        # Iterate on the map
        for key, value in mpp.items():
            # If frequency is 1
            if value == 1:
                # Return the element
                return key
        
        # Return -1, if there is no 
        # number having frequency 1
        return -1

# Example usage
nums = [1, 2, 2, 4, 3, 1, 4]

# Creating an instance of 
# Solution class
sol = Solution() 

# Function call to get the single 
# number in the given array
ans = sol.singleNumber(nums)

print("The single number in given array is:", ans)
class Solution {
    /* Function to get the single 
    number in the given array */
    singleNumber(nums) {
        
        /* Map to store the elements 
        and their frequencies */
        let mpp = new Map();
        
        // Iterate on the array
        nums.forEach(num => {
            mpp.set(num, (mpp.get(num) || 0) + 1); //Update the map
        });
        
        // Iterate on the map
        for (let [key, value] of mpp) {
            // If frequency is 1
            if (value === 1) {
                // Return the element
                return key;
            }
        }   
        
        /* Return -1, if there is no 
        number having frequency 1 */
        return -1;
    }
}

// Example usage
let nums = [1, 2, 2, 4, 3, 1, 4];

/* Creating an instance of 
Solution class */
let sol = new Solution(); 

/* Function call to get the single 
number in the given array */
let ans = sol.singleNumber(nums);

console.log("The single number in given array is:", ans);

Complexity Analysis:

Time Complexity: O(N) (where N is the size of the array) –

Traversing the array to update the Hash Map - O(N).

Traversing on the map - O(N) (in worst case).

Space Complexity: O(N) – Using a hashmap data structure and in the worst-case (when all elements in the array are unique), it will store N key-value pairs.

Intuition:

The problem can be efficiently solved using the properties of the XOR bitwise operator. The key properties of XOR are:

a^a = 0 (XOR of any number with itself is 0).
a^0 = a (XOR of any number with 0 is the number itself).
XOR is both commutative and associative, meaning the order in which you apply XOR does not matter.

Using these properties, calculating XOR all the numbers in the array, the pairs of identical numbers will cancel each other out (because a ^ a = 0), and the result will be the number that appears only once.

Approach:

Start with a variable initialized to 0. This variable will be used to store the cumulative XOR of all numbers in the array.
Loop through each element in the array. For each element, update the cumulative XOR by applying the XOR operation between the current cumulative XOR value and the current array element.
After iterating through all the elements, the cumulative XOR will hold the value of the integer that appears only once in the array.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to get the single 
    number in the given array */
    int singleNumber(vector<int>& nums){
        /* Variable to store XOR
        of all numbers in array */
        int XOR = 0;
        
        /* Iterate on the array to
        find XOR of all elements */
        for(int i = 0; i < nums.size(); i++) {
            XOR ^= nums[i];    
        }
        
        // XOR stores the required answer
        return XOR;        
    }
};

int main() {
    vector<int> nums = {1, 2, 2, 4, 3, 1, 4};
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to get the single 
    number in the given array */
    int ans = sol.singleNumber(nums);
    
    cout << "The single number in given array is: " << ans;
    
    return 0;
}
import java.util.*;

class Solution {
    /* Function to get the single 
    number in the given array */
    public int singleNumber(int[] nums) {
        /* Variable to store XOR
        of all numbers in array */
        int XOR = 0;
        
        /* Iterate on the array to
        find XOR of all elements */
        for (int i = 0; i < nums.length; i++) {
            XOR ^= nums[i];    
        }
        
        // XOR stores the required answer
        return XOR;        
    }
}

public class Main {
    public static void main(String[] args) {
        int[] nums = {1, 2, 2, 4, 3, 1, 4};
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution(); 
        
        /* Function call to get the single 
        number in the given array */
        int ans = sol.singleNumber(nums);
        
        System.out.println("The single number in given array is: " + ans);
    }
}
class Solution:
    # Function to get the single 
    # number in the given array 
    def singleNumber(self, nums):
        # Variable to store XOR
        # of all numbers in array
        XOR = 0
        
        # Iterate on the array to
        # find XOR of all elements
        for num in nums:
            XOR ^= num
        
        # XOR stores the required answer
        return XOR

if __name__ == "__main__":
    nums = [1, 2, 2, 4, 3, 1, 4]
    
    # Creating an instance of 
    # Solution class 
    sol = Solution()
    
    # Function call to get the single 
    # number in the given array 
    ans = sol.singleNumber(nums)
    
    print(f"The single number in given array is: {ans}")
class Solution {
    /* Function to get the single 
    number in the given array */
    singleNumber(nums) {
        /* Variable to store XOR
        of all numbers in array */
        let XOR = 0;
        
        /* Iterate on the array to
        find XOR of all elements */
        for (let i = 0; i < nums.length; i++) {
            XOR ^= nums[i];    
        }
        
        // XOR stores the required answer
        return XOR;        
    }
}

const nums = [1, 2, 2, 4, 3, 1, 4];

/* Creating an instance of 
Solution class */
const sol = new Solution();

/* Function call to get the single 
number in the given array */
const ans = sol.singleNumber(nums);

console.log("The single number in given array is: " + ans);

Complexity Analysis:

Time Complexity: O(N) (where N is the size of array) – Traversing through the array once will result in O(N) TC.

Space Complexity: O(1) – Using constant space.

Frequently Occurring Doubts

Q: Can I solve this without using XOR?

A: Yes, you can use a hash map to count the frequency of each number and return the one with a count of 1. However, this approach uses O(n) time but also requires O(n) space.

Q: Why does XOR work for this problem?

A: XOR cancels out duplicate numbers because a⊕a=0. When all numbers in the array are XORed, only the unique number remains, as 0⊕unique number=unique number.

Interview Followup Questions

Q: How would you extend this problem if the unique number appears k times instead of 1?

A: XOR alone wouldn’t work. Instead, you could use bitwise counting to count the occurrences of each bit across all numbers and find the unique number that appears k times.

Q: How would you modify the solution if there were exactly two unique numbers?

A: XOR all elements to get a⊕b (the XOR of the two unique numbers). Then, isolate a differing bit and use it to partition the numbers into two groups, each containing one unique number.

Notes

Your notes are automatically saved in your browser's local storage and will persist across sessions on this device.

Problem Categories

Single Number - I

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code

Facts