Pre, Post, Inorder in one traversal
Binary Trees
Theory/Traversals
Easy
- In-order, pre-order and post-order are tree traversal methods that have real-life applications in the software industry
- For instance, in database systems, these traversal algorithms are often used to parse expression trees
- This is particularly important in optimizing queries or categorizing data
- Similarly, compilers make use of these algorithms for syntax checking, creating symbol tables, or generating machine code
- Fun fact, file system scans in operating systems are also modeled as a pre-order traversal of a tree!
Given a binary tree with root node. Return the In-order,Pre-order and Post-order traversal of the binary tree.
Examples:
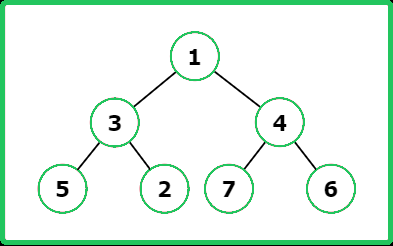
Input : root = [1, 3, 4, 5, 2, 7, 6 ]
Output : [ [5, 3, 2, 1, 7, 4, 6] , [1, 3, 5, 2, 4, 7, 6] , [5, 2, 3, 7, 6, 4, 1] ]
Explanation : The In-order traversal is [5, 3, 2, 1, 7, 4, 6].
The Pre-order traversal is [1, 3, 5, 2, 4, 7, 6].
The Post-order traversal is [5, 2, 3, 7, 6, 4, 1].
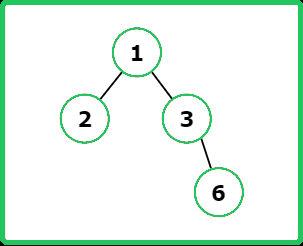
Input : root = [1, 2, 3, null, null, null, 6 ]
Output : [ [2, 1, 3, 6] , [1, 2, 3, 6] , [2, 6, 3, 1] ]
Explanation : The In-order traversal is [2, 1, 3, 6].
The Pre-order traversal is [1, 2, 3, 6].
The Post-order traversal is [2, 6, 3, 1].
Input : root = [5, 1, 2, 8, null, 4, 5, null, 6]
Constraints
- 1 <= Number of Nodes <= 105
- 0 <= Node.val <= 105
Hints
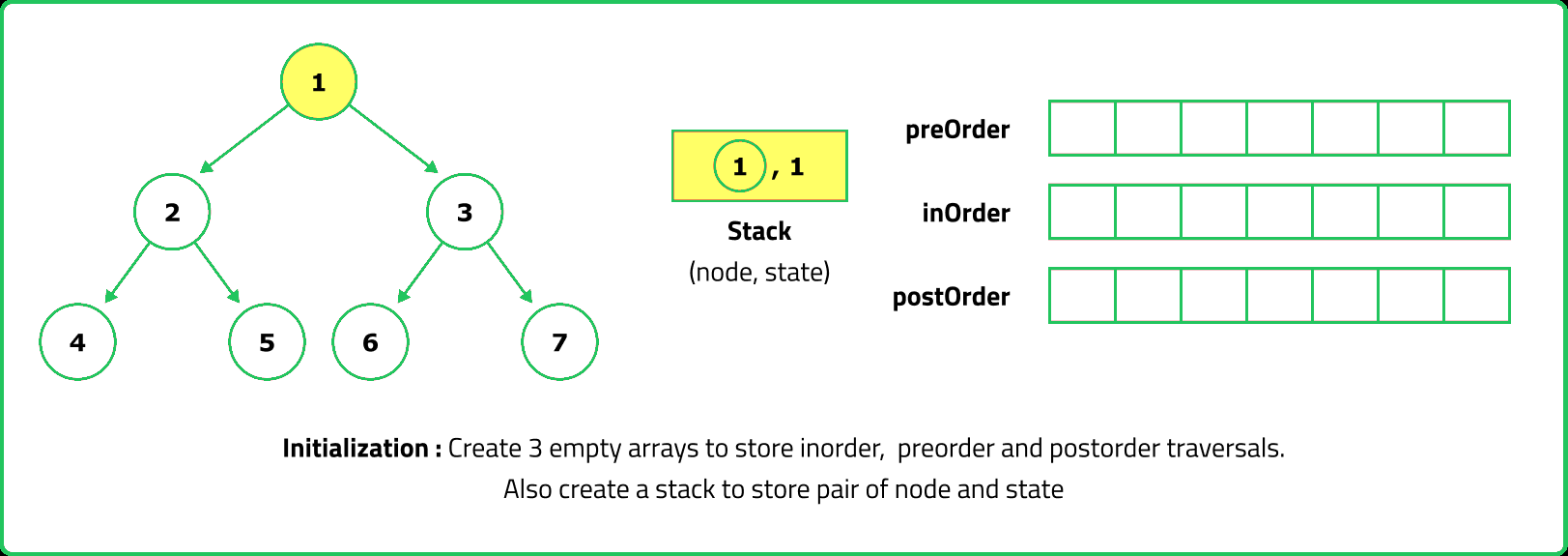
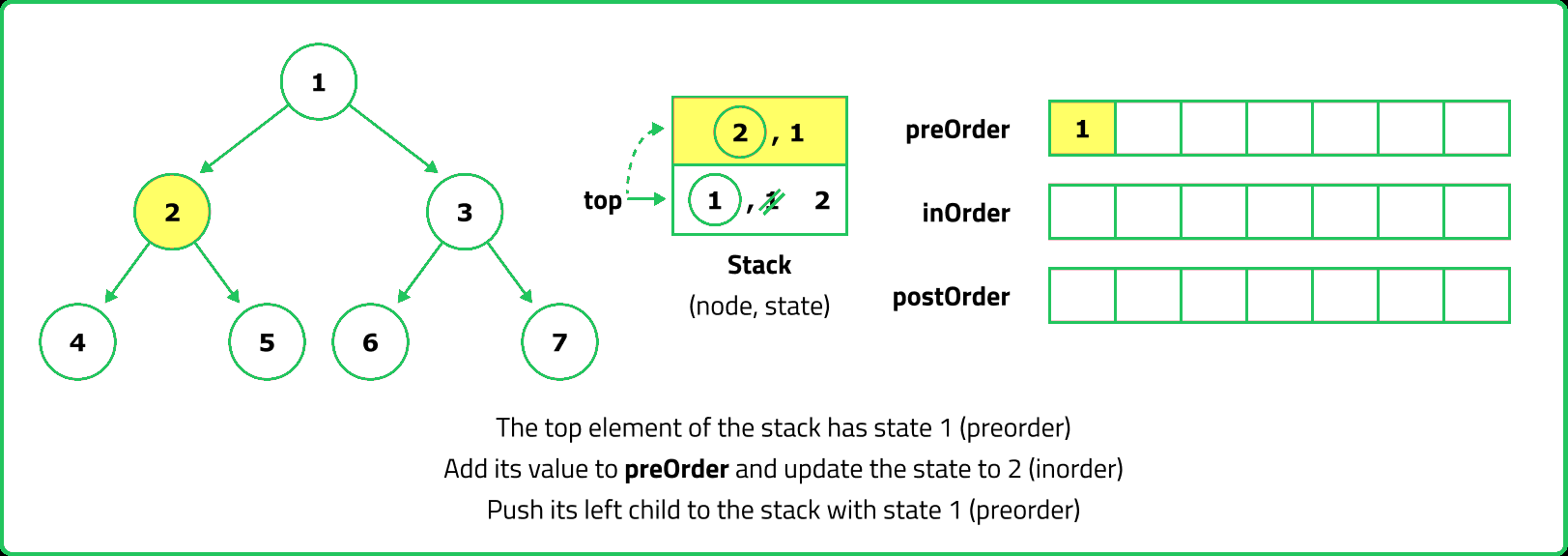
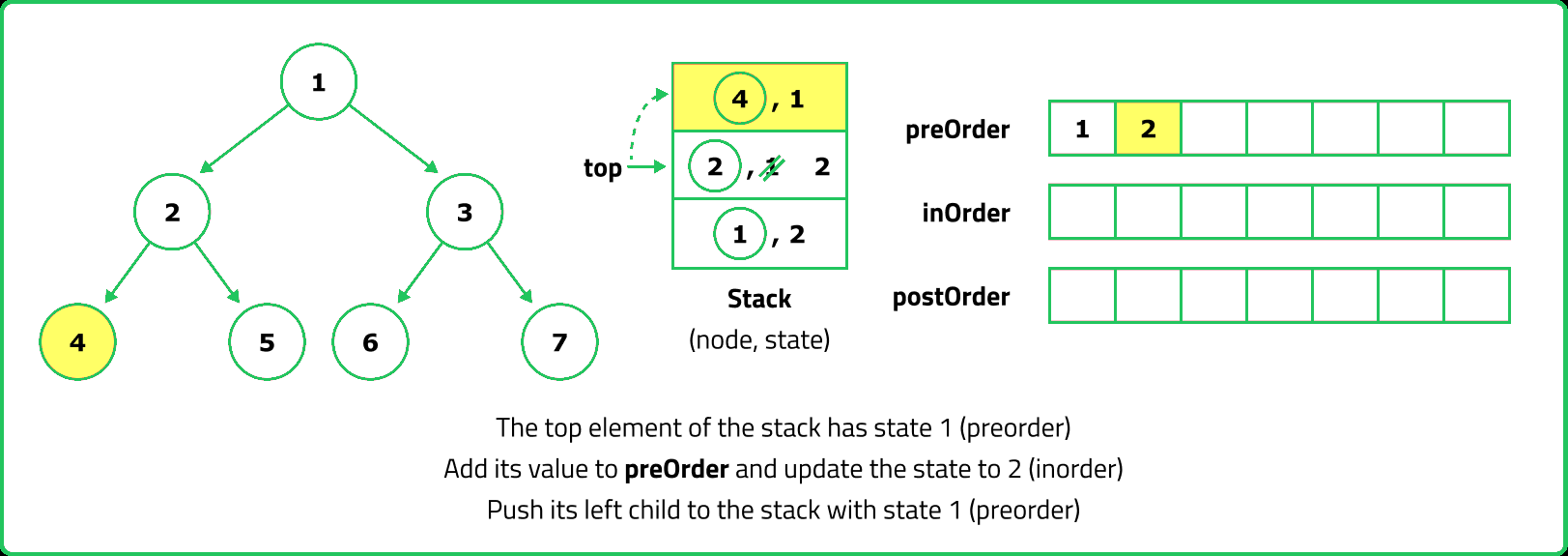
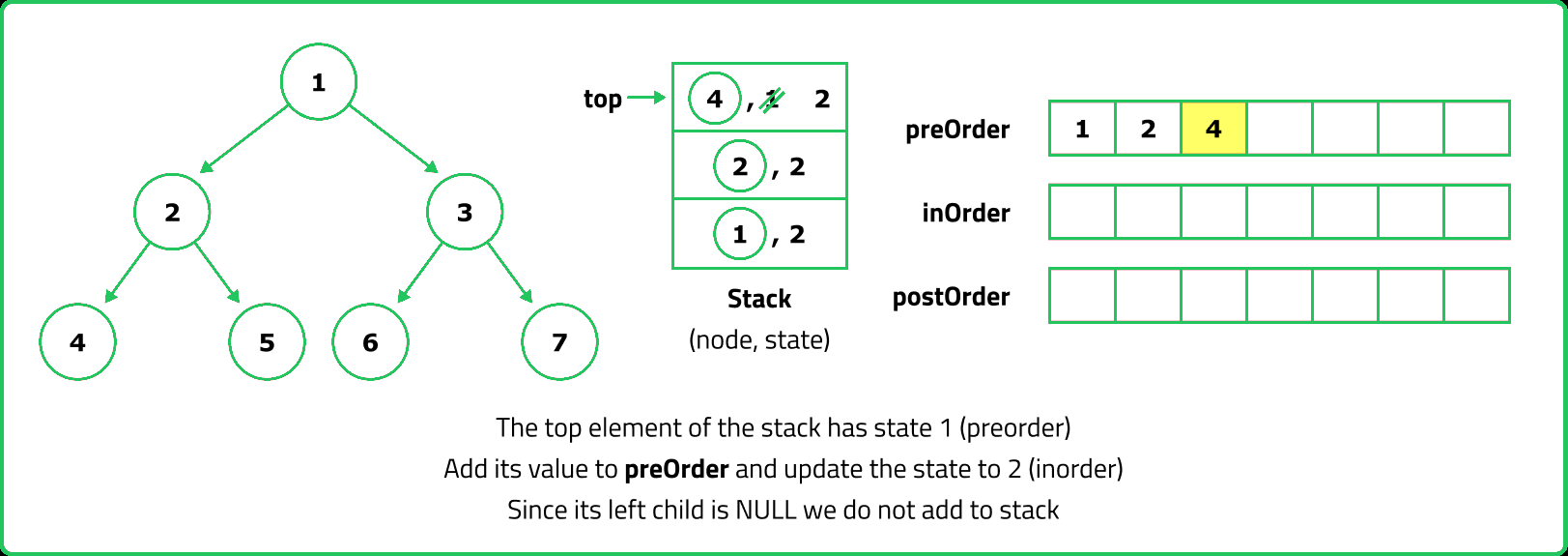
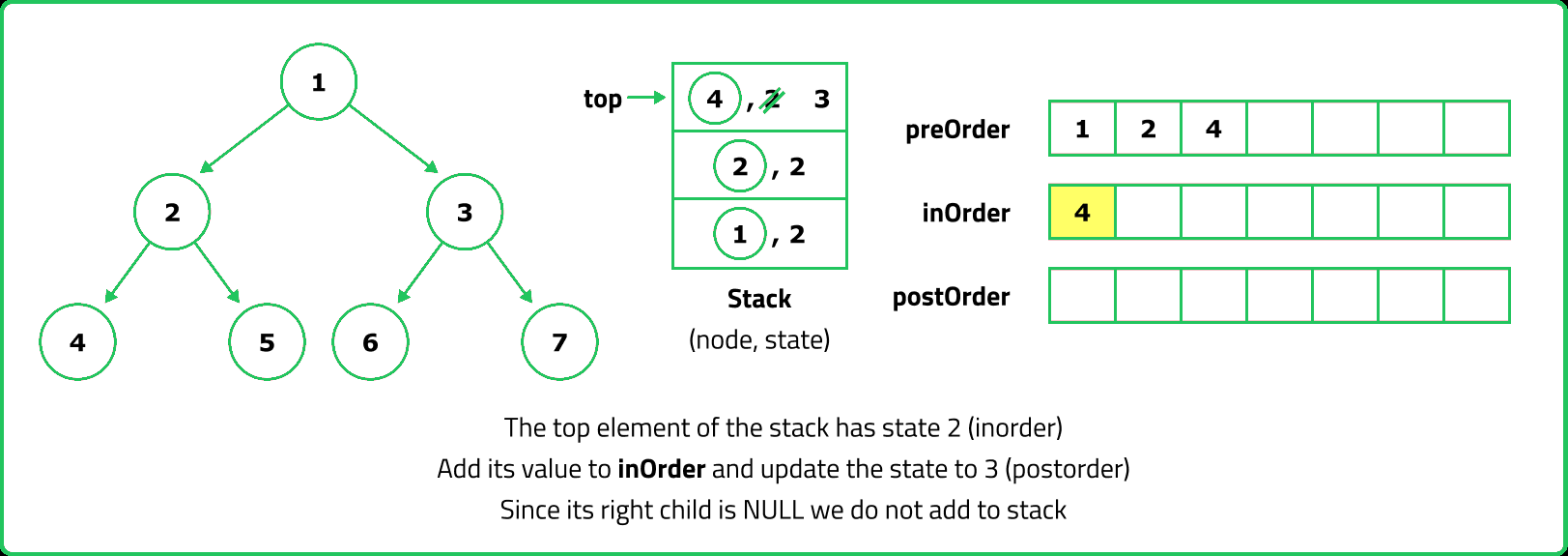
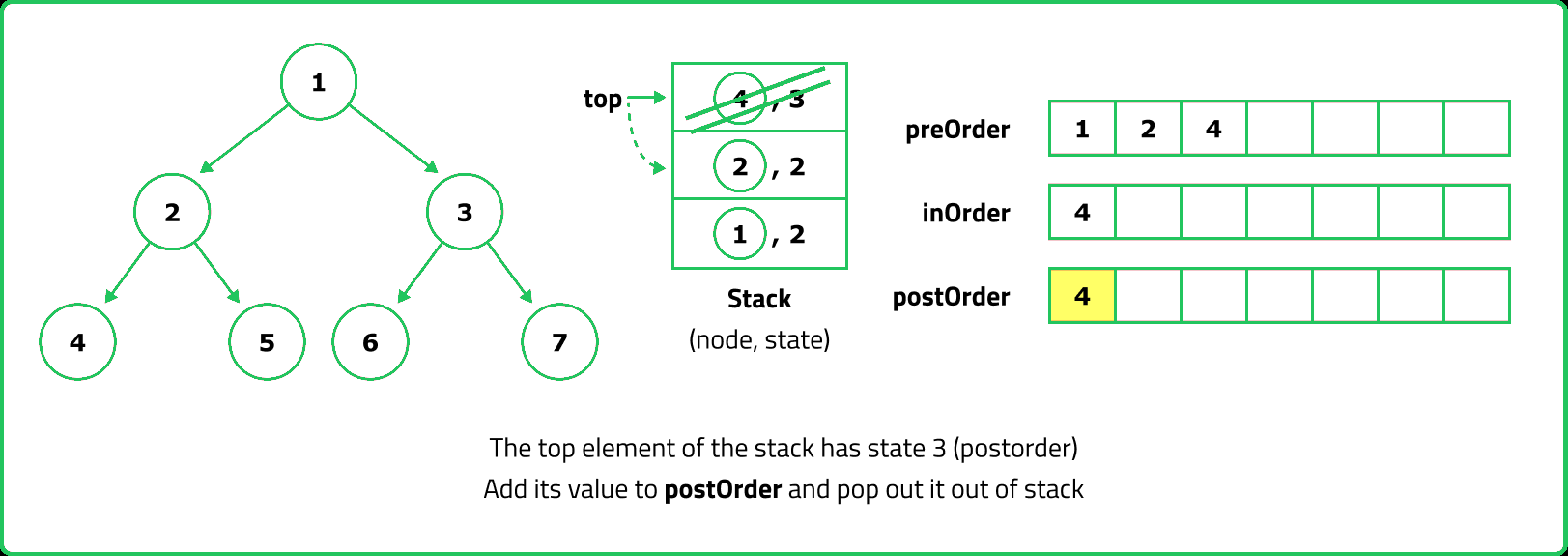
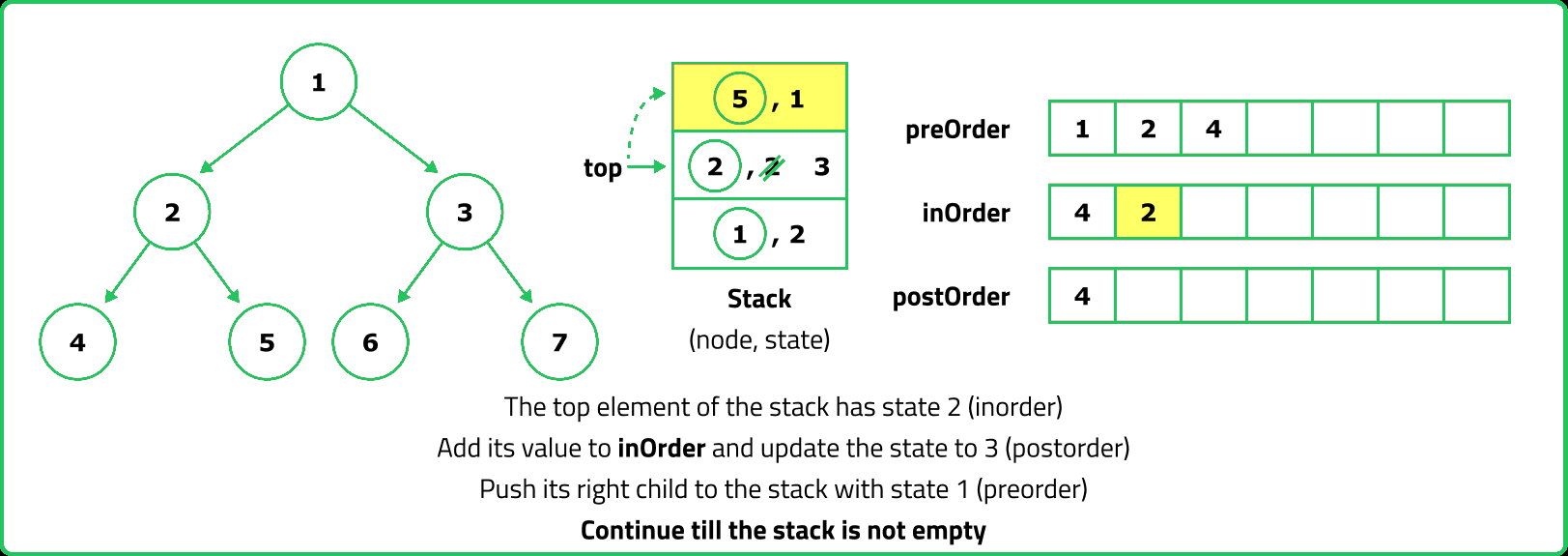
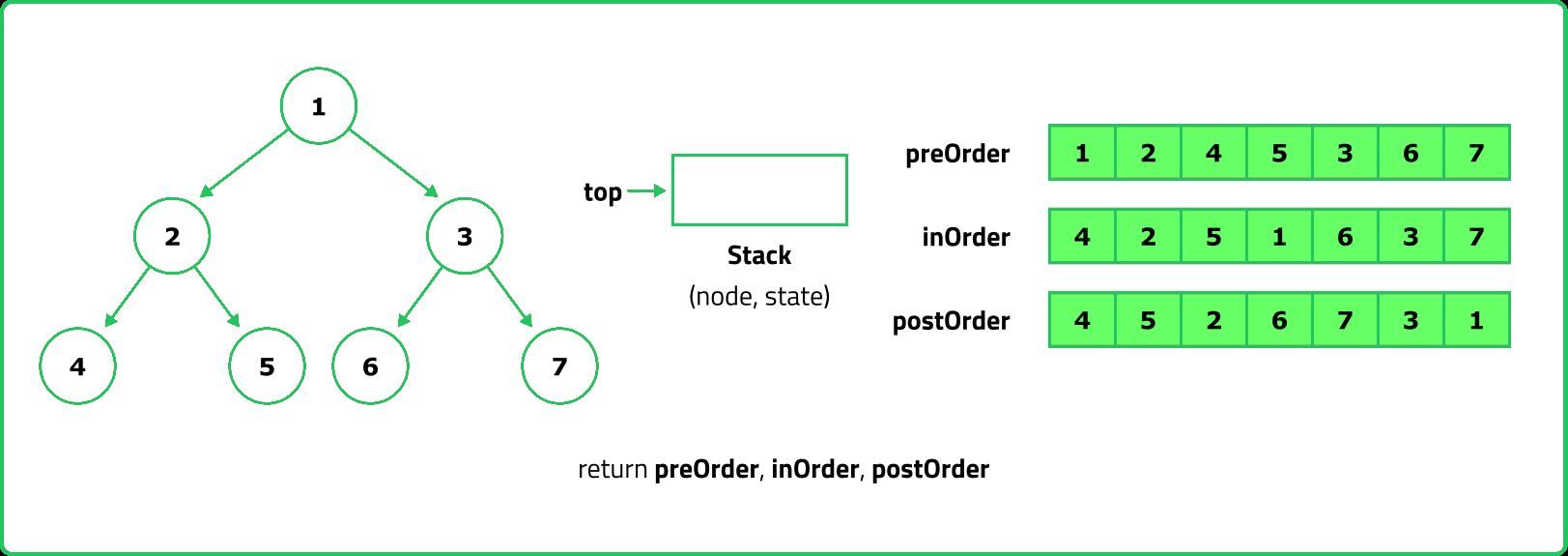
- For Preorder traversal, a stack is used to process nodes before pushing their children. Inorder traversal requires a stack to track nodes while traversing left, processing the root, and then moving right. Postorder traversal is trickier because the root must be visited last, which can be handled using two stacks or by modifying Preorder traversal.
Company Tags
Optum
Philips Healthcare
Activision Blizzard
Micron Technology
Riot Games
Cerner
Broadcom
Square
Nutanix
Siemens Healthineers
Docker
KPMG
HashiCorp
Red Hat
Robinhood
McKinsey & Company
Zoho
Qualcomm
Freshworks
Byju's
Texas Instruments
Unity Technologies
Epic Systems
Dropbox
Visa
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe