Minimise max distance to gas stations

Intuition:

The idea here is to use very straightforward approach to solve this problem by using extra space. Declare an array of size n-1, where n is the size of the array given. Each of its indexes will represent the respective sections between the given gas stations. In each iteration, identify the index, such that subtraction of element at that index from element at the very next index is the maximum. Then, insert new stations into that section to reduce that maximum distance. The number of stations inserted in each section will be tracked using the previously declared array of size n-1.

Finally, after placing all the stations find the maximum distance between two consecutive stations. Among all the values of distances, the maximum one will be our answer.

Approach:

First, declare an array ‘howMany’ of size n-1, to keep track of the number of placed gas stations, where n is the size of the array provided.
Next, traverse the gas stations from 1 to k using a loop and pick gas stations one at a time.
Then, using a nested loop, identify a index, such that subtraction of element at that index from element at the very next index is the maximum and insert the current gas station between arr[index] and arr[index+1] (i.e. howMany[i]++).
Finally, after placing all the new stations, find the distance between two consecutive gas stations. For a particular section, distance = section_length / (number_of_stations_ inserted+1) = (arr[i+1]-arr[i]) / (howMany[i]+1)
Among all the distances, the maximum one will be the answer.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to minimize the maximum
    distance between gas stations */
    double minimiseMaxDistance(vector<int>& arr, int k) {
        
        int n = arr.size(); 
        
        /* Array to store how many gas 
        stations are placed in each section*/
        vector<int> howMany(n - 1, 0); 

        // Place k gas stations
        for (int gasStations = 1; gasStations <= k; gasStations++) {
            double maxSection = -1;
            int maxInd = -1;

            /* Find the maximum section 
            and insert the gas station*/
            for (int i = 0; i < n - 1; i++) {
                double diff = arr[i + 1] - arr[i];
                double sectionLength = diff / (howMany[i] + 1);
                
                /* Update the maximum section
                length and its index */
                if (sectionLength > maxSection) {
                    maxSection = sectionLength;
                    maxInd = i;
                }
            }
            
            /* Insert the current gas 
            station into the section */
            howMany[maxInd]++;
        }

        // Find the maximum distance (answer)
        double maxAns = -1;
        for (int i = 0; i < n - 1; i++) {
            double diff = arr[i + 1] - arr[i];
            double sectionLength = diff / (howMany[i] + 1);
            maxAns = max(maxAns, sectionLength);
        }

        return maxAns;
    }
};

int main() {
    vector<int> arr = {1, 2, 3, 4, 5};
    int k = 4;

    // Create an instance of the Solution class
    Solution sol;

    // Call the minimiseMaxDistance method and print the result
    long double ans = sol.minimiseMaxDistance(arr, k);
    cout << "The answer is: " << ans << "\n";

    return 0;
}
import java.util.*;

class Solution {
    /* Function to minimize the maximum
    distance between gas stations */
    public static double minimiseMaxDistance(int[] arr, int k) {
        int n = arr.length; 
        
        /* Array to store how many gas 
        stations are placed in each section*/
        int[] howMany = new int[n - 1];

        //Pick and place k gas stations
        for (int gasStations = 1; gasStations <= k; gasStations++) {
            
            double maxSection = -1;
            int maxInd = -1;
            
            /* Find the maximum section 
            and insert the gas station*/
            for (int i = 0; i < n - 1; i++) {
                double diff = arr[i + 1] - arr[i];
                double sectionLength = diff / (double)(howMany[i] + 1);
                
                /* Update the maximum section
                length and its index */
                if (sectionLength > maxSection) {
                    maxSection = sectionLength;
                    maxInd = i;
                }
            }
            /* Insert the current gas 
            station into the section */
            howMany[maxInd]++;
        }

        //Find the maximum distance i.e. the answer:
        double maxAns = -1;
        for (int i = 0; i < n - 1; i++) {
            double diff = arr[i + 1] - arr[i];
            double sectionLength =
                diff / (double)(howMany[i] + 1);
            maxAns = Math.max(maxAns, sectionLength);
        }
        return maxAns;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5};
        int k = 4;

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Call the minimiseMaxDistance method and print the result
        double ans = sol.minimiseMaxDistance(arr, k);
        System.out.println("The answer is: " + ans);
    }
}
class Solution:
    """ Function to minimize the maximum
    distance between gas stations """
    def minimiseMaxDistance(self, arr, k):
        n = len(arr)  
        howMany = [0] * (n - 1)

        # Pick and place k gas stations
        for gasStations in range(1, k + 1):
        
            maxSection = -1
            maxInd = -1
        
            """ Find the maximum section 
            and insert the gas station"""
            for i in range(n - 1):
                diff = arr[i + 1] - arr[i]
                sectionLength = diff / (howMany[i] + 1)
            
                """ Update the maximum section
                length and its index """
                if sectionLength > maxSection:
                    maxSection = sectionLength
                    maxInd = i
                  
            """ Insert the current gas 
            station into the section"""
            howMany[maxInd] += 1

        # Find the maximum distance i.e. the answer
        maxAns = -1
    
        for i in range(n - 1):
            diff = arr[i + 1] - arr[i]
            sectionLength = diff / (howMany[i] + 1)
            maxAns = max(maxAns, sectionLength)
        
        return maxAns

if __name__ == "__main__":
    arr = [1, 2, 3, 4, 5]
    k = 4

    # Create an instance of the Solution class
    sol = Solution()

    # Call the minimiseMaxDistance method and print the result
    ans = sol.minimiseMaxDistance(arr, k)
    print(f"The answer is: {ans:.6f}")
class Solution {
    /* Function to minimize the maximum
    distance between gas stations */
    minimiseMaxDistance(arr, k) {
    const n = arr.length; 
    
    /* Array to store how many gas 
        stations are placed in each section*/
    const howMany = new Array(n - 1).fill(0);

    //Pick and place k gas stations
    for (let gasStations = 1; gasStations <= k; gasStations++) {
        let maxSection = -1;
        let maxInd = -1;
        
        /* Find the maximum section 
        and insert the gas station*/
        for (let i = 0; i < n - 1; i++) {
            const diff = arr[i + 1] - arr[i];
            
            /* Update the maximum section
            length and its index */
            const sectionLength = diff / (howMany[i] + 1);
            if (sectionLength > maxSection) {
                maxSection = sectionLength;
                maxInd = i;
            }
        }
        /* Insert the current gas 
        station into the section */
        howMany[maxInd]++;
    }

    //Find the maximum distance i.e. the answer
    let maxAns = -1;
    for (let i = 0; i < n - 1; i++) {
        const diff = arr[i + 1] - arr[i];
        const sectionLength = diff / (howMany[i] + 1);
        maxAns = Math.max(maxAns, sectionLength);
    }
    return maxAns;
    }
}

const arr = [1, 2, 3, 4, 5];
const k = 4;

// Create an instance of the Solution class
const sol = new Solution();

// Call the minimiseMaxDistance method and print the result
const ans = sol.minimiseMaxDistance(arr, k);
console.log(`The answer is: ${ans}`);

Complexity Analysis:

Time Complexity:O(k*N) + O(N), N is size of the given array, k is number of gas stations to be placed. O(k*N) to insert k gas stations between the existing stations with maximum distance. Another O(N) for finding the answer i.e. the maximum distance.

Space Complexity: O(N-1), As an array is used to keep track of placed gas stations.

Intuition:

The idea here is to use the Heap data structure, which can be implemented as a Priority Queue, to solve the problem more efficiently. Instead of the brute-force approach where we iterate over each gas station to find the maximum distance to the next one, we can optimize this using a heap.

In a max heap implementation, the largest element is always at the root. This property allows us to efficiently retrieve the maximum distance. Store the elements in the heap as pairs, where each pair consists of the distance and its corresponding index. This way, we can keep track of the distances and their respective positions as we process each gas station.

By using a max heap (implemented via a priority queue), we avoid the need to iterate through the array multiple times to find the maximum distance manually. Instead, the heap structure inherently keeps track of the maximum distance, allowing us to place each gas station optimally.

Approach:

First, declare an array howMany of size n-1, to keep track of the number of placed gas stations and a priority queue that uses max heap, where n is the size of array provided in question.
Now, insert the first n-1 indices with the respective distance value, for every index.
Next, using a loop we will pick k gas stations one at a time. Then pick the first element of the priority queue as this is the element with the maximum distance. Let’s call the index ‘secInd’.
Now place the current gas station at ‘secInd’(howMany[secInd]++) and calculate the new section length. After that, again insert the pair(new section length, secInd) into the priority queue for further consideration.
After performing all the steps for k gas stations, the distance at the top of the priority queue will be the answer as we want the maximum distance.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to minimize the maximum
    distance between gas stations*/
    long double minimiseMaxDistance(vector<int> &arr, int k) {
        int n = arr.size(); 
        
        /* Array to store how many gas 
        stations are placed in each section*/
        vector<int> howMany(n - 1, 0); 
        
        /* Max heap to store sections by
        their current maximum distance*/
        priority_queue<pair<long double, int>> pq; 

        /* Insert first n-1 elements into priority
        queue with respective distance values*/
        for (int i = 0; i < n - 1; i++) {
            pq.push({(long double)(arr[i + 1] - arr[i]), i});
        }

        for (int gasStations = 1; gasStations <= k; gasStations++) {
            /* Find the maximum section 
            and insert the gas station*/
            auto tp = pq.top(); 
            pq.pop(); 
            
            // Index of the section
            int secInd = tp.second; 

            // Insert current gas station into section
            howMany[secInd]++;

            /* Calculate the initial difference
            between adjacent gas stations*/
            long double inidiff = (long double)(arr[secInd + 1] - arr[secInd]);

            /* Calculate the new section length 
            after inserting another gas station*/
            long double newSecLen = inidiff / (long double)(howMany[secInd] + 1);

            /* Push the updated section 
            back into the priority queue*/
            pq.push({newSecLen, secInd});
        }
        /* Return the maximum distance in
        the top section of the heap*/
        return pq.top().first; 
    }
};

int main() {
    vector<int> arr = {1, 2, 3, 4, 5};
    int k = 4;

    // Create an instance of the Solution class
    Solution sol;

    // Call the minimiseMaxDistance method and print the result
    long double ans = sol.minimiseMaxDistance(arr, k);
    cout << "The answer is: " << ans << "\n";

    return 0;
}
import java.util.PriorityQueue;

class Solution {
    /* Function to minimize the maximum
       distance between gas stations */
    public double minimiseMaxDistance(int[] arr, int k) {
        int n = arr.length; // Size of array
        
        /* Array to store how many gas 
           stations are placed in each section */
        int[] howMany = new int[n - 1]; 
        
        /* Max heap to store sections by
           their current maximum distance */
        PriorityQueue pq = new PriorityQueue<>((Pair a, Pair b) -> Double.compare(b.first, a.first));

        /* Insert first n-1 elements into priority
           queue with respective distance values */
        for (int i = 0; i < n - 1; i++) {
            pq.add(new Pair(arr[i + 1] - arr[i], i));
        }

        for (int gasStations = 1; gasStations <= k; gasStations++) {
            /* Find the maximum section 
               and insert the gas station */
            Pair tp = pq.poll();
            
            // Index of the section
            int secInd = tp.second;

            // Insert current gas station into section
            howMany[secInd]++;

            /* Calculate the initial difference
               between adjacent gas stations */
            double inidiff = arr[secInd + 1] - arr[secInd];

            /* Calculate the new section length 
               after inserting another gas station */
            double newSecLen = inidiff / (double) (howMany[secInd] + 1);

            /* Push the updated section 
               back into the priority queue */
            pq.add(new Pair(newSecLen, secInd));
        }

        /* Return the maximum distance in
        the top section of the heap */
        return pq.peek().first;
    }
    
    /* Nested Pair class */
    private static class Pair {
        double first;
        int second;

        Pair(double first, int second) {
            this.first = first;
            this.second = second;
        }
    }

    /* Main method for testing */
    public static void main(String[] args) {
        Solution solution = new Solution();
        
        int[] arr = {1, 2, 8, 10};
        int k = 3;

        double result = solution.minimiseMaxDistance(arr, k);
        System.out.println("Minimum Maximum Distance: " + result);
    }
}

import heapq

class Solution:
    """ Function to minimize the maximum
        distance between gas stations """
    def minimiseMaxDistance(self, arr, k):
        
        n = len(arr) 
        
        """ Array to store how many gas 
            stations are placed in each section """
        howMany = [0] * (n - 1)
        
        """ Min heap to store sections by
            their current maximum distance """
        pq = []

        """ Insert first n-1 elements into priority
            queue with respective distance values """
        for i in range(n - 1):
            heapq.heappush(pq, (-float(arr[i + 1] - arr[i]), i))

        for gasStations in range(1, k + 1):
            """ Find the maximum section 
                and insert the gas station """
            neg_dist, secInd = heapq.heappop(pq) 
            
             # Get the section with maximum distance
            max_dist = -neg_dist 
            
            # Insert current gas station into section
            howMany[secInd] += 1

            """ Calculate the initial difference
                between adjacent gas stations """
            inidiff = float(arr[secInd + 1] - arr[secInd])

            """ Calculate the new section length 
                after inserting another gas station """
            newSecLen = inidiff / (howMany[secInd] + 1)

            """ Push the updated section 
                back into the priority queue """
            heapq.heappush(pq, (-newSecLen, secInd))

        """ Return the maximum distance in
        the top section of the heap"""
        return -pq[0][0]

if __name__ == "__main__":
    arr = [1, 2, 3, 4, 5]
    k = 4

    # Create an instance of the Solution class
    sol = Solution()

    # Call the minimiseMaxDistance method and print the result
    ans = sol.minimiseMaxDistance(arr, k)
    print(f"The answer is: {ans}")
class Solution {
    /* Function to minimize the maximum
       distance between gas stations */
    minimiseMaxDistance(arr, k) {
        const n = arr.length; // Size of array
        
        /* Array to store how many gas 
           stations are placed in each section */
        const howMany = new Array(n - 1).fill(0); 
        
        /* Min heap to store sections by
           their current maximum distance */
        const pq = []; 

        /* Insert first n-1 elements into priority
           queue with respective distance values */
        for (let i = 0; i < n - 1; i++) {
            pq.push([- (arr[i + 1] - arr[i]), i]);
        }

        for (let gasStations = 1; gasStations <= k; gasStations++) {
            /* Find the maximum section 
               and insert the gas station */
            pq.sort((a, b) => b[0] - a[0]); 
            
            // Get the section with maximum distance
            const [negDist, secInd] = pq.pop(); 

            // Insert current gas station into section
            howMany[secInd]++;

            /* Calculate the initial difference
               between adjacent gas stations */
            const inidiff = arr[secInd + 1] - arr[secInd];

            /* Calculate the new section length 
               after inserting another gas station */
            const newSecLen = inidiff / (howMany[secInd] + 1);

            /* Push the updated section 
               back into the priority queue */
            pq.push([-newSecLen, secInd]);
        }

        /* Return the maximum distance in
        the top section of the heap*/
        return -pq[0][0];
    }
}

const arr = [1, 2, 3, 4, 5];
const k = 4;

// Create an instance of the Solution class
const sol = new Solution();

// Call the minimiseMaxDistance method and print the result
const ans = sol.minimiseMaxDistance(arr, k);
console.log(`The answer is: ${ans}`);

Complexity Analysis:

Time Complexity:O(NlogN + klogN), N is size of the given array, k = no. of gas stations to be placed. As, the insert operation of priority queue takes logN time complexity. O(NlogN) for inserting all the indices with distance values and O(klogN) for placing the gas stations.

Space Complexity:O(N-1)+O(N-1). The first O(N-1) is for the array to keep track of placed gas stations and the second one is for the priority queue.

Intuition:

The idea here is to use the Binary Search algorithm to optimize the approach. The primary objective of the Binary Search algorithm is to efficiently determine the appropriate half to eliminate, thereby reducing the search space by half. It does this by determining a specific condition that ensures that the target is not present in that half.

Observation:

Minimum possible answer: The minimum possible answer is obtained when all the gas stations are placed in a single location. In this case, the maximum distance will be 0.
Maximum possible answer: Stations will not be placed before the first or after the last station; instead, they will be placed in between the existing stations. Therefore, the maximum possible answer is determined by the maximum distance between two consecutive existing stations.
Upon closer observation, it can be recognized that the answer space ranges between [0, max(dist)] and it is sorted. Additionally, a pattern can be identified that allows the space to be divided into two halves: one consisting of potential answers and the other of non-viable options. Therefore, binary search will be applied on the answer space.

Changes in the binary search algorithm to apply it to the decimal answer space:

The traditional binary search algorithm used for integer answer space won't be effective in this case, as the answer space consists of decimal numbers. Changes need to be made to adjust some conditions to tailor the algorithm to this specific context. These changes are as follows:
The condition 'while(low <= high)' inside the 'while' loop won't work for decimal answers and might lead to a TLE (Time Limit Exceeded) error. To avoid this, the condition can be modified to 'while(high - low > 10^(-6))'. This ensures that only differences up to the 6th decimal place are considered. Any differences beyond this decimal precision won't be taken into account, as answers within 10^-6 of the actual answer are explicitly accepted by the question.
The operation 'low = mid + 1' is used to eliminate the left half. However, to ensure that we do not skip over potential decimal numbers and possibly miss the actual answer, 'low = mid' will be used instead.
Similarly, the operation 'high = mid - 1' is used to eliminate the right half. However, to ensure that potential decimal numbers are not overlooked and that the actual answer is not missed, 'high = mid' will be used instead.<.li>

Approach:

Binary search is being applied on the answer, specifically on the possible values of distances. Therefore, a method needs to be devised to determine the number of gas stations that can be placed for a particular value of distance.

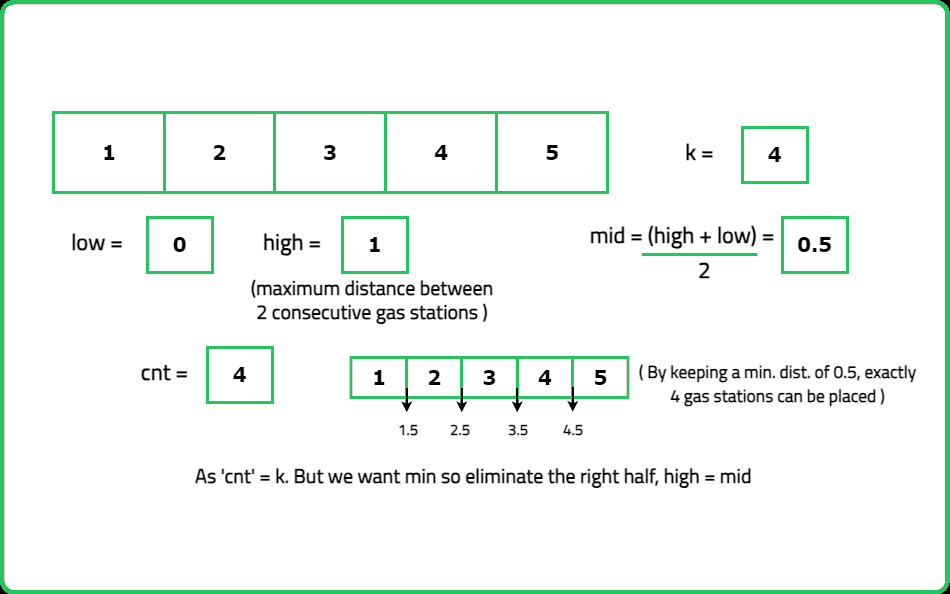
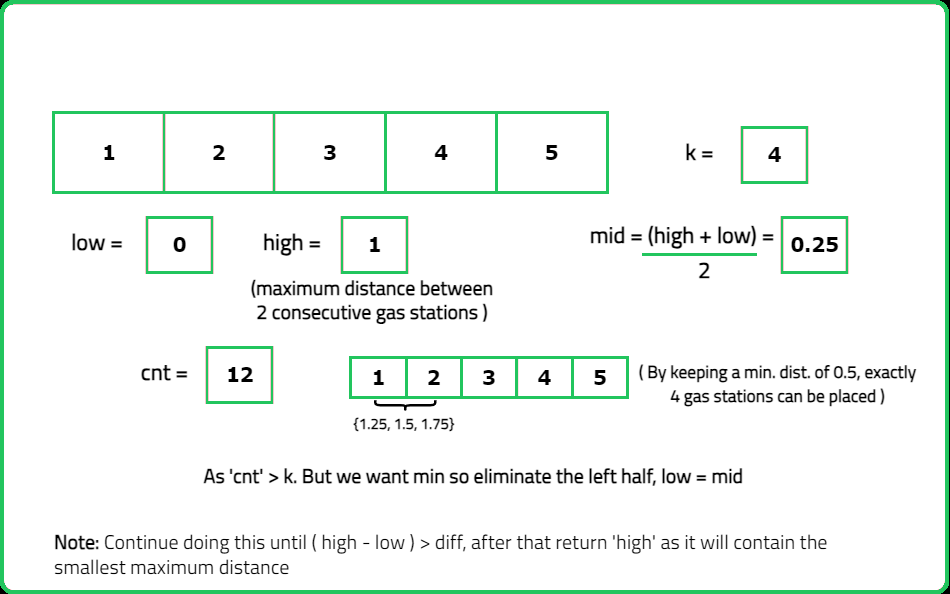
Working of minimiseMaxDistance(arr, k):

The maximum distance between two consecutive gas stations, denoted as max(dist), is first determined.
Pointers, denoted as low and high, are initially positioned. Low points to 0, and high points to max(dist).
Employ the while with the condition ‘while(high - low > 10^(-6))’. Within the loop, the value of ‘mid’ is calculated using the formula mid = (low + high) / 2.0.
Invoke the ‘numberOfGasStationsRequired()’ function with ‘mid’ as the potential distance value to determine the number of gas stations that can be placed.
If the result returned by the function is greater than k, the left half is eliminated (low = mid). Otherwise, the right half is eliminated (high = mid).
Finally, outside the loop, return either low or high as their difference is less than or equal to 10^(-6), both potentially representing the answer. Here, 'high' is returned as the chosen possible answer.

Working of numberOfGasStationsRequired(dist, arr):

First, initialize few variables: 'n' stores the size of the vector arr and 'cnt' is initialized to count the number of gas stations required.
Iterate through the array and for each pair of consecutive elements, calculate the 'numberInBetween', which represents the number of gas stations needed between these two points. This gives an estimate of how many stations would be needed if they were evenly spaced along the distance 'dist'.
If the actual distance calculated perfectly matches (dist * numberInBetween), adjust 'numberInBetween' by subtracting 1. This adjustment is intended to handle cases where the distance exactly matches the spacing defined by 'dist'. Otherwise increase the 'cnt' by 'numberInBetween'. Finally return 'cnt' variable.

Please refer to the video for complete dry run.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to calculate the number of gas 
    stations required for given distance*/
    int numberOfGasStationsRequired(long double dist, vector<int> &arr) {
        // Size of the array
        int n = arr.size(); 
        int cnt = 0;
        for (int i = 1; i < n; i++) {
            
            /* Calculate number of gas stations
            needed between two points*/
            int numberInBetween = ((arr[i] - arr[i - 1]) / dist);
            
            // Adjust if exact distance fits perfectly
            if ((arr[i] - arr[i - 1]) == (dist * numberInBetween)) {
                numberInBetween--;
            }
            
            cnt += numberInBetween;
        }
        return cnt;
    }
public:
    /* Function to minimize the maximum
    distance between gas stations*/
    long double minimiseMaxDistance(vector<int> &arr, int k) {
        int n = arr.size(); 
        long double low = 0;
        long double high = 0;

        /* Find the maximum distance between
        consecutive gas stations*/
        for (int i = 0; i < n - 1; i++) {
            high = max(high, (long double)(arr[i + 1] - arr[i]));
        }

        /* Apply Binary search to find the 
        minimum possible maximum distance*/
        long double diff = 1e-6;
        while (high - low > diff) {
            long double mid = (low + high) / 2.0;
            int cnt = numberOfGasStationsRequired(mid, arr);

            /* Adjust the search range based on 
            the number of gas stations required*/
            if (cnt > k) {
                low = mid;
            } else {
                high = mid;
            }
        }

        // Return the smallest maximum distance found
        return high;
    }
};

int main() {
    vector<int> arr = {1, 2, 3, 4, 5};
    int k = 4;

    // Create an instance of the Solution class
    Solution sol;

    // Call the minimiseMaxDistance method and print the result
    long double ans = sol.minimiseMaxDistance(arr, k);
    cout << "The answer is: " << ans << "\n";

    return 0;
}
import java.util.*;

class Solution {
    /* Function to calculate the number of gas
    stations required for given distance*/
    private int numberOfGasStationsRequired(double dist, int[] arr) {
        // Size of the array
        int n = arr.length;
        int cnt = 0;
        for (int i = 1; i < n; i++) {
            
            /* Calculate number of gas stations
            needed between two points*/
            int numberInBetween = (int) ((arr[i] - arr[i - 1]) / dist);

            // Adjust if exact distance fits perfectly
            if ((arr[i] - arr[i - 1]) == (dist * numberInBetween)) {
                numberInBetween--;
            }

            cnt += numberInBetween;
        }
        return cnt;
    }

    /* Function to minimize the maximum 
    distance between gas stations*/
    public double minimiseMaxDistance(int[] arr, int k) {
        int n = arr.length; 
        double low = 0;
        double high = 0;

        /* Find the maximum distance between
        consecutive gas stations*/
        for (int i = 0; i < n - 1; i++) {
            high = Math.max(high, arr[i + 1] - arr[i]);
        }

        /* Apply Binary search to find the 
        minimum possible maximum distance*/
        double diff = 1e-6;
        while (high - low > diff) {
            double mid = (low + high) / 2.0;
            int cnt = numberOfGasStationsRequired(mid, arr);

            /* Adjust the search range based on
            the number of gas stations required*/
            if (cnt > k) {
                low = mid;
            } else {
                high = mid;
            }
        }

        // Return smallest maximum distance found
        return high;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5};
        int k = 4;

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Call the minimiseMaxDistance method and print the result
        double ans = sol.minimiseMaxDistance(arr, k);
        System.out.println("The answer is: " + ans);
    }
}
import math

class Solution:
    # Function to calculate the number of gas 
    # stations required for given distance
    def numberOfGasStationsRequired(self, dist, arr):
        n = len(arr)
        cnt = 0
        for i in range(1, n):
            # Calculate number of gas stations 
            # needed between two points
            numberInBetween = (arr[i] - arr[i - 1]) / dist
            
            # Adjust if exact distance fits perfectly
            if (arr[i] - arr[i - 1]) == (dist * int(numberInBetween)):
                numberInBetween -= 1

            cnt += int(numberInBetween)
        return cnt

    # Function to minimize the maximum 
    # distance between gas stations
    def minimiseMaxDistance(self, arr, k):
        n = len(arr)
        low = 0
        high = 0

        # Find the maximum distance between 
        # consecutive gas stations
        for i in range(n - 1):
            high = max(high, arr[i + 1] - arr[i])

        # Apply Binary search to find the 
        # minimum possible maximum distance
        diff = 1e-6
        while high - low > diff:
            mid = (low + high) / 2.0
            cnt = self.numberOfGasStationsRequired(mid, arr)

            # Adjust the search range based on the 
            # number of gas stations required
            if cnt > k:
                low = mid
            else:
                high = mid

        # Return the smallest maximum distance found
        return high


if __name__ == "__main__":
    arr = [1, 2, 3, 4, 5]
    k = 4

    # Create an instance of the Solution class
    sol = Solution()

    # Call the minimiseMaxDistance method and print the result
    ans = sol.minimiseMaxDistance(arr, k)
    print(f"The answer is: {ans}")
class Solution {
    /* Function to calculate the number of 
    gas stations required for given distance*/
    numberOfGasStationsRequired(dist, arr) {
        
        // Size of the array
        const n = arr.length;
        let cnt = 0;
        for (let i = 1; i < n; i++) {
            
            /* Calculate number of gas stations
            needed between two points*/
            const numberInBetween = Math.floor((arr[i] - arr[i - 1]) / dist);
            
            // Adjust if exact distance fits perfectly
            if ((arr[i] - arr[i - 1]) === dist * numberInBetween) {
                cnt += numberInBetween - 1;
            } else 
                cnt += numberInBetween;
        }
        return cnt;
    }

    /* Function to minimize the maximum 
    distance between gas stations*/
    minimiseMaxDistance(arr, k) {
        const n = arr.length; 
        let low = 0;
        let high = 0;

        /* Find the maximum distance between
        consecutive gas stations*/
        for (let i = 0; i < n - 1; i++) {
            high = Math.max(high, arr[i + 1] - arr[i]);
        }

        const diff = 1e-6;
        /* Apply Binary search to find the
        minimum possible maximum distance*/
        while (high - low > diff) {
            const mid = (low + high) / 2.0;
            const cnt = this.numberOfGasStationsRequired(mid, arr);

            /* Adjust the search range based on
            the number of gas stations required*/
            if (cnt > k) {
                low = mid;
            } else {
                high = mid;
            }
        }

        // Return smallest maximum distance found
        return high;
    }
}

const arr = [1, 2, 3, 4, 5];
const k = 4;

// Create an instance of the Solution class
const sol = new Solution();

// Call the minimiseMaxDistance method and print the result
const ans = sol.minimiseMaxDistance(arr, k);
console.log(`The answer is: ${ans}`);

Complexity Analysis:

Time Complexity:O(N*log(Len)) + O(N), N is size of the given array, Len is length of the answer space. Binary search is being applied on the answer space. For every possible answer, the function numberOfGasStationsRequired() is called, which has a time complexity of O(N). Additionally, O(N) time complexity is incurred initially for finding the maximum distance.

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Problem List

Minimise max distance to gas stations

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code