Detect a loop in LL
Given the head of a singly linked list. Return true if a loop exists in the linked list or return false.
A loop exists in a linked list if some node in the list can be reached again by continuously following the next pointer.
Internally, pos is used to denote the index(0-based) of the node from where the loop starts. Note that pos is not passed as a parameter.
Examples:
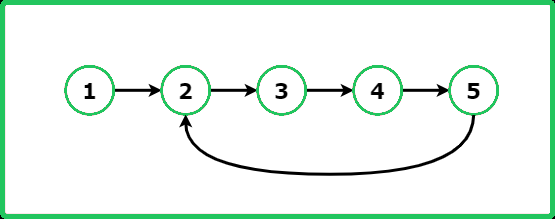
Input: head -> 1 -> 2 -> 3 -> 4 -> 5, pos = 1
Output: true
Explanation: The tail of the linked list connects to the node at 1st index.
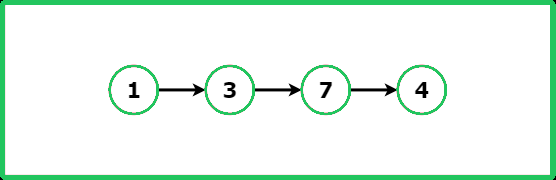
Input: head -> 1 -> 3 -> 7 -> 4, pos = -1
Output: false
Explanation: No loop is present in the linked list.
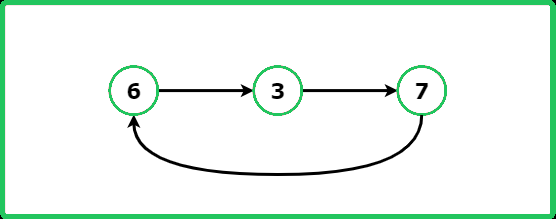
Input: head -> 6 -> 3 -> 7, pos = 0
Constraints
- 0 <= number of nodes in the cycle <= 105
- 0 <= ListNode.val <= 104
- pos is -1 or a valid index in the linked list
Hints
- A brute-force approach would use a hash set (O(n) space) to track visited nodes and detect a loop.
- The Floyd’s Tortoise and Hare Algorithm uses: A slow pointer (slow) → moves one step at a time. A fast pointer (fast) → moves two steps at a time.
Company Tags
Editorial
Intuition
A loop in a linked list happens when a node points back to one of the previous nodes, creating a cycle. This means that if you keep following the next pointers, you will eventually return to the same node. One common way to do this is by using hashing.

Approach
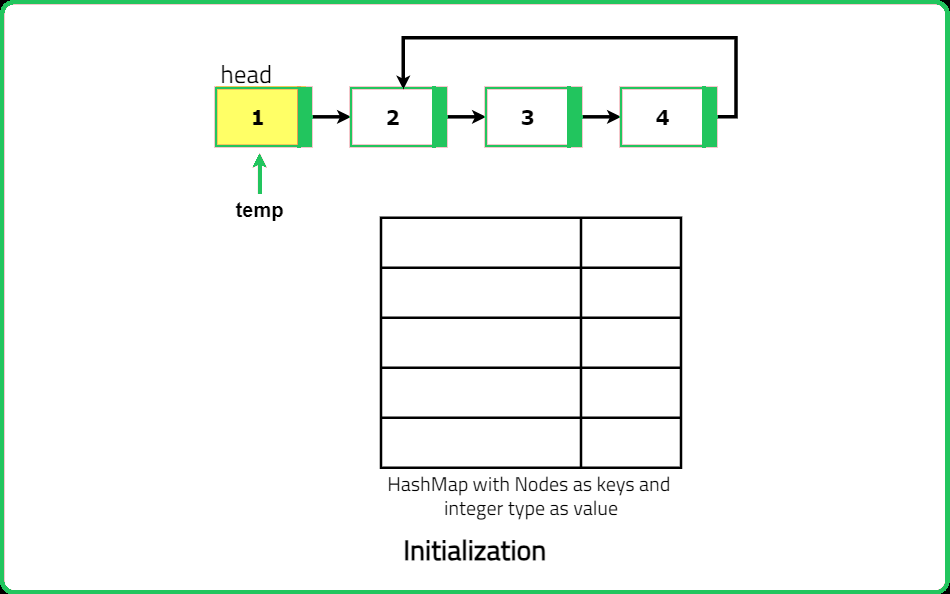
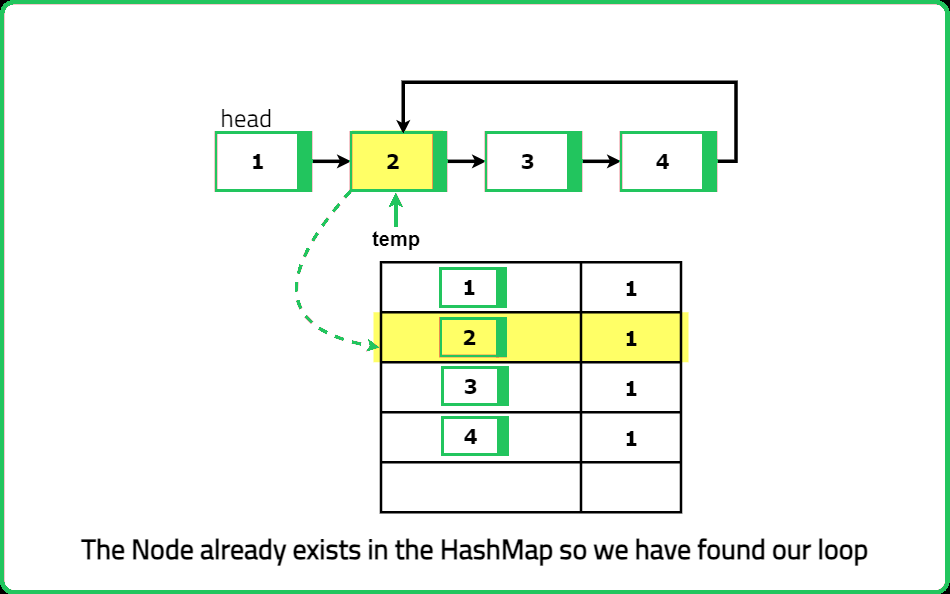
Initialization: Start by initializing a hash map to store the nodes we visit. Set a temporary pointer to the head of the linked list.
Traverse the List: Traverse through the linked list using the temporary pointer. For each node, check if it is already in the hash map. If the node is not in the hash map, add it to the map and move to the next node. If the node is already in the hash map, this means we have encountered a node we have seen before, indicating the presence of a loop.
Loop Detection: During the traversal, if we find a node that is already in the hash map, return true immediately because this confirms the existence of a loop.
End of List: If we reach the end of the linked list (i.e., the temporary pointer becomes null) without encountering any repeated nodes, it means there is no loop in the list. In this case, return false.
Dry Run
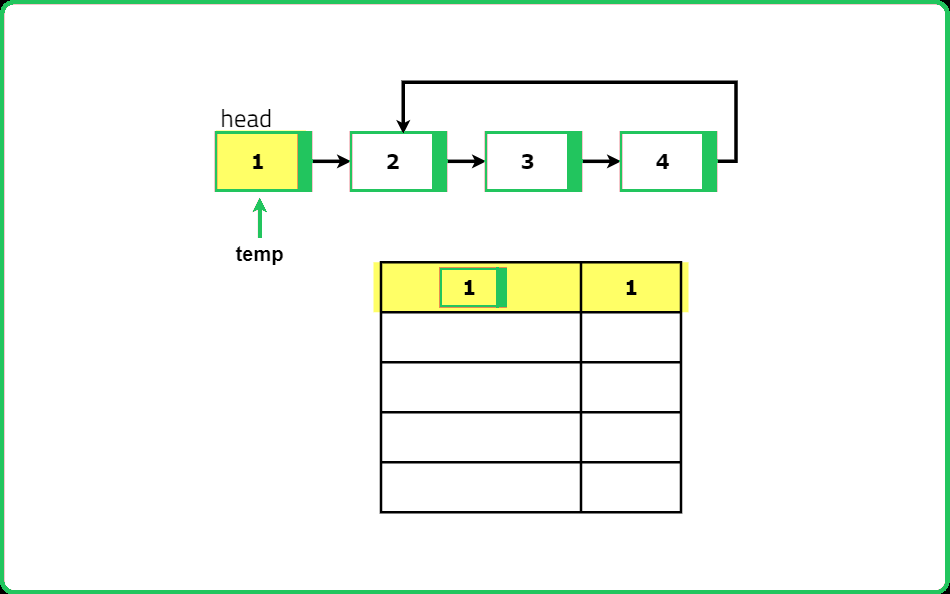
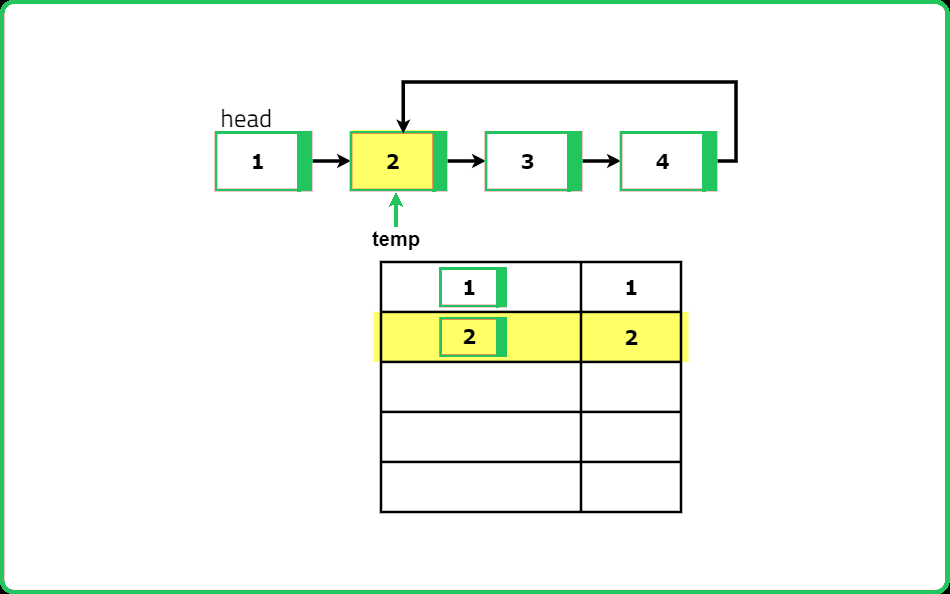
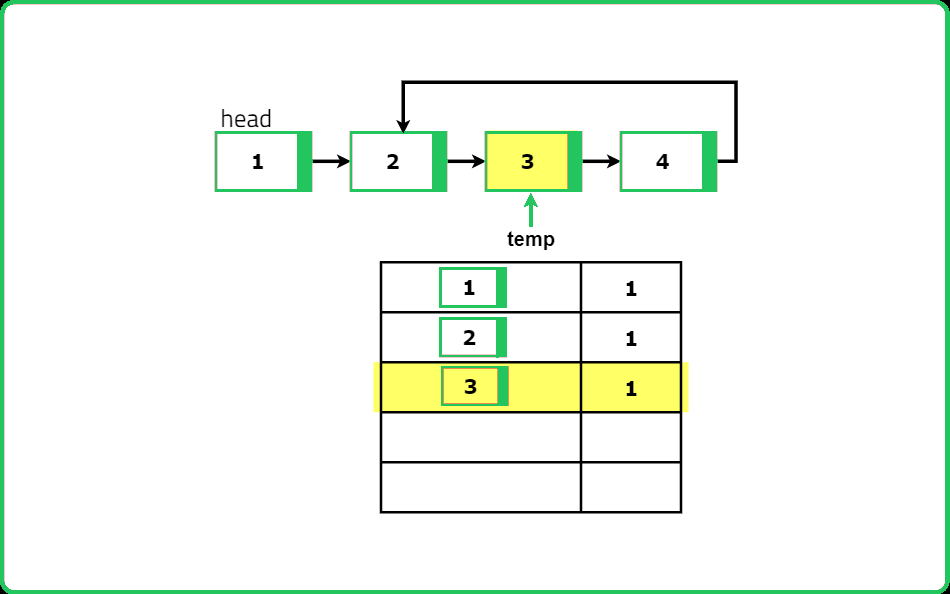
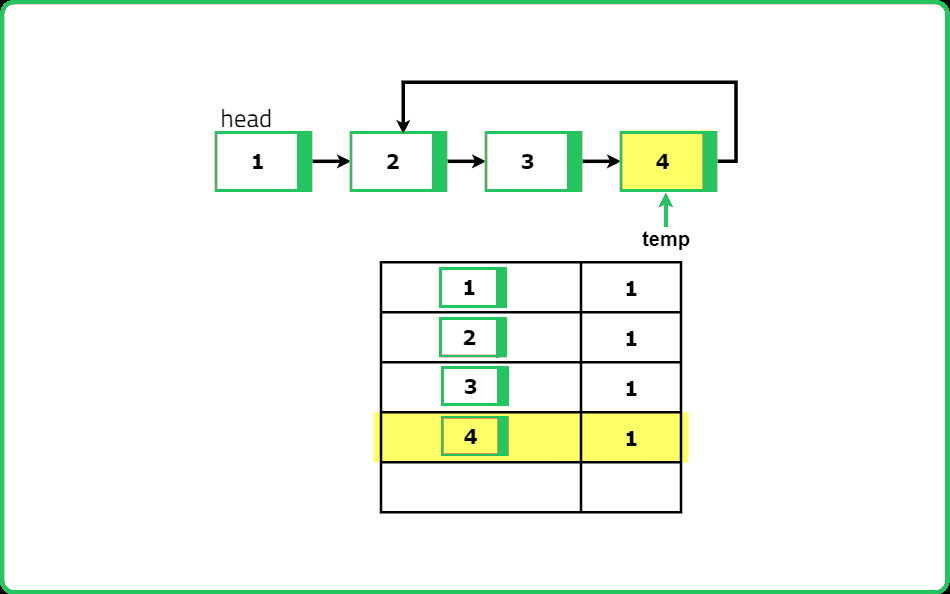






#include <iostream>
#include <unordered_map>
using namespace std;
//Definition of singly linked list:
struct ListNode
{
int val;
ListNode *next;
ListNode()
{
val = 0;
next = NULL;
}
ListNode(int data1)
{
val = data1;
next = NULL;
}
ListNode(int data1, ListNode *next1)
{
val = data1;
next = next1;
}
};
class Solution {
public:
// Function to detect a loop in the linked list
bool hasCycle(ListNode *head) {
// Initialize a pointer 'temp'
// At the head of the linked list
ListNode* temp = head;
// Create a map to keep track of
// Encountered nodes
std::unordered_map<ListNode*, int> nodeMap;
// Traverse the linked list
while (temp != nullptr) {
// If the node is already in the
// Map, there is a loop
if (nodeMap.find(temp) != nodeMap.end()) {
return true;
}
// Store the current node
// In the map
nodeMap[temp] = 1;
// Move to the next node
temp = temp->next;
}
// If the list is successfully traversed
// Without a loop, return false
return false;
}
};
// Function to print the linked list
void printLinkedList(ListNode* head) {
ListNode* temp = head;
// Traverse the linked list and print each node's value
while (temp != nullptr) {
std::cout << temp->val << " ";
temp = temp->next;
}
std::cout << std::endl;
}
int main() {
// Create a sample linked list
// With a loop for testing
ListNode* head = new ListNode(1);
ListNode* second = new ListNode(2);
ListNode* third = new ListNode(3);
ListNode* fourth = new ListNode(4);
ListNode* fifth = new ListNode(5);
head->next = second;
second->next = third;
third->next = fourth;
fourth->next = fifth;
// Create a loop
fifth->next = third;
Solution sol;
// Check if there is a loop
// In the linked list
if (sol.hasCycle(head)) {
cout << "Loop detected in the linked list." << endl;
} else {
cout << "No loop detected in the linked list." << endl;
}
// Clean up memory (free the allocated nodes)
delete head;
delete second;
delete third;
delete fourth;
delete fifth;
return 0;
}
import java.util.HashMap;
//Definition of Linked List
class ListNode {
int val;
ListNode next;
ListNode() {
val = 0;
next = null;
}
ListNode(int data1) {
val = data1;
next = null;
}
ListNode(int data1, ListNode next1) {
val = data1;
next = next1;
}
}
class Solution {
// Function to detect a loop in the linked list
public boolean hasCycle(ListNode head) {
// Initialize a pointer 'temp'
// At the head of the linked list
ListNode temp = head;
// Create a map to keep track of
// Encountered nodes
HashMap<ListNode, Integer> nodeMap = new HashMap<>();
// Traverse the linked list
while (temp != null) {
// If the node is already in the
// Map, there is a loop
if (nodeMap.containsKey(temp)) {
return true;
}
// Store the current node
// In the map
nodeMap.put(temp, 1);
// Move to the next node
temp = temp.next;
}
// If the list is successfully traversed
// Without a loop, return false
return false;
}
// Function to print the linked list
public void printLinkedList(ListNode head) {
ListNode temp = head;
// Traverse the linked list and print each node's value
while (temp != null) {
System.out.print(temp.val + " ");
temp = temp.next;
}
System.out.println();
}
public static void main(String[] args) {
// Create a sample linked list
// With a loop for testing
ListNode head = new ListNode(1);
ListNode second = new ListNode(2);
ListNode third = new ListNode(3);
ListNode fourth = new ListNode(4);
ListNode fifth = new ListNode(5);
head.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
// Create a loop
fifth.next = third;
Solution sol = new Solution();
// Check if there is a loop
// In the linked list
if (sol.hasCycle(head)) {
System.out.println("Loop detected in the linked list.");
} else {
System.out.println("No loop detected in the linked list.");
}
}
}
# Definition of singly linked list:
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
# Function to detect a loop in the linked list
def hasCycle(self, head):
# Initialize a pointer 'temp'
# At the head of the linked list
temp = head
# Create a set to keep track of
# Encountered nodes
nodeSet = set()
# Traverse the linked list
while temp is not None:
# If the node is already in the
# Set, there is a loop
if temp in nodeSet:
return True
# Store the current node
# In the set
nodeSet.add(temp)
# Move to the next node
temp = temp.next
# If the list is successfully traversed
# Without a loop, return False
return False
# Function to print the linked list
def printLinkedList(head):
temp = head
# Traverse the linked list and print each node's value
while temp is not None:
print(temp.val, end=" ")
temp = temp.next
print()
def main():
# Create a sample linked list
# With a loop for testing
head = ListNode(1)
second = ListNode(2)
third = ListNode(3)
fourth = ListNode(4)
fifth = ListNode(5)
head.next = second
second.next = third
third.next = fourth
fourth.next = fifth
# Create a loop
fifth.next = third
sol = Solution()
# Check if there is a loop
# In the linked list
if sol.hasCycle(head):
print("Loop detected in the linked list.")
else:
print("No loop detected in the linked list.")
if __name__ == "__main__":
main()
//Definition of singly linked list:
class ListNode {
constructor(val = 0, next = null) {
this.val = val;
this.next = next;
}
}
class Solution {
// Function to detect a loop in the linked list
hasCycle(head) {
// Initialize a pointer 'temp'
// At the head of the linked list
let temp = head;
// Create a set to keep track of
// Encountered nodes
let nodeSet = new Set();
// Traverse the linked list
while (temp !== null) {
// If the node is already in the
// Set, there is a loop
if (nodeSet.has(temp)) {
return true;
}
// Store the current node
// In the set
nodeSet.add(temp);
// Move to the next node
temp = temp.next;
}
// If the list is successfully traversed
// Without a loop, return false
return false;
}
}
// Function to print the linked list
function printLinkedList(head) {
let temp = head;
// Traverse the linked list and print each node's value
while (temp !== null) {
process.stdout.write(temp.val + " ");
temp = temp.next;
}
console.log();
}
// Main function
function main() {
// Create a sample linked list
// With a loop for testing
let head = new ListNode(1);
let second = new ListNode(2);
let third = new ListNode(3);
let fourth = new ListNode(4);
let fifth = new ListNode(5);
head.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
// Create a loop
fifth.next = third;
let sol = new Solution();
// Check if there is a loop
// In the linked list
if (sol.hasCycle(head)) {
console.log("Loop detected in the linked list.");
} else {
console.log("No loop detected in the linked list.");
}
}
// Call the main function to start the program
main();
Complexity Analysis
Time Complexity: O(N * 2 * log(N)) The algorithm traverses the linked list once, performing hashmap insertions and searches in the while loop for each node. The insertion and search operations in the unordered_map have a worst-case time complexity of O(log(N)). As the loop iterates through N nodes, the total time complexity is determined by the product of the traversal (O(N)) and the average-case complexity of the hashmap operations (insert and search), resulting in O(N * 2 * log(N)).
Space Complexity: O(N) The code uses a hashmap/dictionary to store encountered nodes, which can take up to O(N) additional space, where 'N' is the number of nodes in the list. Hence, the space complexity is O(N) due to the use of the map to track nodes.
Intuition
In a linked list with a loop, we can use two pointers to detect the cycle: one moves one node at a time (slow) and the other moves two nodes at a time (fast). As these pointers start moving through the list, they will eventually enter the loop and end up some distance 'd' apart within the loop.
The key idea is to observe the relative speeds of these pointers. Since the fast pointer moves twice as fast as the slow pointer, it reduces the distance between them by one node with each iteration. This is akin to a faster runner catching up to a slower runner in a race, where the faster runner closes the gap between them steadily.
In the context of the linked list, the fast pointer will eventually catch up to the slow pointer within the loop, thereby confirming the presence of a cycle. This happens because the fast pointer, moving at double the speed, progressively shortens the distance until it becomes zero.
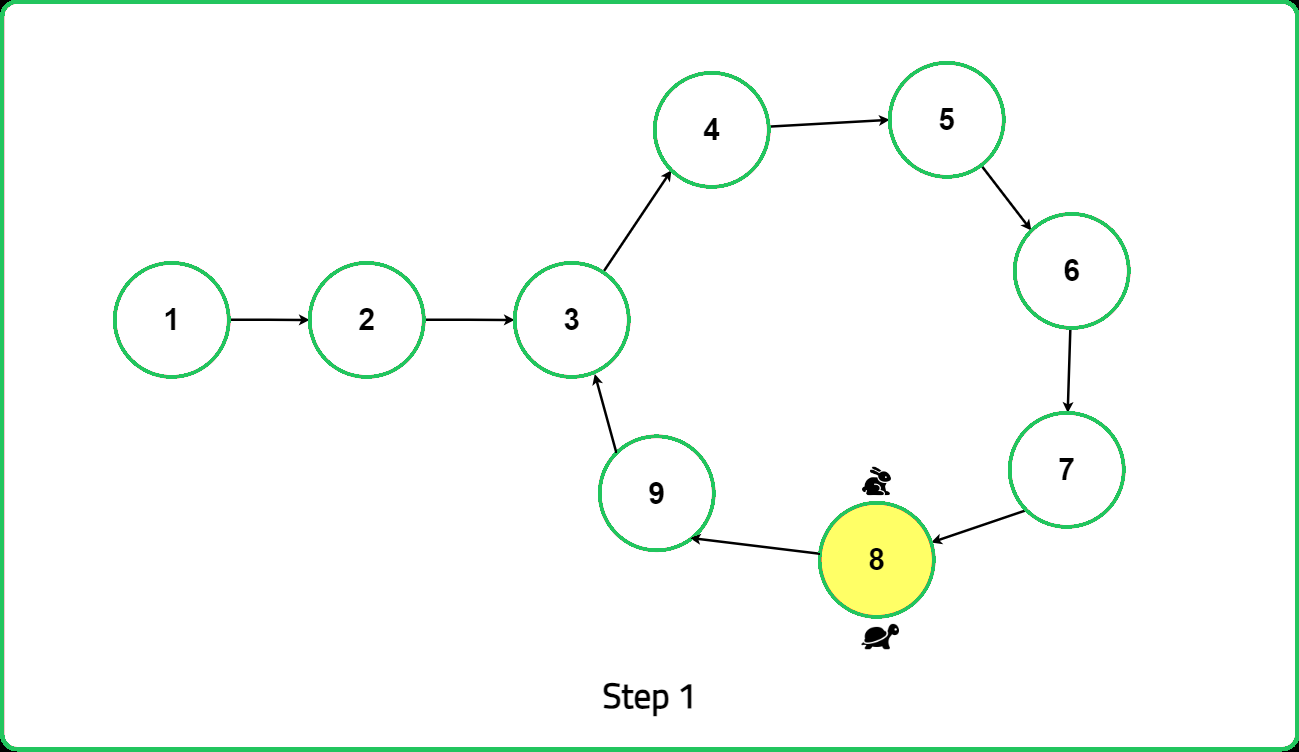
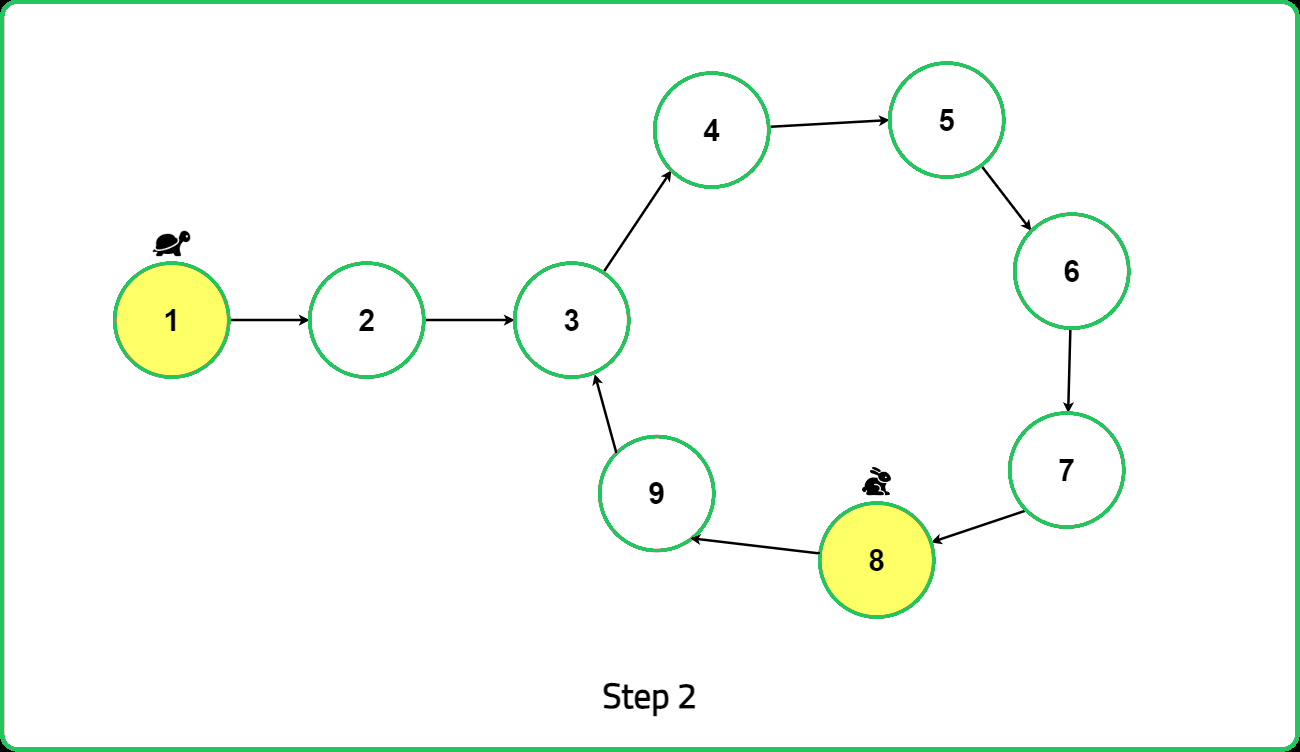
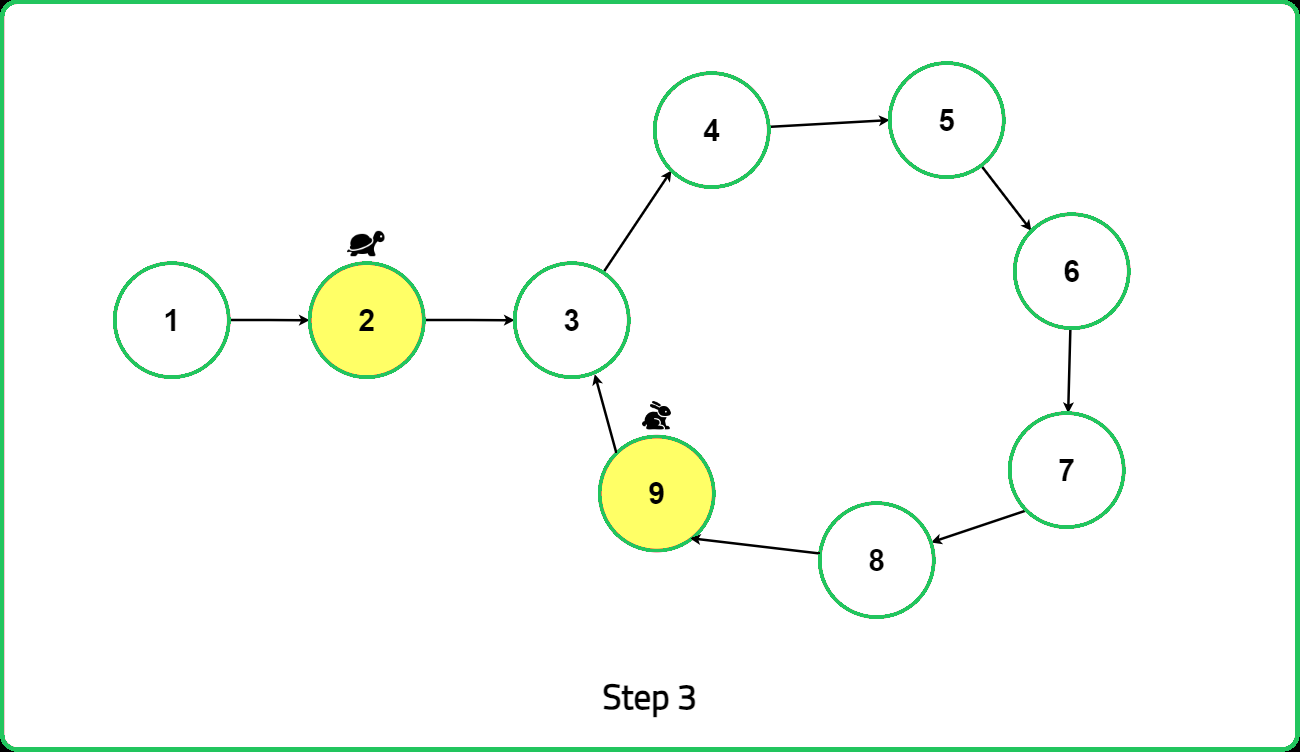
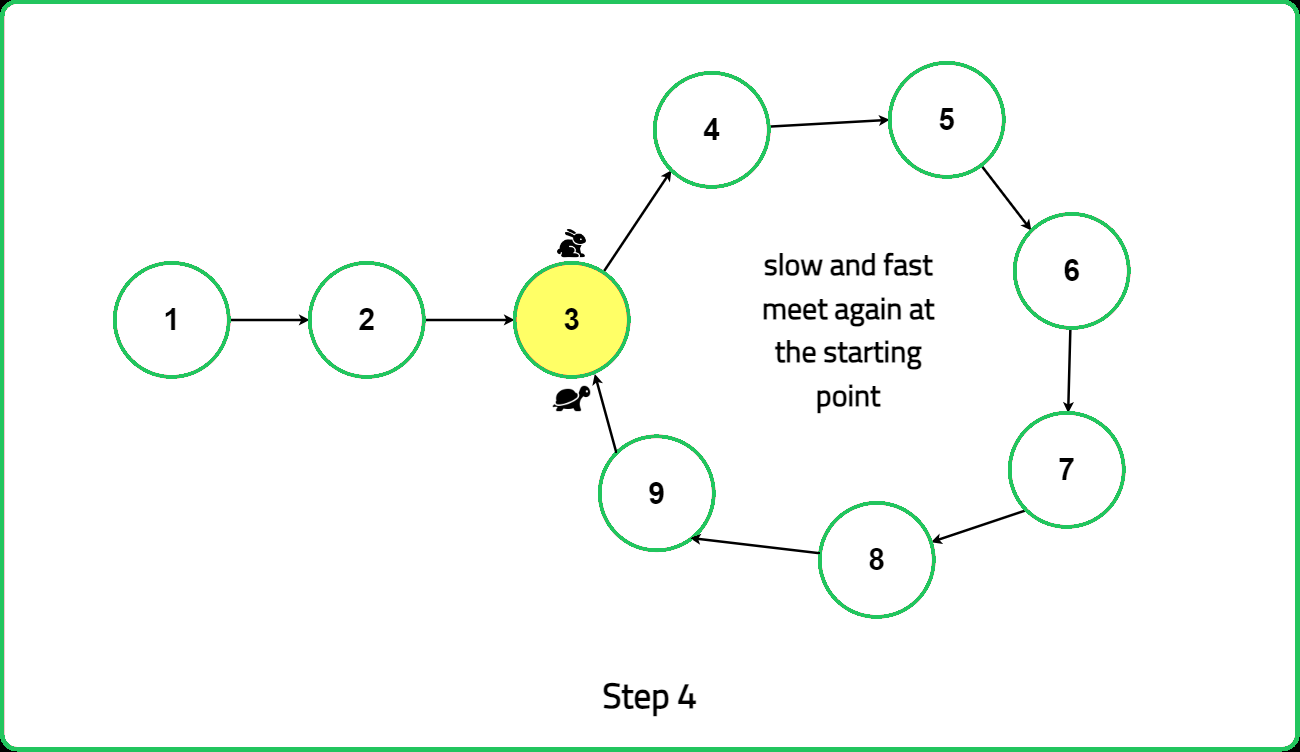




Proof of Intuition:
Let 'd' represent the initial distance between the slow and fast pointers inside the loop. With each step, the fast pointer moves ahead by two nodes while the slow pointer advances by one node.
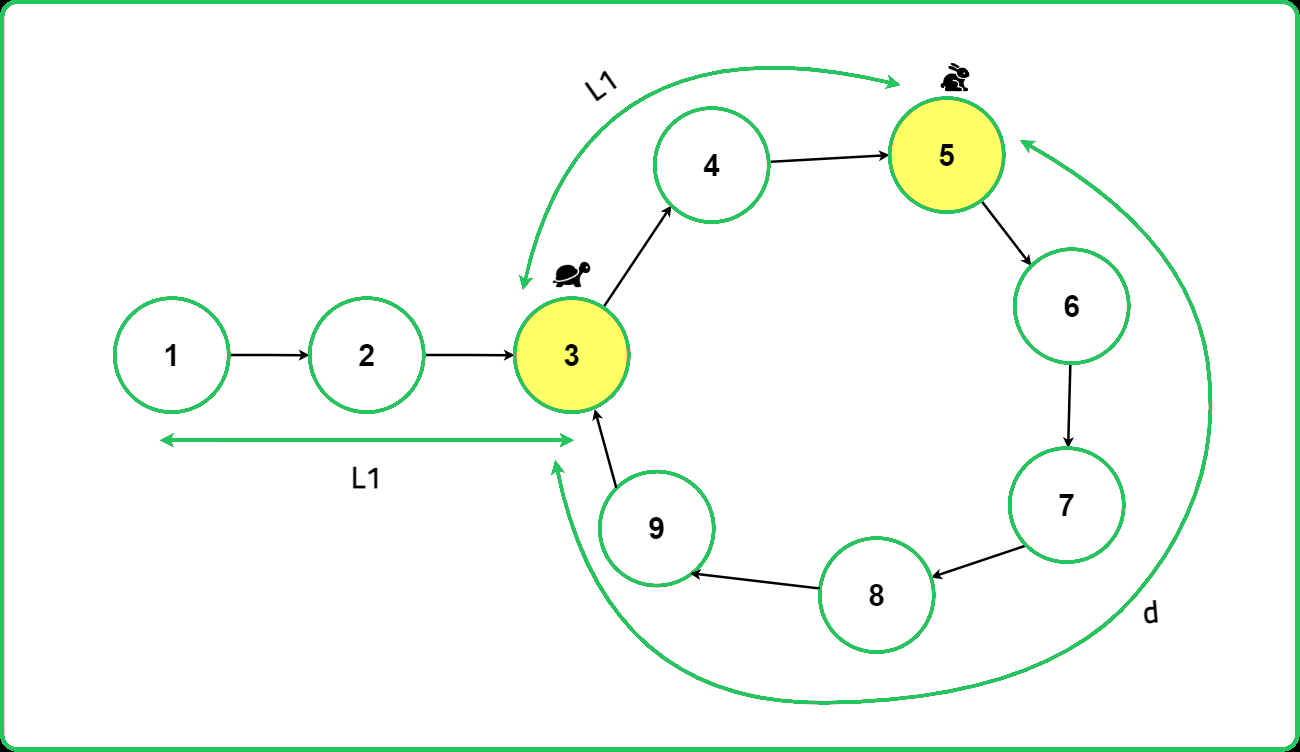
The difference in their speeds causes the gap to decrease by one node in each iteration (the fast pointer moves two nodes ahead while the slow pointer moves one node). This steady reduction ensures that the distance between their positions decreases consistently. Mathematically, since the fast pointer gains ground at twice the speed of the slow pointer, the gap between them shrinks by one node after each step. As a result, this decreasing distance continues until it eventually becomes zero.
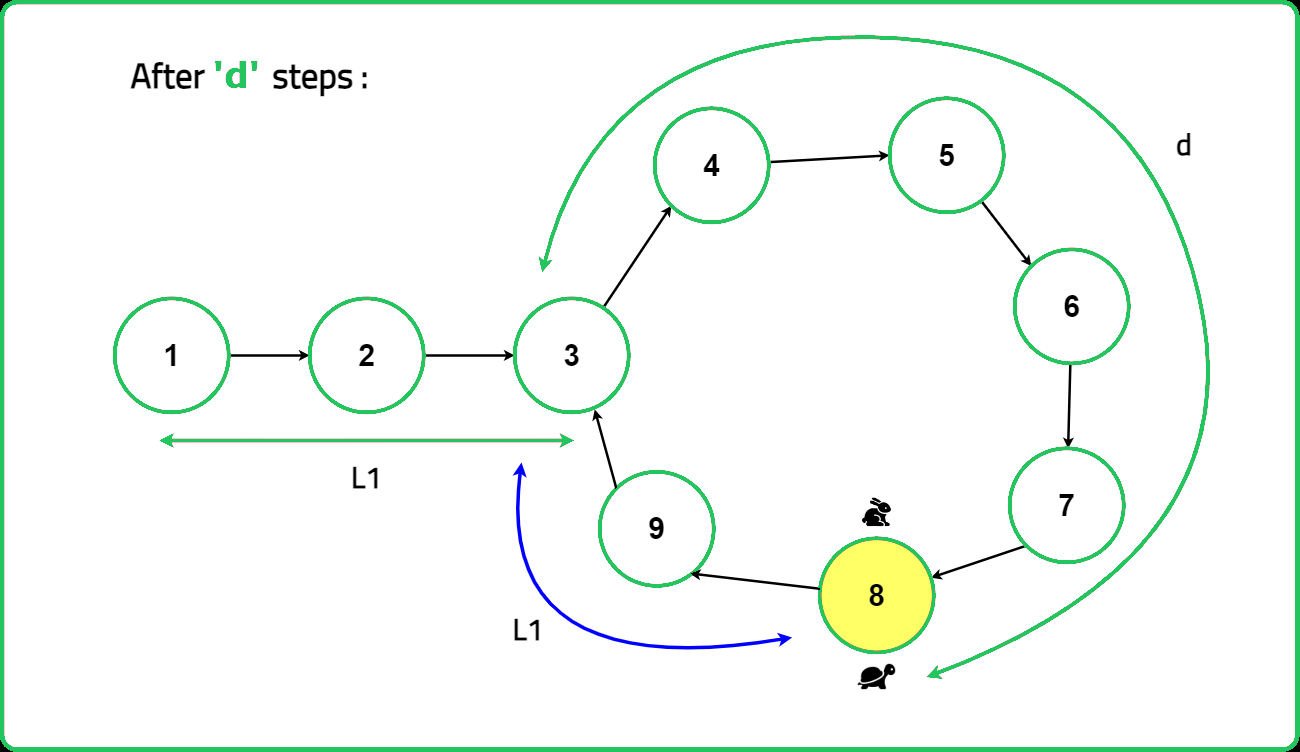


Therefore, the proof is in this iterative process where the faster movement of the fast pointer leads to a continual decrease in the gap distance, ultimately causing the two pointers to meet within the looped linked list.
Approach
The Tortoise and Hare technique is an efficient way to detect a loop in a linked list using two pointers with different speeds.
Initialization: Start by initializing two pointers, slow and fast, both pointing to the head of the linked list. The slow pointer moves one step at a time, while the fast pointer moves two steps at a time.
Traversal: As these pointers traverse the linked list, slow moves one node at a time, and fast moves two nodes at a time.
Conditions to Check:
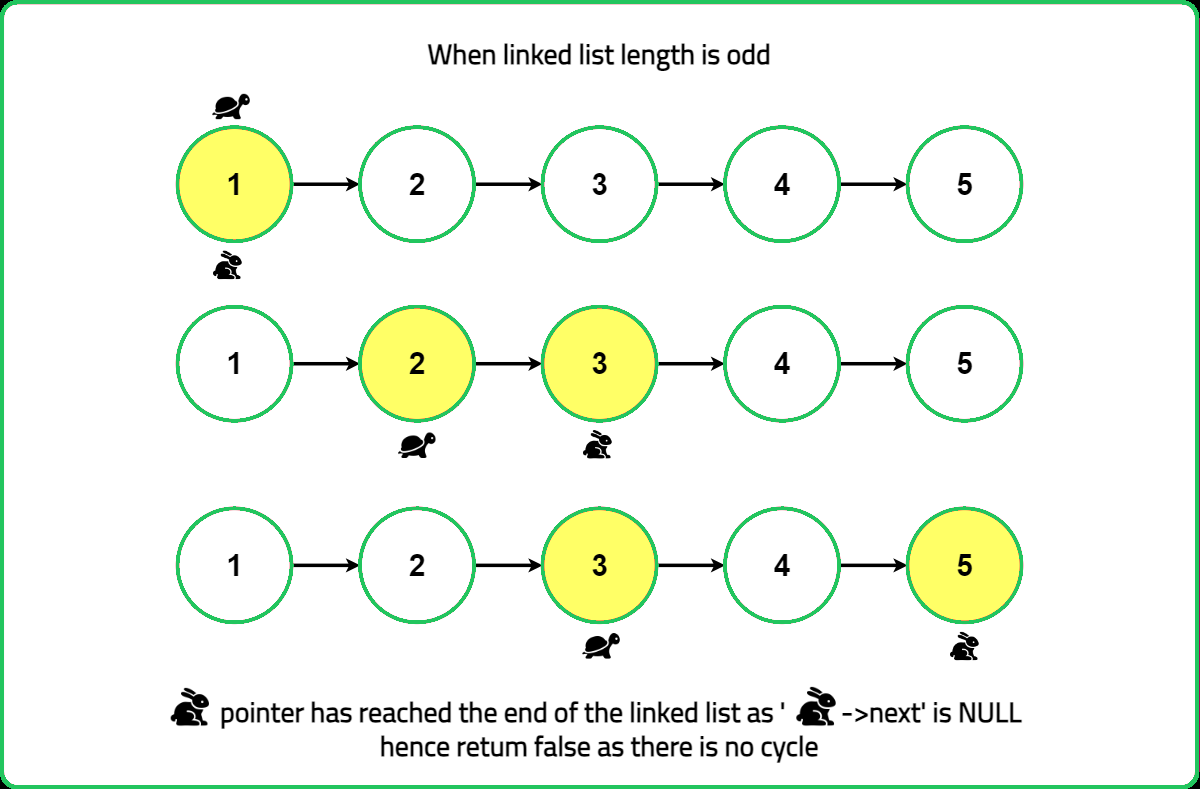
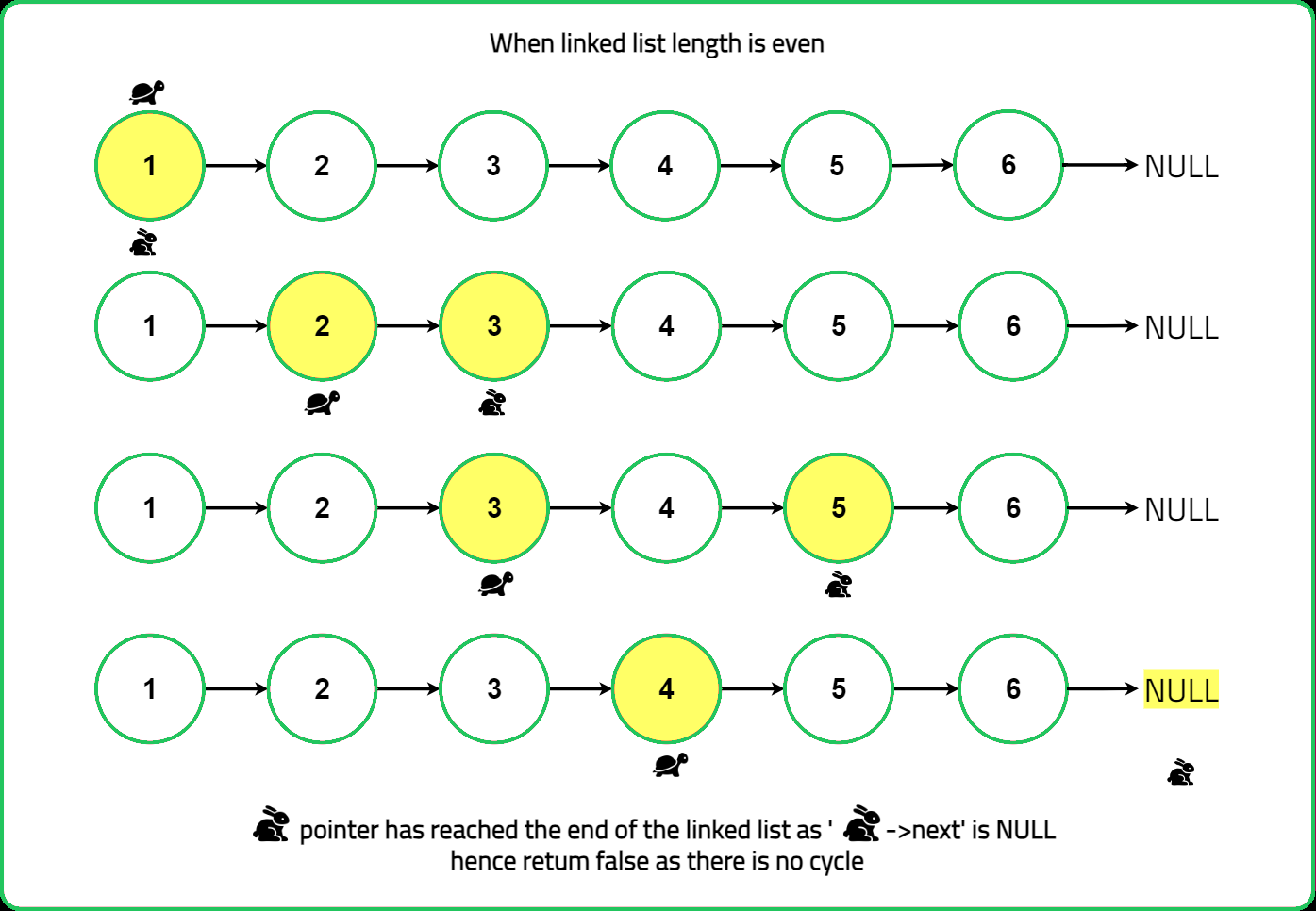
- If the
fastpointer or its next node (fast.next) becomes null, the linked list does not have a loop (i.e., it is linear). In this case, the algorithm will terminate and returnfalse. - If the
fastpointer catches up to theslowpointer and they meet at the same node, it indicates the presence of a loop in the linked list. The algorithm will then terminate and returntrue.
By following this method, the algorithm can efficiently determine whether a loop exists in the linked list.
Dry Run
When linked list length is odd
When linked list length is even
Solution
#include <iostream>
// Definition of singly linked list
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(NULL) {}
ListNode(int data1) : val(data1), next(NULL) {}
ListNode(int data1, ListNode *next1) : val(data1), next(next1) {}
};
class Solution {
public:
// Function to detect a loop in a linked
// list using the Tortoise and Hare Algorithm
bool hasCycle(ListNode *head) {
// Initialize two pointers, slow and fast,
// to the head of the linked list
ListNode *slow = head;
ListNode *fast = head;
// Step 2: Traverse the linked list with
// the slow and fast pointers
while (fast != nullptr && fast->next != nullptr) {
// Move slow one step
slow = slow->next;
// Move fast two steps
fast = fast->next->next;
// Check if slow and fast pointers meet
if (slow == fast) {
return true; // Loop detected
}
}
// If fast reaches the end of the list,
// there is no loop
return false;
}
};
// Main function to test the Solution
int main() {
// Create a sample linked list
// with a loop for testing
ListNode *head = new ListNode(1);
ListNode *second = new ListNode(2);
ListNode *third = new ListNode(3);
ListNode *fourth = new ListNode(4);
ListNode *fifth = new ListNode(5);
head->next = second;
second->next = third;
third->next = fourth;
fourth->next = fifth;
// Create a loop
fifth->next = third;
// Create an instance of the Solution class
Solution solution;
// Check if there is a loop
// in the linked list
if (solution.hasCycle(head)) {
std::cout << "Loop detected in the linked list." << std::endl;
} else {
std::cout << "No loop detected in the linked list." << std::endl;
}
// Clean up memory (free the allocated nodes)
delete head;
delete second;
delete third;
delete fourth;
delete fifth;
return 0;
}
import java.util.HashMap;
//Definition of singly linked list:
class ListNode {
int val;
ListNode next;
ListNode() {
val = 0;
next = null;
}
ListNode(int data1) {
val = data1;
next = null;
}
ListNode(int data1, ListNode next1) {
val = data1;
next = next1;
}
}
class Solution {
// Function to detect a loop in a linked
// list using the Tortoise and Hare Algorithm
public boolean hasCycle(ListNode head) {
// Initialize two pointers, slow and fast,
// to the head of the linked list
ListNode slow = head;
ListNode fast = head;
// Step 2: Traverse the linked list with
// the slow and fast pointers
while (fast != null && fast.next != null) {
// Move slow one step
slow = slow.next;
// Move fast two steps
fast = fast.next.next;
// Check if slow and fast pointers meet
if (slow == fast) {
return true; // Loop detected
}
}
// If fast reaches the end of the list,
// there is no loop
return false;
}
// Main function to test the Solution
public static void main(String[] args) {
// Create a sample linked list
// with a loop for testing
ListNode head = new ListNode(1);
ListNode second = new ListNode(2);
ListNode third = new ListNode(3);
ListNode fourth = new ListNode(4);
ListNode fifth = new ListNode(5);
head.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
// Create a loop
fifth.next = third;
// Create an instance of the Solution class
Solution solution = new Solution();
// Check if there is a loop
// in the linked list
if (solution.hasCycle(head)) {
System.out.println("Loop detected in the linked list.");
} else {
System.out.println("No loop detected in the linked list.");
}
}
}
# Definition of singly linked list:
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
# Function to detect a loop in a linked
# list using the Tortoise and Hare Algorithm
def hasCycle(self, head):
# Initialize two pointers, slow and fast,
# to the head of the linked list
slow = head
fast = head
# Step 2: Traverse the linked list with
# the slow and fast pointers
while fast is not None and fast.next is not None:
# Move slow one step
slow = slow.next
# Move fast two steps
fast = fast.next.next
# Check if slow and fast pointers meet
if slow == fast:
return True # Loop detected
# If fast reaches the end of the list,
# there is no loop
return False
# Main function to test the Solution
def main():
# Create a sample linked list
# with a loop for testing
head = ListNode(1)
second = ListNode(2)
third = ListNode(3)
fourth = ListNode(4)
fifth = ListNode(5)
head.next = second
second.next = third
third.next = fourth
fourth.next = fifth
# Create a loop
fifth.next = third
# Create an instance of the Solution class
solution = Solution()
# Check if there is a loop
# in the linked list
if solution.hasCycle(head):
print("Loop detected in the linked list.")
else:
print("No loop detected in the linked list.")
# Call the main function to execute the test
if __name__ == "__main__":
main()
/* Definition of singly linked list:
class ListNode {
constructor(val = 0, next = null) {
this.val = val;
this.next = next;
}
}
*/
class Solution {
// Function to detect a loop in a linked
// list using the Tortoise and Hare Algorithm
hasCycle(head) {
// Initialize two pointers, slow and fast,
// to the head of the linked list
let slow = head;
let fast = head;
// Step 2: Traverse the linked list with
// the slow and fast pointers
while (fast !== null && fast.next !== null) {
// Move slow one step
slow = slow.next;
// Move fast two steps
fast = fast.next.next;
// Check if slow and fast pointers meet
if (slow === fast) {
return true; // Loop detected
}
}
// If fast reaches the end of the list,
// there is no loop
return false;
}
}
// Main function to test the Solution
function main() {
// Create a sample linked list
// with a loop for testing
let head = new ListNode(1);
let second = new ListNode(2);
let third = new ListNode(3);
let fourth = new ListNode(4);
let fifth = new ListNode(5);
head.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
// Create a loop
fifth.next = third;
// Create an instance of the Solution class
let solution = new Solution();
// Check if there is a loop
// in the linked list
if (solution.hasCycle(head)) {
console.log("Loop detected in the linked list.");
} else {
console.log("No loop detected in the linked list.");
}
}
// Call the main function to execute the test
main();
Time Complexity: O(N), where N represents the number of nodes in the linked list. In the worst-case scenario, the fast pointer, which advances more quickly, will either reach the end of the list (if there's no loop) or catch up to the slow pointer (if there's a loop) in a time proportional to the length of the list.
The reason this complexity is O(N) and not slower is due to the fact that each step of the algorithm decreases the gap between the fast and slow pointers (when they are within the loop) by one node. Thus, the maximum number of steps required for them to meet is directly related to the number of nodes in the list.
Space Complexity: O(1) The algorithm utilizes a constant amount of additional space, regardless of the size of the linked list. This efficiency is achieved by using only two pointers (slow and fast) to detect the loop, without needing any significant extra memory, resulting in a constant space complexity of O(1).
Frequently Occurring Doubts
Q: Why does the fast pointer eventually catch up if a cycle exists?
A: The fast pointer moves twice as fast, so: If slow moves x steps, fast moves 2x steps. This guarantees that fast will eventually lap slow inside the cycle.
Q: Can we detect where the cycle begins (pos)?
A: Yes! After detecting the cycle, reset slow to head and move both slow and fast one step at a time. The node where they meet again is the cycle’s start node.
Interview Followup Questions
Q: How would you modify this to return the node where the cycle begins?
A: Use two-pointer reset technique: After detection, reset slow to head and move both pointers one step at a time. The first meeting point is the start of the cycle.
Q: What if we wanted to remove the cycle instead of just detecting it?
A: After finding the cycle start node, traverse the cycle to find the last node (tail). Set tail.next = NULL to break the cycle.
Notes
Code
true
false
true