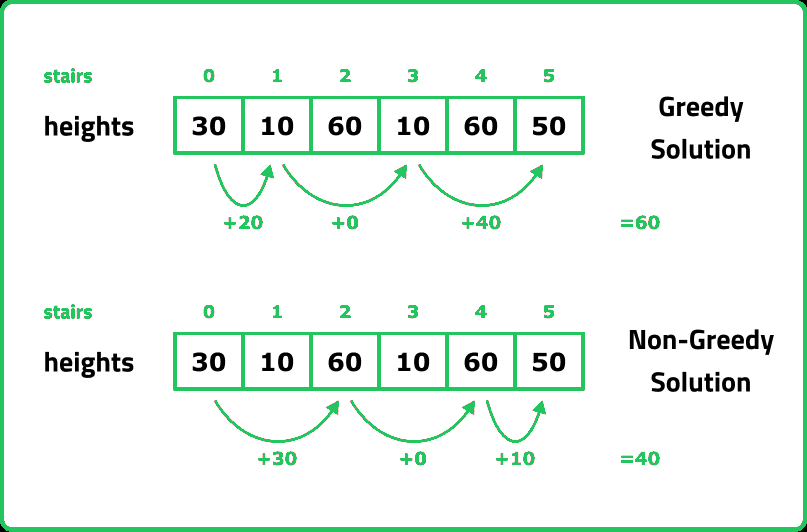
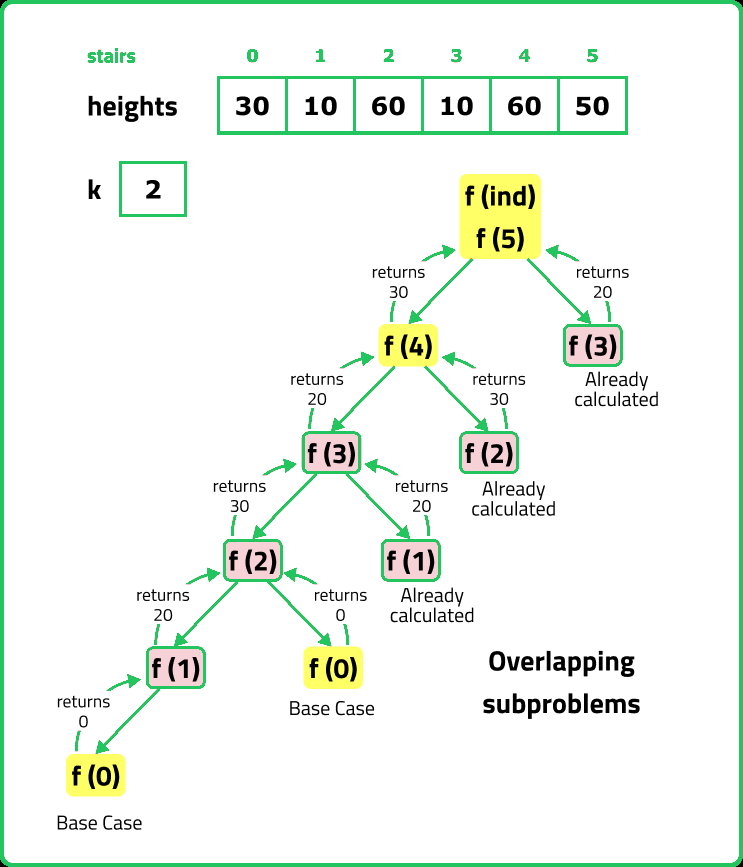
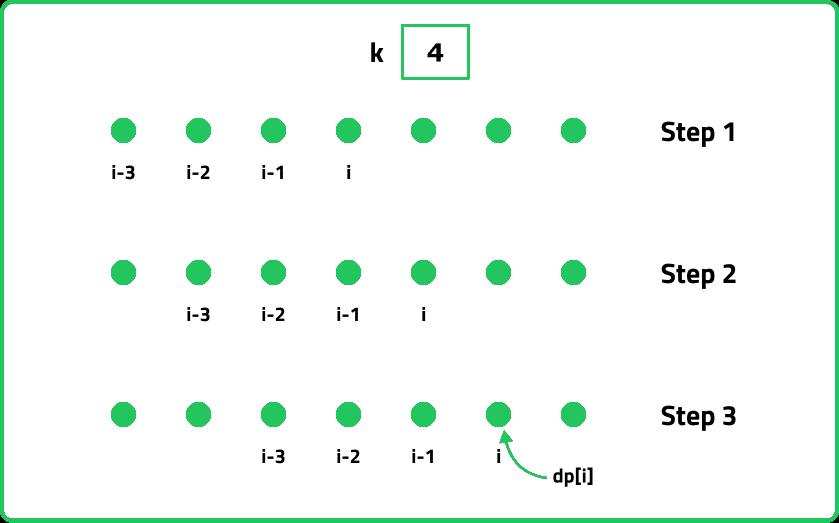
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to recursion with memoization
int func(int ind, vector<int> &heights, int k, vector<int>& dp){
//Base case
if(ind == 0){
return 0;
}
/* If the result for this index has
been previously calculated, return it */
if (dp[ind] != -1) return dp[ind];
//Initialize mmStep to INT_MAX
int mmStep = INT_MAX;
//Try all possible steps
for(int j = 1; j <= k; j++){
//Check if ind-j is non negative
if(ind-j >= 0){
int jump = func(ind-j, heights, k, dp) + abs(heights[ind] - heights[ind-j]);
//Update the mimimum energy
mmStep = min(jump, mmStep);
}
}
//Return the answer
return dp[ind] = mmStep;
}
public:
/* Function to find the mimimum
energy to reach last stair*/
int frogJump(vector<int> &heights, int k) {
int ind = heights.size()-1;
/*Initialize a memoization array
to store calculated results*/
vector<int> dp(ind+1, -1);
//Return the mimimum energy
return func(ind, heights, k, dp);
}
};
int main() {
vector<int> height{15, 4, 1, 14, 15};
int k = 3;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "Minimum energy : " << sol.frogJump(height, k) << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162
import java.util.*;
class Solution {
// Helper function for recursion with memoization
private int func(int ind, int[] heights, int k, int[] dp) {
// Base case
if (ind == 0) {
return 0;
}
/* If the result for this index has been
previously calculated, return it*/
if (dp[ind] != -1) {
return dp[ind];
}
// Initialize mmStep to Integer.MAX_VALUE
int mmStep = Integer.MAX_VALUE;
// Try all possible jumps
for (int j = 1; j <= k; j++) {
// Check if ind - j is non-negative
if (ind - j >= 0) {
int jump = func(ind - j, heights, k, dp) + Math.abs(heights[ind] - heights[ind - j]);
//Update the minimum energy
mmStep = Math.min(jump, mmStep);
}
}
// Store the result in dp array and return
dp[ind] = mmStep;
return dp[ind];
}
/* Function to find the minimum
energy to reach the last stair*/
public int frogJump(int[] heights, int k) {
int ind = heights.length - 1;
/* Initialize a memoization array
to store calculated results*/
int[] dp = new int[ind + 1];
Arrays.fill(dp, -1);
// Return the minimum energy
return func(ind, heights, k, dp);
}
public static void main(String[] args) {
int[] heights = {15, 4, 1, 14, 15};
int k = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the answer
System.out.println("Minimum energy: " + sol.frogJump(heights, k));
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
class Solution:
#Function for recusion using memoization
def func(self, ind, heights, k, dp):
# Base case
if ind == 0:
return 0
""" If the result for this index has been
previously calculated, return it"""
if dp[ind] != -1:
return dp[ind]
# Initialize mmStep to float('inf')
mmStep = float('inf')
# Try all possible jumps
for j in range(1, k + 1):
# Check if ind - j is non-negative
if ind - j >= 0:
jump = self.func(ind - j, heights, k, dp) + abs(heights[ind] - heights[ind - j])
#Update the minimum energy
mmStep = min(mmStep, jump)
# Store the result in dp array and return
dp[ind] = mmStep
return dp[ind]
def frogJump(self, heights, k):
ind = len(heights) - 1
""" Initialize a memoization array
to store calculated results"""
dp = [-1] * (ind + 1)
# Return the minimum energy
return self.func(ind, heights, k, dp)
if __name__ == "__main__":
heights = [15, 4, 1, 14, 15]
k = 3
# Create an instance of Solution class
sol = Solution()
# Print the answer
print("Minimum energy:", sol.frogJump(heights, k))
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
class Solution {
// Helper function for recursion with memoization
func(ind, heights, k, dp) {
// Base case
if (ind === 0) {
return 0;
}
/* If the result for this index has been
previously calculated, return it*/
if (dp[ind] !== -1) {
return dp[ind];
}
// Initialize mmStep to Infinity
let mmStep = Infinity;
// Try all possible jumps
for (let j = 1; j <= k; j++) {
// Check if ind - j is non-negative
if (ind - j >= 0) {
let jump = this.func(ind - j, heights, k, dp) + Math.abs(heights[ind] - heights[ind - j]);
//Update the minimum energy
mmStep = Math.min(jump, mmStep);
}
}
// Store the result in dp array and return
dp[ind] = mmStep;
return dp[ind];
}
/* Function to find the minimum
energy to reach the last stair*/
frogJump(heights, k) {
let ind = heights.length - 1;
/* Initialize a memoization array
to store calculated results*/
let dp = new Array(ind + 1).fill(-1);
// Return the minimum energy
return this.func(ind, heights, k, dp);
}
}
let heights = [15, 4, 1, 14, 15];
let k = 3;
// Create an instance of Solution class
let sol = new Solution();
// Print the answer
console.log("Minimum energy:", sol.frogJump(heights, k));