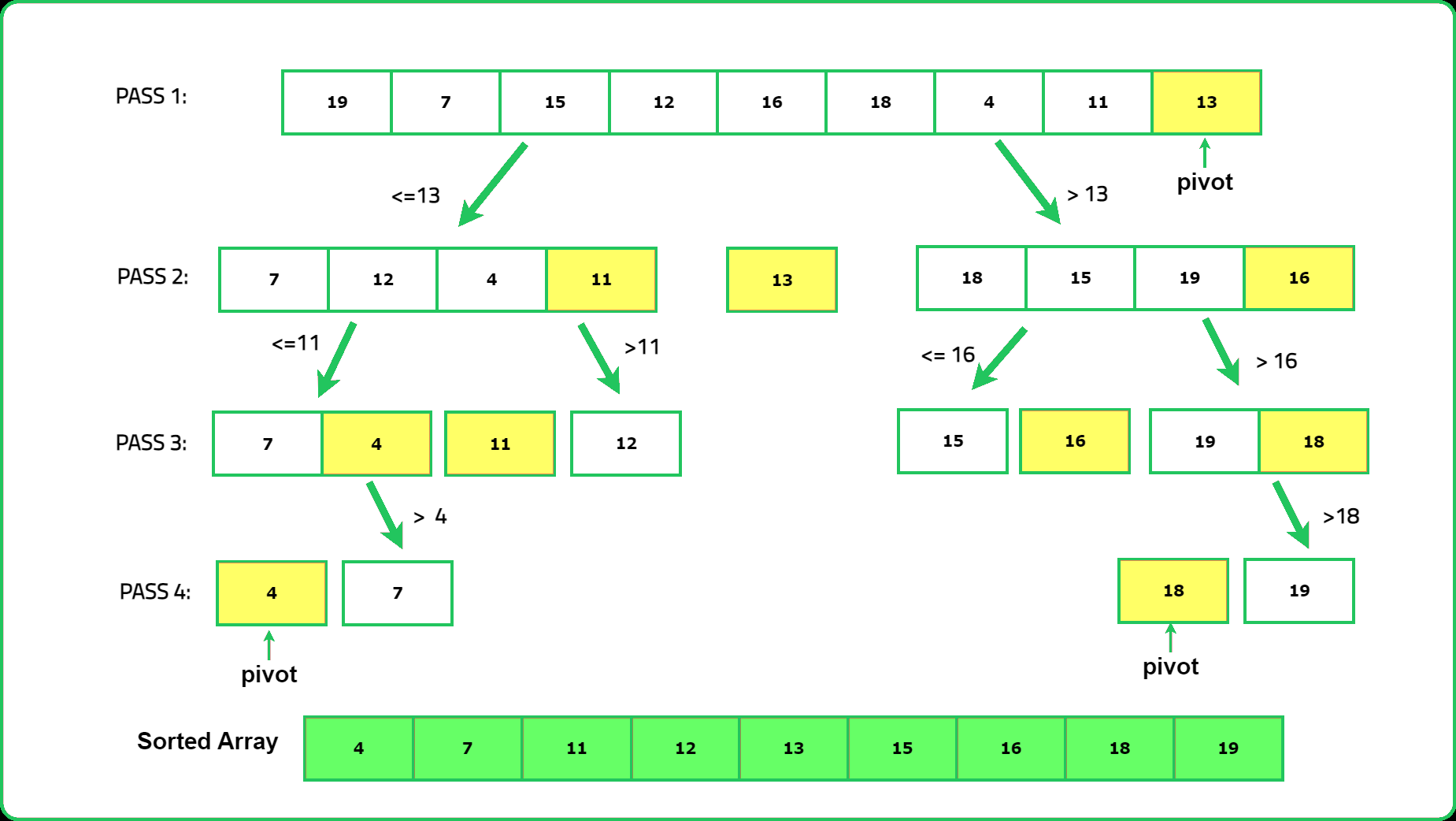
Quick Sorting
Sorting
Algorithms
Easy
- Fun Fact: Quick Sort algorithm, which is at the heart of this problem, is a widely used sorting algorithm in practical software development
- It is often used in file and database systems due to its efficient runtime performance
- For example, the Unix system command 'sort', used for arranging lines of text files or concatenating, is implemented using Quick Sort
- It's not only fast, but the algorithm also efficiently sorts in-place, meaning it doesn't require additional memory space to store sorted elements, unlike some other sorting algorithms
Given an array of integers called nums, sort the array in non-decreasing order using the quick sort algorithm and return the sorted array.
A sorted array in non-decreasing order is an array where each element is greater than or equal to all preceding elements in the array.
Examples:
Input: nums = [7, 4, 1, 5, 3]
Output: [1, 3, 4, 5, 7]
Explanation: 1 <= 3 <= 4 <= 5 <= 7.
Thus the array is sorted in non-decreasing order.
Input: nums = [5, 4, 4, 1, 1]
Output: [1, 1, 4, 4, 5]
Explanation: 1 <= 1 <= 4 <= 4 <= 5.
Thus the array is sorted in non-decreasing order.
Input: nums = [3, 2, 3, 4, 5]
Constraints
- 1 <= nums.length <= 105
- -104 <= nums[i] <= 104
- nums[i] may contain duplicate values.
Hints
- Focus on choosing a pivot element. All elements smaller than the pivot go to its left, and all larger elements go to its right. Think about recursively applying the same partitioning logic to the left and right subarrays created by the pivot.
- Consider how swapping elements helps to ensure that the pivot ends up in its correct position after partitioning.
Company Tags
Medtronic
Ubisoft
Riot Games
Mastercard
Byju's
Splunk
Morgan Stanley
Electronic Arts
Bloomberg
Salesforce
Epic Games
Robinhood
Ernst & Young
Roche
IBM
Docker
Siemens Healthineers
Rockstar Games
McKinsey & Company
Johnson & Johnson
Boston Consulting Group
Pinterest
Rakuten
Activision Blizzard
Intel
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro