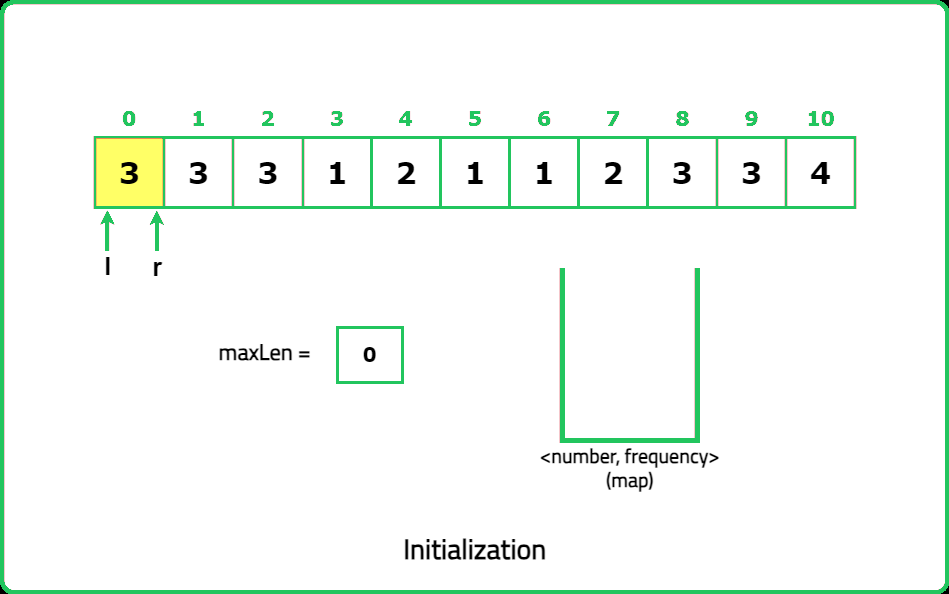
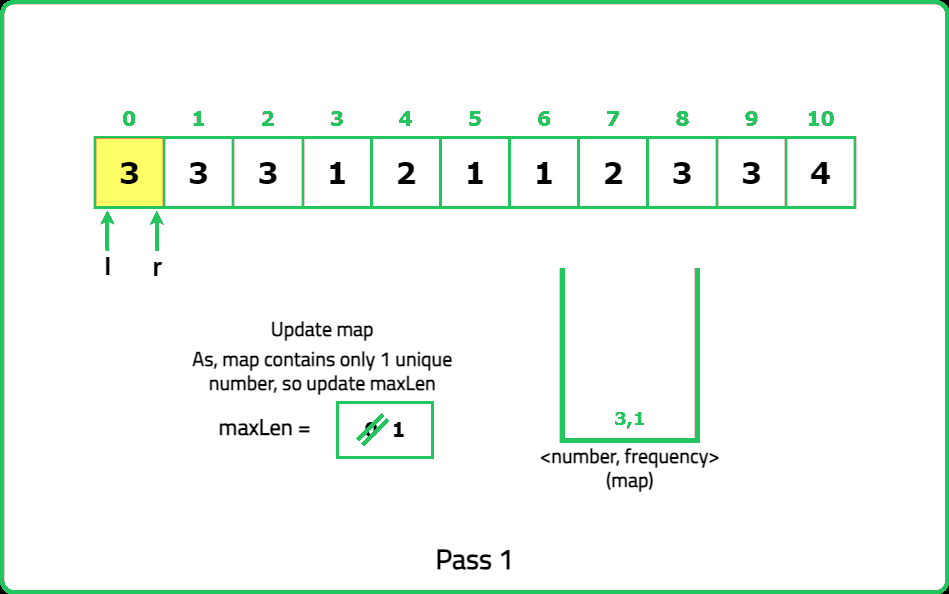
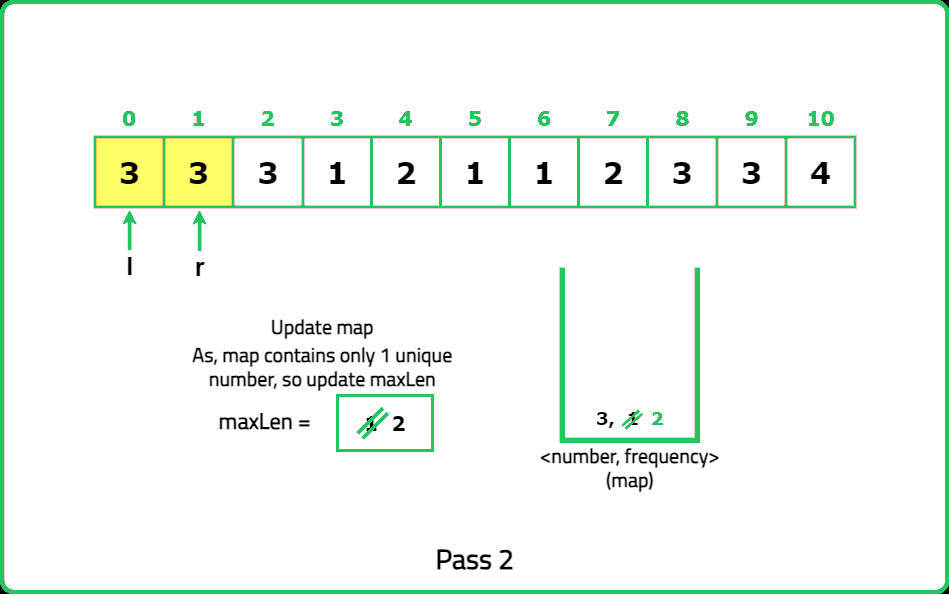
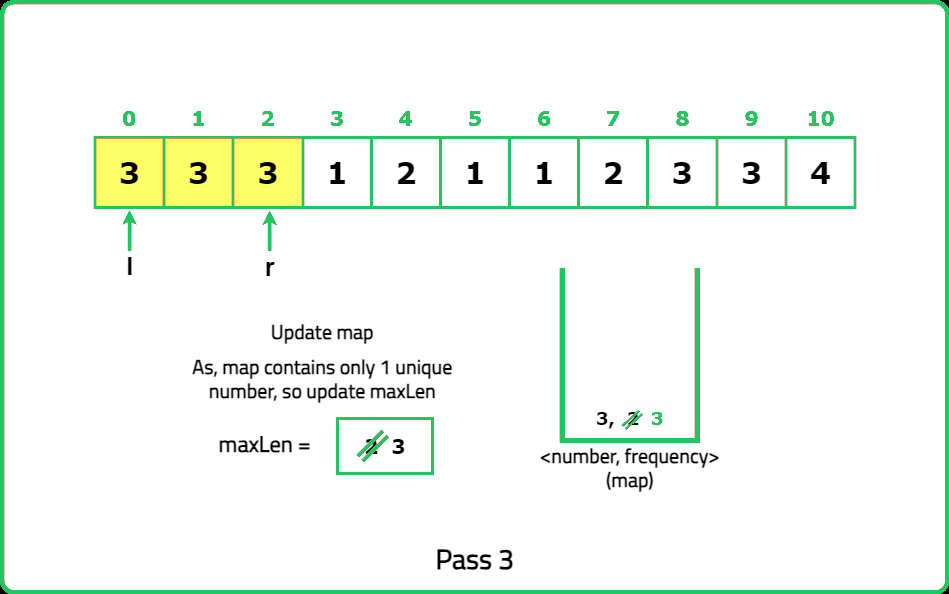
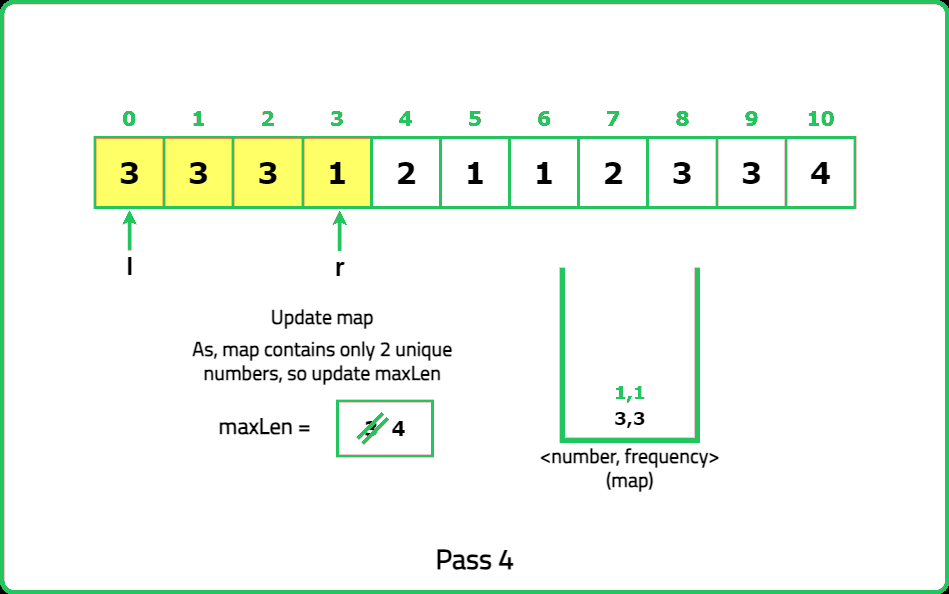
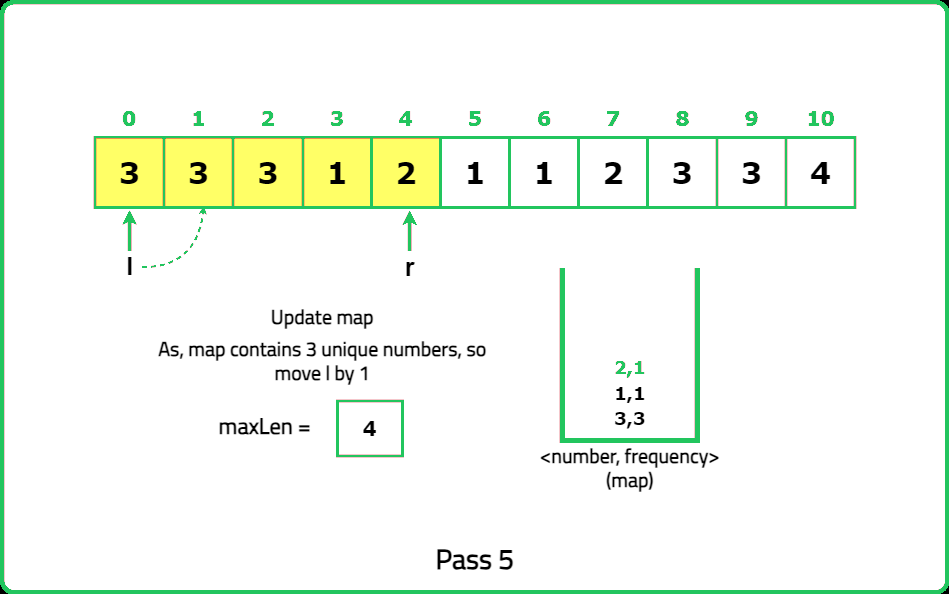
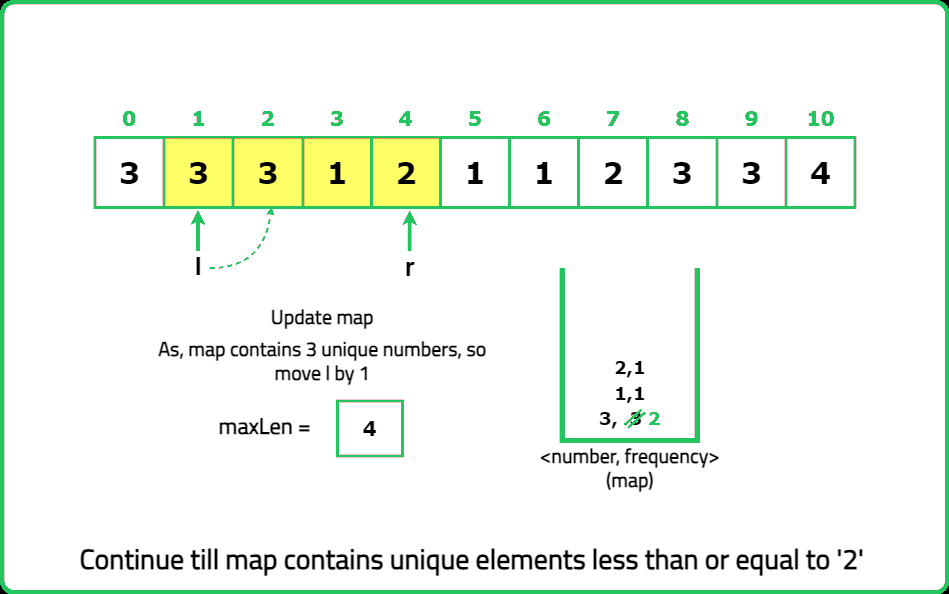
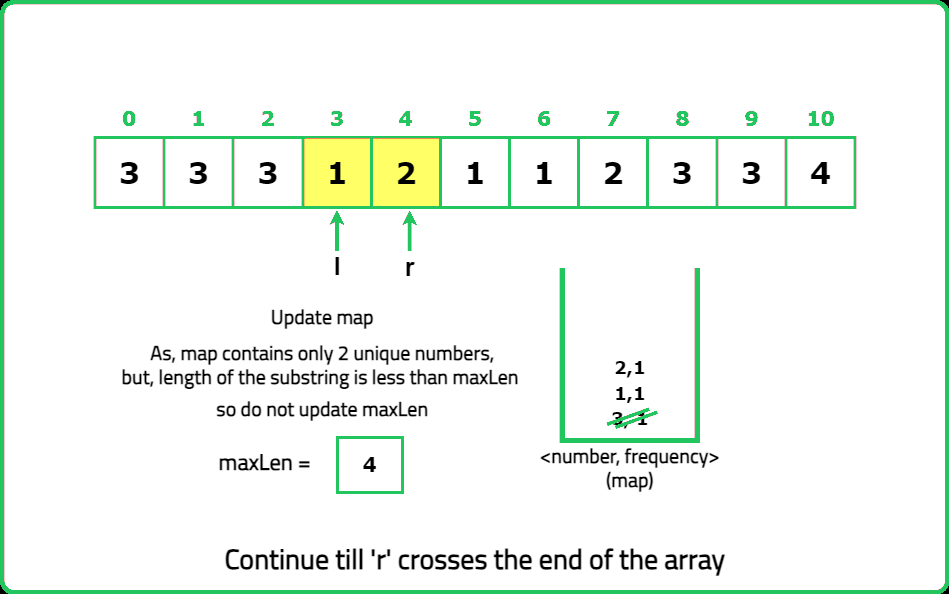
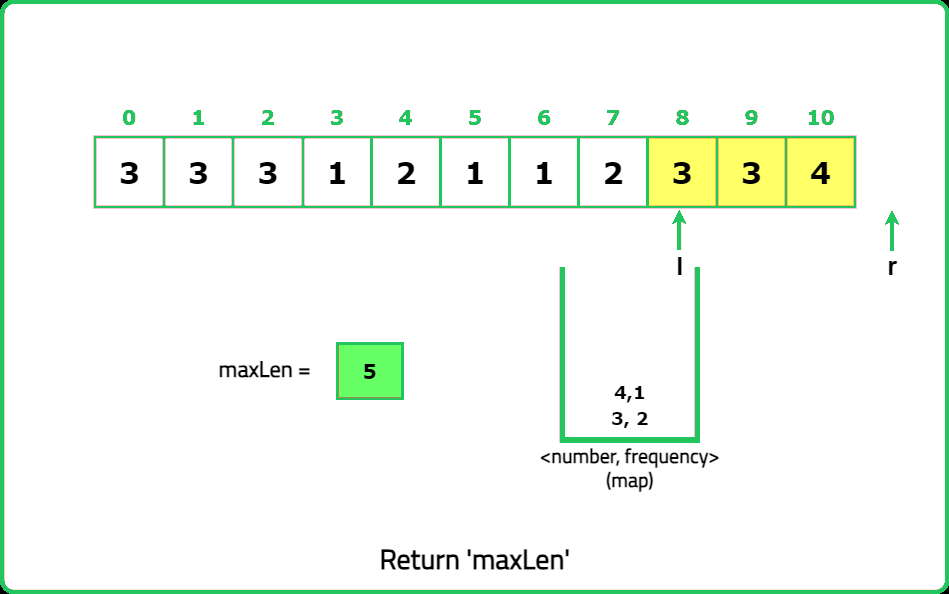
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Function to find the maximum
fruits the basket can have */
int totalFruits(vector<int>& fruits) {
// Length of the input array
int n = fruits.size();
/* Variable to store the
maximum length of substring*/
int maxLen = 0;
/* Map to track the count of each
fruit type in the current window*/
unordered_map<int, int> mpp;
// Pointers for the sliding window approach
int l = 0, r = 0;
while(r < n){
mpp[fruits[r]]++;
/* If number of different fruits exceeds
2 shrink the window from the left*/
if(mpp.size() > 2){
while(mpp.size() > 2){
mpp[fruits[l]]--;
if(mpp[fruits[l]] == 0){
mpp.erase(fruits[l]);
}
l++;
}
}
/* If number of different fruits
is at most 2, update maxLen*/
if(mpp.size() <= 2){
maxLen = max(maxLen, r - l + 1);
}
r++;
}
// Return the maximum fruit
return maxLen;
}
};
int main() {
vector<int> input = {3, 3, 3, 1, 2, 1, 1, 2, 3, 3, 4};
// Create an instance of Solution class
Solution sol;
int length = sol.totalFruits(input);
// Print the result
cout << "Maximum fruits the can have is: " << length << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162
import java.util.*;
class Solution {
/* Function to find the maximum
fruits the basket can have */
public int totalFruits(int[] fruits) {
// Length of the input array
int n = fruits.length;
/* Variable to store the
maximum length of substring */
int maxLen = 0;
/* Map to track the count of each
fruit type in the current window */
HashMap<Integer, Integer> mpp = new HashMap<>();
// Pointers for the sliding window approach
int l = 0, r = 0;
while (r < n) {
mpp.put(fruits[r], mpp.getOrDefault(fruits[r], 0) + 1);
/* If number of different fruits exceeds
2 shrink the window from the left */
if (mpp.size() > 2) {
while (mpp.size() > 2) {
mpp.put(fruits[l], mpp.get(fruits[l]) - 1);
if (mpp.get(fruits[l]) == 0) {
mpp.remove(fruits[l]);
}
l++;
}
}
/* If number of different fruits
is at most 2, update maxLen */
if (mpp.size() <= 2) {
maxLen = Math.max(maxLen, r - l + 1);
}
r++;
}
// Return the maximum fruit
return maxLen;
}
public static void main(String[] args) {
int[] input = {3, 3, 3, 1, 2, 1, 1, 2, 3, 3, 4};
// Create an instance of Solution class
Solution sol = new Solution();
int length = sol.totalFruits(input);
// Print the result
System.out.println("Maximum fruits the basket can have: " + length);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
class Solution:
""" Function to find the maximum
fruits the basket can have """
def totalFruits(self, fruits):
# Length of the input array
n = len(fruits)
""" Variable to store the
maximum length of substring """
maxLen = 0
""" Dictionary to track the count of each
fruit type in the current window """
mpp = {}
# Pointers for the sliding window approach
l, r = 0, 0
while r < n:
mpp[fruits[r]] = mpp.get(fruits[r], 0) + 1
""" If number of different fruits exceeds
2 shrink the window from the left """
if len(mpp) > 2:
while len(mpp) > 2:
mpp[fruits[l]] -= 1
if mpp[fruits[l]] == 0:
del mpp[fruits[l]]
l += 1
""" If number of different fruits
is at most 2, update maxLen """
if len(mpp) <= 2:
maxLen = max(maxLen, r - l + 1)
r += 1
# Return the maximum fruit
return maxLen
# Test the solution
if __name__ == "__main__":
input = [3, 3, 3, 1, 2, 1, 1, 2, 3, 3, 4]
# Create an instance of Solution class
sol = Solution()
length = sol.totalFruits(input)
# Print the result
print(f"Maximum fruits the basket can have: {length}")
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758
class Solution {
/* Function to find the maximum
fruits the basket can have */
totalFruits(fruits) {
// Length of the input array
let n = fruits.length;
/* Variable to store the
maximum length of substring */
let maxLen = 0;
/* Map to track the count of each
fruit type in the current window */
let mpp = new Map();
// Pointers for the sliding window approach
let l = 0, r = 0;
while (r < n) {
mpp.set(fruits[r], (mpp.get(fruits[r]) || 0) + 1);
/* If number of different fruits exceeds
2 shrink the window from the left */
if (mpp.size > 2) {
while (mpp.size > 2) {
mpp.set(fruits[l], mpp.get(fruits[l]) - 1);
if (mpp.get(fruits[l]) === 0) {
mpp.delete(fruits[l]);
}
l++;
}
}
/* If number of different fruits
is at most 2, update maxLen */
if (mpp.size <= 2) {
maxLen = Math.max(maxLen, r - l + 1);
}
r++;
}
// Return the maximum fruit
return maxLen;
}
}
let input = [3, 3, 3, 1, 2, 1, 1, 2, 3, 3, 4];
// Create an instance of Solution class
let sol = new Solution();
let len = sol.totalFruits(input);
// Print the result
console.log(`Maximum fruits the basket can have: ${len}`);