Print all primes till N
Maths
Sieve of Eratosthenes
Hard
You are given an integer n.
Print all the prime numbers till n (including n).
A prime number is a number that has only two divisor's 1 and the number itself.
Examples:
Input : n = 7
Output : [2, 3, 5, 7]
Explanation : The number 2 has only two divisors 1 and 2.
The number 3 has only two divisors 1 and 3.
The number 5 has only two divisors 1 and 5.
The number 7 has only two divisors 1 and 7.
Input : n = 2
Output : [2]
Explanation : There is only one number 2 that is a prime till 2.
Input : n = 10
Constraints
- 2 <= n <= 5*105
Hints
- A brute-force approach would check each number from 2 to n and determine if it is prime by checking divisibility from 2 to sqrt(n). However, this results in O(n√n) complexity, which is inefficient for large n.
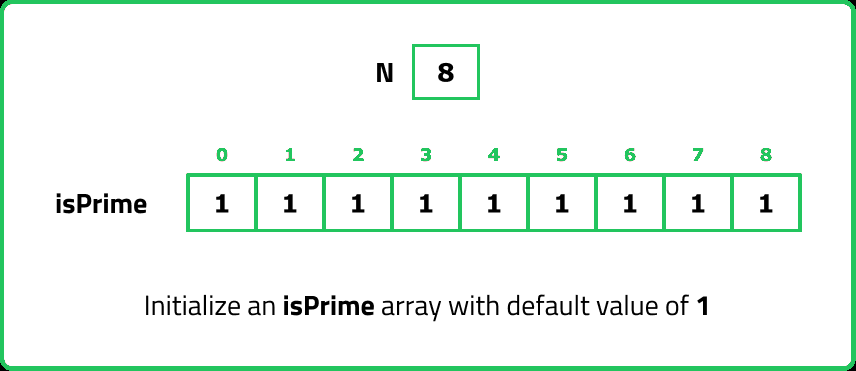
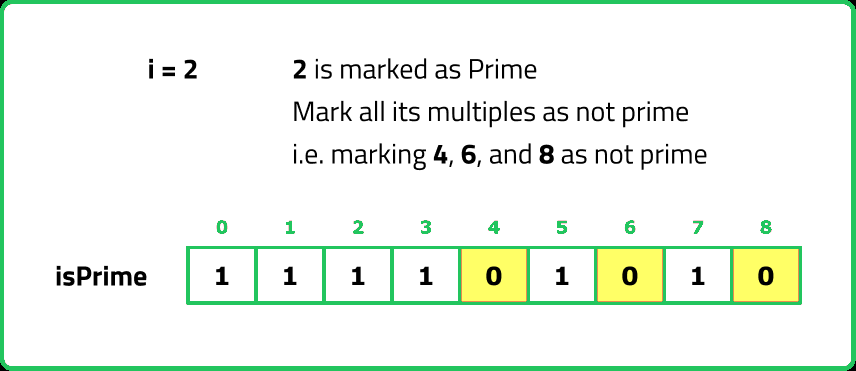
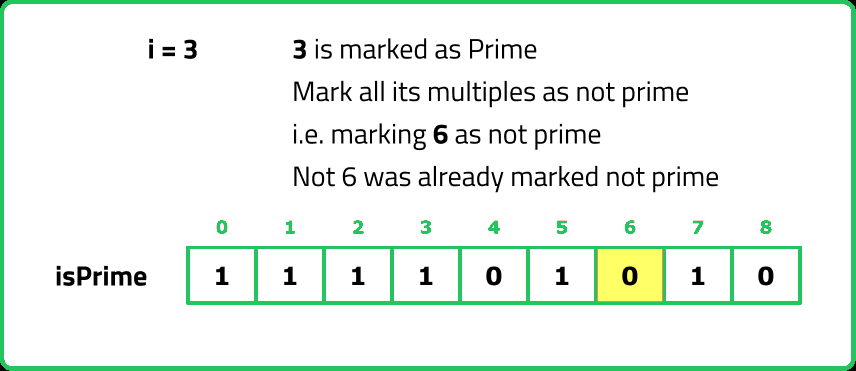
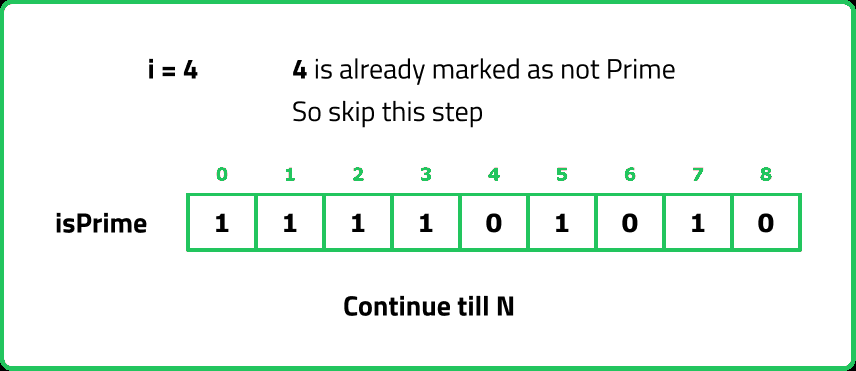
- "A more efficient approach is the Sieve of Eratosthenes, which: Assumes all numbers are prime initially. Iteratively marks multiples of known primes as non-prime. Outputs the remaining numbers as prime."
Company Tags
Roblox
Twilio
Rockstar Games
Reddit
Roche
Optum
Pinterest
Bain & Company
Medtronic
HCL Technologies
Alibaba
Deloitte
Epic Systems
Ubisoft
Wayfair
Bloomberg
Instacart
Mastercard
Robinhood
Philips Healthcare
ARM
GE Healthcare
McKinsey & Company
Rakuten
eBay
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe