Serialize and De-serialize BT

Binary Trees Construction Problems Hard

Did you know that the concept of serialization and deserialization is heavily used in sending and receiving data over the network or storing data in databases? For instance, in web development, when data is fetched from an API, it's often transmitted in JSON format which is text-based and easy to read
But, that's not how your objects exist in your code
They're in the form of complex data structures or binary format
Hence, they need to be converted (serialize) into a string form to travel across the network
Then, at the destination, they are converted back (deserialize) into usable objects
This allows different software systems, possibly deployed on different platforms and written in different languages, to communicate and exchange complex data

Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. Ensure that a binary tree can be serialized to a string, and this string can be deserialized to the original tree structure.

The encoded string should be as compact as possible.

Examples:

Input : root = [2, 1, 3]

Output : [2, 1, 3]

Input : root = [7, 3, 15, null, null, 9, 20]

Output : [7, 3, 15, null, null, 9, 20]

Input : root = [10, 20, 30, 40, 50, 60]

Constraints

1 <= Number of Nodes <= 10⁴
0 <= Node.val <= 10⁴

Hints

Serialization: Use BFS (level-order traversal) to process nodes. Store null values for missing children to maintain tree structure. Use comma-separated values (CSV format). Use Preorder traversal (Root → Left → Right). Store "N" (or null) for missing children.
Deserialization: Read the string and split it into nodes. Use a queue to rebuild the tree level by level. Read values sequentially and recursively reconstruct the tree.

Company Tags

Stripe Rockstar Games PayPal Databricks ARM HCL Technologies Robinhood Uber Intel Zomato HashiCorp MongoDB Epic Games Broadcom Walmart Activision Blizzard Bungie DoorDash Target McKinsey & Company Alibaba Cerner KPMG JPMorgan Chase American Express Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Serialisation

Intuition

The concept of serializing a binary tree involves transforming its structure into a string format that preserves the hierarchical arrangement of nodes. By utilizing level-order traversal (BFS), we can ensure that nodes are processed in the order of their levels, which simplifies the reconstruction of the tree during deserialization. In this approach, each node's value is recorded in the string, while null nodes are represented by a special placeholder (e.g., "#") to maintain the integrity of the tree structure.

Approach

First, check if the tree is empty. If the root is null, return an empty string. Otherwise, initialize an empty string to hold the serialized data of the binary tree.
Utilize a queue for level-order traversal. Begin by initializing a queue and enqueueing the root node.
In the level-order traversal process: Dequeue a node from the queue. If the node is null, append "#" to the string. If the node is not null, append its value followed by a comma (",") to the string and enqueue its left and right children.
Continue this process until the queue is empty, and then return the final string which contains the complete serialized representation of the binary tree.

Dry run

Deserialization

Intuition

Deserialization involves reconstructing a binary tree from its serialized string representation. The process relies on level-order traversal (BFS) to read the nodes in the sequence they appear in the serialized data, facilitating accurate tree reconstruction. Each node's value is extracted from the string, with null nodes represented by a specific character (e.g., "#") to denote the absence of a child node.

Approach

Start by checking if the serialized string is empty. If it is, return null as there is no tree to reconstruct.
Split the serialized string into individual node values using a comma delimiter. The first value represents the root of the tree, which should be used to create the root node. Initialize a queue and enqueue the root node to facilitate level-order construction.
Perform level-order traversal: Dequeue a node from the queue. Read the next value from the tokenized data to determine the left child. If this value is "#", set the left child to null; otherwise, create a new node. Repeat the process for the right child. If the right child’s value is "#", set it to null; otherwise, create a new node. Enqueue both left and right children for further processing.
Continue the traversal until all nodes are processed and the queue is empty. Finally, return the root node of the fully reconstructed binary tree.

Dry run

Solution

#include <bits/stdc++.h>
using namespace std;

// Definition for a binary tree node.
  struct TreeNode {
      int data;
      TreeNode *left;
      TreeNode *right;
       TreeNode(int val) : data(val) , left(nullptr) , right(nullptr) {}
  };
 

class Solution {
public:
    // Encodes the tree into a single string
    string serialize(TreeNode* root) {
        if (root == nullptr) {
            return "";
        }

        // Initialize an empty string
        // to store the serialized data
        stringstream ss;
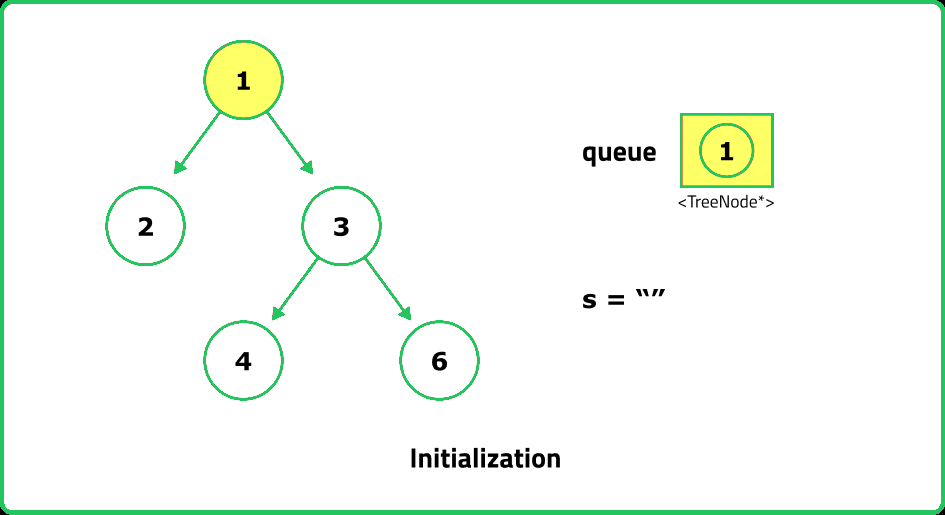
        // Use a queue for level-order traversal
        queue<TreeNode*> q;
        // Start with the root node
        q.push(root);

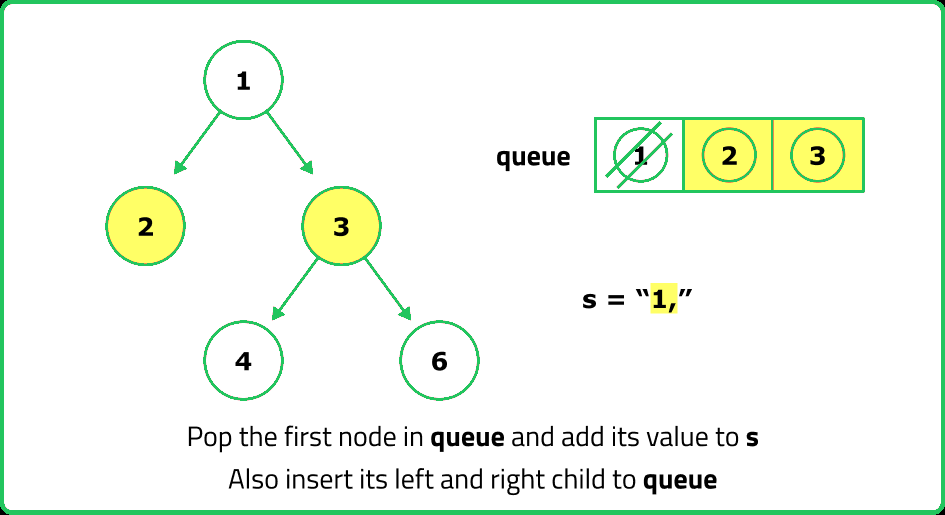
        // Perform level-order traversal
        while (!q.empty()) {
            // Get the front node in the queue
            TreeNode* curNode = q.front();
            q.pop();

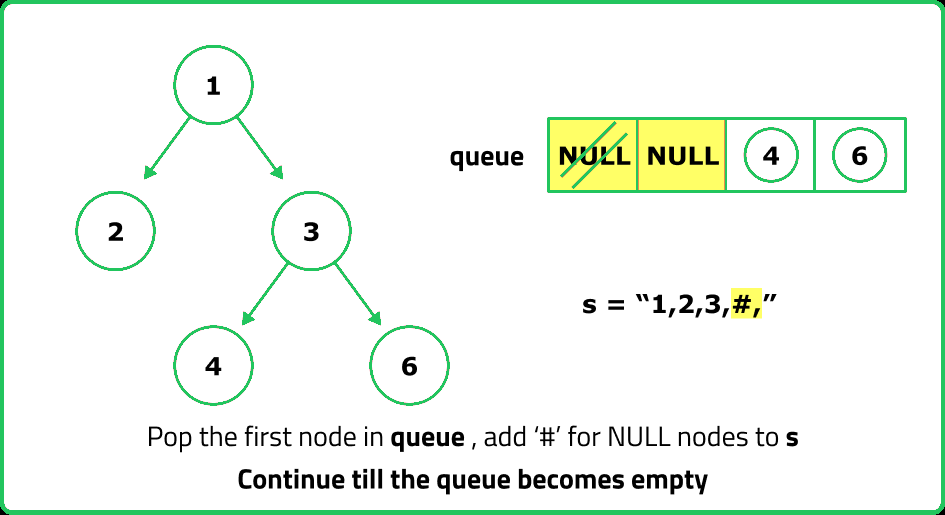
            // Check if the current node is null and append "#" to the string
            if (curNode == nullptr) {
                ss << "#,";
            } else {
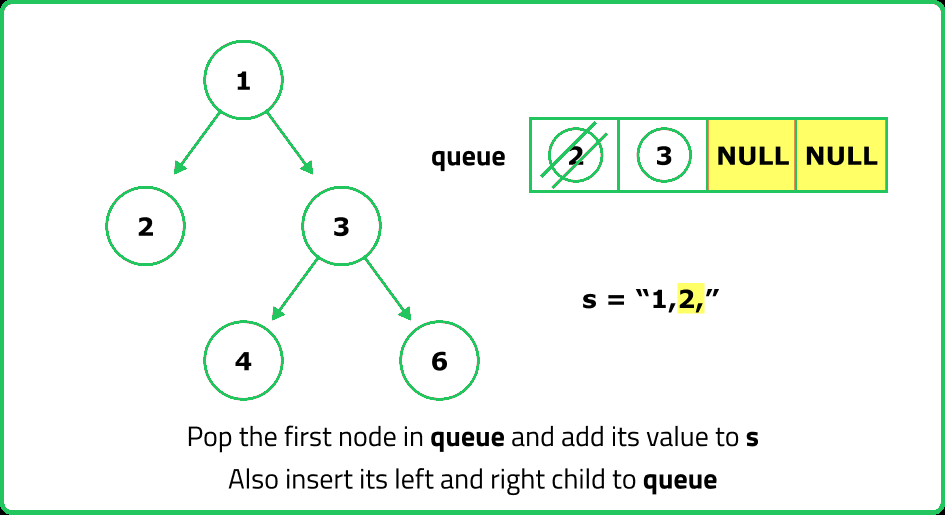
                // Append the value of the current node to the string
                ss << curNode->data << ",";
                // Push the left and right children to the queue for further traversal
                q.push(curNode->left);
                q.push(curNode->right);
            }
        }

        // Return the serialized string
        return ss.str();
    }

    // Decode the encoded data to a tree
    TreeNode* deserialize(string data) {
        if (data.empty()) {
            return nullptr;
        }

        // Use a stringstream to tokenize the serialized data
        stringstream s(data);
        string str;
        getline(s, str, ',');
        // Read the root value from the serialized data
        TreeNode* root = new TreeNode(stoi(str));

        // Use a queue for level-order traversal
        queue<TreeNode*> q;
        // Start with the root node
        q.push(root);

        // Perform level-order traversal to reconstruct the tree
        while (!q.empty()) {
            TreeNode* node = q.front();
            q.pop();

            // Read the value of the left child from the serialized data
            getline(s, str, ',');
            if (str != "#") {
                TreeNode* leftNode = new TreeNode(stoi(str));
                node->left = leftNode;
                q.push(leftNode);
            }

            // Read the value of the right child from the serialized data
            getline(s, str, ',');
            if (str != "#") {
                TreeNode* rightNode = new TreeNode(stoi(str));
                node->right = rightNode;
                q.push(rightNode);
            }
        }

        // Return the reconstructed root of the tree
        return root;
    }

    static void inorder(TreeNode* root) {
        if (root == nullptr) {
            return;
        }
        inorder(root->left);
        cout << root->data << " ";
        inorder(root->right);
    }
};

int main() {
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->right->left = new TreeNode(4);
    root->right->right = new TreeNode(5);

    Solution solution;
    cout << "Original Tree: ";
    Solution::inorder(root);
    cout << endl;

    string serialized = solution.serialize(root);
    cout << "Serialized: " << serialized << endl;

    TreeNode* deserialized = solution.deserialize(serialized);
    cout << "Tree after deserialization: ";
    Solution::inorder(deserialized);
    cout << endl;

    return 0;
}
import java.util.LinkedList;
import java.util.Queue;

 // Definition for a binary tree node.
public  class TreeNode {
      int data;
      TreeNode left;
      TreeNode right;
      TreeNode(int val) { data = val; left = null, right = null }
  }
 

class Solution {

    // Encodes the tree into a single string
    public String serialize(TreeNode root) {
        if (root == null) {
            return "";
        }

        // Initialize an empty string to store the serialized data
        StringBuilder sb = new StringBuilder();
        // Use a queue for level-order traversal
        Queue<TreeNode> q = new LinkedList<>();
        // Start with the root node
        q.offer(root);

        // Perform level-order traversal
        while (!q.isEmpty()) {
            TreeNode curNode = q.poll();

            // Check if the current node is null and append "#" to the string
            if (curNode == null) {
                sb.append("#,");
            } else {
                // Append the value of the current node to the string
                sb.append(curNode.data).append(",");
                // Push the left and right children to the queue for further traversal
                q.offer(curNode.left);
                q.offer(curNode.right);
            }
        }

        // Return the serialized string
        return sb.toString();
    }

    // Decode the encoded data to a tree
    public TreeNode deserialize(String data) {
        if (data.isEmpty()) {
            return null;
        }

        // Use a StringBuilder to tokenize the serialized data
        StringBuilder s = new StringBuilder(data);
        String str;
        int commaIndex = s.indexOf(",");
        str = s.substring(0, commaIndex);
        s.delete(0, commaIndex + 1);
        // Read the root value from the serialized data
        TreeNode root = new TreeNode(Integer.parseInt(str));

        // Use a queue for level-order traversal
        Queue<TreeNode> q = new LinkedList<>();
        // Start with the root node
        q.offer(root);

        // Perform level-order traversal to reconstruct the tree
        while (!q.isEmpty()) {
            TreeNode node = q.poll();

            // Read the value of the left child from the serialized data
            commaIndex = s.indexOf(",");
            str = s.substring(0, commaIndex);
            s.delete(0, commaIndex + 1);
            if (!str.equals("#")) {
                TreeNode leftNode = new TreeNode(Integer.parseInt(str));
                node.left = leftNode;
                q.offer(leftNode);
            }

            // Read the value of the right child from the serialized data
            commaIndex = s.indexOf(",");
            str = s.substring(0, commaIndex);
            s.delete(0, commaIndex + 1);
            if (!str.equals("#")) {
                TreeNode rightNode = new TreeNode(Integer.parseInt(str));
                node.right = rightNode;
                q.offer(rightNode);
            }
        }

        // Return the reconstructed root of the tree
        return root;
    }

    public static void inorder(TreeNode root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        System.out.print(root.data + " ");
        inorder(root.right);
    }

    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.right.left = new TreeNode(4);
        root.right.right = new TreeNode(5);

        Solution solution = new Solution();
        System.out.print("Original Tree: ");
        inorder(root);
        System.out.println();

        String serialized = solution.serialize(root);
        System.out.println("Serialized: " + serialized);

        TreeNode deserialized = solution.deserialize(serialized);
        System.out.print("Tree after deserialization: ");
        inorder(deserialized);
        System.out.println();
    }
}
from collections import deque

# Definition for a binary tree node.
 class TreeNode(object):
     def __init__(self, val=0, left=None, right=None):
         self.data = val
         self.left = left
         self.right = right

class Solution:
    def serialize(self, root):
        """
        Encodes the tree into a single string.
        :type root: TreeNode
        :rtype: str
        """
        if not root:
            return ""

        # Initialize an empty string to store the serialized data
        result = []
        # Use a queue for level-order traversal
        q = deque([root])

        # Perform level-order traversal
        while q:
            node = q.popleft()
            if node is None:
                result.append("#")
            else:
                result.append(str(node.data))
                # Push the left and right children to the queue for further traversal
                q.append(node.left)
                q.append(node.right)

        # Return the serialized string
        return ",".join(result)

    def deserialize(self, data):
        """
        Decodes the encoded data to a tree.
        :type data: str
        :rtype: TreeNode
        """
        if not data:
            return None

        # Use a deque to tokenize the serialized data
        data = deque(data.split(","))
        # Read the root value from the serialized data
        root = TreeNode(int(data.popleft()))

        # Use a queue for level-order traversal
        q = deque([root])

        # Perform level-order traversal to reconstruct the tree
        while q:
            node = q.popleft()

            # Read the value of the left child from the serialized data
            left_val = data.popleft()
            if left_val != "#":
                left_node = TreeNode(int(left_val))
                node.left = left_node
                q.append(left_node)

            # Read the value of the right child from the serialized data
            right_val = data.popleft()
            if right_val != "#":
                right_node = TreeNode(int(right_val))
                node.right = right_node
                q.append(right_node)

        # Return the reconstructed root of the tree
        return root

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# tree = ser.serialize(root)
# ans = deser.deserialize(tree)
# return ans

# Testing the Solution
if __name__ == "__main__":
    # Create the binary tree
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.right.left = TreeNode(4)
    root.right.right = TreeNode(5)

    solution = Solution()
    print("Original Tree: ", end="")
    def inorder(root):
        if root is None:
            return
        inorder(root.left)
        print(root.data, end=" ")
        inorder(root.right)
    inorder(root)
    print()

    serialized = solution.serialize(root)
    print("Serialized:", serialized)

    deserialized = solution.deserialize(serialized)
    print("Tree after deserialization: ", end="")
    inorder(deserialized)
    print()
// Definition for a binary tree node.
  class TreeNode {
       constructor(val = 0, left = null, right = null){
           this.data = val;
           this.left = left;
           this.right = right;
       }
  }
 
class Solution {
  // Encodes the tree into a single string
  serialize(root) {
    if (root === null) {
      return "";
    }

    // Initialize an empty string to store the serialized data
    let result = [];
    // Use a queue for level-order traversal
    let queue = [root];

    // Perform level-order traversal
    while (queue.length) {
      let node = queue.shift();
      if (node === null) {
        result.push("#");
      } else {
        result.push(node.data);
        // Push the left and right children to the queue for further traversal
        queue.push(node.left);
        queue.push(node.right);
      }
    }

    // Return the serialized string
    return result.join(",");
  }

  // Decode the encoded data to a tree
  deserialize(data) {
    if (data === "") {
      return null;
    }

    // Use a string tokenizer to extract node values
    let nodes = data.split(",");
    // Read the root value from the serialized data
    let root = new TreeNode(parseInt(nodes.shift()));

    // Use a queue for level-order traversal
    let queue = [root];

    // Perform level-order traversal to reconstruct the tree
    while (queue.length) {
      let node = queue.shift();

      // Read the value of the left child from the serialized data
      let leftVal = nodes.shift();
      if (leftVal !== "#") {
        let leftNode = new TreeNode(parseInt(leftVal));
        node.left = leftNode;
        queue.push(leftNode);
      }

      // Read the value of the right child from the serialized data
      let rightVal = nodes.shift();
      if (rightVal !== "#") {
        let rightNode = new TreeNode(parseInt(rightVal));
        node.right = rightNode;
        queue.push(rightNode);
      }
    }

    // Return the reconstructed root of the tree
    return root;
  }
}

// Testing the Solution
function inorder(root) {
  if (root === null) {
    return;
  }
  inorder(root.left);
  console.log(root.data + " ");
  inorder(root.right);
}

// Create the binary tree
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.right.left = new TreeNode(4);
root.right.right = new TreeNode(5);

let solution = new Solution();
console.log("Original Tree:");
inorder(root);

let serialized = solution.serialize(root);
console.log("Serialized:", serialized);

let deserialized = solution.deserialize(serialized);
console.log("Tree after deserialization:");
inorder(deserialized);

Complexity Analysis

Time Complexity: O(N) Both serialize and deserialize functions have a time complexity of O(N), where N is the number of nodes in the tree. This is because each function processes every node once.

Space Complexity: O(N) Both serialize and deserialize functions have a space complexity of O(N). This space is used by the queue to hold nodes at various levels of the tree during traversal and reconstruction.

Code

Problem List

Serialize and De-serialize BT

Examples:

Constraints

Hints

Company Tags

Editorial

Serialisation

Intuition

Approach

Dry run

Deserialization

Intuition

Approach

Dry run

Solution

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code