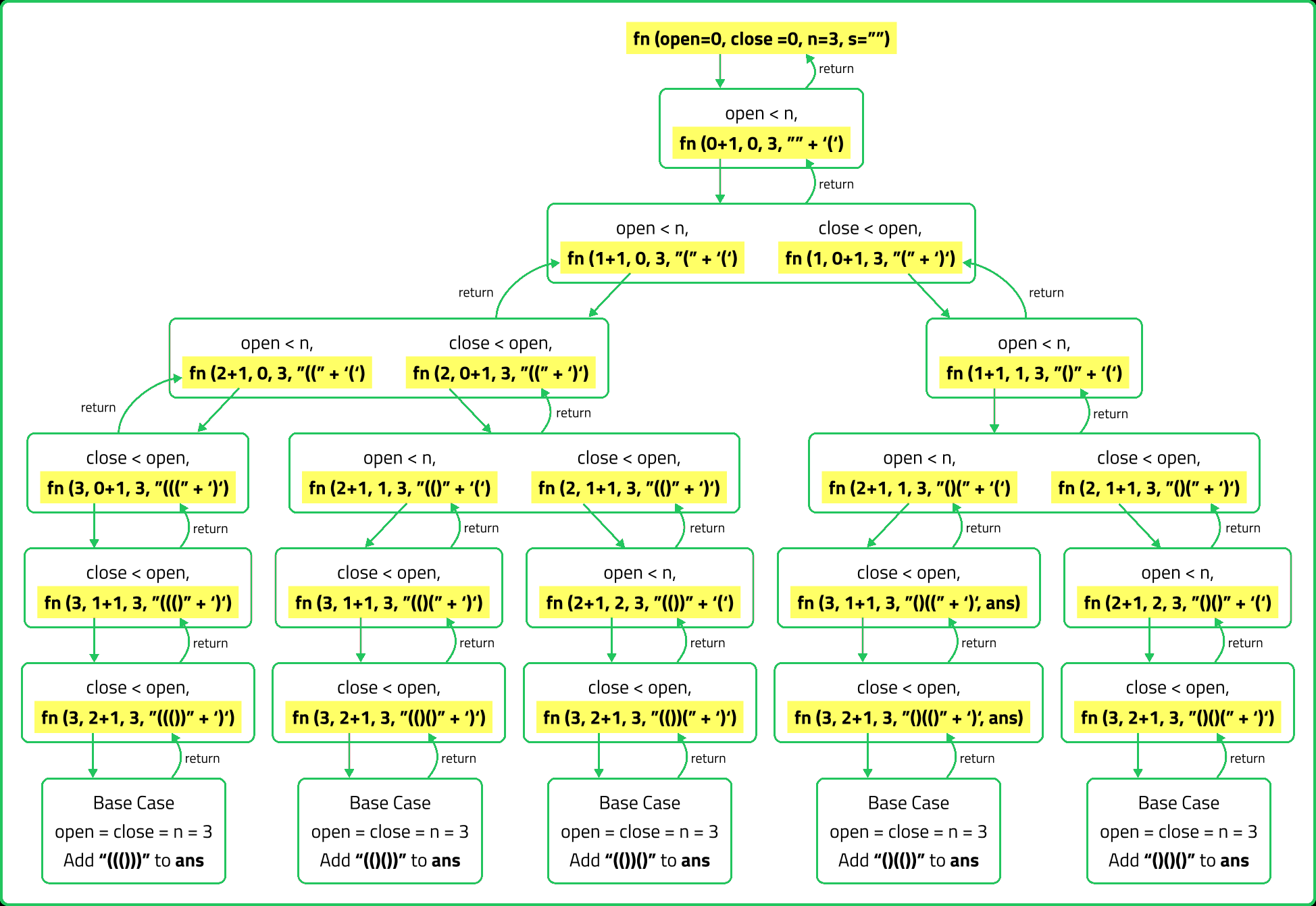
Generate Paranthesis

Recursion Implementation Problems Easy

Fun Fact: The concept behind well-formed parentheses is key in developing various software tools, especially in language parsing libraries and compilers
Programmers often deal with nested structures like functions, loops, and conditionals in coding, which are represented using parentheses, braces, etc
The formation or validation of these correctly structured parentheses and other symbols is of utmost importance for the correct interpretation of the code
Similarly, tools for checking the validity of XML or JSON also use this concept to ensure the correct pairing and nesting of tags and braces

Given an integer n.Generate all possible combinations of well-formed parentheses of length 2 x N.

Examples:

Input : n = 3

Output : [ "((()))" , "(()())" , "(())()" , "()(())" , "()()()" ]

Input : 2

Output : [ "(())" , "()()" ]

Input : 1

Constraints

1 <= n <= 8

Hints

Start with an empty string and keep adding ( or ) recursively. If the string has 2×n characters, add it to the result.
Use a backtracking approach where you explore all possibilities and backtrack when the current combination is invalid.

Company Tags

Reddit Texas Instruments DoorDash Lyft Philips Healthcare PayPal Splunk Rakuten Zomato Etsy Walmart American Express Flipkart Stripe KPMG Siemens Healthineers Zoho Intel Uber Epic Systems Unity Technologies Boston Consulting Group Bungie Cerner Freshworks TCS Cognizant Accenture Infosys Capgemini Wipro

Editorial

              document.body.innerHTML = '';
              const iframeHTML = `
                <div style="padding-top:56.25%;position:relative;">
                  <iframe 
                    src="https://app.tpstreams.com/embed/atsjxr/6ZEFCYAhAsh/?access_token=33e345b1-9f22-4382-8c5c-7e49a75d8027" 
                    style="border:0;max-width:100%;position:absolute;top:0;left:0;height:100%;width:100%;" 
                    allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" 
                    allowfullscreen="" 
                    frameborder="0">
                  </iframe>
                </div>
              `;
              document.body.innerHTML = iframeHTML;
              
              const script = document.createElement('script');
              script.src = 'https://static.testpress.in/static/js/player.js';
              document.head.appendChild(script);
              
              script.onload = () => {
                const iframe = document.querySelector('iframe');
                const player = new Testpress.Player(iframe);
              
                player.loaded().then(() => {
                  console.log('Player is ready now');
                });
              
                player.on('play', () => {
                  console.log('Played the video');
                });
              };

Real-Life Intuition

To understand the problem better visualize arranging a set of opening and closing brackets to form valid sequences. Think of it like scheduling tasks where each scheduled meeting needs a corresponding end time. To solve this, start with an empty schedule (or an opening bracket) and recursively decide whether to add a meeting (an opening bracket if more are allowed) or a not scheduled one (closing bracket if it pairs with an existing opening bracket). Each step ensures that the schedule remains balanced and all meetings are correctly paired. This approach systematically explores all possible valid sequences by following rules similar to ensuring that every start time has an end time, and no end time precedes a start time.

Approach

Begin with zero open and zero close parentheses. Initialize an empty string and a list to store the valid combinations.
At each step, decide to add an open parenthesis if there are more available. Add a close parenthesis if it is valid (i.e., if the number of close parentheses used is less than the number of open parentheses).
Base Case: When the number of open and close parentheses used equals the total number of pairs, the current string is a valid combination. Add this string to the list of results.
Recursive Calls: Use recursion to explore both adding an open parenthesis and adding a close parenthesis, if permissible, to build all possible valid combinations.

Dry Run

Solution

#include<bits/stdc++.h>
using namespace std;

class Solution {
private: 
    /**
     * A recursive helper function to generate all combinations
     * of balanced parentheses.
     *
     * @param open The number of open parentheses used so far.
     * @param close The number of close parentheses used so far.
     * @param n The total number of pairs of parentheses.
     * @param s The current string being built.
     * @param ans The vector storing all valid combinations.
     */
    void func(int open, int close, int n, string s, vector<string> &ans) {
        // Base case: if the number of open and close parentheses used
        // is equal to the total number of pairs, add the string to the result.
        if (open == close && (open + close) == 2 * n) {
            ans.push_back(s); 
            return; 
        }
        
        // If the number of open parentheses used is less than the total
        // number of pairs, add an open parenthesis and call the function recursively.
        if (open < n) {
            func(open + 1, close, n, s + '(', ans); 
        }
        
        // If the number of close parentheses used is less than the number
        // of open parentheses, add a close parenthesis and call the function recursively.
        if (close < open) {
            func(open, close + 1, n, s + ')', ans); 
        }
    }
public:
    /**
     * Generates all combinations of n pairs of balanced parentheses.
     *
     * @param n The number of pairs of parentheses.
     * @return A vector containing all valid combinations of parentheses.
     */
    vector<string> generateParenthesis(int n) {
        // Vector to store the result
        vector<string> ans; 
        // Start the recursive generation with initial values
        func(0, 0, n, "", ans); 
        return ans; 
    }
};

int main() {
    Solution sol;
    int n = 3; // Example input
    vector<string> result = sol.generateParenthesis(n);

    cout << "All combinations of balanced parentheses for n = " << n << " are:" << endl;
    for (const string &combination : result) {
        cout << combination << endl;
    }

    return 0;
}
import java.util.ArrayList;
import java.util.List;

class Solution {
    public List<String> generateParenthesis(int n) {
        /**
         * Generates all combinations of n pairs of balanced parentheses.
         *
         * @param n The number of pairs of parentheses.
         * @return A list containing all valid combinations of parentheses.
         */
        List<String> result = new ArrayList<>();
        // Start the recursive generation with initial values
        generate(0, 0, n, "", result);
        return result;
    }

    private void generate(int open, int close, int n, String current, List<String> result) {
        /**
         * A recursive helper function to generate all combinations
         * of balanced parentheses.
         *
         * @param open The number of open parentheses used so far.
         * @param close The number of close parentheses used so far.
         * @param n The total number of pairs of parentheses.
         * @param current The current string being built.
         * @param result The list storing all valid combinations.
         */
        // Base case: if the number of open and close parentheses used
        // is equal to the total number of pairs, add the string to the result.
        if (open == close && open + close == 2 * n) {
            result.add(current);
            return;
        }

        // If the number of open parentheses used is less than the total
        // number of pairs, add an open parenthesis and call the function recursively.
        if (open < n) {
            generate(open + 1, close, n, current + '(', result);
        }

        // If the number of close parentheses used is less than the number
        // of open parentheses, add a close parenthesis and call the function recursively.
        if (close < open) {
            generate(open, close + 1, n, current + ')', result);
        }
    }

    public static void main(String[] args) {
        Solution sol = new Solution();
        int n = 3; // Example input
        List<String> result = sol.generateParenthesis(n);

        System.out.println("All combinations of balanced parentheses for n = " + n + " are:");
        for (String combination : result) {
            System.out.println(combination);
        }
    }
}
class Solution:
    def generateParenthesis(self, n: int):
        """
        Generates all combinations of n pairs of balanced parentheses.
        
        :param n: The number of pairs of parentheses.
        :return: A list containing all valid combinations of parentheses.
        """
        # List to store the result
        ans = []
        # Start the recursive generation with initial values
        self._generate(0, 0, n, "", ans)
        return ans

    def _generate(self, open_count: int, close_count: int, n: int, current: str, ans: list):
        """
        A recursive helper function to generate all combinations
        of balanced parentheses.

        :param open_count: The number of open parentheses used so far.
        :param close_count: The number of close parentheses used so far.
        :param n: The total number of pairs of parentheses.
        :param current: The current string being built.
        :param ans: The list storing all valid combinations.
        """
        # Base case: if the number of open and close parentheses used
        # is equal to the total number of pairs, add the string to the result.
        if open_count == close_count == n:
            ans.append(current)
            return

        # If the number of open parentheses used is less than the total
        # number of pairs, add an open parenthesis and call the function recursively.
        if open_count < n:
            self._generate(open_count + 1, close_count, n, current + '(', ans)

        # If the number of close parentheses used is less than the number
        # of open parentheses, add a close parenthesis and call the function recursively.
        if close_count < open_count:
            self._generate(open_count, close_count + 1, n, current + ')', ans)


# Example usage
if __name__ == "__main__":
    sol = Solution()
    n = 3  # Example input
    result = sol.generateParenthesis(n)

    print(f"All combinations of balanced parentheses for n = {n} are:")
    for combination in result:
        print(combination)
class Solution {
    /**
     * Generates all combinations of n pairs of balanced parentheses.
     *
     * @param {number} n The number of pairs of parentheses.
     * @returns {string[]} An array containing all valid combinations of parentheses.
     */
    generateParenthesis(n) {
        // Array to store the result
        const results = [];
        // Start the recursive generation with initial values
        this.generate('', n, n, results);
        // Sorting the results to maintain a consistent order
        return results.sort();
    }

    /**
     * A recursive helper function to generate all combinations
     * of balanced parentheses.
     *
     * @param {string} current The current string being built.
     * @param {number} open The number of open parentheses left to add.
     * @param {number} close The number of close parentheses left to add.
     * @param {string[]} results The array storing all valid combinations.
     */
    generate(current, open, close, results) {
        // Base case: if no open or close parentheses are left,
        // add the current string to the results array.
        if (open === 0 && close === 0) {
            results.push(current);
            return;
        }

        // If there are open parentheses left to add,
        // add an open parenthesis and call the function recursively.
        if (open > 0) {
            this.generate(current + '(', open - 1, close, results);
        }

        // If the number of close parentheses left is greater than
        // the number of open parentheses left, add a close parenthesis
        // and call the function recursively.
        if (close > open) {
            this.generate(current + ')', open, close - 1, results);
        }
    }
}

// Example usage:
const sol = new Solution();
const n = 3; // Example input
const result = sol.generateParenthesis(n);

console.log("All combinations of balanced parentheses for n =", n, "are:");
console.log(result.join('\n'));

Complexity Analysis

Time Complexity: O(4^n / sqrt(n)), where n is the number of pairs of parentheses. This complexity arises because each step involves branching into two possibilities, resulting in an exponential number of possibilities, reduced by the Catalan number formula for valid combinations.

Space Complexity: O(4^n / sqrt(n)), primarily due to the recursion stack and the storage required for the result list of valid combinations. The space is proportional to the number of valid combinations generated.

Code

Problem List