12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394
#include<bits/stdc++.h>
using namespace std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
vector<vector<int>> verticalTraversal(TreeNode* root) {
// List to store the final result
vector<vector<int>> result;
if (root == nullptr) {
return result;
}
// Map to store the nodes at each vertical distance and level
map<int, map<int, priority_queue<int, vector<int>, greater<int>>>> nodesMap;
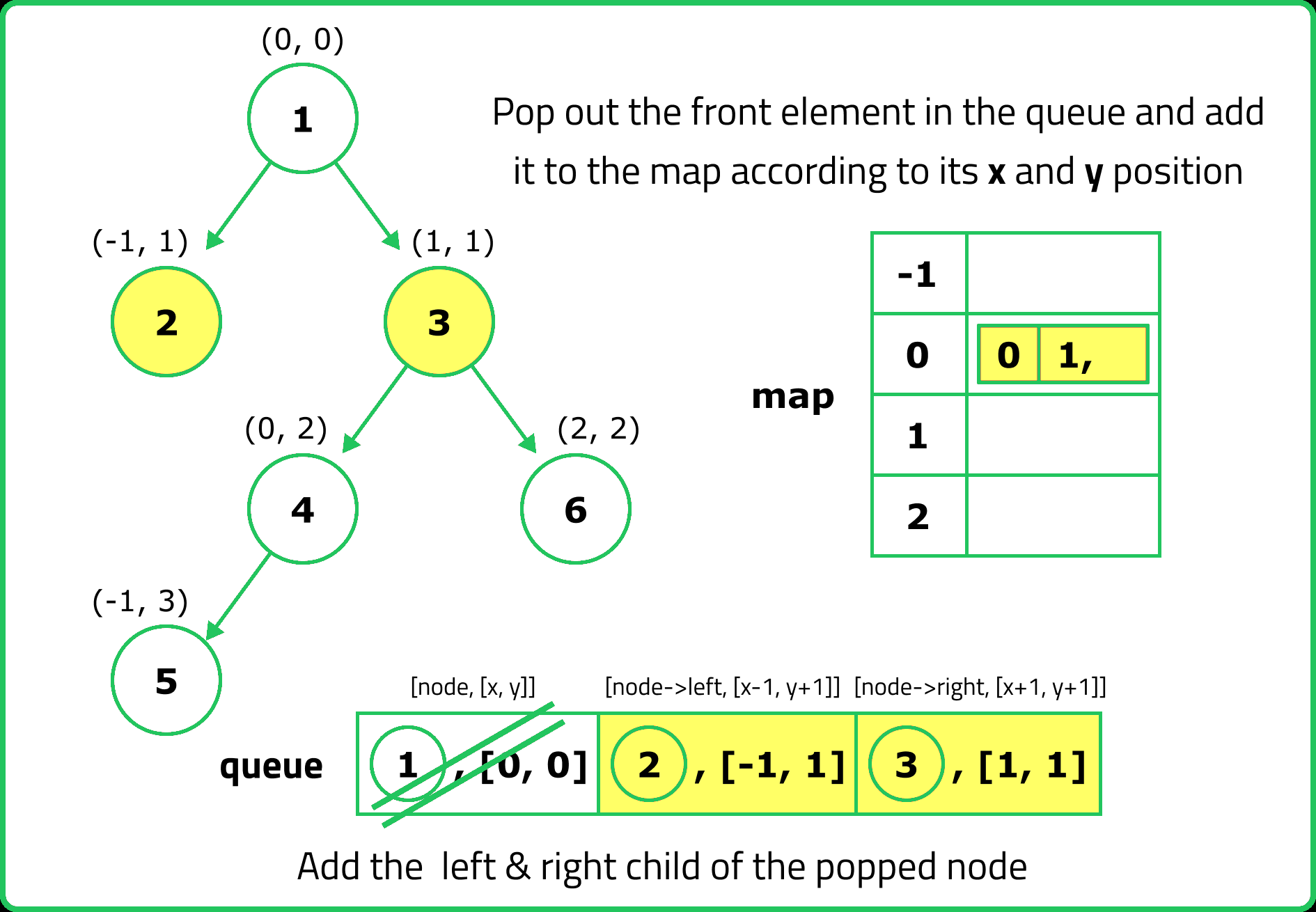
// Queue for BFS traversal (stores node along with its x and y coordinates)
queue<pair<TreeNode*, pair<int, int>>> q;
q.push({root, {0, 0}}); // (node, {x, y})
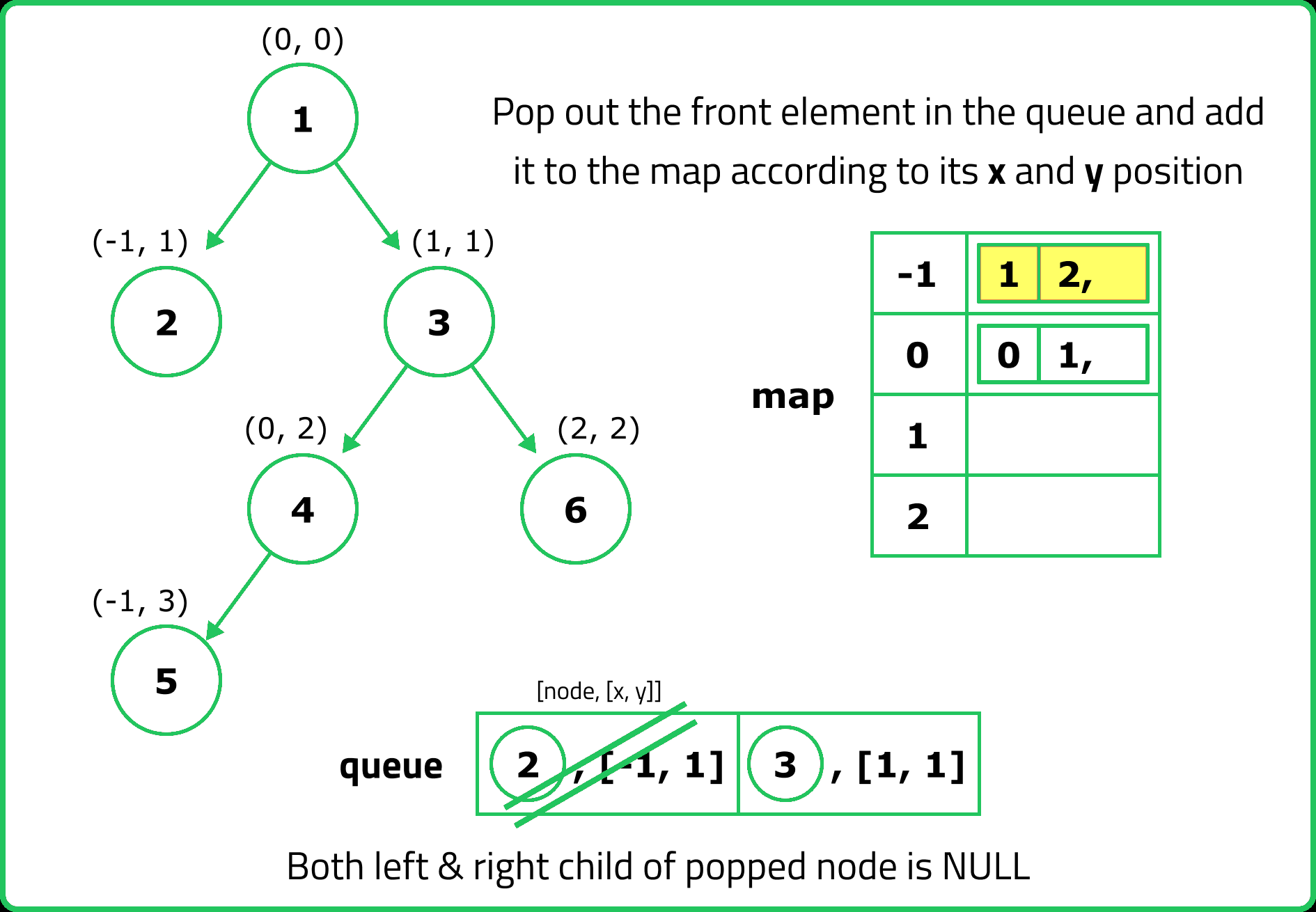
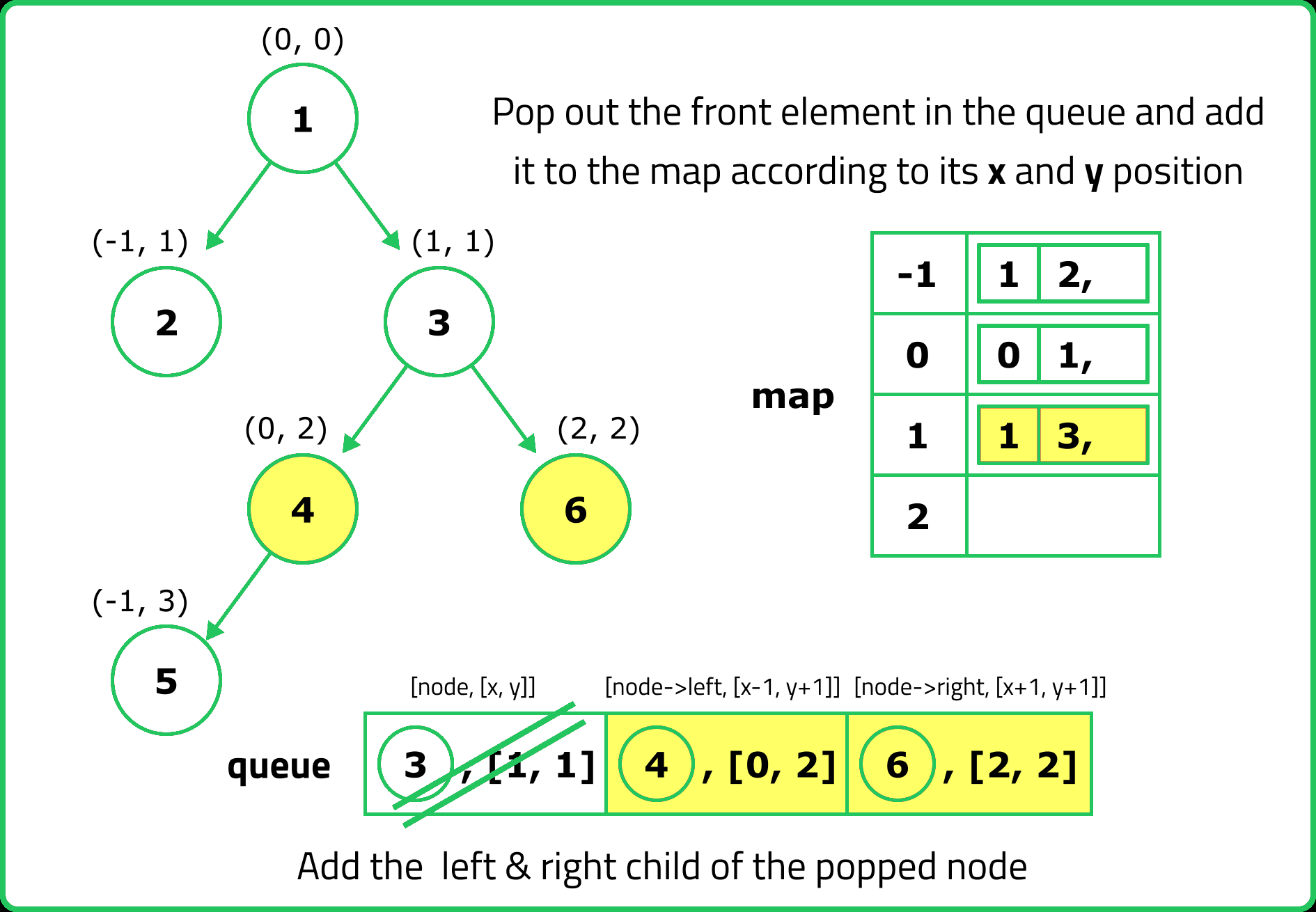
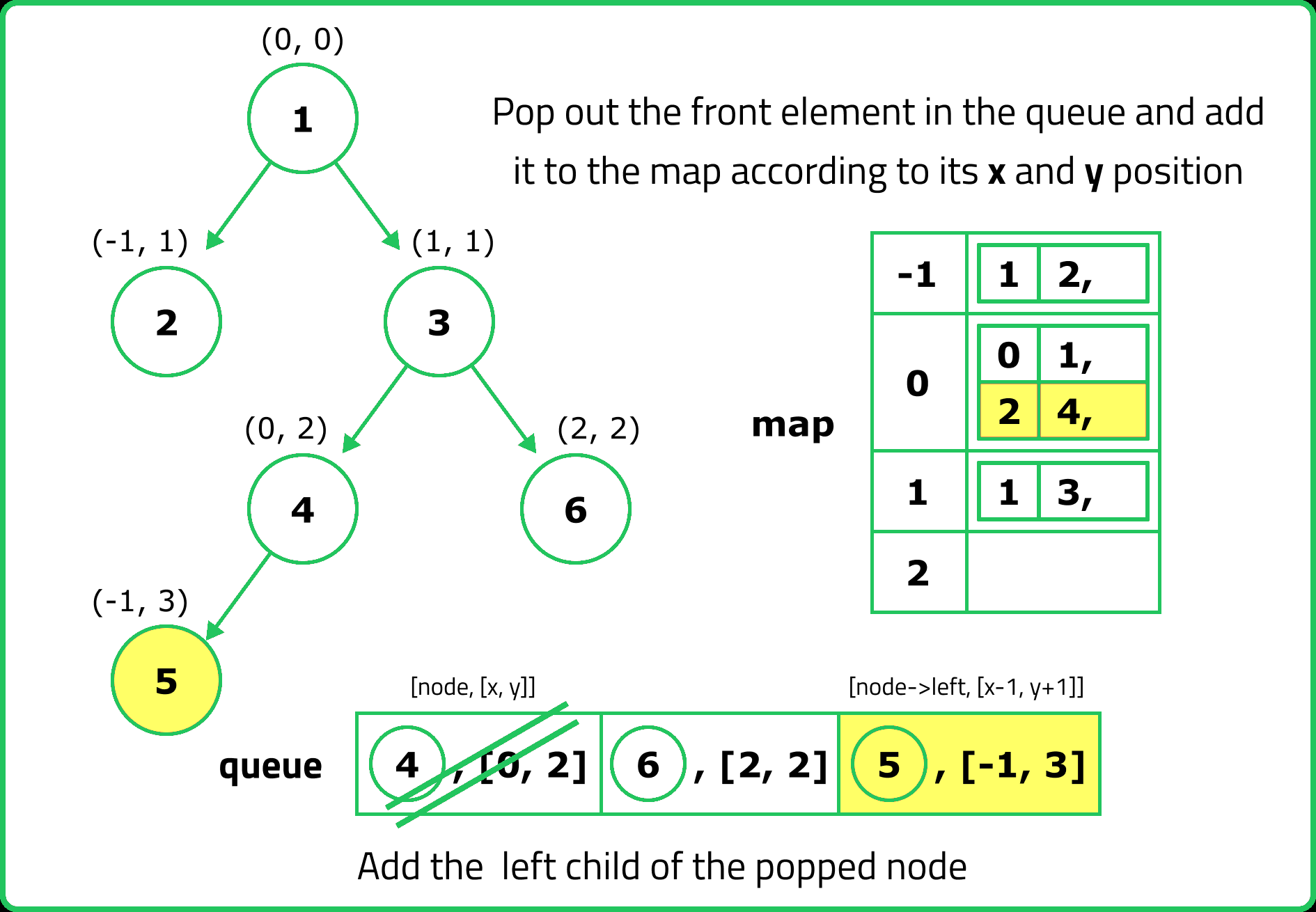
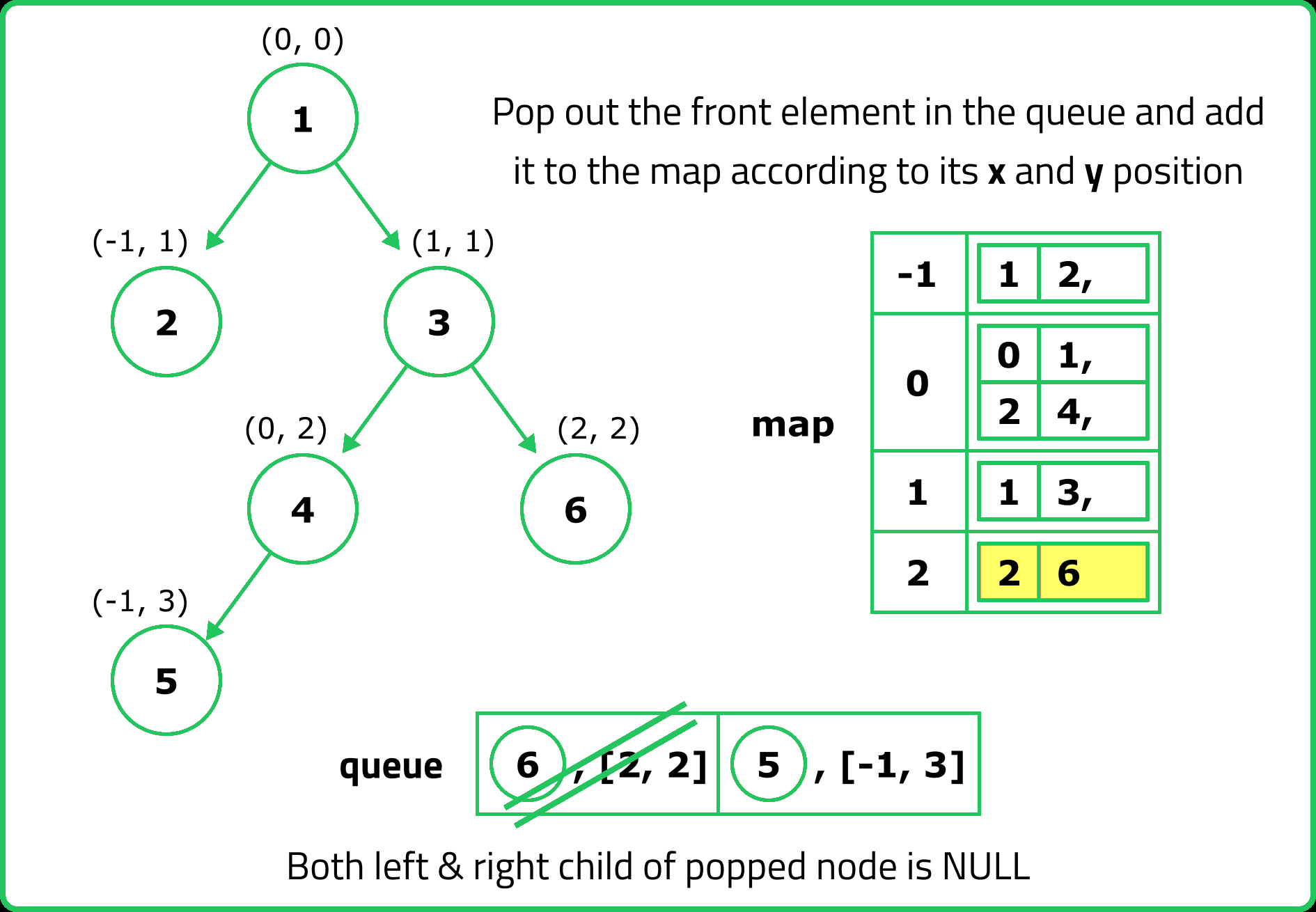
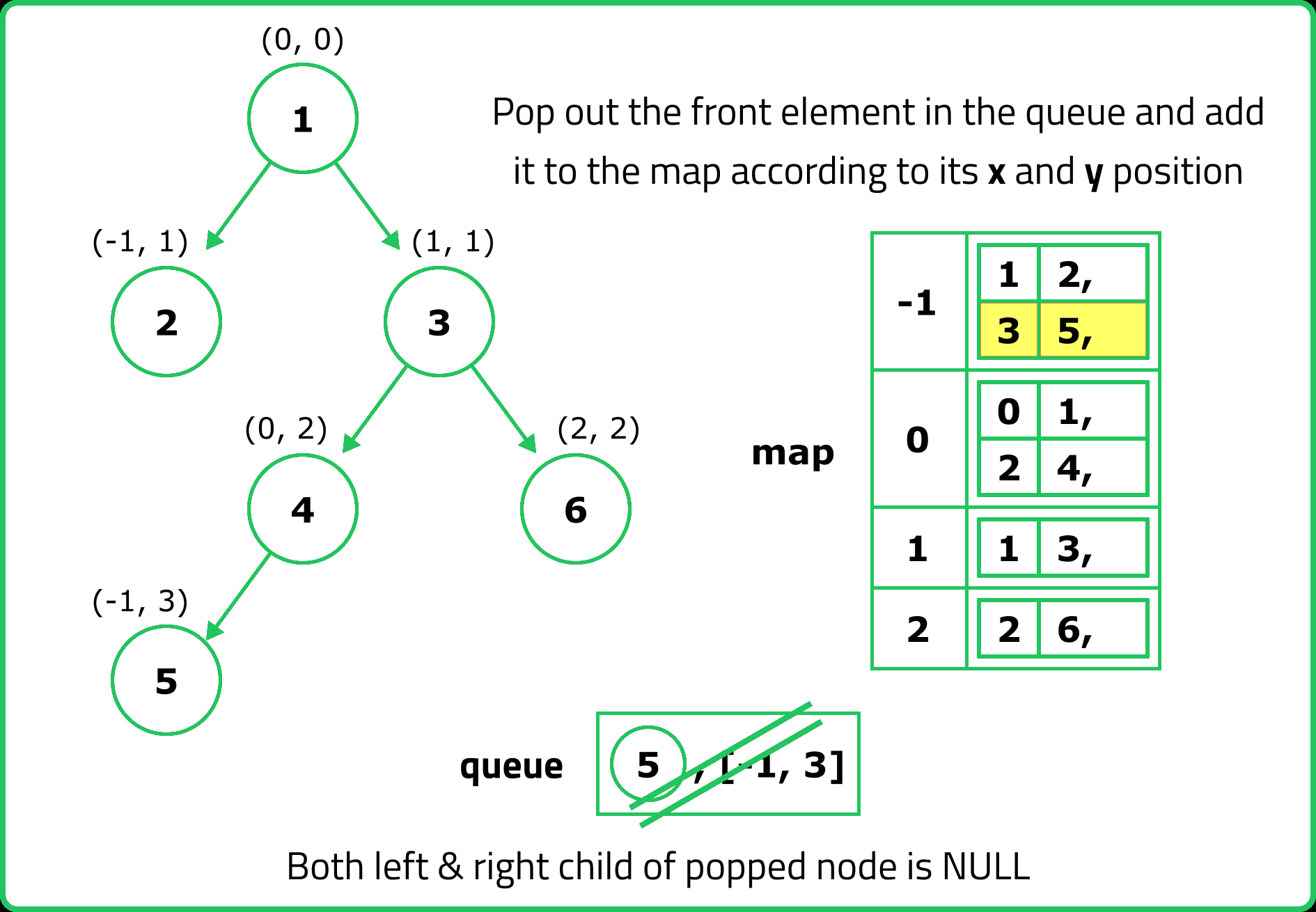
// Perform BFS
while (!q.empty()) {
auto p = q.front();
q.pop();
TreeNode* node = p.first;
int x = p.second.first;
int y = p.second.second;
// Add the node's value to the map at the correct x and y
nodesMap[x][y].push(node->data);
// Add the left child with updated coordinates to the queue
if (node->left != nullptr) {
q.push({node->left, {x - 1, y + 1}});
}
// Add the right child with updated coordinates to the queue
if (node->right != nullptr) {
q.push({node->right, {x + 1, y + 1}});
}
}
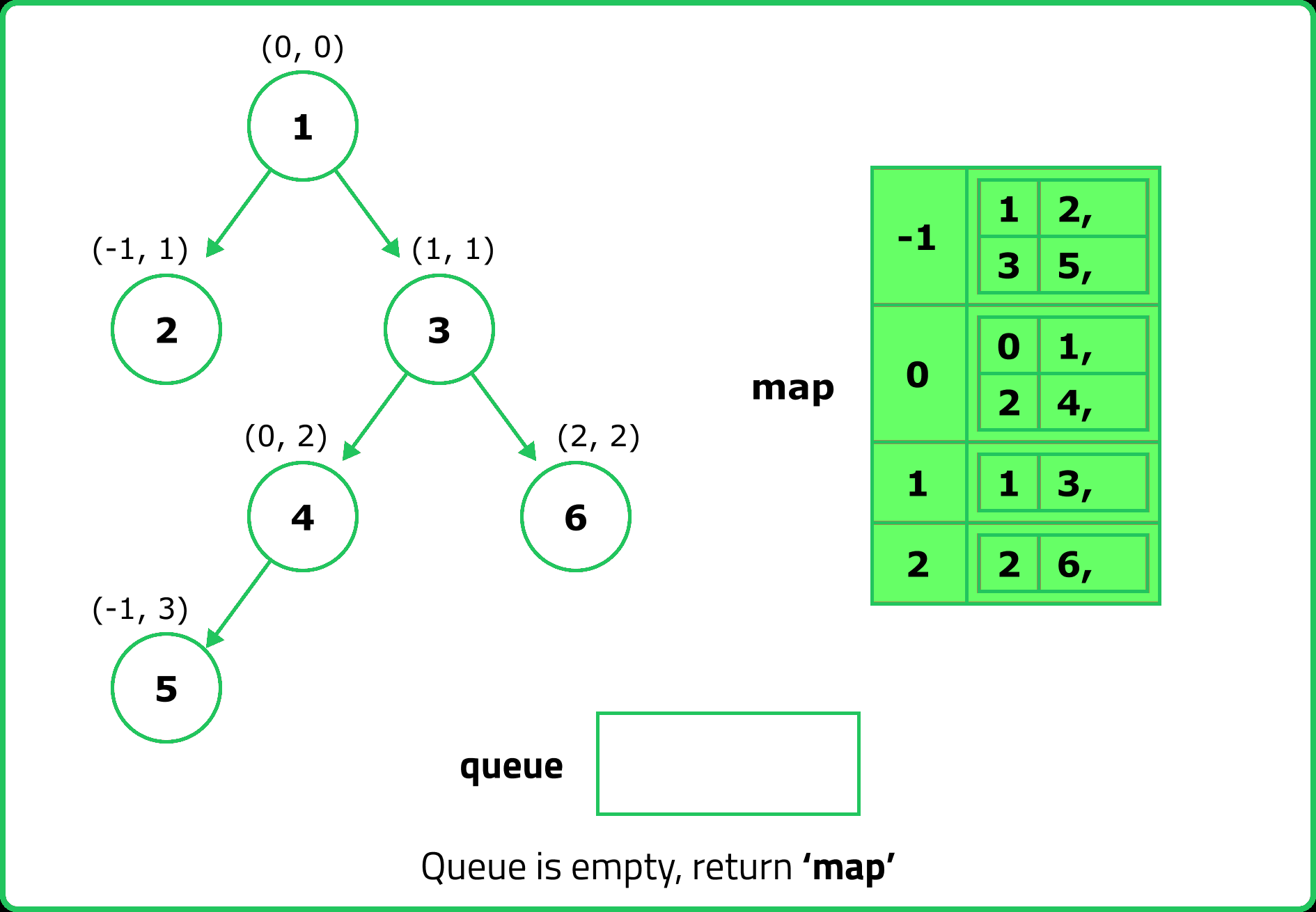
// Prepare the result by sorting keys and compiling nodes
for (auto& p : nodesMap) {
vector<int> column;
for (auto& q : p.second) {
while (!q.second.empty()) {
column.push_back(q.second.top());
q.second.pop();
}
}
result.push_back(column);
}
return result;
}
};
// Main method to test the verticalTraversal function
int main() {
// Creating a binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
root->right->right = new TreeNode(7);
// Creating an instance of Solution
Solution sol;
// Getting the vertical order traversal
vector<vector<int>> result = sol.verticalTraversal(root);
// Printing the result
cout << "Vertical Order Traversal: " << endl;
for (const auto& col : result) {
for (int num : col) {
cout << num << " ";
}
cout << endl;
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100
import java.util.*;
class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
// Nested static class Tuple
static class Tuple {
TreeNode node;
int x; // Vertical distance
int y; // Level
Tuple(TreeNode node, int x, int y) {
this.node = node;
this.x = x;
this.y = y;
}
}
public List<List<Integer>> verticalTraversal(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
// TreeMap to store the nodes at each vertical distance
TreeMap<Integer, TreeMap<Integer, PriorityQueue<Integer>>> nodesMap = new TreeMap<>();
// Queue for BFS traversal (stores node along with its x and y coordinates)
Queue<Tuple> queue = new LinkedList<>();
queue.offer(new Tuple(root, 0, 0)); // (node, x, y)
// Perform BFS
while (!queue.isEmpty()) {
Tuple tuple = queue.poll();
TreeNode node = tuple.node;
int x = tuple.x;
int y = tuple.y;
// Add the node's value to the map at the correct x and y
nodesMap.putIfAbsent(x, new TreeMap<>());
nodesMap.get(x).putIfAbsent(y, new PriorityQueue<>());
nodesMap.get(x).get(y).offer(node.data);
// Add the left child with updated coordinates to the queue
if (node.left != null) {
queue.offer(new Tuple(node.left, x - 1, y + 1));
}
// Add the right child with updated coordinates to the queue
if (node.right != null) {
queue.offer(new Tuple(node.right, x + 1, y + 1));
}
}
// Prepare the result by sorting keys and compiling nodes
for (TreeMap<Integer, PriorityQueue<Integer>> yMap : nodesMap.values()) {
List<Integer> column = new ArrayList<>();
for (PriorityQueue<Integer> nodes : yMap.values()) {
while (!nodes.isEmpty()) {
column.add(nodes.poll());
}
}
result.add(column);
}
return result;
}
}
class Main {
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);
Solution solution = new Solution();
List<List<Integer>> result = solution.verticalTraversal(root);
System.out.println("Vertical Traversal:");
for (List column : result) {
System.out.println(column);
}
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
from collections import defaultdict, deque
# Definition for a binary tree node.
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
def verticalTraversal(self, root):
"""
Perform vertical order traversal of a binary tree.
:param root: TreeNode - The root of the binary tree.
:return: List[List[int]] - A list of lists containing the vertical order traversal.
"""
if not root:
return []
# Dictionary to store the nodes at each vertical distance and level.
# nodes_map[x][y] will hold a list of nodes at vertical distance x and level y.
nodes_map = defaultdict(lambda: defaultdict(list))
# Queue for BFS traversal (stores node along with its x and y coordinates)
queue = deque([(root, 0, 0)]) # (node, x, y)
# Perform BFS to populate nodes_map with nodes at each (x, y) coordinate.
while queue:
node, x, y = queue.popleft()
# Add the node's value to the map at the correct x and y
nodes_map[x][y].append(node.data)
# Add the left child with updated coordinates to the queue
if node.left:
queue.append((node.left, x - 1, y + 1))
# Add the right child with updated coordinates to the queue
if node.right:
queue.append((node.right, x + 1, y + 1))
# Prepare the result by sorting keys and compiling nodes
result = []
for x in sorted(nodes_map):
column = []
for y in sorted(nodes_map[x]):
# Sort the nodes at the same position to maintain the order
column.extend(sorted(nodes_map[x][y]))
result.append(column)
return result
# Main method to test the verticalTraversal function
if __name__ == "__main__":
# Creating a binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
root.right.right = TreeNode(7)
# Creating an instance of Solution
sol = Solution()
# Getting the vertical order traversal
result = sol.verticalTraversal(root)
# Printing the result
print("Vertical Order Traversal:", result)
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null){
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
verticalTraversal(root) {
// If the root is null, return an empty array
if (!root) {
return [];
}
// Map to store the nodes at each vertical distance and level
const nodesMap = new Map();
// Queue for BFS traversal (stores node along with its x and y coordinates)
const queue = [{ node: root, x: 0, y: 0 }];
// Perform BFS
while (queue.length > 0) {
const { node, x, y } = queue.shift();
// Add the node's value to the map at the correct x and y
if (!nodesMap.has(x)) {
nodesMap.set(x, new Map());
}
if (!nodesMap.get(x).has(y)) {
nodesMap.get(x).set(y, []);
}
nodesMap.get(x).get(y).push(node.data);
// Add the left child with updated coordinates to the queue
if (node.left) {
queue.push({ node: node.left, x: x - 1, y: y + 1 });
}
// Add the right child with updated coordinates to the queue
if (node.right) {
queue.push({ node: node.right, x: x + 1, y: y + 1 });
}
}
// Prepare the result by sorting keys and compiling nodes
const result = [];
const sortedXKeys = Array.from(nodesMap.keys()).sort((a, b) => a - b);
for (const x of sortedXKeys) {
const yMap = nodesMap.get(x);
const sortedYKeys = Array.from(yMap.keys()).sort((a, b) => a - b);
const column = [];
for (const y of sortedYKeys) {
const nodes = yMap.get(y);
nodes.sort((a, b) => a - b);
column.push(...nodes);
}
result.push(column);
}
return result;
}
}
// Main method to test the verticalTraversal function
// Creating a binary tree
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);
// Creating an instance of Solution
const sol = new Solution();
// Getting the vertical order traversal
const result = sol.verticalTraversal(root);
// Printing the result
console.log("Vertical Order Traversal:", result);