3 Sum

Intuition

The most naive idea is to check all possible triplets using 3 loops and among them, consider the ones whose sum is equal to the given target 0.

Before taking them as the answer, sort the triplets in ascending order so as to consider only the unique triplets.

Approach

Declare a set data structure for storing the unique triplets.

Used nested loopinf structure to traverse the array, and take triplets into account.

First loop will run from 0th index till the length of array, lets call it i. Inside it, there will be the another loop(say j) that will run from i+1 to n-1. Then a third loop(say k) that runs from j+1 to n-1.

Now, inside these 3 nested loops, check the sum of arr[i] and arr[j] and arr[k], and if it is equal to the target i.e. 0 sort this triplet and insert it in the set data structure. Finally, return the list of triplets stored in the set data structure.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find triplets having sum equals to target
    vector<vector<int>> threeSum(vector<int>& nums) {
        // Set to store unique triplets
        set<vector<int>> tripletSet;

        int n = nums.size();

        // Check all possible triplets
        for (int i = 0; i < n - 2; i++) {
            for (int j = i + 1; j < n - 1; j++) {
                for (int k = j + 1; k < n; k++) {
                    if (nums[i] + nums[j] + nums[k] == 0) {
                        // Found a triplet that sums up to target
                        vector<int> temp = {nums[i], nums[j], nums[k]};
                        
                        /* Sort the triplet to ensure
                         uniqueness when storing in set*/
                        sort(temp.begin(), temp.end());
                        tripletSet.insert(temp);
                        
                    }
                }
            }
        }

        // Convert set to vector (unique triplets)
        vector<vector<int>> ans(tripletSet.begin(), tripletSet.end());

       //Return the ans
        return ans;
    }
};

int main() {
    vector<int> nums = {-1, 0, 1, 2, -1, -4};

    // Create an instance of Solution class
    Solution sol;

    vector<vector<int>> ans = sol.threeSum(nums);

    // Print the result
    for (auto& triplet : ans) {
        cout << "[";
        for (auto& num : triplet) {
            cout << num << " ";
        }
        cout << "] ";
    }
    cout << "\n";

    return 0;
}
import java.util.*;

class Solution {
    //Function to find triplets having sum equals to target
    public List<List<Integer>> threeSum(int[] nums) {
        // Set to store unique triplets
        Set<List<Integer>> tripletSet = new HashSet<>();

        int n = nums.length;

        // Check all possible triplets
        for (int i = 0; i < n - 2; i++) {
            for (int j = i + 1; j < n - 1; j++) {
                for (int k = j + 1; k < n; k++) {
                    if (nums[i] + nums[j] + nums[k] == 0) {
                        // Found a triplet that sums up to target
                        List<Integer> temp = new ArrayList<>();
                        temp.add(nums[i]);
                        temp.add(nums[j]);
                        temp.add(nums[k]);
                        
                        /* Sort the triplet to ensure 
                        uniqueness when storing in set*/
                        Collections.sort(temp);
                        tripletSet.add(temp);
                    }
                }
            }
        }

        // Convert set to list of lists (unique triplets)
        List<List<Integer>> ans = new ArrayList<>(tripletSet);

        //Return the ans
        return ans;
    }
}

public class Main {
    public static void main(String[] args) {
        int[] nums = {-1, 0, 1, 2, -1, -4};

        // Create an instance of Solution class
        Solution sol = new Solution();

        List<List<Integer>> ans = sol.threeSum(nums);

        // Print the result
        for (List<Integer> triplet : ans) {
            System.out.print("[");
            for (int num : triplet) {
                System.out.print(num + " ");
            }
            System.out.print("] ");
        }
        System.out.println();
    }
}
from typing import List

class Solution:
    #Function to find triplets having sum equals to target
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        # Set to store unique triplets
        triplet_set = set()

        n = len(nums)

        # Check all possible triplets
        for i in range(n - 2):
            for j in range(i + 1, n - 1):
                for k in range(j + 1, n):
                    if nums[i] + nums[j] + nums[k] == 0:
                        # Found a triplet that sums up to target
                        temp = [nums[i], nums[j], nums[k]]
                        
                        """ Sort the triplet to ensure 
                        uniqueness when storing in set"""
                        temp.sort()
                        triplet_set.add(tuple(temp))
        
        # Convert set to list of lists (unique triplets)
        ans = [list(triplet) for triplet in triplet_set]

        #Return the ans
        return ans

if __name__ == "__main__":
    nums = [-1, 0, 1, 2, -1, -4]

    # Create an instance of Solution class
    sol = Solution()


    ans = sol.threeSum(nums)

    # Print the result
    for triplet in ans:
        print(f"[{', '.join(map(str, triplet))}]")
class Solution {
    // Function to find triplets having sum equals to target
    threeSum(nums) {
        // Set to store unique triplets
        let tripletSet = new Set();

        let n = nums.length;

        // Check all possible triplets
        for (let i = 0; i < n - 2; i++) {
            for (let j = i + 1; j < n - 1; j++) {
                for (let k = j + 1; k < n; k++) {
                    if (nums[i] + nums[j] + nums[k] === 0) {
                        // Found a triplet that sums up to target
                        let temp = [nums[i], nums[j], nums[k]];
                        
                        /* Sort the triplet to ensure
                        uniqueness when storing in set*/
                        temp.sort((a, b) => a - b);
                        tripletSet.add(temp.join(','));
                    }
                }
            }
        }

        // Convert set to array of arrays (unique triplets)
        let ans = Array.from(tripletSet).map(triplet => triplet.split(',').map(num => parseInt(num)));

        // Return the ans
        return ans;
    }
}

// Main function to test the solution
let nums = [-1, 0, 1, 2, -1, -4];

// Create an instance of Solution class
let sol = new Solution();

let ans = sol.threeSum(nums);

// Print the result
ans.forEach(triplet => {
    console.log(`[${triplet.join(', ')}]`);
});

Complexity Analyis

Time Complexity: O(N³ x log(no. of unique triplets)), where N is size of the array. Using 3 nested loops & inserting triplets into the set takes O(log(no. of unique triplets)) time complexity. But we are not considering the time complexity of sorting as we are just sorting 3 elements every time. Space Complexity: O(2 x no. of the unique triplets) for using a set data structure and a list to store the triplets.

Intuition

The better approach uses simple mathematics where some calculative parameter is taken in RHS(right hand side) to compute the result.

For example if a + b + c = 0, then a + b = -c. Similar idea is used here.

Approach

Declare a set data structure to store unique triplets. Then iterate in the array lets call the variable i from index 0 to n -1. Inside it, there will be the second loop(say j) that will run from i+1 to n-1.

Declare another HashSet to store the array elements as we intend to search for the third element using this HashSet.

Inside the nested loop, calculate the value of the third element i.e. -(arr[i]+arr[j]).

If the third element exists in the HashSet, sort these 3 values i.e. arr[i], arr[j], and the third element, and insert it in the set data structure declared in step 1.

After that, insert the j-th element i.e. arr[j] in the HashSet as we only want to insert those array elements that are in between indices i and j. Finally, return a list of triplets stored in the set data structure.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to find triplets having sum equals to target
    vector<vector<int>> threeSum(vector<int>& nums) {
        // Set to store unique triplets
        set<vector<int>> tripletSet;

        int n = nums.size();

        // Check all possible triplets
        for (int i = 0; i < n; i++) {
            // Set to store elements seen so far in the loop
            set<int> hashset;

            for (int j = i + 1; j < n; j++) {
                // Calculate the 3rd element needed to reach target
                int third = - (nums[i] + nums[j]);

                /* Find if third element exists in
                hashset (complements seen so far)*/
                if (hashset.find(third) != hashset.end()) {
                    // Found a triplet that sums up to target
                    vector<int> temp = {nums[i], nums[j], third};
                    
                    /* Sort the triplet to ensure 
                    uniqueness when storing in set*/
                    sort(temp.begin(), temp.end());
                    tripletSet.insert(temp);
                }
                
                /* Insert the current element
                into hashset for future checks*/
                hashset.insert(nums[j]);
            }
        }

        // Convert set to vector (unique triplets)
        vector<vector<int>> ans(tripletSet.begin(), tripletSet.end());

        //Return the ans
        return ans;
    }
};

int main() {
    vector<int> nums = {-1, 0, 1, 2, -1, -4};

    // Create an instance of Solution class
    Solution sol;

    vector<vector<int>> ans = sol.threeSum(nums);

    // Print the result
    for (auto& triplet : ans) {
        cout << "[";
        for (auto& num : triplet) {
            cout << num << " ";
        }
        cout << "] ";
    }
    cout << "\n";

    return 0;
}
import java.util.*;

class Solution {
    // Function to find triplets having sum equals to 0
    public List<List<Integer>> threeSum(int[] nums) {
        // Set to store unique triplets
        Set<List<Integer>> tripletSet = new HashSet<>();

        int n = nums.length;

        // Check all possible triplets
        for (int i = 0; i < n; i++) {
            // Set to store elements seen so far in the loop
            Set<Integer> hashset = new HashSet<>();

            for (int j = i + 1; j < n; j++) {
                // Calculate the 3rd element needed to reach 0
                int third =  - (nums[i] + nums[j]);

                /* Find if third element exists in
                hashset (complements seen so far)*/
                if (hashset.contains(third)) {
                    // Found a triplet that sums up to target
                    List<Integer> temp = new ArrayList<>();
                    temp.add(nums[i]);
                    temp.add(nums[j]);
                    temp.add(third);

                    /* Sort the triplet to ensure
                    uniqueness when storing in set*/
                    Collections.sort(temp);
                    tripletSet.add(temp);
                }

                /* Insert the current element 
                 into hashset for future checks*/
                hashset.add(nums[j]);
            }
        }

        // Convert set to list of lists (unique triplets)
        List<List<Integer>> ans = new ArrayList<>(tripletSet);

        //Return the ans
        return ans;
    }

    public static void main(String[] args) {
        int[] nums = {-1, 0, 1, 2, -1, -4};

        // Create an instance of Solution class
        Solution sol = new Solution();

        List<List<Integer>> ans = sol.threeSum(nums);

        // Print the result
        for (List<Integer> triplet : ans) {
            System.out.print("[");
            for (int num : triplet) {
                System.out.print(num + " ");
            }
            System.out.print("] ");
        }
        System.out.println();
    }
}
from typing import List

class Solution:
    # Function to find triplets having sum equals to 0
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        # Set to store unique triplets
        triplet_set = set()

        n = len(nums)

        # Check all possible triplets
        for i in range(n):
            # Set to store elements seen so far in the loop
            hashset = set()

            for j in range(i + 1, n):
                # Calculate the 3rd element needed to reach target
                third =  - (nums[i] + nums[j])

                """ Find if third element exists in
                 hashset (complements seen so far)"""
                if third in hashset:
                    # Found a triplet that sums up to target
                    temp = [nums[i], nums[j], third]

                    """ Sort the triplet to ensure
                    uniqueness when storing in set"""
                    temp.sort()
                    triplet_set.add(tuple(temp))

                """ Insert the current element 
                into hashset for future checks"""
                hashset.add(nums[j])

        # Convert set to list of lists (unique triplets)
        ans = [list(triplet) for triplet in triplet_set]

        #Return the ans
        return ans

if __name__ == "__main__":
    nums = [-1, 0, 1, 2, -1, -4]

    # Create an instance of Solution class
    sol = Solution()

    ans = sol.threeSum(nums)

    # Print the result
    for triplet in ans:
        print(f"[{', '.join(map(str, triplet))}]")
class Solution {
    // Function to find triplets having sum equals to 0
    threeSum(nums) {
        // Set to store unique triplets
        let tripletSet = new Set();

        let n = nums.length;

        // Check all possible triplets
        for (let i = 0; i < n; i++) {
            // Set to store elements seen so far in the loop
            let hashset = new Set();

            for (let j = i + 1; j < n; j++) {
                // Calculate the 3rd element needed to reach target
                let third =  - (nums[i] + nums[j]);

                /* Find if third element exists in 
                hashset (complements seen so far)*/
                if (hashset.has(third)) {
                    // Found a triplet that sums up to target
                    let temp = [nums[i], nums[j], third];

                    /* Sort the triplet to ensure 
                    uniqueness when storing in set*/
                    temp.sort((a, b) => a - b);
                    tripletSet.add(JSON.stringify(temp));
                }

                /* Insert the current element
                into hashset for future checks*/
                hashset.add(nums[j]);
            }
        }

        // Convert set to list of lists (unique triplets)
        let ans = Array.from(tripletSet).map(triplet => JSON.parse(triplet));

        //Return the ans
        return ans;
    }
}

// Main function to test the solution
let nums = [-1, 0, 1, 2, -1, -4];

// Create an instance of Solution class
let sol = new Solution();

let ans = sol.threeSum(nums);

// Print the result
ans.forEach(triplet => {
    console.log(`[${triplet.join(', ')}]`);
});

Complexity Analyis

Time Complexity: O(N^2 x log(no. of unique triplets)), where N is size of the array. Inserting triplets into the set takes O(log(no. of unique triplets)) time complexity. But we are not considering the time complexity of sorting as we are just sorting 3 elements every time. Space Complexity: O(2 x no. of the unique triplets) + O(N) for using a set data structure and a list to store the triplets and extra O(N) for storing the array elements in another set.

Intuition

Imagine you're organizing a dinner party and you want to create a balanced meal with three different ingredients that together have zero net calories.

First task would be to list all your ingredients by their calorie values and sort them. Then, for each ingredient, try to find two other ingredients from the remaining list that, when combined, balance the calories back to zero.

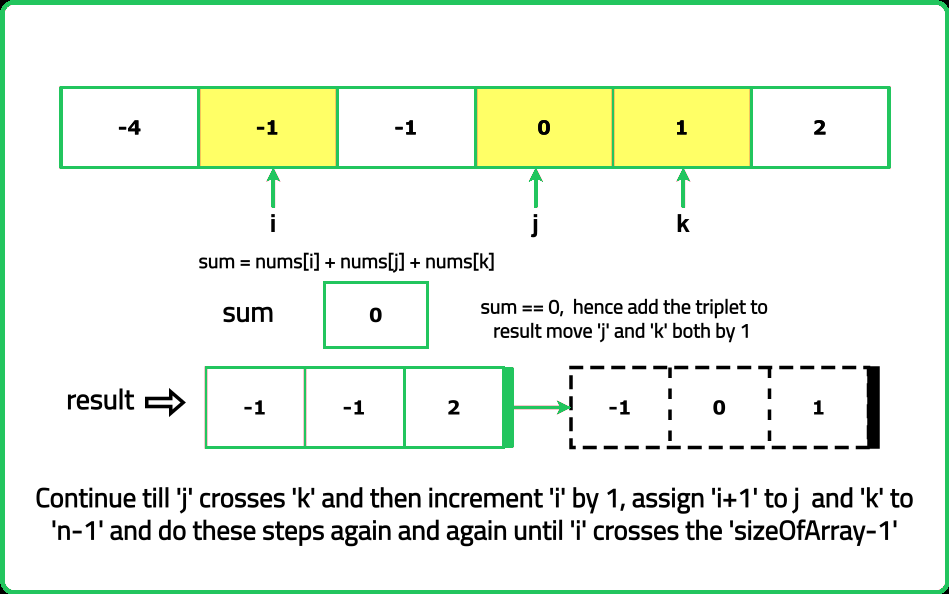
Start with one ingredient and use two pointers, one starting from the left (beginning of the list) and the other from the right (end of the list). By adjusting these pointers, check if the three chosen ingredients balance to zero calories. If they do, you have a balanced meal! Continue this process, ensuring that the same combination of ingredients more than once is not picked.

Approach

Sort the entire array & iterate from 0 to n-1 in the array, lets call the loop variable i. In each iteration, this value will be fixed for all different values of the rest of the 2 pointers.

Inside the loop, first check if the current and the previous element is the same and if it is, do nothing and continue to the next value of i.

After that, there will be 2 moving pointers i.e. j(starts from i+1) and k(starts from the last index). The pointer j will move forward and the pointer k will move backward until they cross each other while the value of i will be fixed.

Now check the sum of arr[i] and arr[j] and arr[k]. If the sum is exceeding target, then the ask is to use lesser valued elements and so decrease the value of k(i.e. k--). If the sum is lesser than the target, we need a bigger value and so increase the value of j (i.e. j++).

If the sum is equal to the target, simply insert the triplet i.e. arr[i], arr[j], arr[k] into answer data structure and move the pointers j and k skipping the duplicate elements(i.e. by checking the adjacent elements while moving the pointers). Finally, return the list of unique triplets.

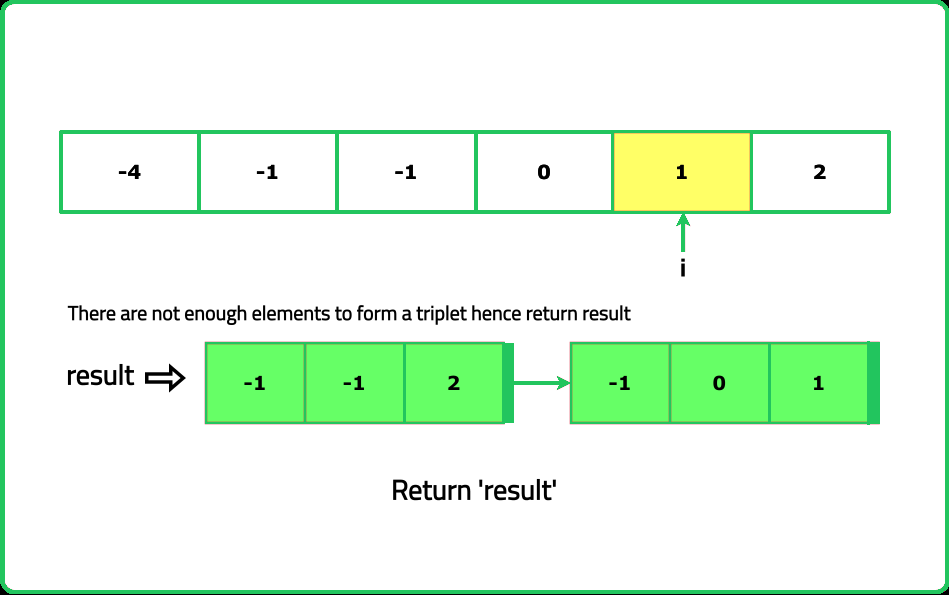
Dry Run

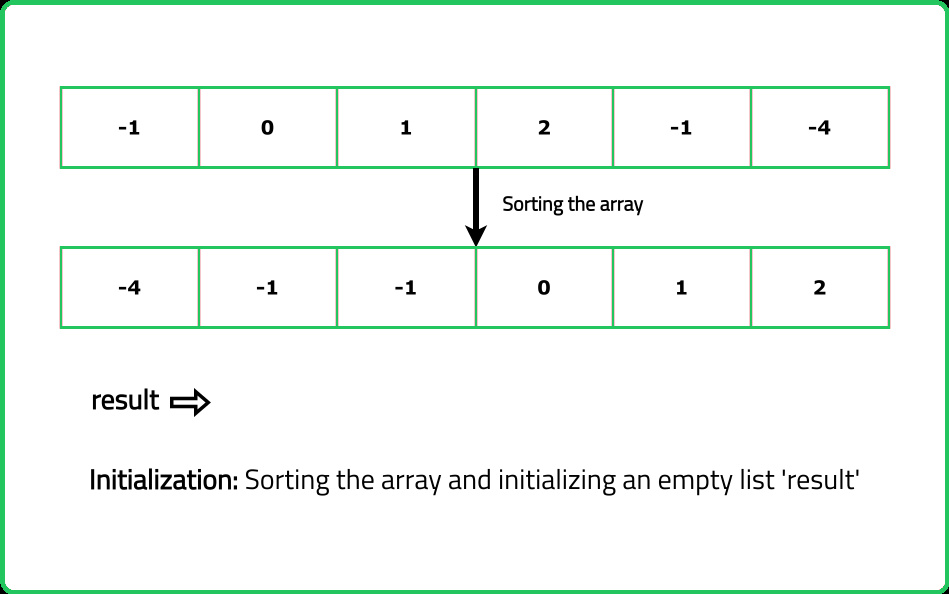
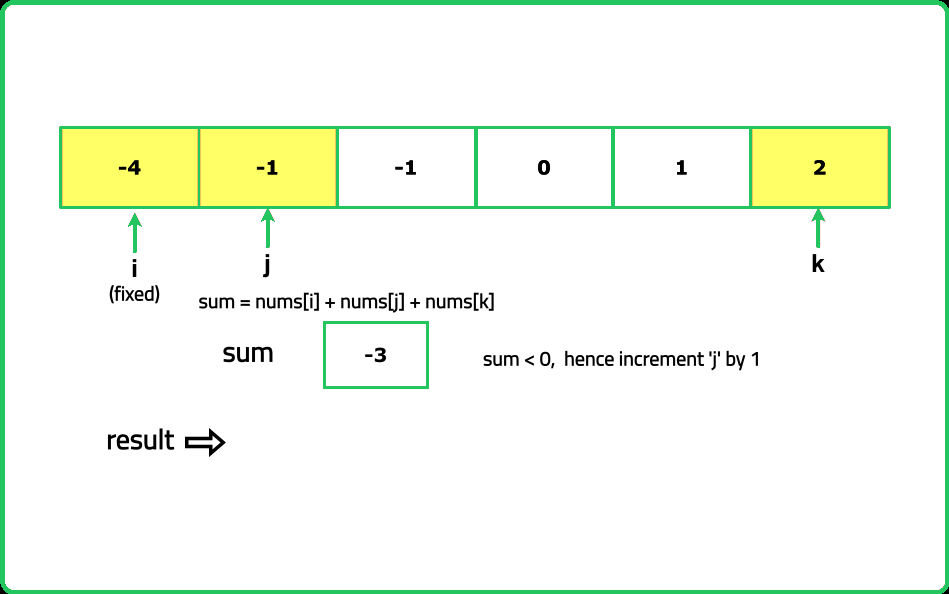
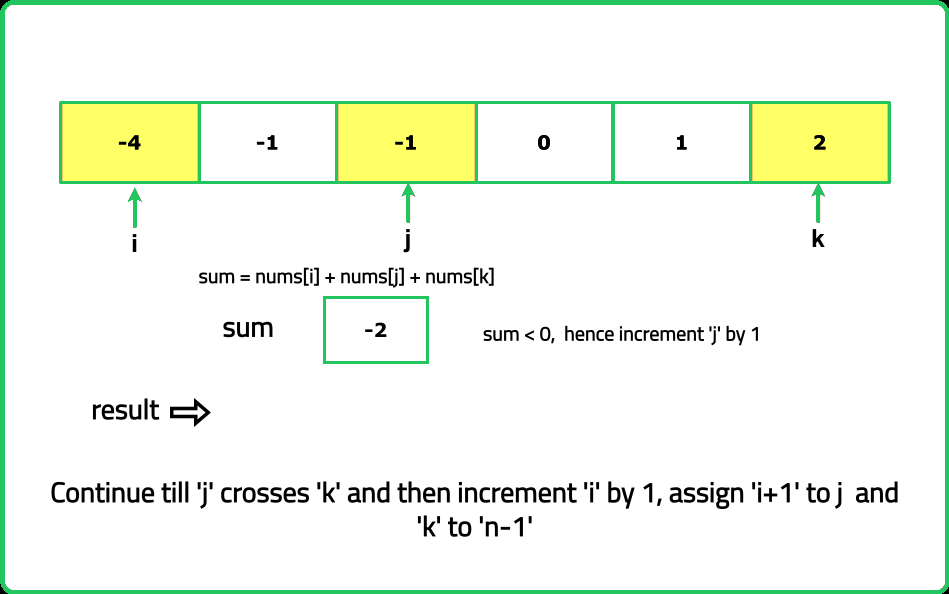
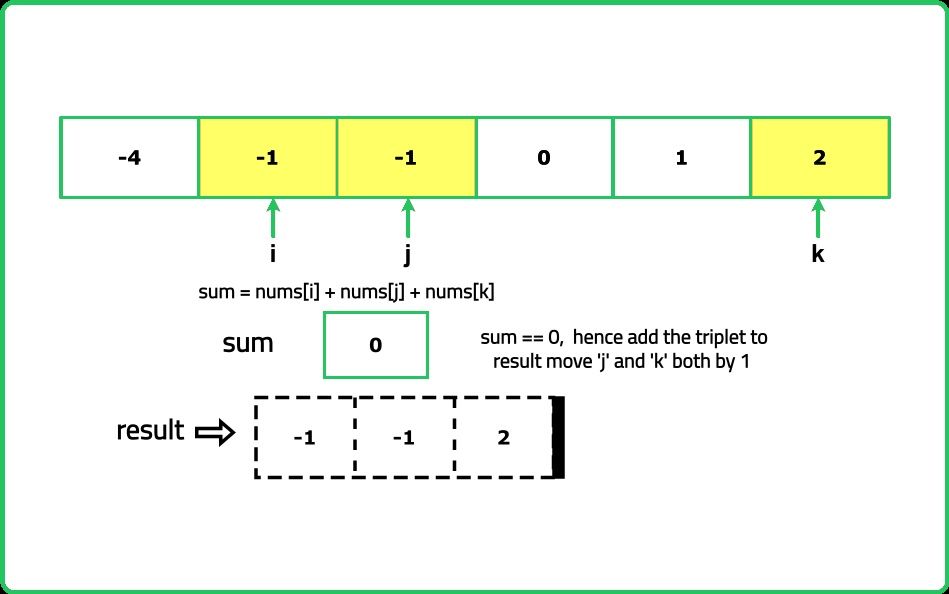
#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to find triplets having sum equals to target
    vector<vector<int>> threeSum(vector<int>& nums) {
        
        // Vector to store the triplets that sum up to target
        vector<vector<int>> ans;
        
        int n = nums.size();
        
        // Sort the input array nums
        sort(nums.begin(), nums.end());
        
        // Iterate through the array to find triplets
        for (int i = 0; i < n; i++) {
            // Skip duplicates
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            
            // Two pointers approach
            int j = i + 1;
            int k = n - 1;
            
            while (j < k) {
                int sum = nums[i] + nums[j] + nums[k];
                
                if (sum < 0) {
                    j++;
                } else if (sum > 0) {
                    k--;
                } else {
                    // Found a triplet that sums up to target
                    vector<int> temp = {nums[i], nums[j], nums[k]};
                    ans.push_back(temp);
                    
                    // Skip duplicates
                    j++;
                    k--;
                    while (j < k && nums[j] == nums[j - 1]) j++;
                    while (j < k && nums[k] == nums[k + 1]) k--;
                }
            }
        }
        
        return ans;
    }
};

int main() {
    vector<int> nums = {-1, 0, 1, 2, -1, -4};
    
    // Create an instance of Solution class
    Solution sol;
    
    vector<vector<int>> ans = sol.threeSum(nums);
    
    // Print the result
    for (auto& triplet : ans) {
        cout << "[";
        for (auto& num : triplet) {
            cout << num << " ";
        }
        cout << "] ";
    }
    cout << "\n";
    
    return 0;
}
import java.util.*;

class Solution {
    // Function to find triplets having sum equals to target
    public List<List<Integer>> threeSum(int[] nums) {
        
        // List to store the triplets that sum up to target
        List<List<Integer>> ans = new ArrayList<>();
        
        int n = nums.length;
        
        // Sort the input array nums
        Arrays.sort(nums);
        
        // Iterate through the array to find triplets
        for (int i = 0; i < n; i++) {
            // Skip duplicates
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            
            // Two pointers approach
            int j = i + 1;
            int k = n - 1;
            
            while (j < k) {
                int sum = nums[i] + nums[j] + nums[k];
                
                if (sum < 0) {
                    j++;
                } else if (sum > 0) {
                    k--;
                } else {
                    // Found a triplet that sums up to target
                    List<Integer> temp = new ArrayList<>();
                    temp.add(nums[i]);
                    temp.add(nums[j]);
                    temp.add(nums[k]);
                    ans.add(temp);
                    
                    // Skip duplicates
                    j++;
                    k--;
                    while (j < k && nums[j] == nums[j - 1]) j++;
                    while (j < k && nums[k] == nums[k + 1]) k--;
                }
            }
        }
        
        return ans;
    }
}

public class Main {
    public static void main(String[] args) {
        int[] nums = {-1, 0, 1, 2, -1, -4};
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        List<List<Integer>> ans = sol.threeSum(nums);
        
        // Print the result
        for (List<Integer> triplet : ans) {
            System.out.print("[");
            for (int num : triplet) {
                System.out.print(num + " ");
            }
            System.out.print("] ");
        }
        System.out.println();
    }
}
from typing import List

class Solution:
    # Function to find triplets having sum equals to target
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        
        # List to store the triplets that sum up to target
        ans = []
        
        n = len(nums)
        
        # Sort the input array nums
        nums.sort()
        
        # Iterate through the array to find triplets
        for i in range(n):
            # Skip duplicates
            if i > 0 and nums[i] == nums[i - 1]:
                continue
            
            # Two pointers approach
            j = i + 1
            k = n - 1
            
            while j < k:
                sum_val = nums[i] + nums[j] + nums[k]
                
                if sum_val < 0:
                    j += 1
                elif sum_val > 0:
                    k -= 1
                else:
                    # Found a triplet that sums up to target
                    temp = [nums[i], nums[j], nums[k]]
                    ans.append(temp)
                    
                    # Skip duplicates
                    j += 1
                    k -= 1
                    while j < k and nums[j] == nums[j - 1]:
                        j += 1
                    while j < k and nums[k] == nums[k + 1]:
                        k -= 1
        
        return ans

if __name__ == "__main__":
    nums = [-1, 0, 1, 2, -1, -4]
    
    # Create an instance of Solution class
    sol = Solution()

    ans = sol.threeSum(nums)
    
    # Print the result
    for triplet in ans:
        print(f"[{', '.join(map(str, triplet))}]")
class Solution {
    // Function to find triplets having sum equals to target
    threeSum(nums) {
        
        // Array to store the triplets that sum up to target
        let ans = [];
        
        // Sort the input array nums
        nums.sort((a, b) => a - b);
        
        let n = nums.length;
        
        // Iterate through the array to find triplets
        for (let i = 0; i < n; i++) {
            // Skip duplicates
            if (i > 0 && nums[i] === nums[i - 1]) continue;
            
            // Two pointers approach
            let j = i + 1;
            let k = n - 1;
            
            while (j < k) {
                let sumVal = nums[i] + nums[j] + nums[k];
                
                if (sumVal < 0) {
                    j++;
                } else if (sumVal > 0) {
                    k--;
                } else {
                    // Found a triplet that sums up to target
                    let temp = [nums[i], nums[j], nums[k]];
                    ans.push(temp);
                    
                    // Skip duplicates
                    j++;
                    k--;
                    while (j < k && nums[j] === nums[j - 1]) j++;
                    while (j < k && nums[k] === nums[k + 1]) k--;
                }
            }
        }
        
        return ans;
    }
}

// Main function to test the Solution class
function main() {
    let nums = [-1, 0, 1, 2, -1, -4];
    
    // Create an instance of Solution class
    let sol = new Solution();

    let ans = sol.threeSum(nums);
    
    // Print the result
    ans.forEach(triplet => {
        console.log(`[${triplet.join(', ')}]`);
    });
}

// Invoke the main function
main();

Complexity Analysis

Time Complexity: O(NlogN)+O(N²), where N is size of the array. As the pointer i, is running for approximately N times. And both the pointers j and k combined can run for approximately N times including the operation of skipping duplicates. So the total time complexity will be O(N²). Space Complexity: O(1), no extra space is used.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Approach

Complexity Analyis

Intuition

Approach

Complexity Analyis

Intuition

Approach

Dry Run

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code

Facts