Maximum Consecutive Ones

Arrays Fundamentals Easy

A fun and practical application of this problem exists in data compression techniques, used in various aspects of software development
In particular, a variant of this problem is employed in Run-Length Encoding (RLE) that is a simple form of data compression where runs of data are stored as a single data value and count
It counts the occurrences of consecutive 1s (or 0s), which is similar to the given problem
RLE is used in graphics files formats including BMP, TIFF, and in certain PDF compression schemes

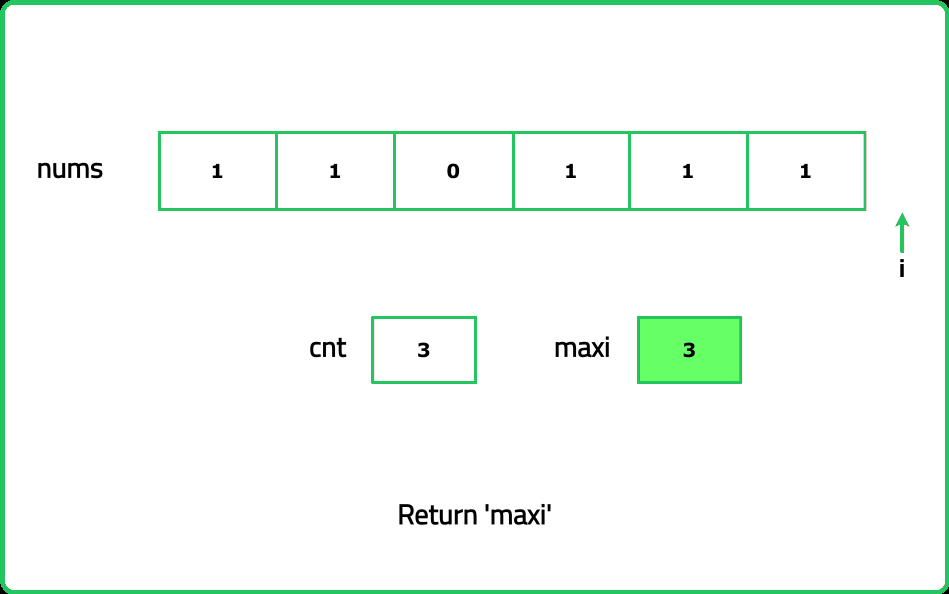
Given a binary array nums, return the maximum number of consecutive 1s in the array.

A binary array is an array that contains only 0s and 1s.

Examples:

Input: nums = [1, 1, 0, 0, 1, 1, 1, 0]

Output: 3

Explanation: The maximum consecutive 1s are present from index 4 to index 6, amounting to 3 1s

Input: nums = [0, 0, 0, 0, 0, 0, 0, 0]

Output: 0

Explanation: No 1s are present in nums, thus we return 0

Input: nums = [1, 0, 1, 1, 1, 0, 1, 1, 1]

Constraints

1 <= nums.length <= 10⁵
nums[i] is either 0 or 1.

Hints

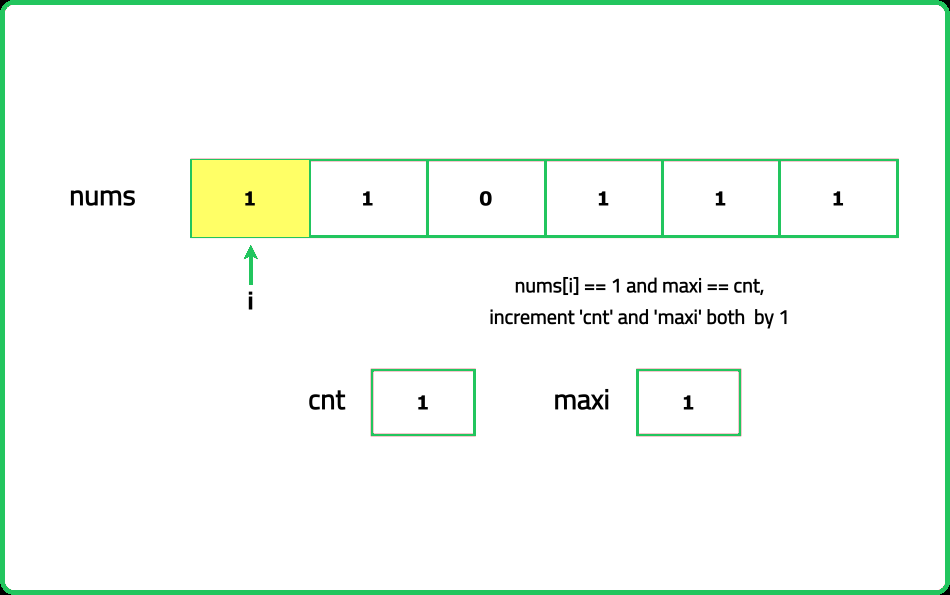
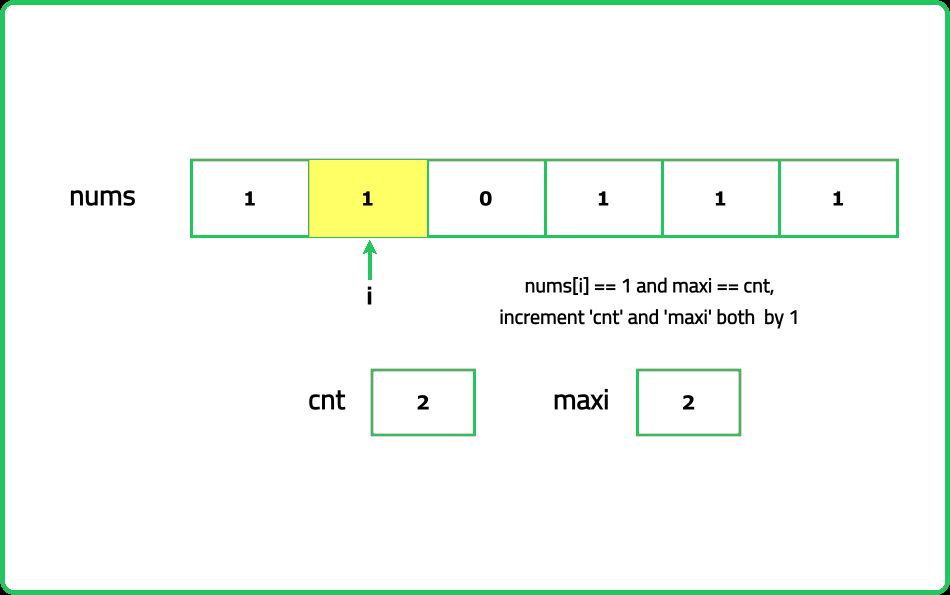
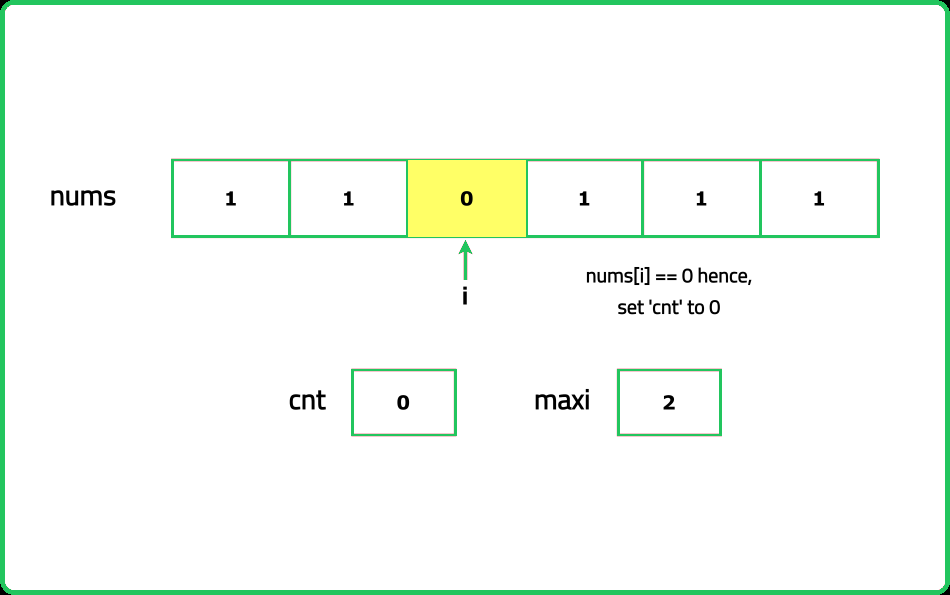
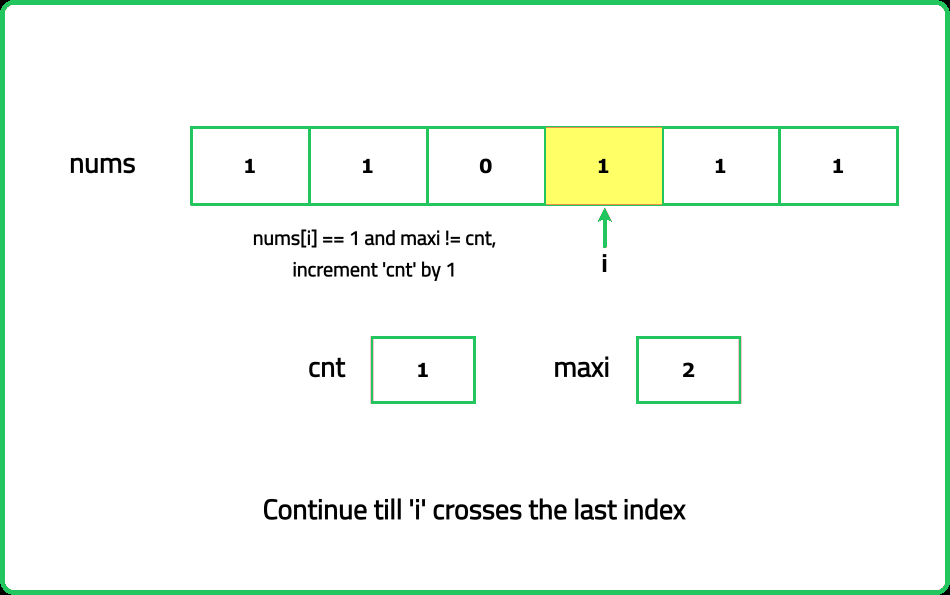
Traverse the array while keeping a running count of consecutive 1s. Reset the count to 0 whenever a 0 is encountered.
Maintain a variable to track the maximum count of consecutive 1s observed during traversal.

Company Tags

Byju's Oracle Mastercard Bain & Company Splunk HashiCorp Reddit Zynga Micron Technology OYO Rooms Roche Activision Blizzard Uber Ernst & Young Nutanix ARM American Express Morgan Stanley Philips Healthcare JPMorgan Chase Pinterest Swiggy Optum Stripe Wayfair TCS Cognizant Accenture Infosys Capgemini Wipro Amazon

Editorial

Intuition

To find the number of maximum consecutive 1s, the idea is to count the number of 1s each time we encounter them and update the maximum number of 1s. On encountering any 0, reset the count to 0 again so as to count the next consecutive 1s.

Approach

Initialize two variables, count and max_count to 0. Traverse the array and if the current element is 1, increment the count by 1.

Update max_count if count is greater than max_count.

If the current element is 0, reset the count variable to 0 and at last return max_count.

Dry Run

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
        /* Initialize count and max_count 
        to track current and maximum consecutive 1s */
        int cnt = 0;
        int maxi = 0;

        // Traverse the vector
        for (int i = 0; i < nums.size(); i++) {

            /* If the current element is 1, 
            increment the count*/
            if (nums[i] == 1) {
                cnt++;

                /* Update maxi if current
                count is greater than maxi*/
                maxi = max(maxi, cnt);

            } else {
                /* If the current element 
               is 0, reset the count*/
                cnt = 0;
            }
        }
        // Return maximum count of consecutive 1s
        return maxi;
    }
};

int main() {
    
    vector nums = {1, 1, 0, 1, 1, 1};

    // Create an instance of the Solution class
    Solution sol;

    int ans = sol.findMaxConsecutiveOnes(nums);

    cout << "The maximum consecutive 1's are " << ans << endl;
    return 0;
}
import java.util.*;

class Solution {
    public int findMaxConsecutiveOnes(int[] nums) {
        /* Initialize count and max_count 
               to track current and maximum consecutive 1s */
        int cnt = 0;
        int maxi = 0;

        // Traverse the array
        for (int i = 0; i < nums.length; i++) {

            // If the current element is 1, increment the count
            if (nums[i] == 1) {
                cnt++;

                // Update maxi if current count is greater than maxi
                maxi = Math.max(maxi, cnt);

            } else {
                // If the current element is 0, reset the count
                cnt = 0;
            }
        }
        // Return the maximum count of consecutive 1s
        return maxi;
    }

    public static void main(String[] args) {
     
        int[] nums = {1, 1, 0, 1, 1, 1};

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Find and print the maximum consecutive 1s
        int ans = sol.findMaxConsecutiveOnes(nums);
        System.out.println("The maximum consecutive 1's are " + ans);
    }
}
from typing import List

class Solution:
    def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
        ''' Initialize count and max_count 
              to track current and maximum consecutive 1s '''
        cnt = 0
        maxi = 0

        # Traverse the array
        for num in nums:
            # If the current element is 1, increment the count
            if num == 1:
                cnt += 1

                # Update maxi if current count is greater than maxi
                maxi = max(maxi, cnt)

            else:
                # If the current element is 0, reset the count
                cnt = 0

        # Return the maximum count of consecutive 1s
        return maxi

# Main function
if __name__ == "__main__":
   
    nums = [1, 1, 0, 1, 1, 1]

    # Create an instance of the Solution class
    sol = Solution()

    # Find and print the maximum consecutive 1s
    ans = sol.findMaxConsecutiveOnes(nums)
    print("The maximum consecutive 1's are", ans)
class Solution {
    findMaxConsecutiveOnes(nums) {
        /* Initialize count and max_count 
              to track current and maximum consecutive 1s */
        let cnt = 0;
        let maxi = 0;

        // Traverse the array
        for (let i = 0; i < nums.length; i++) {

            /*If the current element is 
           1, increment the count*/
            if (nums[i] == 1) {
                cnt++;

                /*Update maxi if current 
               count is greater than maxi*/
                maxi = Math.max(maxi, cnt);

            } else {
                // If the current element is 0, reset the count
                cnt = 0;
            }
        }

        // Return the maximum count of consecutive 1s
        return maxi;
    }
}

const nums = [1, 1, 0, 1, 1, 1];

// Create an instance of the Solution class
const sol = new Solution();

// Find and print the maximum consecutive 1s
const ans = sol.findMaxConsecutiveOnes(nums);
console.log("The maximum consecutive 1's are " + ans);

Complexity Analysis

Time Complexity: O(N), as there is single traversal of the array .Here N is the number of elements in the array.
Space Complexity: O(1), as no additional space is used .

Code

Problem List