House robber

Here, the problem is asking for maximum money the theif can rob, so based on the discussion in previous articles, it is obvious that we think of recursion to solve this problem.

This problem can be tackled using the method outlined in the article on Maximum Sum of non-adjacent elements. It is strongly recommended that readers review that article before proceeding with this one.

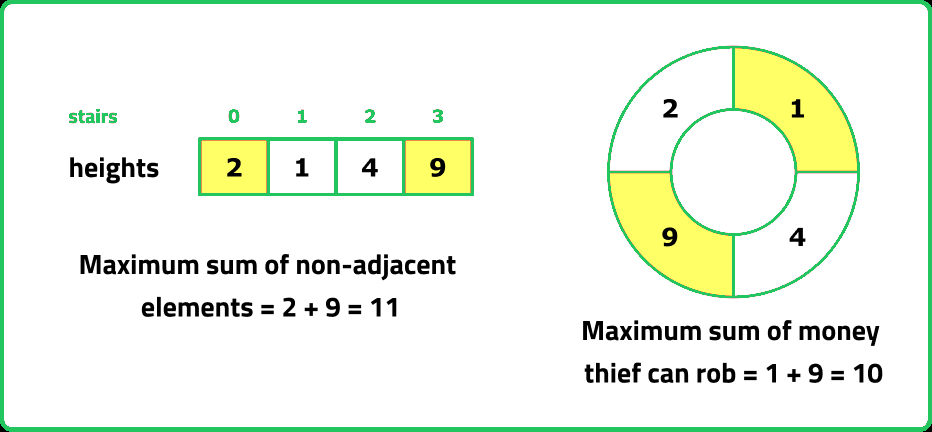
According to the article on maximum sum of non-adjacent elements, the answer will be 4 (2+2) since the maximum sum of non-adjacent elements is being considered.

As this problem states that the houses are arranged in circular manner, it means the first and last houses are also adjacent to each other. So, the maximum possible answer in this question can be 3.

Modification to the article on maximum sum of non-adjacent elements:

In previous questions, the focus was on finding the maximum sum of non-adjacent elements. As the arrangement was linear, the first and last elements were not adjacent to each other. In this case of a circular street where the first and last houses are adjacent, it is certain that both cannot be included in the answer simultaneously, as they are adjacent to each other.

Building upon the previous Article, it can be inferred that the last element may not be included in the optimal solution. In such a scenario, the first element could be considered instead. This resultant answer is denoted as ans1. Therefore, the array is reduced by excluding the last element, forming arr1, and applying the previous approach to find ans1.

It is also possible that the final answer includes the last element. In this case, the first element cannot be included (due to adjacency). The same approach is applied to the reduced array (arr - first element), denoted as arr2, to determine the answer, referred to as ans2.

The final answer can either be ans1 or ans2. To determine the maximum money robbed by the robber, max(ans1, ans2) is returned as the final answer.

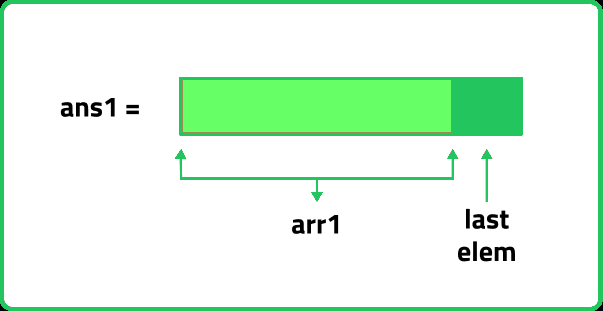
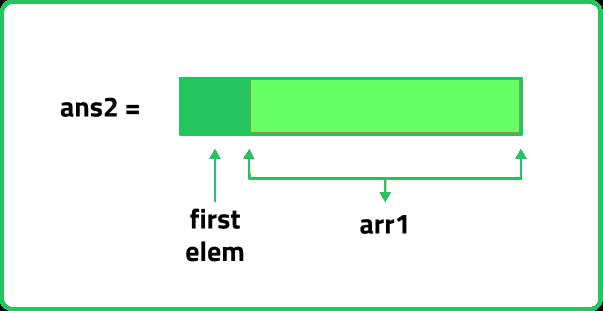
Approach to solving the problem:

Make two reduced arrays: arr1, it has every element except the last one(arr-last element) and arr2, it has every element except the first one(arr-first element). As the first and the last element can't be considered simultaneously in case of circular arrangement.

Find the sum of maximum of non-adjacent elements: In arr1 and arr2 separately find the maximum sum by using the pick/non-pick method used in previous article. Let’s call the answers we got ans1 and ans2 respectively.

Return max(ans1, ans2) as our final answer, as the answer requires maximum money.

Steps to form recursive solution:

Represent the function in terms of indices: As the houses are arranged in circular manner, each house can be represented as an index. f(n-1) will return the maximum sum from 0th index till (n-1)th index. Here two seperate arrays will be considered and all the following steps will be applied on both of them.

Try all the choices to reach the goal: As mentioned earlier we will use the pick/non-pick technique to generate all subsequences. In addition to that only pick up the non-adjacent elements in this step.

There are two possible choices that can be made for each index. If we pick an element then, pick = arr[ind] + f(ind-2). The reason we are doing f(ind-2) is because we have picked the current index(ind) element so we need to pick a non-adjacent element so we choose the index ‘ind-2’ instead of ‘ind-1’.

The other chice can be to ignore the current element at index(ind) in our subsequence. So nonPick= 0 + f(ind-1). As we don’t pick the current element, we can consider the adjacent element in the subsequence.

/*It is pseudocode and it is not tied to 
any specific programming language*/
f(ind, arr[]){
    //base condition
    pick = arr[ind] + find(ind-2, arr)
    notPick = 0 + f(ind-1, arr)
}

Take the maximum of all the choices: As the problem statement asks to find the maximum sum, return the maximum of two choices made in the above step.

/*It is pseudocode and it is not tied to
 any specific programming language*/
f(ind, arr[]){
    //base condition
    pick = arr[ind] + f(ind-2, arr)
    notPick = 0 + f(ind - 1, arr)
    return max(pick, notPick)
}

Base Conditions: If ind=0, then we know to reach at index=0, we would have ignored the element at index = 1. Therefore, we can simply return the value of arr[ind] and consider it in the subsequence. If ind<0, this case can hit when we call f(ind-2) at ind=1. In this case we want to return to the calling function so we simply return 0 so that nothing is added to the subsequence sum.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using recursion
    int func(int ind, vector<int> &arr){
        
        //Base case
        if (ind == 0) 
            return arr[ind];
        if (ind < 0)  
            return 0;

        // Choosing the current element
        int pick = arr[ind] + func(ind - 2, arr);  
    
        // Skipping the current element
        int nonPick = 0 + func(ind - 1, arr);  

        // Return the maximum 
        return max(pick, nonPick);
    }
public:
    //Function to find the maximum money robber can rob
    int houseRobber(vector<int>& money) {
        int n = money.size();
        vector<int> arr1;
        vector<int> arr2;
       
        //If array has only one element, return that
        if(n==1)
           return money[0];
        
        for(int i=0; i<n; i++){
            /*Store every element in 
            arr1 except the last element*/
            if(i!=n-1) arr1.push_back(money[i]);
            
            /*Store every element in 
            arr2 except the first element*/
            if(i!=0) arr2.push_back(money[i]);
        }
    
        int ans1 = func(arr1.size()-1, arr1);
        int ans2 = func(arr2.size()-1, arr2);
    
        //Return the maximum of an1 and ans2
        return max(ans1,ans2);
    }
};

int main(){
    vector<int> arr{1,5,1,2,6};
 
    //Create an  instance of Solution class
    Solution sol;
    
    //Print the solution
    cout<<sol.houseRobber(arr);
}
import java.util.*;

class Solution {
    // Recursive function to calculate the maximum money robbed
    private int func(int ind, int[] arr) {
        // Base cases
        if (ind == 0) {
            return arr[ind];
        }
        if (ind < 0) {
            return 0;
        }

        // Choosing the current element
        int pick = arr[ind] + func(ind - 2, arr);

        // Skipping the current element
        int nonPick = 0 + func(ind - 1, arr);

        // Return the maximum
        return Math.max(pick, nonPick);
    }

    // Function to find the maximum money robber can rob
    public int houseRobber(int[] money) {
        int n = money.length;
        int[] arr1, arr2;

        // If array has only one element, return that
        if (n == 1)
            return money[0];

        // Create arr1 (excluding last element)
        arr1 = new int[n - 1];
        for (int i = 0; i < n - 1; i++) {
            arr1[i] = money[i];
        }

        // Create arr2 (excluding first element)
        arr2 = new int[n - 1];
        for (int i = 1; i < n; i++) {
            arr2[i - 1] = money[i];
        }

        int ans1 = func(arr1.length - 1, arr1);
        int ans2 = func(arr2.length - 1, arr2);

        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }

    public static void main(String[] args) {
        int[] arr = {1, 5, 1, 2, 6};

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the solution
        System.out.println(sol.houseRobber(arr));
    }
}
class Solution:
    #Function to solve the problem using recursion
    def func(self, ind, arr):
        # Base cases
        if ind == 0:
            return arr[ind]
        if ind < 0:
            return 0
        
        # Choosing the current element
        pick = arr[ind] + self.func(ind - 2, arr)
        
        # Skipping the current element
        nonPick = 0 + self.func(ind - 1, arr)
        
        # Return the maximum
        return max(pick, nonPick)
    
    def houseRobber(self, money):
        n = len(money)
        arr1 = []
        arr2 = []
        
        # If array has only one element, return that
        if n == 1:
            return money[0]
        
        for i in range(n):
            """ Store every element in 
            arr1 except the last element"""
            if i != n - 1:
                arr1.append(money[i])
                
            """ Store every element in 
            arr2 except the first element"""
            if i != 0:
                arr2.append(money[i])
        
        ans1 = self.func(len(arr1) - 1, arr1)
        ans2 = self.func(len(arr2) - 1, arr2)
        
        # Return the maximum of ans1 and ans2
        return max(ans1, ans2)

arr = [1, 5, 1, 2, 6]

#Create an instance of Solution class
sol = Solution()

print(sol.houseRobber(arr))
class Solution {
    //Function to solve the problem using recursion
    func(ind, arr) {
        // Base cases
        if (ind === 0) {
            return arr[ind];
        }
        if (ind < 0) {
            return 0;
        }
        
        // Choosing the current element
        let pick = arr[ind] + this.func(ind - 2, arr);
        
        // Skipping the current element
        let nonPick = 0 + this.func(ind - 1, arr);
        
        // Return the maximum
        return Math.max(pick, nonPick);
    }
    
    houseRobber(money) {
        let n = money.length;
        let arr1 = [];
        let arr2 = [];
        
        // If array has only one element, return that
        if (n === 1) {
            return money[0];
        }
        
        for (let i = 0; i < n; i++) {
            /* Store every element in 
            arr1 except the last element*/
            if (i !== n - 1) {
                arr1.push(money[i]);
            }
            
            /* Store every element in arr2
            except the first element*/
            if (i !== 0) {
                arr2.push(money[i]);
            }
        }
        
        let ans1 = this.func(arr1.length - 1, arr1);
        let ans2 = this.func(arr2.length - 1, arr2);
        
        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }
}

let arr = [1, 5, 1, 2, 6];

//Create an instance of Solution class
let sol = new Solution();

console.log(sol.houseRobber(arr));

Complexity Analysis:

Time Complexity: O(2^N) + O(2^N), where N is the given size of array. This is because each call branches into two more calls, leading to an exponential growth in the number of calls and the recursive function is being called twice.

Space Complexity:O(N) + O(N) + O(N) + O(N). As two additional array is being used and an extra O(N) + O(N) because the maximum depth of the recursion stack can go up to N, and the function is being called twice.

If we observe the recursion tree, we will observe a number of overlapping subproblems. Therefore the recursive solution can be memoized to reduce the time complexity.

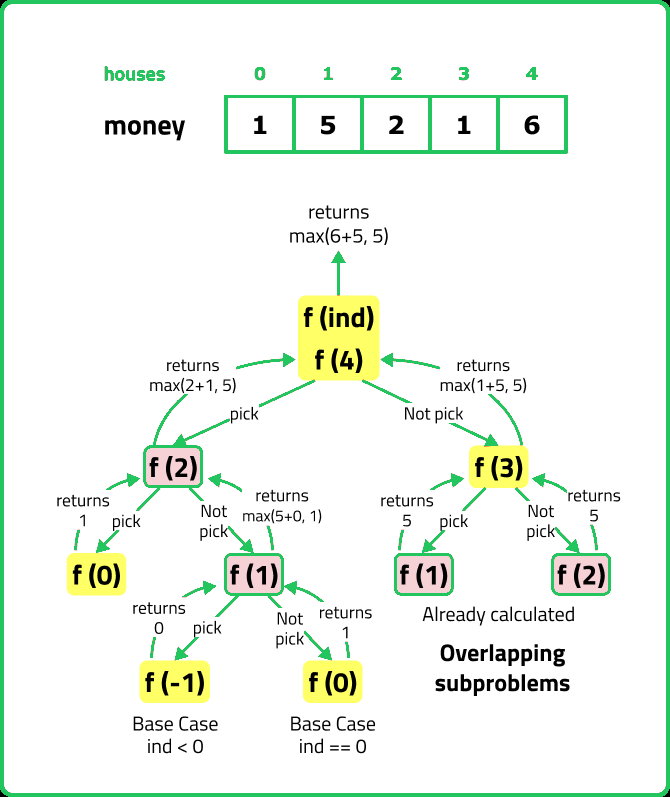
Steps to convert Recursive code to memoization solution:

Declare an Array dp[] of Size n: Here, n is the size of the given array in the problem, as the highest number of subproblems can be n(including 0 as well). It represents the solution to the subproblem for any given index. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using recursion
    int func(int ind, vector<int> &arr, vector<int> &dp){
        
        //Base case
        if (ind == 0) 
            return arr[ind];
        if (ind < 0)  
            return 0;

        if(dp[ind] != -1){
            return dp[ind];
        }
        // Choosing the current element
        int pick = arr[ind] + func(ind - 2, arr, dp);  
    
        // Skipping the current element
        int nonPick = 0 + func(ind - 1, arr, dp);  

        /* Store the result in dp 
        array and return the maximum */
        return dp[ind] = max(pick, nonPick);
    }
public:
    //Function to find the maximum money robber can rob
    int houseRobber(vector<int>& money) {
        int n = money.size();
        vector<int> arr1;
        vector<int> arr2;
       
        //If array has only one element, return that
        if(n==1)
           return money[0];
        
        for(int i=0; i<n; i++){
            /*Store every element in 
            arr1 except the last element*/
            if(i!=n-1) arr1.push_back(money[i]);
            
            /*Store every element in 
            arr2 except the first element*/
            if(i!=0) arr2.push_back(money[i]);
        }
        
        //Initialize the dp array with -1
        vector<int> dp(n, -1);
        int ans1 = func(arr1.size()-1, arr1, dp);
        
        vector<int> dp1(n, -1);
        int ans2 = func(arr2.size()-1, arr2, dp1);
    
        //Return the maximum of an1 and ans2
        return max(ans1,ans2);
    }
};

int main(){
    vector<int> arr{1,5,1,2,6};
 
    //Create an  instance of Solution class
    Solution sol;
    
    //Print the solution
    cout<<sol.houseRobber(arr);
}
import java.util.*;

class Solution {
    // Function to solve the problem using memoization
    private int func(int ind, int[] arr, int[] dp) {
        // Base cases
        if (ind == 0)
            return arr[ind];
        if (ind < 0)
            return 0;

        // If dp[ind] already has a value, return it
        if (dp[ind] != -1) {
            return dp[ind];
        }

        // Choosing the current element
        int pick = arr[ind] + func(ind - 2, arr, dp);

        // Skipping the current element
        int nonPick = func(ind - 1, arr, dp);

        /* Store the result in dp 
        array and return the maximum*/
        return dp[ind] = Math.max(pick, nonPick);
    }

    // Function to find the maximum money robber can rob
    public int houseRobber(int[] money) {
        int n = money.length;
        if (n == 0)
            return 0;
        if (n == 1)
            return money[0];

        int[] arr1 = new int[n - 1];
        int[] arr2 = new int[n - 1];

        // Populate arr1 and arr2
        for (int i = 0; i < n; i++) {
            if (i != n - 1)
                arr1[i] = money[i];
            if (i != 0)
                arr2[i - 1] = money[i];
        }

        // Initialize the dp arrays with -1
        int[] dp1 = new int[n];
        Arrays.fill(dp1, -1);
        int ans1 = func(arr1.length - 1, arr1, dp1);

        int[] dp2 = new int[n];
        Arrays.fill(dp2, -1);
        int ans2 = func(arr2.length - 1, arr2, dp2);

        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }

    public static void main(String[] args) {
        int[] arr = {1, 5, 1, 2, 6};
        
        //Create an instance of Solution class
        Solution sol = new Solution();
        
        System.out.println(sol.houseRobber(arr));
    }
}
class Solution:
    #Function to solve the problem using memoization
    def func(self, ind, arr, dp):
        # Base cases
        if ind == 0:
            return arr[ind]
        if ind < 0:
            return 0
        
        # If dp[ind] already has a value, return it
        if dp[ind] != -1:
            return dp[ind]
        
        # Choosing the current element
        pick = arr[ind] + self.func(ind - 2, arr, dp)
        
        # Skipping the current element
        nonPick = self.func(ind - 1, arr, dp)
        
        """ Store the result in dp 
        array and return the maximum"""
        dp[ind] = max(pick, nonPick)
        return dp[ind]
    
    def houseRobber(self, money):
        n = len(money)
        if n == 0:
            return 0
        if n == 1:
            return money[0]
        
        # Exclude last element
        arr1 = money[:-1] 
        
        # Exclude first element
        arr2 = money[1:]   
        
        # Initialize the dp arrays with -1
        dp1 = [-1] * n
        ans1 = self.func(len(arr1) - 1, arr1, dp1)
        
        dp2 = [-1] * n
        ans2 = self.func(len(arr2) - 1, arr2, dp2)
        
        # Return the maximum of ans1 and ans2
        return max(ans1, ans2)

arr = [1, 5, 1, 2, 6]

#Create an instance of Solution class
sol = Solution()

print(sol.houseRobber(arr))
class Solution {
    /* Function to solve the problem 
    using with memoization*/
    func(ind, arr, dp) {
        // Base cases
        if (ind === 0)
            return arr[ind];
        if (ind < 0)
            return 0;

        // If dp[ind] already has a value, return it
        if (dp[ind] !== -1) {
            return dp[ind];
        }

        // Choosing the current element
        let pick = arr[ind] + this.func(ind - 2, arr, dp);

        // Skipping the current element
        let nonPick = this.func(ind - 1, arr, dp);

        /* Store the result in dp 
        array and return the maximum*/
        dp[ind] = Math.max(pick, nonPick);
        return dp[ind];
    }

    // Function to find the maximum money robber can rob
    houseRobber(money) {
        let n = money.length;
        if (n === 0)
            return 0;
        if (n === 1)
            return money[0];

        // Exclude last element
        let arr1 = money.slice(0, n - 1);  
        
        // Exclude first element
        let arr2 = money.slice(1);         
        
        // Initialize the dp arrays with -1
        let dp1 = new Array(n).fill(-1);
        let ans1 = this.func(arr1.length - 1, arr1, dp1);

        let dp2 = new Array(n).fill(-1);
        let ans2 = this.func(arr2.length - 1, arr2, dp2);

        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }
}

let arr = [1, 5, 1, 2, 6];

//Create an instance of Solution class
let sol = new Solution();

console.log(sol.houseRobber(arr));

Complexity Analysis:

Time Complexity: O(N) + O(N), where N is the given size of array. The overlapping subproblems will return the answer in constant time O(1). As total subproblems can be at max N. Therefore it will take O(N) and the function is being called twice.

Space Complexity:O(N) + O(N) + O(N) + O(N) + O(N) + O(N), Two arrays to store the elements seperately are being used. Additionaly, two dp arrays and stack space of O(N) is used for two function calls. Therefore the overall space complexity will be ≈ O(N).

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare an Array dp[] of Size n: Here, n is the size of the array provided as input. It represents the solution to the subproblem for any given index.

Setting Base Cases in the Array: In the recursive code, we knew the answer for base case, when 'ind' = 0, Here, dp[0] is initialized directly to arr[0] because if there is only one element in the array, that element itself is the maximum sum.

Iterative Computation Using a Loop: Set an iterative loop that traverses the array( from index 1 to n-1). To compute the solution for larger values, use a loop that iterates from the smallest subproblem up to n-1.

Explanation of dp[i] Calculation: The current value(dp[i]) represents the subproblem and by the recurrence relation it is obvious that dp[i] is calculated by either picking the current element or not picking it (dp[i-2] + arr[i] and dp[i-1]))

Choosing the maximum: Update dp[i] to store the maximum of these two values pick and nonPick.

Returning the last element: The last element of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using tabulation
    int func(vector<int> &nums){
        int ind = nums.size();
        vector<int> dp(ind, 0);
        
        // Base case
        dp[0] = nums[0];

        // Iterate through the elements of the array
        for (int i = 1; i < ind; i++) {
            
            /* Calculate maximum value by either picking
            the current element or not picking it*/
            int pick = nums[i];
            if (i > 1)
                pick += dp[i - 2];
            int nonPick = dp[i - 1];

            // Store the maximum value in dp array
            dp[i] = max(pick, nonPick);
        }

        /* The last element of the dp array
        will contain the maximum sum*/
        return dp[ind-1];
    }
public:
    //Function to find the maximum money robber can rob
    int houseRobber(vector<int>& money) {
        int n = money.size();
        vector<int> arr1;
        vector<int> arr2;
       
        //If array has only one element, return that
        if(n==1)
           return money[0];
        
        for(int i=0; i<n; i++){
            /*Store every element in 
            arr1 except the last element*/
            if(i!=n-1) arr1.push_back(money[i]);
            
            /*Store every element in 
            arr2 except the first element*/
            if(i!=0) arr2.push_back(money[i]);
        }
        int ans1 = func(arr1);
        
        int ans2 = func(arr2);
    
        //Return the maximum of an1 and ans2
        return max(ans1,ans2);
    }
};

int main(){
    vector<int> arr{1,5,1,2,6};
 
    //Create an  instance of Solution class
    Solution sol;
    
    //Print the solution
    cout<<sol.houseRobber(arr);
}
import java.util.*;

class Solution {
    // Function to solve the problem using memoization
    private int func(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        
        // Base case
        dp[0] = nums[0];

        // Iterate through the elements of the array
        for (int i = 1; i < n; i++) {
            
            /* Calculate maximum value by either picking
            the current element or not picking it */
            int pick = nums[i];
            if (i > 1)
                pick += dp[i - 2];
            int nonPick = dp[i - 1];

            // Store the maximum value in dp array
            dp[i] = Math.max(pick, nonPick);
        }

        /* The last element of the dp array
        will contain the maximum sum */
        return dp[n - 1];
    }

    // Function to find the maximum money robber can rob
    public int houseRobber(int[] money) {
        int n = money.length;
        if (n == 0)
            return 0;
        if (n == 1)
            return money[0];

        int[] arr1 = new int[n - 1];
        int[] arr2 = new int[n - 1];

        // Populate arr1 and arr2
        for (int i = 0; i < n; i++) {
            if (i != n - 1)
                arr1[i] = money[i];
            if (i != 0)
                arr2[i - 1] = money[i];
        }
        int ans1 = func(arr1);

        int ans2 = func(arr2);

        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }

    public static void main(String[] args) {
        int[] arr = {1, 5, 1, 2, 6};
        
        //Create an instance of Solution class
        Solution sol = new Solution();
        
        System.out.println(sol.houseRobber(arr));
    }
}
class Solution:
    #Function to solve the problem using tabulation
    def func(self, nums):
        n = len(nums)
        dp = [0] * n
        
        # Base case
        dp[0] = nums[0]

        # Iterate through the elements of the array
        for i in range(1, n):
            
            """ Calculate maximum value by either picking
            the current element or not picking it"""
            pick = nums[i]
            if i > 1:
                pick += dp[i - 2]
            nonPick = dp[i - 1]

            # Store the maximum value in dp array
            dp[i] = max(pick, nonPick)

        """ The last element of the dp array
        will contain the maximum sum"""
        return dp[-1]
    
    def houseRobber(self, money):
        n = len(money)
        if n == 0:
            return 0
        if n == 1:
            return money[0]
        
        # Exclude last element
        arr1 = money[:-1] 
        
        # Exclude first element
        arr2 = money[1:]   
        
        ans1 = self.func(arr1)
        ans2 = self.func(arr2)
        
        # Return the maximum of ans1 and ans2
        return max(ans1, ans2)

arr = [1, 5, 1, 2, 6]

#Create an instance of Solution class
sol = Solution()

print(sol.houseRobber(arr))
class Solution {
    /* Function to solve the problem 
    using with memoization*/
    func(nums) {
        let n = nums.length;
        let dp = new Array(n).fill(0);
        
        // Base case
        dp[0] = nums[0];

        // Iterate through the elements of the array
        for (let i = 1; i < n; i++) {
            
            /* Calculate maximum value by either picking
            the current element or not picking it*/
            let pick = nums[i];
            if (i > 1)
                pick += dp[i - 2];
            let nonPick = dp[i - 1];

            // Store the maximum value in dp array
            dp[i] = Math.max(pick, nonPick);
        }

        /* The last element of the dp array
        will contain the maximum sum*/
        return dp[n - 1];
    }

    // Function to find the maximum money robber can rob
    houseRobber(money) {
        let n = money.length;
        if (n === 0)
            return 0;
        if (n === 1)
            return money[0];

        // Exclude last element
        let arr1 = money.slice(0, n - 1);  
        
        // Exclude first element
        let arr2 = money.slice(1);         
        
        let ans1 = this.func(arr1);
        let ans2 = this.func(arr2);

        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }
}

let arr = [1, 5, 1, 2, 6];

//Create an instance of Solution class
let sol = new Solution();

console.log(sol.houseRobber(arr));

Complexity Analysis:

Time Complexity: O(N)+O(N), where N is the given size of array. As each element of the array is processed exactly once in a single pass and the function is being called twice.

Space Complexity:O(N)+O(N)+O(N)+O(N), As two arrays are used to store elements. O(N)+O(N), an additional dp array is used, which stores results for each element of the array and function is being called twice. So overall time complexity will be O(N).

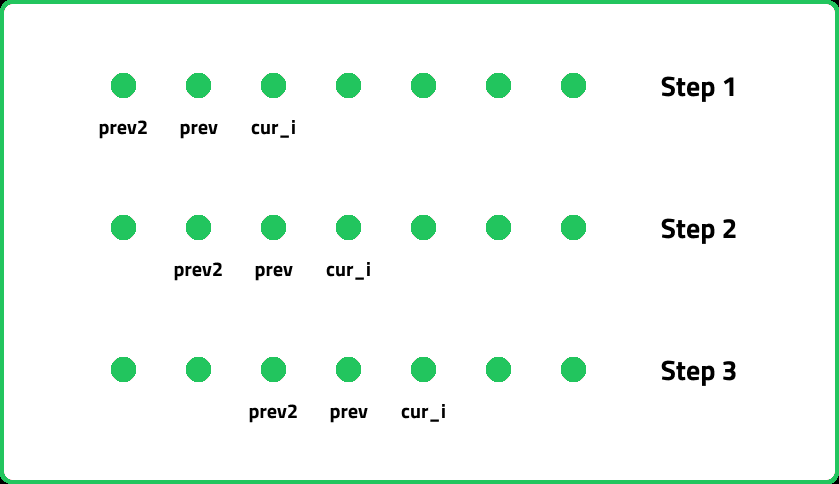
If we do some observation, we find that the values required at every iteration for dp[i] are dp[i-1] and dp[i-2]. we see that for any i, we do need only the last two values in the array. So is there is no need to maintain a whole array for it.

Let us call dp[i-1] as prev and dp[i-2] as prev2. Now understand the following illustration:

Each iteration cur_i and prev become the next iteration’s prev and prev2 respectively. Therefore after calculating cur_i, if we update prev and prev2 according to the next step, we will always get the answer.

After the iterative loop has ended we can simply return prev as our answer. As at the end of the loop prev will contain curr_i, the maximum sum.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to solve the problem using tabulation
    int func(vector<int> &nums){
        int n = nums.size();
        int prev = nums[0];   
        int prev2 = 0;       
    
        for (int i = 1; i < n; i++) {
            // Maximum sum if we pick current element
            int pick = nums[i];  
            
            if (i > 1){
                //Add the maximum sum two elements ago
                pick += prev2;  
            }
            // Maximum sum if we don't pick current element
            int nonPick = 0 + prev;  
            
            // Maximum at the current element
            int cur_i = max(pick, nonPick); 
            
            prev2 = prev;   
            prev = cur_i;    
        }
        // Return the maximum sum
        return prev;  
    }
public:
    //Function to find the maximum money robber can rob
    int houseRobber(vector<int>& money) {
        int n = money.size();
        vector<int> arr1;
        vector<int> arr2;
       
        //If array has only one element, return that
        if(n==1)
           return money[0];
        
        for(int i=0; i<n; i++){
            /*Store every element in 
            arr1 except the last element*/
            if(i!=n-1) arr1.push_back(money[i]);
            
            /*Store every element in 
            arr2 except the first element*/
            if(i!=0) arr2.push_back(money[i]);
        }
        int ans1 = func(arr1);
        
        int ans2 = func(arr2);
    
        //Return the maximum of an1 and ans2
        return max(ans1,ans2);
    }
};

int main(){
    vector<int> arr{1,5,1,2,6};
 
    //Create an  instance of Solution class
    Solution sol;
    
    //Print the solution
    cout<<sol.houseRobber(arr);
}
import java.util.*;

class Solution {
    // Function to solve the problem using memoization
    private int func(int[] nums) {
        int n = nums.length;
        int prev = nums[0];
        int prev2 = 0;

        for (int i = 1; i < n; i++) {
            // Maximum sum if we pick current element
            int pick = nums[i];
            
            if (i > 1) {
                // Add the maximum sum two elements ago
                pick += prev2;
            }
            // Maximum sum if we don't pick current element
            int nonPick = 0 + prev;

            // Maximum at the current element
            int cur_i = Math.max(pick, nonPick);

            prev2 = prev;
            prev = cur_i;
        }
        // Return the maximum sum
        return prev;
    }

    // Function to find the maximum money robber can rob
    public int houseRobber(int[] money) {
        int n = money.length;
        if (n == 0)
            return 0;
        if (n == 1)
            return money[0];

        int[] arr1 = new int[n - 1];
        int[] arr2 = new int[n - 1];

        // Populate arr1 and arr2
        for (int i = 0; i < n; i++) {
            if (i != n - 1)
                arr1[i] = money[i];
            if (i != 0)
                arr2[i - 1] = money[i];
        }
        int ans1 = func(arr1);

        int ans2 = func(arr2);

        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }

    public static void main(String[] args) {
        int[] arr = {1, 5, 1, 2, 6};
        
        //Create an instance of Solution class
        Solution sol = new Solution();
        
        System.out.println(sol.houseRobber(arr));
    }
}
class Solution:
    #Function to solve the problem using tabulation
    def func(self, nums):
        n = len(nums)
        prev = nums[0]
        prev2 = 0

        for i in range(1, n):
            # Maximum sum if we pick current element
            pick = nums[i]

            if i > 1:
                # Add the maximum sum two elements ago
                pick += prev2
            # Maximum sum if we don't pick current element
            nonPick = 0 + prev

            # Maximum at the current element
            cur_i = max(pick, nonPick)

            prev2 = prev
            prev = cur_i

        # Return the maximum sum
        return prev
    
    def houseRobber(self, money):
        n = len(money)
        if n == 0:
            return 0
        if n == 1:
            return money[0]
        
        # Exclude last element
        arr1 = money[:-1] 
        
        # Exclude first element
        arr2 = money[1:]   
        
        ans1 = self.func(arr1)
        ans2 = self.func(arr2)
        
        # Return the maximum of ans1 and ans2
        return max(ans1, ans2)

arr = [1, 5, 1, 2, 6]

#Create an instance of Solution class
sol = Solution()

print(sol.houseRobber(arr))
class Solution {
    /* Function to solve the problem 
    using with memoization*/
    func(nums) {
        let n = nums.length;
        let prev = nums[0];
        let prev2 = 0;

        for (let i = 1; i < n; i++) {
            // Maximum sum if we pick current element
            let pick = nums[i];

            if (i > 1) {
                // Add the maximum sum two elements ago
                pick += prev2;
            }
            // Maximum sum if we don't pick current element
            let nonPick = 0 + prev;

            // Maximum at the current element
            let cur_i = Math.max(pick, nonPick);

            prev2 = prev;
            prev = cur_i;
        }
        // Return the maximum sum
        return prev;
    }

    // Function to find the maximum money robber can rob
    houseRobber(money) {
        let n = money.length;
        if (n === 0)
            return 0;
        if (n === 1)
            return money[0];

        // Exclude last element
        let arr1 = money.slice(0, n - 1);  
        
        // Exclude first element
        let arr2 = money.slice(1);         
        
        let ans1 = this.func(arr1);
        let ans2 = this.func(arr2);

        // Return the maximum of ans1 and ans2
        return Math.max(ans1, ans2);
    }
}

let arr = [1, 5, 1, 2, 6];

//Create an instance of Solution class
let sol = new Solution();

console.log(sol.houseRobber(arr));

Complexity Analysis:

Time Complexity: O(N)+O(N), where N is the given size of array. As each element of the array is processed exactly once in a single pass and the array is being called twice.

Space Complexity:O(N)+O(N), as two additional arrays are used to sotre the elements.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Modification to the article on maximum sum of non-adjacent elements:

Approach to solving the problem:

Steps to form recursive solution:

Complexity Analysis:

Steps to convert Recursive code to memoization solution:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code