Letter Combinations of a Phone Number
Recursion
Hard
Hard
- A practical application of this programming problem lies in the creation of telephone dial-in systems or mobile texting in old feature phones, where a combination of number presses resulted in different letters
- The predictive text (T9 word) feature, for instance, used this method to help users type faster
- The logic behind typing on old mobile phones is similar to the problem mentioned - every number corresponds to a different set of letters and a combination results in different words
- Nowadays, even though smartphones with full QWERTY keyboards are dominant, this concept is very crucial for accessibility programs for visually impaired or specially-abled users
Given a string consisting of digits from 2 to 9 (inclusive). Return all possible letter combinations that the number can represent.
Mapping of digits to letters is given in first example.
Examples:
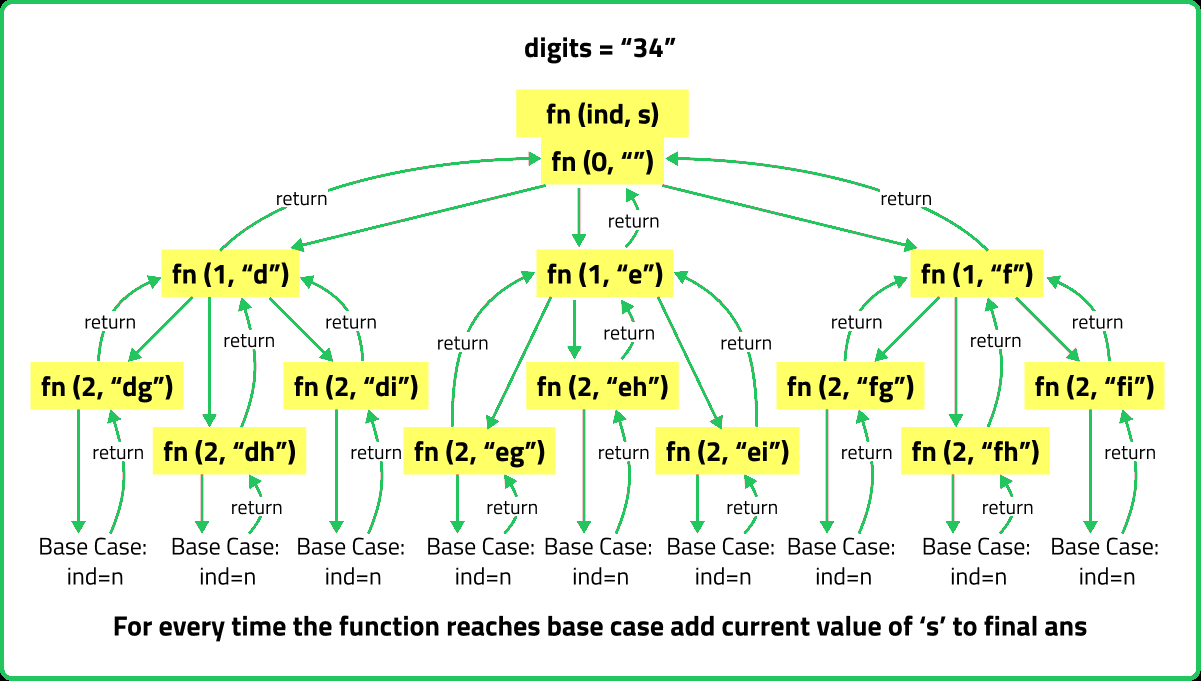
Input : digits = "34"
Output : [ "dg", "dh", "di", "eg", "eh", "ei", "fg", "fh", "fi" ]
Explanation : The 3 is mapped with "def" and 4 is mapped with "ghi".
So all possible combination by replacing the digits with characters are shown in output.

Input : digits = "3"
Output : [ "d", "e", "f" ]
Explanation : The 3 is mapped with "def".
Input : digits = "8"
Constraints
- 0 <= digits.length <= 4
- digts[i] contains digitd from [2,9].
Hints
- Use recursion to explore all combinations. For each digit, iterate over its mapped letters. Append each letter to the current combination and proceed to the next digit.
- Start with an empty combination in a queue. For each digit, extend all existing combinations in the queue by appending each possible letter. Continue until all digits have been processed.
Company Tags
Stripe
HCL Technologies
IBM
Goldman Sachs
Boston Consulting Group
Broadcom
Dropbox
Epic Systems
Cerner
Flipkart
Ernst & Young
Epic Games
Chewy
HashiCorp
Qualcomm
Square
Morgan Stanley
MongoDB
Micron Technology
OYO Rooms
Intel
Mastercard
Shopify
Nutanix
Seagate Technology
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe