Matrix Median

Binary Search 2D Arrays Hard

In the field of image processing and computer graphics, a similar problem is frequently encountered
Pixels of an image are typically represented as a 2D matrix
Operations like median filtering, which involves finding the median of a submatrix or neighborhood of pixels, are applied to remove 'salt and pepper' noise from images while keeping the edges intact
Hence, understanding how to efficiently compute the median of a 2D matrix is crucial in these areas

Given a 2D array matrix that is row-wise sorted. The task is to find the median of the given matrix.

Examples:

Input: matrix=[ [1, 4, 9], [2, 5, 6], [3, 8, 7] ]

Output: 5

Explanation: If we find the linear sorted array, the array becomes 1 2 3 4 5 6 7 8 9. So, median = 5

Input: matrix=[ [1, 3, 8], [2, 3, 4], [1, 2, 5] ]

Output: 3

Explanation:If we find the linear sorted array, the array becomes 1 1 2 2 3 3 4 5 7 8. So, median = 3

Input: matrix=[ [1, 4, 15], [2, 5, 6], [3, 8, 11] ]

Constraints

N==matrix.size
M==matrix[0].size
1 <= N, M <= 10⁵
1 <= N*M <= 10⁶
1 <= matrix[i] <= 10⁹
N*M is odd

Hints

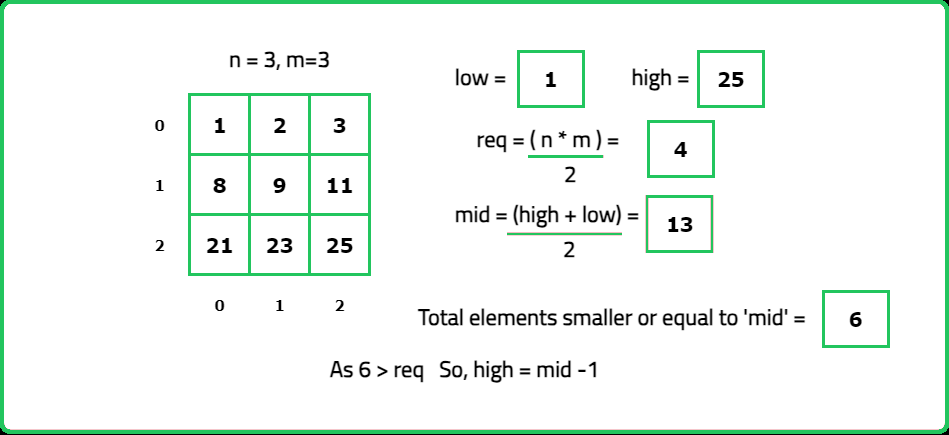
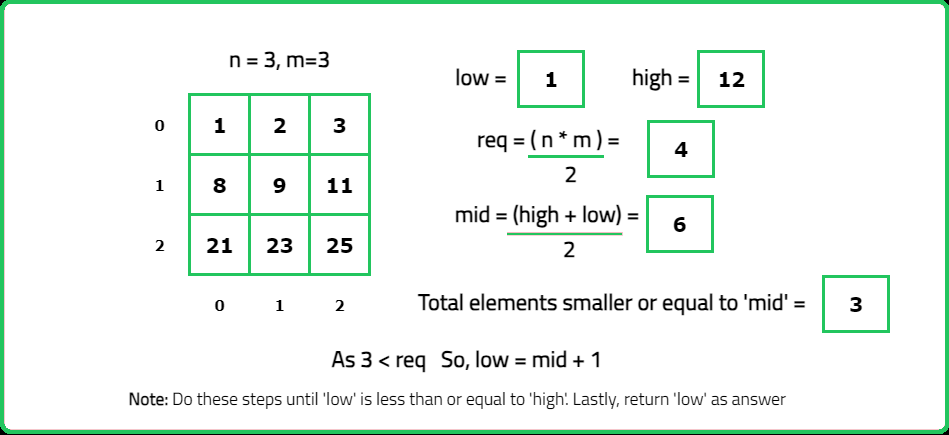
Adjust the binary search range based on whether the count is greater or less than the desired position of the median.
"Since each row is sorted, count the number of elements ≤mid efficiently for each row using binary search (O(logm) per row). Sum the counts for all rows to get the total number of elements ≤ mid."

Company Tags

Optum Wayfair Riot Games Mastercard Electronic Arts Ernst & Young Docker McKinsey & Company Zynga Micron Technology IBM Zoho Roche Western Digital Etsy eBay NVIDIA Philips Healthcare Twilio PayPal Boston Consulting Group Dropbox Square Rakuten Bloomberg Google Microsoft Amazon Meta Apple Netflix Adobe

Intuition:

The extremely naive approach is to use a linear array or list to store the elements of the given matrix and sort them in increasing manner. The middle element will be the median of matrix.

Approach:

Traverse the rows of the matrix using a for loop.
Next, traverse each column of the current row using a nested for loop.
Inside the loops, store each element of the current cell to a linear array or list.
Finally, return the middle element of that linear array.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find the median of the matrix.
    int findMedian(vector<vector<int>>& matrix) {
        vector<int> lst;
        int n = matrix.size();
        int m = matrix[0].size(); 
        
        /* Traverse the matrix and 
        copy the elements to list*/
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                lst.push_back(matrix[i][j]);
            }
        }
        
        // Sort the list
        sort(lst.begin(), lst.end());
        
        // Return the median element
        return lst[(n * m) / 2];
    }
};

int main() {
    vector<vector<int>> matrix = {
        {1, 2, 3, 4, 5},
        {8, 9, 11, 12, 13},
        {21, 23, 25, 27, 29}
    };
    
    //Create an instance of Solution class
    Solution sol;
    
    int ans = sol.findMedian(matrix);
    
    //Print the answer
    cout << "The median element is: " << ans << endl;
    
    return 0;
}
import java.util.*;

class Solution {
    // Function to find the median of the matrix.
    public int findMedian(int[][] matrix) {
        List<Integer> lst = new ArrayList<>();
        int n = matrix.length;
        int m = matrix[0].length;

        /* Traverse the matrix and 
           copy the elements to list */
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                lst.add(matrix[i][j]);
            }
        }

        // Sort the list
        Collections.sort(lst);

        // Return the median element
        return lst.get((n * m) / 2);
    }

    public static void main(String[] args) {
        int[][] matrix = {
            {1, 2, 3, 4, 5},
            {8, 9, 11, 12, 13},
            {21, 23, 25, 27, 29}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        int ans = sol.findMedian(matrix);

        // Print the answer
        System.out.println("The median element is: " + ans);
    }
}
class Solution:
    # Function to find the median of the matrix.
    def findMedian(self, matrix):
        lst = []
        n = len(matrix)
        m = len(matrix[0])
        
        """ Traverse the matrix and 
            copy the elements to list """
        for i in range(n):
            for j in range(m):
                lst.append(matrix[i][j])
        
        # Sort the list
        lst.sort()
        
        # Return the median element
        return lst[(n * m) // 2]

if __name__ == "__main__":
    matrix = [
        [1, 2, 3, 4, 5],
        [8, 9, 11, 12, 13],
        [21, 23, 25, 27, 29]
    ]
    
    # Create an instance of Solution class
    sol = Solution()
    
    ans = sol.findMedian(matrix)
    
    # Print the answer
    print("The median element is:", ans)
class Solution {
    // Function to find the median of the matrix.
    findMedian(matrix) {
        let lst = [];
        let n = matrix.length;
        let m = matrix[0].length;
        
        /* Traverse the matrix and 
        copy the elements to list */
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < m; j++) {
                lst.push(matrix[i][j]);
            }
        }
        
        // Sort the list
        lst.sort((a, b) => a - b);
        
        // Return the median element
        return lst[Math.floor((n * m) / 2)];
    }
}

let matrix = [
    [1, 2, 3, 4, 5],
    [8, 9, 11, 12, 13],
    [21, 23, 25, 27, 29]
];

// Create an instance of Solution class
let sol = new Solution();

let ans = sol.findMedian(matrix);

// Print the answer
console.log("The median element is:", ans);

Complexity Analysis:

Time Complexity: O(M*N) + O(M*N(log(M*N))), where N is the number of rows in the matrix, M is the number of columns in each row. At first, the matrix is traversed to copy the elements, which takes O(MxN) time complexity. Then, the linear array of size (MxN) is sorted, which takes O(MxN log(MxN)) time complexity.

Space Complexity: O(M*N), As a temporary list is used to store the elements of the matrix.

Intuition:

Here, the idea is to use the binary search algorithm to find the median of the matrix. To apply binary search, the search range should be sorted. In this case, the search range is [min, max], where min is the minimum element of the matrix and max is the maximum element of the matrix.

How to check if the current element(mid) is the median:

If current element is the median, the number of elements smaller or equal to current element will surely be greater than (M*N) // 2 (integer division).

How to check how many numbers are smaller or equal to an element ‘mid’:

One way is to traverse the entire matrix and count the numbers, but in that case, the time complexity would be high. Therefore, other approaches need to be considered. It is noted that the matrix is sorted row-wise, so the concept of upper bound can be applied.
For every particular row, the upper bound of the current element 'mid' will be found. The returned index will indicate the number of smaller or equal elements in that row. This process will be repeated for each row, and the results will be aggregated to obtain the total number for the entire matrix.

Approach:

Working of findMedian(matrix):

Calculate the minimum and maximum values of the matrix. Since the given matrix is sorted row-wise, the minimum element will be found in the first column, and the maximum element will be found in the last column.
The pointers low and high are placed as follows: Initially, the pointer low points to the minimum element of the matrix, and the pointer high points to the maximum element of the matrix.
Initialize a while loop which will run till low is less than or equal to high. Calculate mid as (low+high) // 2 ( ‘//’ refers to integer division).
The calculateSmallEqual() function is used to obtain the number of elements less than or equal to mid. Within the function, the upper bound formula mentioned above is applied to each row to calculate the total number of elements less than or equal to mid. The total number is then returned from the calculateSmallEqual() function.
If smallEqual is less than or equal to (M*N) // 2, it can be concluded that the median must be a larger number. Therefore, the left half (smaller values) is eliminated by setting low = mid + 1.
If smallEqual is greater than (M*N) // 2, it can be concluded that the element mid might be the median. However, to determine the actual median, we need to move towards smaller numbers. Therefore, in this case, the right half (larger values) is eliminated by setting high = mid - 1.

Working of upperBound(arr, x,m):

This helper functions finds out the upper bound of x in the the array.
Start with low = 0 and high = m - 1, where m is the size of the array arr. Initialize ans to m, which serves as the default answer assuming all elements might be less than or equal to x.
Use a while loop to perform binary search until low exceeds high.Calculate the 'mid' index as (low + high) / 2.
If arr[mid] is greater than x. This means it's a potential candidate for being the upper bound (first element greater than x). Update ans to mid, indicating that we found a potential upper bound. Then adjust high to (mid - 1) to search for a potentially smaller upper bound on the left side of mid. Otherwise, move low to (mid + 1) to search for the upper bound on the right side of mid
Once the while loop terminates, return the 'ans' variable.

Working of countSmallEqual(matrix, n, m, x):

Start with cnt = 0, which will store the count of elements in the matrix that are less than or equal to x.
Iterate through each row of the matrix and call upperBound(),
The upperBound function returns the index of the first element in the current row that is greater than x. Add the returned index to cnt. This addition effectively counts all elements in the current row matrix[i] that are less than or equal to x.
After iterating through all rows and accumulating counts, return 'cnt', which represents the total number of elements in the entire matrix matrix that are less than or equal to x.

#include<bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Function to find the upper bound of an element
    int upperBound(vector<int>& arr, int x, int m) {
        int low = 0, high = m - 1;
        int ans = m;
        
        //Apply binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            
            /* If arr[mid] > x, it 
            can be a possible answer*/
            if (arr[mid] > x) {
                ans = mid;
                //Look for smaller index on the left
                high = mid - 1;
            }
            else {
                low = mid + 1; 
            }
        }
        //Return the answer
        return ans;
    }
    /*Function to find the count of 
    element smaller than x or equal to x*/
    int countSmallEqual(vector<vector<int>>& matrix, int n, int m, int x) {
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            cnt += upperBound(matrix[i], x, m);
        }
        //Returnt the count
        return cnt;
    }
public:
    //Function to find the median in a matrix
    int findMedian(vector<vector<int>>& matrix) {
        int n = matrix.size();
        int m = matrix[0].size();
        
        //Intialize low and high
        int low = INT_MAX, high = INT_MIN;

        //Point low and high to right elements
        for (int i = 0; i < n; i++) {
            low = min(low, matrix[i][0]);
            high = max(high, matrix[i][m - 1]);
        }

        int req = (n * m) / 2;
        
        //Perform binary search
        while (low <= high) {
            int mid = low + (high - low) / 2;
            
            /*Store the count of elements
            lesser than or equal to mid*/
            int smallEqual = countSmallEqual(matrix, n, m, mid);
            if (smallEqual <= req) low = mid + 1;
            else high = mid - 1;
        }
        //Return low as answer
        return low;
    }
};
int main() {
    vector<vector<int>> matrix = {{1, 2, 3, 4, 5},
                                  {8, 9, 11, 12, 13},
                                  {21, 23, 25, 27, 29}};
    
    //Create an instance of Solution class
    Solution sol;
    
    int ans = sol.findMedian(matrix);
    
    //Print the output
    cout << "The median element is: " << ans << endl;
    return 0;
}
import java.util.*;

class Solution {
    // Function to find the upper bound of an element
    private int upperBound(int[] arr, int x, int m) {
        int low = 0, high = m - 1;
        int ans = m;
        
        // Apply binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            
            // If arr[mid] > x, it can be a possible answer
            if (arr[mid] > x) {
                ans = mid;
                // Look for smaller index on the left
                high = mid - 1;
            } else {
                low = mid + 1; 
            }
        }
        // Return the answer
        return ans;
    }
    
    // Function to find the count of elements smaller than or equal to x
    private int countSmallEqual(int[][] matrix, int n, int m, int x) {
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            cnt += upperBound(matrix[i], x, m);
        }
        // Return the count
        return cnt;
    }
    
    // Function to find the median in a matrix
    public int findMedian(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        
        // Initialize low and high
        int low = Integer.MAX_VALUE, high = Integer.MIN_VALUE;
        
        // Point low and high to right elements
        for (int i = 0; i < n; i++) {
            low = Math.min(low, matrix[i][0]);
            high = Math.max(high, matrix[i][m - 1]);
        }
        
        int req = (n * m) / 2;
        
        // Perform binary search
        while (low <= high) {
            int mid = low + (high - low) / 2;
            
            /* Store the count of elements
            lesser than or equal to mid */
            int smallEqual = countSmallEqual(matrix, n, m, mid);
            if (smallEqual <= req) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        // Return low as answer
        return low;
    }
    
    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3, 4, 5},
                          {8, 9, 11, 12, 13},
                          {21, 23, 25, 27, 29}};
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        int ans = sol.findMedian(matrix);
        
        // Print the output
        System.out.println("The median element is: " + ans);
    }
}
class Solution:
    
    # Function to find the upper bound of an element
    def upperBound(self, arr, x, m):
        low, high = 0, m - 1
        ans = m
        
        # Apply binary search
        while low <= high:
            mid = (low + high) // 2
            
            # If arr[mid] > x, it can be a possible answer
            if arr[mid] > x:
                ans = mid
                # Look for smaller index on the left
                high = mid - 1
            else:
                low = mid + 1
                
        # Return the answer
        return ans
    
    # Function to find the count of elements smaller than or equal to x
    def countSmallEqual(self, matrix, n, m, x):
        cnt = 0
        for i in range(n):
            cnt += self.upperBound(matrix[i], x, m)
        
        # Return the count
        return cnt
    
    # Function to find the median in a matrix
    def findMedian(self, matrix):
        n = len(matrix)
        m = len(matrix[0])
        
        # Initialize low and high
        low = float('inf')
        high = float('-inf')
        
        # Point low and high to right elements
        for i in range(n):
            low = min(low, matrix[i][0])
            high = max(high, matrix[i][m - 1])
        
        req = (n * m) // 2
        
        # Perform binary search
        while low <= high:
            mid = low + (high - low) // 2
            
            """ Store the count of elements 
            lesser than or equal to mid"""
            smallEqual = self.countSmallEqual(matrix, n, m, mid)
            if smallEqual <= req:
                low = mid + 1
            else:
                high = mid - 1
        
        # Return low as answer
        return low
    
if __name__ == "__main__":
    matrix = [[1, 2, 3, 4, 5],
              [8, 9, 11, 12, 13],
              [21, 23, 25, 27, 29]]
    
    # Create an instance of Solution class
    sol = Solution()
    
    ans = sol.findMedian(matrix)
    
    # Print the output
    print(f"The median element is: {ans}")
class Solution {
    // Function to find the upper bound of an element
    upperBound(arr, x, m) {
        let low = 0, high = m - 1;
        let ans = m;
        
        // Apply binary search
        while (low <= high) {
            let mid = Math.floor((low + high) / 2);
            
            // If arr[mid] > x, it can be a possible answer
            if (arr[mid] > x) {
                ans = mid;
                // Look for smaller index on the left
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        // Return the answer
        return ans;
    }
    
    // Function to find the count of elements smaller than or equal to x
    countSmallEqual(matrix, n, m, x) {
        let cnt = 0;
        for (let i = 0; i < n; i++) {
            cnt += this.upperBound(matrix[i], x, m);
        }
        // Return the count
        return cnt;
    }
    
    // Function to find the median in a matrix
    findMedian(matrix) {
        let n = matrix.length;
        let m = matrix[0].length;
        
        // Initialize low and high
        let low = Number.MAX_SAFE_INTEGER;
        let high = Number.MIN_SAFE_INTEGER;
        
        // Point low and high to right elements
        for (let i = 0; i < n; i++) {
            low = Math.min(low, matrix[i][0]);
            high = Math.max(high, matrix[i][m - 1]);
        }
        
        let req = Math.floor((n * m) / 2);
        
        // Perform binary search
        while (low <= high) {
            let mid = low + Math.floor((high - low) / 2);
            
            /* Store the count of elements
            lesser than or equal to mid*/
            let smallEqual = this.countSmallEqual(matrix, n, m, mid);
            if (smallEqual <= req) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        // Return low as answer
        return low;
    }
}

const matrix = [[1, 2, 3, 4, 5],
                [8, 9, 11, 12, 13],
                [21, 23, 25, 27, 29]];

// Create an instance of Solution class
const sol = new Solution();

console.log(sol.findMedian(matrix));

Complexity Analysis:

Time Complexity: O(log(max)) * O(M(logN)), where N is the number of rows in the matrix, M is the number of columns in each row. Our search space ranges from [min, max], where min is the minimum and max is the maximum element of the matrix. Binary search is applied within this search space, which operates with a time complexity of O(log(max)). Then, the countSmallEqual() function is called for each 'mid', which has a time complexity of O(M*log(N)).

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Code

Problem List

Matrix Median

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code