Cherry pickup II

Why Greedy Approach will not work:

As we have to return the maximum cherries collected, the first approach that comes to our mind is to take a greedy approach and always form a path by locally choosing the option that gives us more cherries. But there is no ‘uniformity’ in the values of the matrix.Therefore, it can happen that whenever we make a local choice that gives us a better path, we actually take a path that, in later stages, yields fewer cherries.

As a greedy solution doesn’t work, our next choice will be to try out all the possible paths. To generate all possible paths we will use recursion.

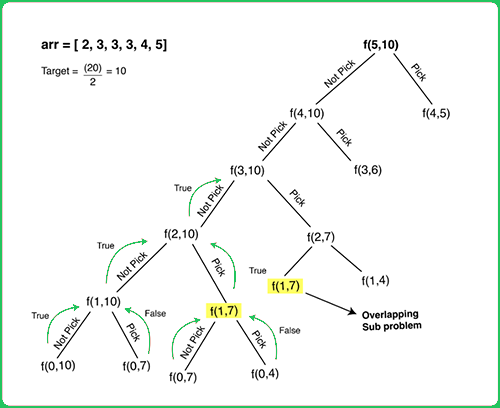
In this question, there are fixed starting points but variable ending points, but as per the movements of robots, we know that they will end in the last row. They have to move together at a time to the next row because if we seperately find the maximum cherries picked up by each robot, it can happen that the same cell cherries gets counted twice for each of the robots.

Steps to form the recursive solution:

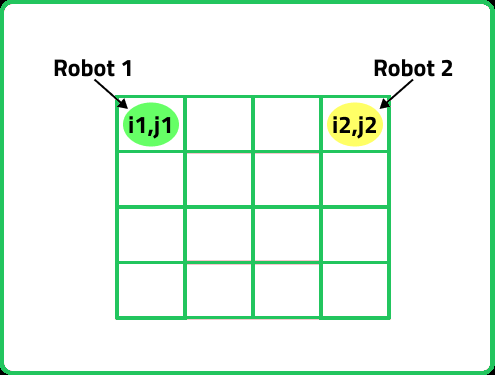
Express the problem in terms of indexes: This question is slightly different from all the previous questions, here we are given two starting points from where the two robots can move. We are given an ‘N*M’ matrix. Therefore, four parameters i1,j1,i2, and j2 needs to be defined, to describe the positions of both of the robots. Each pair(i, j) wil describe the present cell of each of the robots.

If we observe, initially the two robots are at the first row, and they always move to the row below them every time, so they will always be in the same row. Therefore two different variables i1 and i2, to describe their positions are redundant. We can just use single parameter i, which tells us in which row of the grid both of them are.

Hence the function can be modified to take 3 parameters only. 'i', 'j1' and 'j2'. f(i, j1, j2) will give the maximum number of cherries collected by 1st robot from cell[i, j1] till last row and 2nd robot from cell[i, j2] till last row combined.

Try out all possible choices at a given index: At every cell, there are 3 choices for each robot, to the bottom cell, to the bottom-right cell or to the bottom-left cell. Now, we need to understand that both of the robots needs to move together. Both of them can individually take three moves but say one of them moves to bottom-left, then the other one can have three different choices for each move taken by the first robot.

Hence there are total of 9 different options at every f(i, j1, j2) to move both the robots together. Now we can manually write these 9 options or we can observe a pattern in them, first ont of the robots moves to one side and the other one takes tries all three choices, then again the first robot moves, then the second one, and so on. This pattern can be easily captured by using two nested loops that change the column numbers(j1 and j2).

Note:If (j1===j2), as discussed in the base case, only consider cherries collected by one of them otherwise consider cherries collected by both of them.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j1, j2){
    //Base case
    for(di = -1; di <= 1; di++){
        for(dj = -1; dj <=1; dj++){
            ans = 0;
            if(j1 == j2){
                ans = mat[i][j1] + f(i + 1, j1 + di, j2 + dj)
            else
                ans = mat[i][j1] + mat[i][j2] + f(i + 1, j1 + di, j2 + dj)
            }
        }
    }
}

Take the maximum of all choices: As we need to find the maximum cherries picked, return the maximum of the choices.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j1, j2){
    //Base case
    maxi = INT_MIN
    for(di = -1; di <= 1; di++){
        for(dj = -1; dj <=1; dj++){
            ans = 0;
            if(j1 == j2)
                ans = mat[i][j1] + f(i + 1, j1 + di, j2 + dj)
            else
                ans = mat[i][j1] + mat[i][j2] + f(i + 1, j1 + di, j2 + dj)
            maxi = max(maxi, ans)
        }
    }
    return maxi
}

Base cases: When i == N-1, it means we are at the last row, so we need to return from here. Now it can happen that in the last row, both the robots are at the same cell, in this condition return cherries collected by one of them only, mat[i][j1], otherwise return sum of cherries collected by both, mat[i][j1] + mat[i][j1][j2].

At every cell, there are 3 choices individually, to the bottom cell, to the bottom-right cell or to the bottom-left cell. As the robots are moving to the bottom row, at max they will reach the last row, from where they return, so they will never go out of the bounding index.

To move to the bottom-right cell or to the bottom-left cell, it can happen that robots may go out of bound. So we need to handle that case, return -1e9, whenever robots go out of bound, in this way this path will not be selected by the calling function as we have to return the maximum cherries.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j1, j2){
    if(j1 < 0 || j1>= m || j2 < 0 || j2 >= m)   return -1e9
    if(i == n-1) {
        if(j1 == j2)
            return mat[i][j1]
        else
            return mat[i][j1] + mat[i][j2]
    }  
}

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to find the maximum cherries
    that can be collected recursively*/
    int func(int i, int j1, int j2, int n, int m, vector<vector<int>> &matrix) {
        // Base cases
        if (j1 < 0 || j1 >= m || j2 < 0 || j2 >= m)
        return -1e9; 

        if (i == n - 1) {
            if (j1 == j2)
                return matrix[i][j1];
            else
                return matrix[i][j1] + matrix[i][j2];
        }

        int maxi = INT_MIN;
    
        // Try all possible moves for both positions (j1, j2)
        for (int di = -1; di <= 1; di++) {
            for (int dj = -1; dj <= 1; dj++) {
                int ans;
            
                if (j1 == j2)
                    ans = matrix[i][j1] + func(i + 1, j1 + di, j2 + dj, n, m, matrix);
                else
                    ans = matrix[i][j1] + matrix[i][j2] + func(i + 1, j1 + di, j2 + dj, n, m, matrix);
            
                // Update the maximum result
                maxi = max(maxi, ans);
            }
        }
    
        //Return the maximum cherries collected
        return maxi;
    }
public:
    // Function to find maximum cherries that can be collected
    int cherryPickup(vector<vector<int>> &matrix) {
        int n = matrix.size();
        int m = matrix[0].size();

        //Return the maximum cherries collected
        return func(0, 0, m - 1, n, m, matrix);
    }
};

int main() {
    vector<vector<int>> matrix{
        {2, 3, 1, 2},
        {3, 4, 2, 2},
        {5, 6, 3, 5},
    };
    
    //Create an instance of Solution class
    Solution sol;

    // Call the function and print the result
    cout << sol.cherryPickup(matrix);

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the maximum cherries
    that can be collected recursively*/
    private int func(int i, int j1, int j2, int n, int m, int[][] matrix) {
        // Base cases
        if (j1 < 0 || j1 >= m || j2 < 0 || j2 >= m)
            return (int)(-1e9);

        if (i == n - 1) {
            if (j1 == j2)
                return matrix[i][j1];
            else
                return matrix[i][j1] + matrix[i][j2];
        }

        int maxi = Integer.MIN_VALUE;

        // Try all possible moves for both positions (j1, j2)
        for (int di = -1; di <= 1; di++) {
            for (int dj = -1; dj <= 1; dj++) {
                int ans;

                if (j1 == j2)
                    ans = matrix[i][j1] + func(i + 1, j1 + di, j2 + dj, n, m, matrix);
                else
                    ans = matrix[i][j1] + matrix[i][j2] + func(i + 1, j1 + di, j2 + dj, n, m, matrix);

                // Update the maximum result
                maxi = Math.max(maxi, ans);
            }
        }

        // Return the maximum cherries collected
        return maxi;
    }
    // Function to find maximum cherries that can be collected
    public int cherryPickup(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;

        // Return the maximum cherries collected
        return func(0, 0, m - 1, n, m, matrix);
    }

    public static void main(String[] args) {
        int[][] matrix = {
                {2, 3, 1, 2},
                {3, 4, 2, 2},
                {5, 6, 3, 5}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the function and print the result
        System.out.println(sol.cherryPickup(matrix));
    }
}
class Solution:
    """ Function to find the maximum cherries
    that can be collected recursively"""
    def func(self, i, j1, j2, n, m, matrix):
        # Base cases
        if j1 < 0 or j1 >= m or j2 < 0 or j2 >= m:
            return -1e9

        if i == n - 1:
            if j1 == j2:
                return matrix[i][j1]
            else:
                return matrix[i][j1] + matrix[i][j2]

        maxi = -float('inf')

        # Try all possible moves for both positions (j1, j2)
        for di in range(-1, 2):
            for dj in range(-1, 2):
                ans = 0

                if j1 == j2:
                    ans = matrix[i][j1] + self.func(i + 1, j1 + di, j2 + dj, n, m, matrix)
                else:
                    ans = matrix[i][j1] + matrix[i][j2] + self.func(i + 1, j1 + di, j2 + dj, n, m, matrix)

                # Update the maximum result
                maxi = max(maxi, ans)

        # Return the maximum cherries collected
        return maxi
    # Function to find maximum cherries that can be collected
    def cherryPickup(self, matrix):
        n = len(matrix)
        m = len(matrix[0])

        # Return the maximum cherries collected
        return self.func(0, 0, m - 1, n, m, matrix)

if __name__ == "__main__":
    matrix = [
        [2, 3, 1, 2],
        [3, 4, 2, 2],
        [5, 6, 3, 5]
    ]

    # Create an instance of Solution class
    sol = Solution()

    # Call the function and print the result
    print(sol.cherryPickup(matrix))
class Solution {
    /* Function to find the maximum cherries
    that can be collected recursively*/
    func(i, j1, j2, n, m, matrix) {
        // Base cases
        if (j1 < 0 || j1 >= m || j2 < 0 || j2 >= m)
            return -1e9;

        if (i === n - 1) {
            if (j1 === j2)
                return matrix[i][j1];
            else
                return matrix[i][j1] + matrix[i][j2];
        }

        let maxi = -Infinity;

        // Try all possible moves for both positions (j1, j2)
        for (let di = -1; di <= 1; di++) {
            for (let dj = -1; dj <= 1; dj++) {
                let ans;

                if (j1 === j2)
                    ans = matrix[i][j1] + this.func(i + 1, j1 + di, j2 + dj, n, m, matrix);
                else
                    ans = matrix[i][j1] + matrix[i][j2] + this.func(i + 1, j1 + di, j2 + dj, n, m, matrix);

                // Update the maximum result
                maxi = Math.max(maxi, ans);
            }
        }

        // Return the maximum cherries collected
        return maxi;
    }
    // Function to find maximum cherries that can be collected
    cherryPickup(matrix) {
        const n = matrix.length;
        const m = matrix[0].length;

        // Return the maximum cherries collected
        return this.func(0, 0, m - 1, n, m, matrix);
    }
}

// Test case
let matrix = [
    [2, 3, 1, 2],
    [3, 4, 2, 2],
    [5, 6, 3, 5]
];

// Create an instance of Solution class
let sol = new Solution();

// Call the function and print the result
console.log(sol.cherryPickup(matrix));

Time Complexity: O(3^(N)*3^(N)), where N is the number of row. As, for each cell, each of the robots has 3 options and there are N rows to be considered.

Space Complexity:O(N), at maximum the depth of the recursive stack can go upto N.

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][m][m]: As there are three changing parameters(i, j1 and j2) in the recursive solution, and the maximum value they can attain is (n-1) for 'i' as it detones the row and (m-1) for both 'j1' and 'j2' as it denotes the column. So we will require a dp matrix of n*m*m.

The dp array stores the calculations of subproblems, dp[i][j1][j2] represents the maximum number of cherries collected by 1st robot from cell[i, j1] till last row and 2nd robot from cell[i, j2] till last row combined. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to find the maximum cherries
    that can be collected using memoization*/
    int func(int i, int j1, int j2, int n, int m, vector<vector<int>> &matrix, vector<vector<vector<int>>> &dp) {
        // Base cases
        if (j1 < 0 || j1 >= m || j2 < 0 || j2 >= m)
        return -1e9; 

        if (i == n - 1) {
            if (j1 == j2)
                return matrix[i][j1];
            else
                return matrix[i][j1] + matrix[i][j2];
        }
        
        /* If the result for this state 
        is already computed, return it*/
        if (dp[i][j1][j2] != -1)
            return dp[i][j1][j2];

        int maxi = INT_MIN;
    
        // Try all possible moves for both positions (j1, j2)
        for (int di = -1; di <= 1; di++) {
            for (int dj = -1; dj <= 1; dj++) {
                int ans;
            
                if (j1 == j2)
                    ans = matrix[i][j1] + func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp);
                else
                    ans = matrix[i][j1] + matrix[i][j2] + func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp);
            
                // Update the maximum result
                maxi = max(maxi, ans);
            }
        }
    
        // Store the maximum result for this state in dp
        return dp[i][j1][j2] = maxi;
    }
public:
    // Function to find maximum cherries that can be collected
    int cherryPickup(vector<vector<int>> &matrix) {
        int n = matrix.size();
        int m = matrix[0].size();
        
        // Initialize a 3D DP array to store computed results
        vector<vector<vector<int>>> dp(n, vector<vector<int>>(m, vector<int>(m, -1)));

        //Return the maximum cherries collected
        return func(0, 0, m - 1, n, m, matrix, dp);
    }
};

int main() {
    vector<vector<int>> matrix{
        {2, 3, 1, 2},
        {3, 4, 2, 2},
        {5, 6, 3, 5},
    };
    
    //Create an instance of Solution class
    Solution sol;

    // Call the function and print the result
    cout << sol.cherryPickup(matrix);

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the maximum cherries
    that can be collected using memoization*/
    private int func(int i, int j1, int j2, int n, int m, int[][] matrix, int[][][] dp) {
        // Base cases
        if (j1 < 0 || j1 >= m || j2 < 0 || j2 >= m)
            return (int)(-1e9);

        if (i == n - 1) {
            if (j1 == j2)
                return matrix[i][j1];
            else
                return matrix[i][j1] + matrix[i][j2];
        }
        
        /* If the result for this state 
        is already computed, return it*/
        if (dp[i][j1][j2] != -1)
            return dp[i][j1][j2];

        int maxi = Integer.MIN_VALUE;

        // Try all possible moves for both positions (j1, j2)
        for (int di = -1; di <= 1; di++) {
            for (int dj = -1; dj <= 1; dj++) {
                int ans;

                if (j1 == j2)
                    ans = matrix[i][j1] + func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp);
                else
                    ans = matrix[i][j1] + matrix[i][j2] + func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp);

                // Update the maximum result
                maxi = Math.max(maxi, ans);
            }
        }

        // Store the result in the dp array and return it
        return dp[i][j1][j2] = maxi;
    }
    // Function to find maximum cherries that can be collected
    public int cherryPickup(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        
        // Declare a 3D array to store computed results
        int dp[][][] = new int[n][m][m];

        // Initialize the dp array with -1
        for (int row1[][] : dp) {
            for (int row2[] : row1) {
                Arrays.fill(row2, -1);
            }
        }
   
        // Return the maximum cherries collected
        return func(0, 0, m - 1, n, m, matrix, dp);
    }

    public static void main(String[] args) {
        int[][] matrix = {
                {2, 3, 1, 2},
                {3, 4, 2, 2},
                {5, 6, 3, 5}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the function and print the result
        System.out.println(sol.cherryPickup(matrix));
    }
}
class Solution:
    """ Function to find the maximum cherries
    that can be collected using memoization"""
    def func(self, i, j1, j2, n, m, matrix, dp):
        # Base cases
        if j1 < 0 or j1 >= m or j2 < 0 or j2 >= m:
            return int(-1e9)

        if i == n - 1:
            if j1 == j2:
                return matrix[i][j1]
            else:
                return matrix[i][j1] + matrix[i][j2]
        
        """ If the result for these indices has
        already been computed, return it"""
        if dp[i][j1][j2] != -1:
            return dp[i][j1][j2]

        maxi = int(-1e9)

        # Try all possible moves for both positions (j1, j2)
        for di in range(-1, 2):
            for dj in range(-1, 2):
                ans = 0

                if j1 == j2:
                    ans = matrix[i][j1] + self.func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp)
                else:
                    ans = matrix[i][j1] + matrix[i][j2] + self.func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp)

                # Update the maximum result
                maxi = max(maxi, ans)

        """ Store the maximum cherries 
        collected in the memoization table"""
        dp[i][j1][j2] = maxi
        return maxi
        
    # Function to find maximum cherries that can be collected
    def cherryPickup(self, matrix):
        n = len(matrix)
        m = len(matrix[0])
        
        
        # Initialize a memoization table with -1 values
        dp = [[[-1 for j in range(m)] for i in range(m)] for k in range(n)]

        # Return the maximum cherries collected
        return self.func(0, 0, m - 1, n, m, matrix, dp)

if __name__ == "__main__":
    matrix = [
        [2, 3, 1, 2],
        [3, 4, 2, 2],
        [5, 6, 3, 5]
    ]

    # Create an instance of Solution class
    sol = Solution()

    # Call the function and print the result
    print(sol.cherryPickup(matrix))
class Solution {
    /* Function to find the maximum cherries
    that can be collected using memoization*/
    func(i, j1, j2, n, m, matrix, dp) {
        // Base cases
        if (j1 < 0 || j1 >= m || j2 < 0 || j2 >= m)
            return -1e9;

        if (i === n - 1) {
            if (j1 === j2)
                return matrix[i][j1];
            else
                return matrix[i][j1] + matrix[i][j2];
        }
        
        /* If the result for this state 
        is already computed, return it*/
        if (dp[i][j1][j2] != -1)
            return dp[i][j1][j2];
            
        let maxi = -Infinity;

        // Try all possible moves for both positions (j1, j2)
        for (let di = -1; di <= 1; di++) {
            for (let dj = -1; dj <= 1; dj++) {
                let ans;

                if (j1 === j2)
                    ans = matrix[i][j1] + this.func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp);
                else
                    ans = matrix[i][j1] + matrix[i][j2] + this.func(i + 1, j1 + di, j2 + dj, n, m, matrix, dp);

                // Update the maximum result
                maxi = Math.max(maxi, ans);
            }
        }

        // Store the maximum result for this state in dp
        dp[i][j1][j2] = maxi;
        return dp[i][j1][j2];
    }
    // Function to find maximum cherries that can be collected
    cherryPickup(matrix) {
        const n = matrix.length;
        const m = matrix[0].length;
        
        // Initialize a 3D dp array with -1 values
        const dp = new Array(n).fill(null).map(() =>
            new Array(m).fill(null).map(() =>
                new Array(m).fill(-1)
            )
        );

        // Return the maximum cherries collected
        return this.func(0, 0, m - 1, n, m, matrix, dp);
    }
}

// Test case
let matrix = [
    [2, 3, 1, 2],
    [3, 4, 2, 2],
    [5, 6, 3, 5]
];

// Create an instance of Solution class
let sol = new Solution();

// Call the function and print the result
console.log(sol.cherryPickup(matrix));

Complexity Analysis:

Time Complexity: O(N*M*M) * 9. At max, there will be N*M*M calls of recursion to solve a new problem and in every call, two nested loops together run for 9 times.

Space Complexity:O(N) + O(N*M*M). We are using a recursion stack space of O(N), where N is the path length and an external DP Array of size ‘N*M*M’.

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Setting Base Cases in the Array: In the recursive code, our base condition was when we reach the last row, therefore in our dp array, we will also initialize dp[n-1][][], i.e (the last plane of 3D Array) as the base condition. Dp[n-1][j1][j2] means the first robot is at (n-1,j1) and the second robot is at (n-1,j2). As this is the last row, its value will be equal to mat[i][j1], if (j1==j2) and mat[i][j1] + mat[i][j2] otherwise.

Iterative Computation Using Loops: As the last row of the dp is already filled for base condition, now start moving from dp[n-2][][] to dp[0][][]. First set three nested loops to do this traversal.

Inside the three nested loops( say i, j1, j2 as loop variables), use the recursive relations, i.e again set two nested loops to try all the nine options. The outer three loops are just for traversal, and the inner two loops that run for 9 times mainly decide, what should be the value of the cell.

Inside the inner two nested loops, calculate an answer as we had done in the recursive relation, but this time using values from the next plane of the 3D DP Array( dp[i+1][x][y] instead of recursive calls, where x and y will vary according to inner 2 nested loops).

Choosing the maximum: As the question asks for maximum cherries that can be collected so, set dp[i][j1][j2] as the maximum of all the 9 options possible.

Returning the answer: The element dp[0][0][m-1] of the dp array is returned because it holds the optimal solution to the entire problem after the computation has been completed.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
   /* Function to find the maximum cherries 
   that can be collected using tabulation */
   int func(int n, int m, vector<vector<int>> &matrix) {
        // Initialize a 3D DP array to store computed results
        vector<vector<vector<int>>> dp(n, vector<vector<int>>(m, vector<int>(m, 0)));

        // Initialize the DP array for the last row
        for (int j1 = 0; j1 < m; j1++) {
            for (int j2 = 0; j2 < m; j2++) {
                if (j1 == j2)
                    dp[n - 1][j1][j2] = matrix[n - 1][j1];
                else
                    dp[n - 1][j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2];
            }
        }

        /* Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row*/
        for (int i = n - 2; i >= 0; i--) {
            for (int j1 = 0; j1 < m; j1++) {
                for (int j2 = 0; j2 < m; j2++) {
                    int maxi = INT_MIN;

                    // Inner nested loops to try out 9 options 
                    for (int di = -1; di <= 1; di++) {
                        for (int dj = -1; dj <= 1; dj++) {
                            int ans;

                            if (j1 == j2)
                                ans = matrix[i][j1];
                            else
                                ans = matrix[i][j1] + matrix[i][j2];

                            // Check if the move is valid 
                            if ((j1 + di < 0 || j1 + di >= m) || (j2 + dj < 0 || j2 + dj >= m))
                                /* A very large negative value 
                                to represent an invalid move*/
                                ans += -1e9; 
                            else
                                ans += dp[i + 1][j1 + di][j2 + dj]; 
                                
                            // Update the maximum result
                            maxi = max(ans, maxi); 
                        }
                    }
                    /* Store the maximum result for 
                    this state in the DP array*/
                    dp[i][j1][j2] = maxi; 
                }
            }
        }

        /* The maximum cherries that can be collected
        is stored at the top-left corner of the DP array*/
        return dp[0][0][m - 1];
    }
public:
    //Function to find the maximum cherries picked
    int cherryPickup(vector<vector<int>> &matrix){
        int n = matrix.size(); 
        int m = matrix[0].size(); 
        
        //Return the answer
        return func(n, m, matrix);
    }
};
int main() {
    vector<vector<int>> matrix{
        {2, 3, 1, 2},
        {3, 4, 2, 2},
        {5, 6, 3, 5},
    };
    
    //Create an instance of Solution class
    Solution sol;

    // Call the maximumChocolates function and print the result
    cout << sol.cherryPickup(matrix);

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the maximum cherries 
    that can be collected using tabulation*/
    private int func(int n, int m, int[][] matrix) {
        // Initialize a 3D DP array to store computed results
        int[][][] dp = new int[n][m][m];

        // Initialize the DP array for the last row
        for (int j1 = 0; j1 < m; j1++) {
            for (int j2 = 0; j2 < m; j2++) {
                if (j1 == j2)
                    dp[n - 1][j1][j2] = matrix[n - 1][j1];
                else
                    dp[n - 1][j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2];
            }
        }

        /* Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row*/
        for (int i = n - 2; i >= 0; i--) {
            for (int j1 = 0; j1 < m; j1++) {
                for (int j2 = 0; j2 < m; j2++) {
                    int maxi = Integer.MIN_VALUE;

                    // Inner nested loops to try out 9 options 
                    for (int di = -1; di <= 1; di++) {
                        for (int dj = -1; dj <= 1; dj++) {
                            int ans;

                            if (j1 == j2)
                                ans = matrix[i][j1];
                            else
                                ans = matrix[i][j1] + matrix[i][j2];

                            // Check if the move is valid 
                            if ((j1 + di < 0 || j1 + di >= m) || (j2 + dj < 0 || j2 + dj >= m))
                                /* A very large negative value 
                                to represent an invalid move*/
                                ans += -1e9; 
                            else
                                ans += dp[i + 1][j1 + di][j2 + dj]; 
                                
                            // Update the maximum result
                            maxi = Math.max(ans, maxi); 
                        }
                    }
                    /* Store the maximum result for 
                    this state in the DP array*/
                    dp[i][j1][j2] = maxi; 
                }
            }
        }

        /* The maximum cherries that can be collected is
        stored at the top-left corner of the DP array*/
        return dp[0][0][m - 1];
    }

    // Function to find the maximum cherries picked
    public int cherryPickup(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;

        // Return the answer
        return func(n, m, matrix);
    }

    public static void main(String[] args) {
        int[][] matrix = {
            {2, 3, 1, 2},
            {3, 4, 2, 2},
            {5, 6, 3, 5}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call cherryPickup function and print the result
        System.out.println(sol.cherryPickup(matrix));
    }
}
class Solution:
    """ Function to find the maximum cherries 
    that can be collected using tabulation"""
    def func(self, n, m, matrix):
        # Initialize a 3D DP array to store computed results
        dp = [[[0] * m for _ in range(m)] for _ in range(n)]

        # Initialize the DP array for the last row
        for j1 in range(m):
            for j2 in range(m):
                if j1 == j2:
                    dp[n - 1][j1][j2] = matrix[n - 1][j1]
                else:
                    dp[n - 1][j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2]

        """ Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row"""
        for i in range(n - 2, -1, -1):
            for j1 in range(m):
                for j2 in range(m):
                    maxi = float('-inf')

                    # Inner nested loops to try out 9 options 
                    for di in range(-1, 2):
                        for dj in range(-1, 2):
                            ans = 0

                            if j1 == j2:
                                ans = matrix[i][j1]
                            else:
                                ans = matrix[i][j1] + matrix[i][j2]

                            # Check if the move is valid 
                            if (j1 + di < 0 or j1 + di >= m) or (j2 + dj < 0 or j2 + dj >= m):
                                """ A very large negative value 
                                to represent an invalid move"""
                                ans += -1e9
                            else:
                                ans += dp[i + 1][j1 + di][j2 + dj]

                            # Update the maximum result
                            maxi = max(ans, maxi)

                    """ Store the maximum result for
                    this state in the DP array"""
                    dp[i][j1][j2] = maxi

        """ The maximum cherries that can be collected is
        stored at the top-left corner of the DP array"""
        return dp[0][0][m - 1]

    # Function to find the maximum cherries picked
    def cherryPickup(self, matrix):
        n = len(matrix)
        m = len(matrix[0])

        # Return the answer
        return self.func(n, m, matrix)

if __name__ == "__main__":
    matrix = [
        [2, 3, 1, 2],
        [3, 4, 2, 2],
        [5, 6, 3, 5]
    ]

    # Create an instance of Solution class
    sol = Solution()

    # Call cherryPickup function and print the result
    print(sol.cherryPickup(matrix))
class Solution {
    /* Function to find the maximum cherries 
    that can be collected using tabulation*/
    func(n, m, matrix) {
        // Initialize a 3D DP array to store computed results
        let dp = new Array(n);
        for (let i = 0; i < n; i++) {
            dp[i] = new Array(m);
            for (let j = 0; j < m; j++) {
                dp[i][j] = new Array(m).fill(0);
            }
        }

        // Initialize the DP array for the last row
        for (let j1 = 0; j1 < m; j1++) {
            for (let j2 = 0; j2 < m; j2++) {
                if (j1 === j2)
                    dp[n - 1][j1][j2] = matrix[n - 1][j1];
                else
                    dp[n - 1][j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2];
            }
        }

        /* Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row*/
        for (let i = n - 2; i >= 0; i--) {
            for (let j1 = 0; j1 < m; j1++) {
                for (let j2 = 0; j2 < m; j2++) {
                    let maxi = Number.MIN_SAFE_INTEGER;

                    // Iterate through all possible move combinations
                    for (let di = -1; di <= 1; di++) {
                        for (let dj = -1; dj <= 1; dj++) {
                            let ans;

                            if (j1 === j2) {
                                ans = matrix[i][j1];
                            } else {
                                ans = matrix[i][j1] + matrix[i][j2];
                            }

                            // Check if the move is valid
                            if (
                                j1 + di >= 0 && j1 + di < m &&
                                j2 + dj >= 0 && j2 + dj < m
                            ) {
                                ans += dp[i + 1][j1 + di][j2 + dj];
                            } else {
                                // Very large negative value for invalid moves
                                ans += -1e9; 
                            }

                            maxi = Math.max(ans, maxi);
                        }
                    }

                    dp[i][j1][j2] = maxi;
                }
            }
        }

        // The maximum cherries will be stored in dp[0][0][m - 1]
        return dp[0][0][m - 1];
    }
    //Function to find the maximum cherries collected
    cherryPickup(matrix) {
        let n = matrix.length;
        let m = matrix[0].length;

        return this.func(n, m, matrix);
    }
}

const matrix = [
    [2, 3, 1, 2],
    [3, 4, 2, 2],
    [5, 6, 3, 5]
];

// Create an instance of Solution class
const sol = new Solution();

// Call cherryPickup function and print the result
console.log("The maximum cherries that can be collected is", sol.cherryPickup(matrix));

Complexity Analysis:

Time Complexity: O((N*M*M)*9), The outer nested loops run for (N*M*M) times and the inner two nested loops run for 9 times

Space Complexity:O(N*M*M), As an external array of size ‘N*M*M’ is used.

If we observe, we find that to compute dp[i][j1][j2], the value which is needed is from dp[i+1][][] only. Therefore it is not necessary to store a three-dimensional array. Instead, a two-dimensional array can do the same work and we can just update it upon moving from one plane to the other in the 3D Array.

The Steps to space optimize the tabulation approach are as follows:

Initially, take a dummy 2D Array ( say front), initialize this array in the same way it was done in the Tabulation Approach also initialize a 2D Array( say cur), which will be needed in the traversal.

Now set three nested loops to traverse the 3D Array, from the second last plane. Following the same approach as tabulation, find the maximum number of cherries collected at each cell. To calculate it we have all the values in our ‘front’ 2D Array.

Previously, the value of dp[i][j1][j2] was assigned to maxi, now simply assign cur[j1][j2] to maxi. Then whenever the plane of the 3D DP(the first parameter) is going to change, assign the front to cur.

At last, return front[0][m-1] as our answer as it will store the cumulative answer of maximum cherries.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to find the maximum cherries 
    that can be collected usnig space optimization*/
    int func(int n, int m, vector<vector<int>> &matrix){
        /* Declare two 2D vectors 'front' 
        and 'cur' to store computed results*/
        vector<vector<int>> front(m, vector<int>(m, 0));
        vector<vector<int>> cur(m, vector<int>(m, 0));

        // Initialize 'front' for the last row
        for (int j1 = 0; j1 < m; j1++) {
            for (int j2 = 0; j2 < m; j2++) {
                if (j1 == j2)
                    front[j1][j2] = matrix[n - 1][j1];
                else
                    front[j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2];
            }
        }

        /* Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row*/
        for (int i = n - 2; i >= 0; i--) {
            for (int j1 = 0; j1 < m; j1++) {
                for (int j2 = 0; j2 < m; j2++) {
                    int maxi = INT_MIN;

                    // Inner nested loops to try out 9 options 
                    for (int di = -1; di <= 1; di++) {
                        for (int dj = -1; dj <= 1; dj++) {
                            int ans;

                            if (j1 == j2)
                                ans = matrix[i][j1];
                            else
                                ans = matrix[i][j1] + matrix[i][j2];

                            // Check if the move is valid 
                            if ((j1 + di < 0 || j1 + di >= m) || (j2 + dj < 0 || j2 + dj >= m))
                                /* A very large negative value 
                                to represent an invalid move*/
                                ans += -1e9;
                            else
                            ans += front[j1 + di][j2 + dj]; 
                            
                            // Update the maximum result
                            maxi = max(ans, maxi); 
                        }
                    }
                    /* Store the maximum result for 
                    this state in the 'cur' array*/
                    cur[j1][j2] = maxi; 
                }
            }
            /* Update 'front' with the values
            from 'cur' for the next iteration*/
            front = cur; 
        }

        /* The maximum cherries that can be collected
        is stored at the top-left corner of the 'front'*/
        return front[0][m - 1];
    }
public:
    //Function to find the maximum cherries collected
    int cherryPickup(vector<vector<int>> &matrix){
        int n = matrix.size();
        int m = matrix[0].size();
        
        //Return the answer
        return func(n, m, matrix);
    }
};
int main() {
    vector<vector<int>> matrix{
        {2, 3, 1, 2},
        {3, 4, 2, 2},
        {5, 6, 3, 5},
    };
    
    //Create an instance of Solution class
    Solution sol;

    // Call the maximumChocolates function and print the result
    cout << sol.cherryPickup(matrix);

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the maximum cherries that
    can be collected using space optimization*/
    int func(int n, int m, int[][] matrix) {
        /* Declare two 2D arrays 'front' and 
        'cur' to store computed results*/
        int[][] front = new int[m][m];
        int[][] cur = new int[m][m];

        // Initialize 'front' for the last row
        for (int j1 = 0; j1 < m; j1++) {
            for (int j2 = 0; j2 < m; j2++) {
                if (j1 == j2)
                    front[j1][j2] = matrix[n - 1][j1];
                else
                    front[j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2];
            }
        }

        /* Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row*/
        for (int i = n - 2; i >= 0; i--) {
            for (int j1 = 0; j1 < m; j1++) {
                for (int j2 = 0; j2 < m; j2++) {
                    int maxi = Integer.MIN_VALUE;

                    // Inner nested loops to try out 9 options
                    for (int di = -1; di <= 1; di++) {
                        for (int dj = -1; dj <= 1; dj++) {
                            int ans;

                            if (j1 == j2)
                                ans = matrix[i][j1];
                            else
                                ans = matrix[i][j1] + matrix[i][j2];

                            // Check if the move is valid
                            if ((j1 + di < 0 || j1 + di >= m) || (j2 + dj < 0 || j2 + dj >= m))
                                /* A very large negative value
                                to represent an invalid move*/
                                ans += -1e9;
                            else
                                ans += front[j1 + di][j2 + dj];

                            // Update the maximum result
                            maxi = Math.max(ans, maxi);
                        }
                    }
                    /* Store the maximum result for 
                    this state in the 'cur' array*/
                    cur[j1][j2] = maxi;
                }
            }
            /* Update 'front' with the values 
            from 'cur' for the next iteration*/
            for (int j1 = 0; j1 < m; j1++) {
                for (int j2 = 0; j2 < m; j2++) {
                    front[j1][j2] = cur[j1][j2];
                }
            }
        }

        /* The maximum cherries that can be collected is
        stored at the top-left corner of the 'front'*/
        return front[0][m - 1];
    }

    // Function to find the maximum cherries collected
    int cherryPickup(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;

        // Return the answer
        return func(n, m, matrix);
    }

    public static void main(String[] args) {
        int[][] matrix = {{2, 3, 1, 2},
                          {3, 4, 2, 2},
                          {5, 6, 3, 5}};

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the cherryPickup function and print the result
        System.out.println(sol.cherryPickup(matrix)); 
    }
}
import copy

class Solution:
    """ Function to find the maximum cherries that
    can be collected using space optimization"""
    def func(self, n, m, matrix):
        """ Declare two 2D lists 'front' and
        'cur' to store computed results"""
        front = [[0]*m for _ in range(m)]
        cur = [[0]*m for _ in range(m)]

        # Initialize 'front' for the last row
        for j1 in range(m):
            for j2 in range(m):
                if j1 == j2:
                    front[j1][j2] = matrix[n - 1][j1]
                else:
                    front[j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2]

        """ Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row"""
        for i in range(n - 2, -1, -1):
            for j1 in range(m):
                for j2 in range(m):
                    maxi = float('-inf')

                    # Inner nested loops to try out 9 options
                    for di in [-1, 0, 1]:
                        for dj in [-1, 0, 1]:
                            if 0 <= j1 + di < m and 0 <= j2 + dj < m:
                                ans = matrix[i][j1]
                                if j1 != j2:
                                    ans += matrix[i][j2]
                                ans += front[j1 + di][j2 + dj]
                            else:
                                """ A very large negative 
                                value for invalid moves"""
                                ans = -1e9  

                            maxi = max(maxi, ans)

                    """ Store the maximum result for
                    this state in the 'cur' array"""
                    cur[j1][j2] = maxi

            """ Update 'front' with the values 
            from 'cur' for the next iteration"""
            front = copy.deepcopy(cur)

        """ The maximum cherries that can be collected 
        is stored at the top-left corner of the 'front'"""
        return front[0][m - 1]

    # Function to find the maximum cherries collected
    def cherryPickup(self, matrix):
        n = len(matrix)
        m = len(matrix[0])

        # Return the answer
        return self.func(n, m, matrix)

if __name__ == "__main__":
    matrix = [
        [2, 3, 1, 2],
        [3, 4, 2, 2],
        [5, 6, 3, 5]
    ]

    # Create an instance of Solution class
    sol = Solution()

    # Call the cherryPickup function and print the result
    print(sol.cherryPickup(matrix)) 
class Solution {
    /* Function to find the maximum cherries 
    that can be collected using space optimization*/
    func(n, m, matrix) {
        /* Declare two 2D arrays 'front' and
        'cur' to store computed results*/
        let front = new Array(m);
        let cur = new Array(m);
        for (let i = 0; i < m; i++) {
            front[i] = new Array(m).fill(0);
            cur[i] = new Array(m).fill(0);
        }

        // Initialize 'front' for the last row
        for (let j1 = 0; j1 < m; j1++) {
            for (let j2 = 0; j2 < m; j2++) {
                if (j1 === j2)
                    front[j1][j2] = matrix[n - 1][j1];
                else
                    front[j1][j2] = matrix[n - 1][j1] + matrix[n - 1][j2];
            }
        }

        /* Outer nested loops for traversing the DP array
        from the second-to-last row up to the first row*/
        for (let i = n - 2; i >= 0; i--) {
            for (let j1 = 0; j1 < m; j1++) {
                for (let j2 = 0; j2 < m; j2++) {
                    let maxi = Number.MIN_SAFE_INTEGER;

                    // Inner nested loops to try out 9 options
                    for (let di = -1; di <= 1; di++) {
                        for (let dj = -1; dj <= 1; dj++) {
                            let ans;

                            if (j1 === j2)
                                ans = matrix[i][j1];
                            else
                                ans = matrix[i][j1] + matrix[i][j2];

                            // Check if the move is valid
                            if (
                                j1 + di >= 0 && j1 + di < m &&
                                j2 + dj >= 0 && j2 + dj < m
                            ) {
                                ans += front[j1 + di][j2 + dj];
                            } else {
                                /* A very large negative
                                value for invalid moves*/
                                ans += -1e9; 
                            }

                            // Update the maximum result
                            maxi = Math.max(ans, maxi);
                        }
                    }

                    /* Store the maximum result for
                    this state in the 'cur' array*/
                    cur[j1][j2] = maxi;
                }
            }

            /* Update 'front' with the values 
            from 'cur' for the next iteration*/
            for (let j = 0; j < m; j++) {
                front[j] = cur[j].slice();
            }
        }

        /* The maximum cherries that can be collected is
        stored at the top-left corner of the 'front'*/
        return front[0][m - 1];
    }

    // Function to find the maximum cherries collected
    cherryPickup(matrix) {
        let n = matrix.length;
        let m = matrix[0].length;

        // Return the answer
        return this.func(n, m, matrix);
    }
}

const matrix = [[2, 3, 1, 2],
                [3, 4, 2, 2],
                [5, 6, 3, 5]];

    // Create an instance of Solution class
    const sol = new Solution();

    // Call the cherryPickup function and print the result
    console.log(sol.cherryPickup(matrix));
   

Complexity Analysis:

Time Complexity: O((N*M*M)*9), The outer nested loops run for (N*M*M) times and the inner two nested loops run for 9 times

Space Complexity:O(M*M). As an external array of size ‘M*M’ is used.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Why Greedy Approach will not work:

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

The Steps to space optimize the tabulation approach are as follows:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code