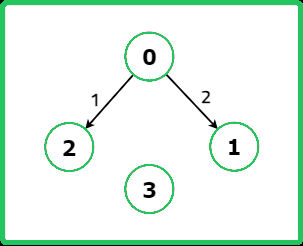
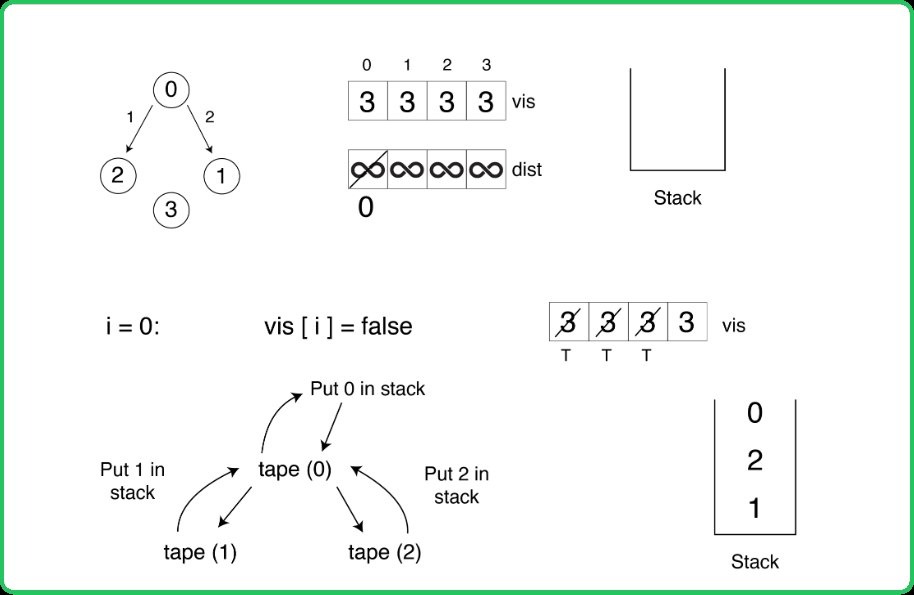
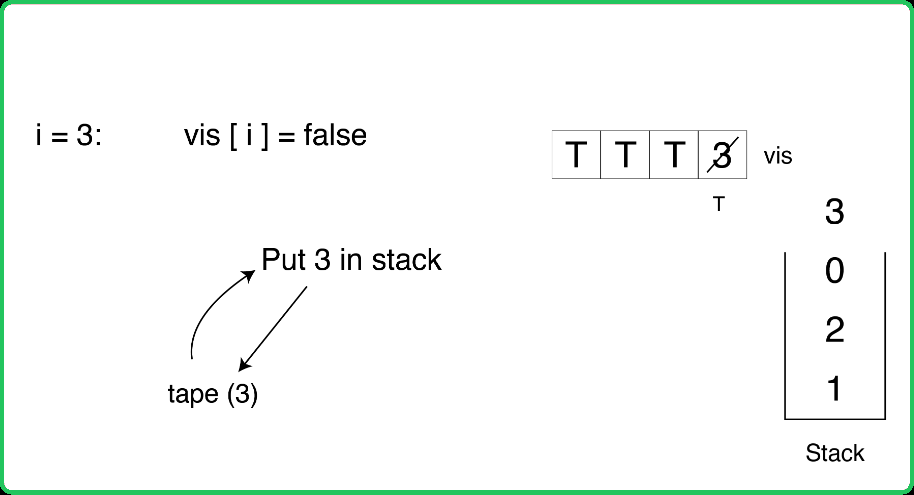
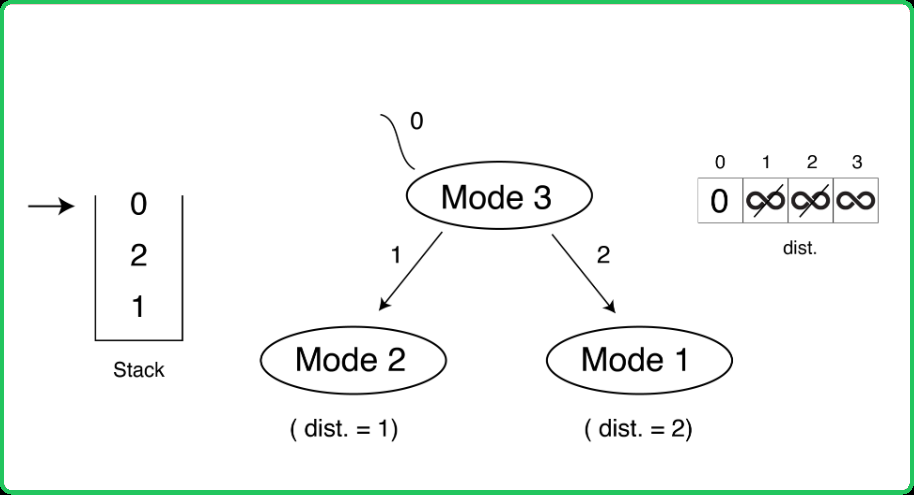
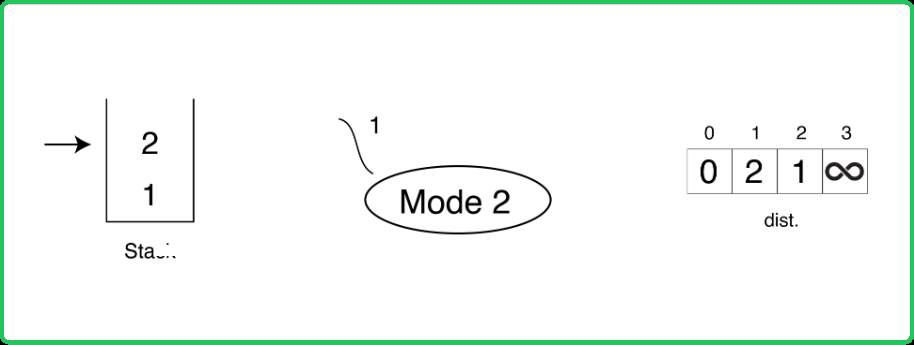
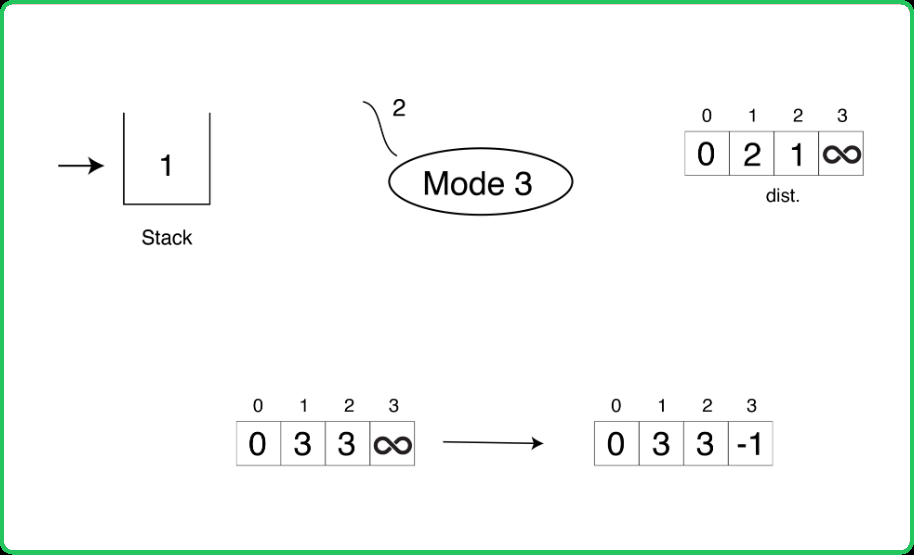
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
// Function to perform DFS traversal
void topoSort(int node, vector <pair<int,int>> adj[],
vector<bool> &vis, stack <int> & st) {
// Mark the node as visited
vis[node] = 1;
// Traverse all the neighbors
for (auto it: adj[node]) {
// Get the node
int v = it.first;
// If not visited, recursively perform DFS.
if (!vis[v]) {
topoSort(v, adj, vis, st);
}
}
/* Add the current node to stack
once all the nodes connected to it
have been processed */
st.push(node);
}
public:
/* Function to get the shortest path
for every node from source node 0 */
vector<int> shortestPath(int N, int M,
vector<vector<int>> &edges) {
// To store the graph
vector <pair<int,int>> adj[N];
// Add edges to the graph
for (int i = 0; i < M; i++) {
int u = edges[i][0]; // node 1
int v = edges[i][1]; // node 2
int wt = edges[i][2]; // edge weight
// Add the weighted edge
adj[u].push_back({v, wt});
}
// Visited array
vector<bool> vis(N, false);
/* Stack to facilitate topological
sorting using DFS traversal */
stack <int> st;
// Get the topological ordering
for (int i = 0; i < N; i++) {
if (!vis[i]) {
topoSort(i, adj, vis, st);
}
}
// Distance array to store the shortest paths
vector <int> dist(N, 1e9);
// Distance of source node to itself is zero
dist[0] = 0;
// Until the stack is not empty
while (!st.empty()) {
// Get the node from top of stack
int node = st.top();
st.pop();
// Update the distances of adjacent nodes
for (auto it: adj[node]) {
int v = it.first; // adjacent node
int wt = it.second; // edge weight
/* Relaxing the edge, i.e., if a
shorter path is found, update its
distance to new shorter distance*/
if (dist[node] + wt < dist[v]) {
dist[v] = wt + dist[node];
}
}
}
/* If a node is unreachable,
updating its distance to -1 */
for (int i = 0; i < N; i++) {
if (dist[i] == 1e9)
dist[i] = -1;
}
// Return the result
return dist;
}
};
int main() {
int N = 4, M = 2;
vector<vector<int>> edges = {
{0, 1, 2}, {0, 2, 1}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to determine order of
letters based on alien dictionary */
vector<int> ans = sol.shortestPath(N, M, edges);
// Output
cout << "The shortest distance of every node from source node is:\n";
for(int i=0; i < N; i++) {
cout << ans[i] << " ";
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130
import java.util.*;
class Solution {
// Pair implementation
static class Pair {
int first, second;
Pair(int first, int second) {
this.first = first;
this.second = second;
}
}
private void topoSort(int node, List<List<Pair>> adj,
boolean[] vis, Stack<Integer> st) {
// Mark the node as visited
vis[node] = true;
// Traverse all the neighbors
for (Pair it : adj.get(node)) {
// Get the node
int v = it.first;
// If not visited, recursively perform DFS
if (!vis[v]) {
topoSort(v, adj, vis, st);
}
}
/* Add the current node to stack
once all the nodes connected to it
have been processed */
st.push(node);
}
public int[] shortestPath(int N, int M, int[][] edges) {
// To store the graph
List<List<Pair>> adj = new ArrayList<>();
for (int i = 0; i < N; i++) {
adj.add(new ArrayList<>());
}
// Add edges to the graph
for (int i = 0; i < M; i++) {
int u = edges[i][0]; // node 1
int v = edges[i][1]; // node 2
int wt = edges[i][2]; // edge weight
// Add the weighted edge
adj.get(u).add(new Pair(v, wt));
}
// Visited array
boolean[] vis = new boolean[N];
/* Stack to facilitate topological
sorting using DFS traversal */
Stack<Integer> st = new Stack<>();
// Get the topological ordering
for (int i = 0; i < N; i++) {
if (!vis[i]) {
topoSort(i, adj, vis, st);
}
}
// Distance array to store the shortest paths
int[] dist = new int[N];
Arrays.fill(dist, (int)1e9);
// Distance of source node to itself is zero
dist[0] = 0;
// Until the stack is not empty
while (!st.isEmpty()) {
// Get the node from top of stack
int node = st.pop();
// Update the distances of adjacent nodes
for (Pair it : adj.get(node)) {
int v = it.first; // adjacent node
int wt = it.second; // edge weight
/* Relaxing the edge, i.e., if a
shorter path is found, update its
distance to new shorter distance */
if (dist[node] + wt < dist[v]) {
dist[v] = wt + dist[node];
}
}
}
/* If a node is unreachable,
updating its distance to -1 */
for (int i = 0; i < N; i++) {
if (dist[i] == (int)1e9)
dist[i] = -1;
}
// Return the result
return dist;
}
}
class Main {
public static void main(String[] args) {
int N = 4, M = 2;
int[][] edges = {
{0, 1, 2}, {0, 2, 1}
};
// Creating an instance of Solution class
Solution sol = new Solution();
// Function call to determine order of
// letters based on alien dictionary
int[] ans = sol.shortestPath(N, M, edges);
// Output
System.out.println("The shortest distance of every node from source node is:");
for (int i : ans) {
System.out.print(i + " ");
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293
from collections import defaultdict
from typing import List
class Solution:
# Function to perform DFS traversal
def topoSort(self, node, adj, vis, st):
# Mark the node as visited
vis[node] = True
# Traverse all the neighbors
for v, _ in adj[node]:
# If not visited, recursively perform DFS
if not vis[v]:
self.topoSort(v, adj, vis, st)
""" Add the current node to stack
once all the nodes connected to it
have been processed """
st.append(node)
# Function to get the shortest path
# for every node from source node 0
def shortestPath(self, N, M, edges):
# To store the graph
adj = defaultdict(list)
# Add edges to the graph
for u, v, wt in edges:
# Add the weighted edge
adj[u].append((v, wt))
# Visited array
vis = [False] * N
""" Stack to facilitate topological
sorting using DFS traversal """
st = []
# Get the topological ordering
for i in range(N):
if not vis[i]:
self.topoSort(i, adj, vis, st)
# Distance array to store the shortest paths
dist = [1e9] * N
# Distance of source node to itself is zero
dist[0] = 0
# Until the stack is not empty
while st:
# Get the node from top of stack
node = st.pop()
# Update the distances of adjacent nodes
for v, wt in adj[node]:
""" Relaxing the edge, i.e., if a
shorter path is found, update its
distance to new shorter distance """
if dist[node] + wt < dist[v]:
dist[v] = wt + dist[node]
""" If a node is unreachable,
updating its distance to -1 """
for i in range(N):
if dist[i] == 1e9:
dist[i] = -1
# Return the result
return dist
# Example usage
N, M = 4, 2
edges = [
[0, 1, 2], [0, 2, 1]
]
# Creating an instance of Solution class
sol = Solution()
# Function call to determine order of
# letters based on alien dictionary
ans = sol.shortestPath(N, M, edges)
# Output
print("The shortest distance of every node from source node is:")
print(*ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113
class Solution {
// Function to perform DFS traversal
topoSort(node, adj, vis, st) {
// Mark the node as visited
vis[node] = true;
// Traverse all the neighbors
for (let it of adj[node]) {
// Get the node
let v = it[0];
// If not visited, recursively perform DFS.
if (!vis[v]) {
this.topoSort(v, adj, vis, st);
}
}
/* Add the current node to stack
once all the nodes connected to it
have been processed */
st.push(node);
}
/* Function to get the shortest path
for every node from source node 0 */
shortestPath(N, M, edges) {
// To store the graph
let adj = Array.from({ length: N }, () => []);
// Add edges to the graph
for (let i = 0; i < M; i++) {
let u = edges[i][0]; // node 1
let v = edges[i][1]; // node 2
let wt = edges[i][2]; // edge weight
// Add the weighted edge
adj[u].push([v, wt]);
}
// Visited array
let vis = new Array(N).fill(false);
/* Stack to facilitate topological
sorting using DFS traversal */
let st = [];
// Get the topological ordering
for (let i = 0; i < N; i++) {
if (!vis[i]) {
this.topoSort(i, adj, vis, st);
}
}
// Distance array to store the shortest paths
let dist = new Array(N).fill(1e9);
// Distance of source node to itself is zero
dist[0] = 0;
// Until the stack is not empty
while (st.length > 0) {
// Get the node from top of stack
let node = st.pop();
// Update the distances of adjacent nodes
for (let it of adj[node]) {
let v = it[0]; // adjacent node
let wt = it[1]; // edge weight
/* Relaxing the edge, i.e., if a
shorter path is found, update its
distance to new shorter distance*/
if (dist[node] + wt < dist[v]) {
dist[v] = wt + dist[node];
}
}
}
/* If a node is unreachable,
updating its distance to -1 */
for (let i = 0; i < N; i++) {
if (dist[i] === 1e9)
dist[i] = -1;
}
// Return the result
return dist;
}
}
// Example usage
let N = 4, M = 2;
let edges = [
[0, 1, 2], [0, 2, 1]
];
// Creating an instance of Solution class
let sol = new Solution();
// Function call to determine order of letters based on alien dictionary
let ans = sol.shortestPath(N, M, edges);
// Output
console.log("The shortest distance of every node from source node is:");
for (let i = 0; i < N; i++) {
console.log(ans[i] + " ");
}