Shortest common supersequence

Intuition:

If we keep the “shortest” criteria aside, what can be a way to generate a supersequence given two strings. One easy way is to concat the given strings (write one after the other), this will always give us a supersequence for any pair of given strings.

This can be said as the worst case with time complexity of O(n+m), where n and are the lengths of strings str1 and str2 respectively.

How can we improve the naive approach:

If we observe, there are some common characters that we can avoid writing for both the strings separately. These common characters can’t be all the common characters. They are the characters that are common and come in the same order. In other words, they are the characters of the longest common subsequence.

In an optimum solution, the characters of the longest common subsequence are written only once and other characters are placed around them. For every character that belongs to the longest common subsequence, the non-lcs characters coming before them in the strings S1 and S2 are placed before the lcs-character in the answer string. The below figure explains this:

Length of Shortest Common Supersequence(lcs):

From the explanation above, we can see that characters of lcs need to be covered only once. Therefore, the length of the shortest Common supersequence = n + m -k, where (n and m are lengths of str1 and str2, and k is the length of the lcs string).

Finding the supersequence string:

Now, instead of the length, we are interested in finding the shortest supersequence string itself.

When we form the DP table to calculate the longest common subsequence, we have all the information of characters that are coming in the lcs string and characters that don’t. We use this same DP table to form the shortest common supersequence.

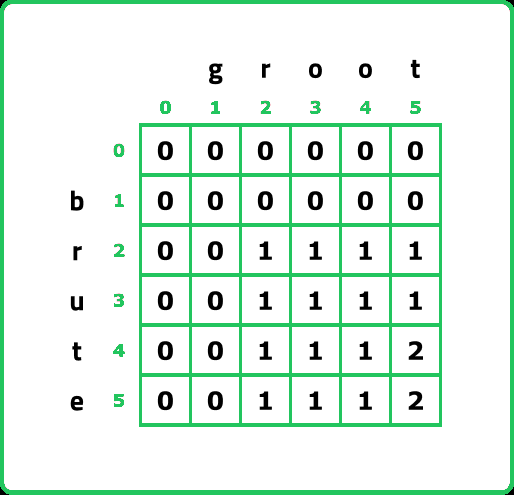
To frame the string, we need to understand how the dp table was formed and work in the reverse process.

Now, let us see what were the conditions that we used while forming the dp array:

If(str1[i-1] == str2[j-1]), then return 1 + dp[i-1][j-1]
If(str1[i-1] != str22[j-1]) , then return 0 + max(dp[i-1][j],dp[i][j-1])

Approach:

We will start from the right-most cell of the dp array, initially i=n and j=m. To form the string, we will work in a reverse manner.

If(str1[i-1] == str2[j-1]), this means the character is an lcs character and needs to be included only once from both the strings, so we add it to the ans string and reduce both i and j by 1. We reduce them simultaneously to make sure the character is counted only once.
If(str1[i-1] != str2[j-1]), this means that the character is a non-lcs character and then we move the pointer to the top cell or left cell depending on which is greater. This way non-lcs characters will be included separately in the right order.

The algorithm steps are stated below:

At every cell, we will check if S1[i-1] == S2[j-1], if it is then it means this character is a part of the longest common subsequence. So we will push it to the ans string str. Then we will move to the diagonally top-left(↖) cell by assigning i to i-1 and j to j-1.
Else, this character is not a part of the longest common subsequence so we include it in ans string. Originally this cell got its value from its left cell (←) or from its top cell (↑). Whichever cell’s value will be more of the two, we will move to that cell.
We will continue till i>0 and j>0, failing it we will break from the loop.
After breaking, either i>0 or j>0 (only one condition will fail to break from the while loop), if(i>0) we push all the characters from S1 to ans string, else if(j>0), we push all the remaining characters from S2.
At last, we reverse the ‘ans’ string and we get our answer.

Dry Run:

In the beginning i=5 and j=5.

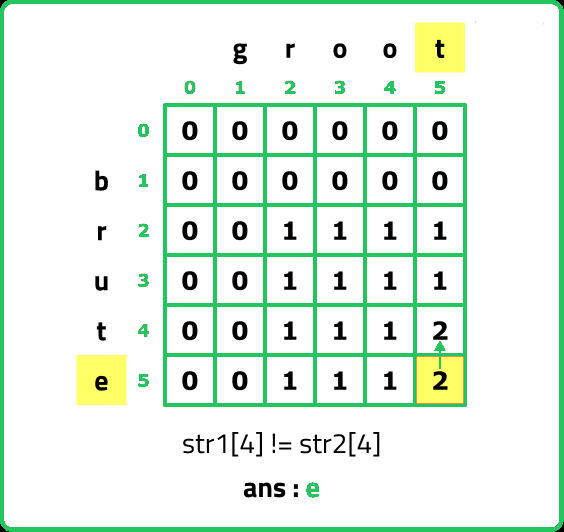
As S1[4] != S2[4], we move to the top cell(↑) as its value is greater than the left cell(←) but before moving as we are leaving row 5(i=5) and will not return to it so we add S1[4] to our ans string.

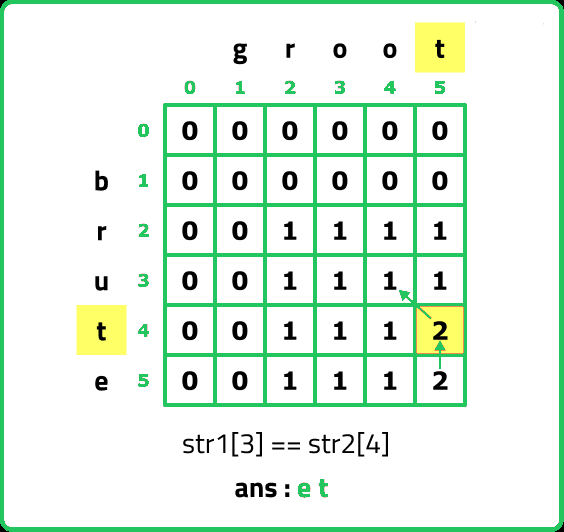
As S1[3] == S2[4], this is an lcs-character. We add the current character to the ans string(and move to i-1 and j-1 cell) i.e top-left(↖). Reducing i and j simultaneously helps in adding the lcs character only once in the ans string.

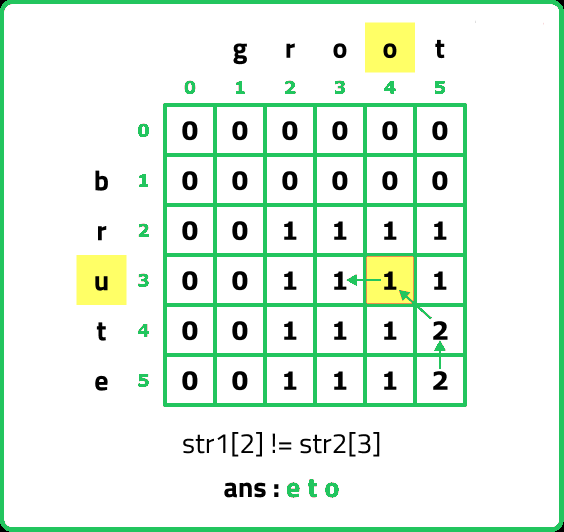
As S1[2] != S2[3], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 4 (j=4) and will not return to it so we add S2[3] to our ans string.

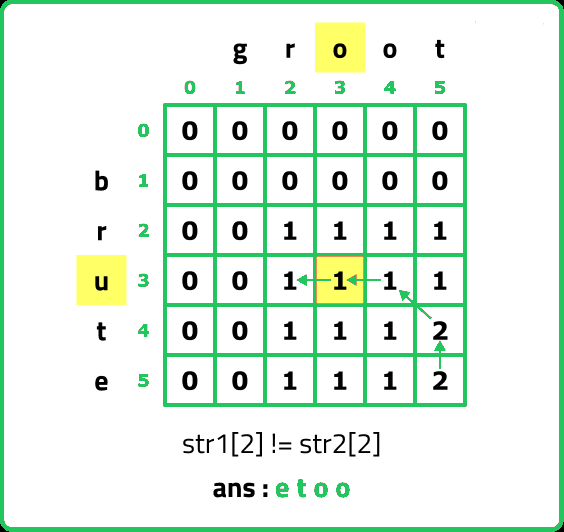
As S1[2] != S2[2], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 3 (j=3) and will not return to it so we add S2[2] to our ans string.

As S1[2] != S2[1], we move to the top cell(↑) as its value is greater than the left cell(←) but before moving as we are leaving row 3(i=3) and will not return to it so we add S1[2] to our ans string.

As S1[1] == S2[1], this is an lcs-character. We add the current character to the ans string(and move to i-1 and j-1 cell) i.e top-left(↖).

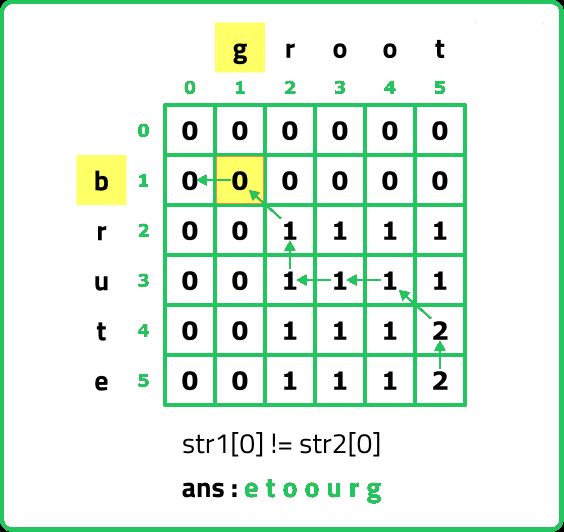
As S1[2] != S2[2], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 1 (j=1) and will not return to it so we add S2[0] to our ans string.

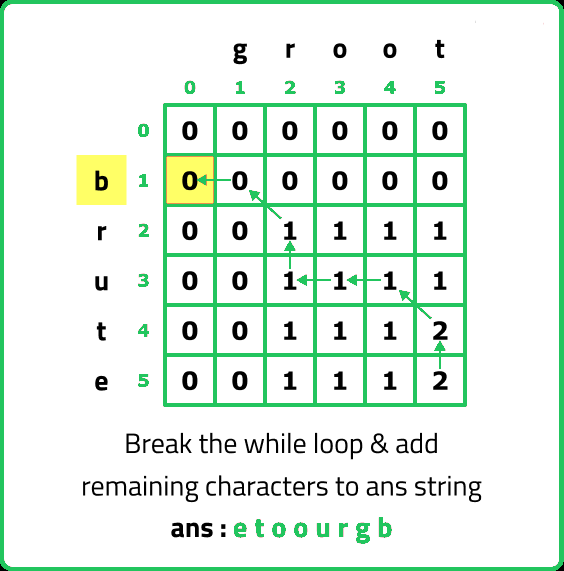
As j=0, we have reached the exit condition of the while loop, so we will break from it but still there are some characters left in the other string. We will simply add them in the ans string.
At last, we will return the reverse of the ans string as the final answer.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    //Function to fund the shortest common supersequence
    string shortestCommonSupersequence(string str1, string str2) {
        int n = str1.size();
        int m = str2.size();

        // Create a DP table with dimensions (n+1) x (m+1) initialized to 0
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));

        // Initialize the first row and column of the DP table
        for (int i = 0; i <= n; i++) {
            dp[i][0] = 0;
        }
        for (int i = 0; i <= m; i++) {
            dp[0][i] = 0;
        }

        // Fill the DP table
        for (int ind1 = 1; ind1 <= n; ind1++) {
            for (int ind2 = 1; ind2 <= m; ind2++) {
                if (str1[ind1 - 1] == str2[ind2 - 1])
                    dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1]; 
                else
                    dp[ind1][ind2] = max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]); 
            }
        }

        // Reconstruct the shortest supersequence from the DP table
        int len = dp[n][m];
        int i = n;
        int j = m;

        int index = len - 1;
        string ans = "";

        // Build the shortest supersequence by backtracking
        while (i > 0 && j > 0) {
            if (str1[i - 1] == str2[j - 1]) {
                ans += str1[i - 1]; 
                index--;
                i--;
                j--;
            } else if (dp[i - 1][j] > dp[i][j - 1]) {
                ans += str1[i - 1]; 
                i--;
            } else {
                ans += str2[j - 1]; 
                j--;
            }
        }

        // Add remaining characters from str1 or str2
        while (i > 0) {
            ans += str1[i - 1];
            i--;
        }
        while (j > 0) {
            ans += str2[j - 1];
            j--;
        }

        // Reverse the result since we built it backwards
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

int main() {
    string s1 = "brute";
    string s2 = "groot";
    
    // Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The Longest Common Supersequence is " << sol.shortestCommonSupersequence(s1, s2);
}
import java.util.*;

class Solution {
    // Function to find the shortest common supersequence
    public String shortestCommonSupersequence(String str1, String str2) {
        int n = str1.length();
        int m = str2.length();

        // Create a DP table initialized to 0
        int[][] dp = new int[n + 1][m + 1];

        // Initialize the first row and column of DP table
        for (int i = 0; i <= n; i++) {
            dp[i][0] = 0;
        }
        for (int i = 0; i <= m; i++) {
            dp[0][i] = 0;
        }

        // Fill the DP table
        for (int ind1 = 1; ind1 <= n; ind1++) {
            for (int ind2 = 1; ind2 <= m; ind2++) {
                if (str1.charAt(ind1 - 1) == str2.charAt(ind2 - 1))
                    dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1];
                else
                    dp[ind1][ind2] = Math.max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]);
            }
        }

        // Reconstruct the shortest supersequence from DP table
        int len = dp[n][m];
        int i = n;
        int j = m;

        int index = len - 1;
        StringBuilder ans = new StringBuilder();

        // Build the shortest supersequence by backtracking
        while (i > 0 && j > 0) {
            if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
                ans.append(str1.charAt(i - 1));
                index--;
                i--;
                j--;
            } else if (dp[i - 1][j] > dp[i][j - 1]) {
                ans.append(str1.charAt(i - 1));
                i--;
            } else {
                ans.append(str2.charAt(j - 1));
                j--;
            }
        }

        // Add remaining characters from str1 or str2
        while (i > 0) {
            ans.append(str1.charAt(i - 1));
            i--;
        }
        while (j > 0) {
            ans.append(str2.charAt(j - 1));
            j--;
        }

        // Reverse the result since we built it backwards
        ans.reverse();
        return ans.toString();
    }

    public static void main(String[] args) {
        String s1 = "brute";
        String s2 = "groot";

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The Longest Common Supersequence is " + sol.shortestCommonSupersequence(s1, s2));
    }
}
class Solution:
    # Function to find the shortest common supersequence
    def shortestCommonSupersequence(self, str1, str2):
        n = len(str1)
        m = len(str2)

        # Create a DP table initialized to 0
        dp = [[0] * (m + 1) for _ in range(n + 1)]

        # Initialize the first row and column of the DP table
        for i in range(n + 1):
            dp[i][0] = 0
        for i in range(m + 1):
            dp[0][i] = 0

        # Fill the DP table
        for ind1 in range(1, n + 1):
            for ind2 in range(1, m + 1):
                if str1[ind1 - 1] == str2[ind2 - 1]:
                    dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1]
                else:
                    dp[ind1][ind2] = max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1])

        # Reconstruct the shortest supersequence from DP table
        len_superseq = dp[n][m]
        i = n
        j = m

        index = len_superseq - 1
        ans = []

        # Build the shortest supersequence by backtracking
        while i > 0 and j > 0:
            if str1[i - 1] == str2[j - 1]:
                ans.append(str1[i - 1])
                index -= 1
                i -= 1
                j -= 1
            elif dp[i - 1][j] > dp[i][j - 1]:
                ans.append(str1[i - 1])
                i -= 1
            else:
                ans.append(str2[j - 1])
                j -= 1

        # Add remaining characters from str1 or str2
        while i > 0:
            ans.append(str1[i - 1])
            i -= 1
        while j > 0:
            ans.append(str2[j - 1])
            j -= 1

        # Reverse the result since we built it backwards
        ans.reverse()
        return ''.join(ans)

s1 = "brute"
s2 = "groot"

# Create an instance of Solution class
sol = Solution()

# Print the result
print(f"The Longest Common Supersequence is {sol.shortestCommonSupersequence(s1, s2)}")
class Solution {
    // Function to find the shortest common supersequence
    shortestCommonSupersequence(str1, str2) {
        let n = str1.length;
        let m = str2.length;

        // Create a DP table initialized to 0
        let dp = Array.from({ length: n + 1 }, () => Array(m + 1).fill(0));

        // Initialize the first row and column of DP table
        for (let i = 0; i <= n; i++) {
            dp[i][0] = 0;
        }
        for (let i = 0; i <= m; i++) {
            dp[0][i] = 0;
        }

        // Fill the DP table
        for (let ind1 = 1; ind1 <= n; ind1++) {
            for (let ind2 = 1; ind2 <= m; ind2++) {
                if (str1[ind1 - 1] === str2[ind2 - 1])
                    dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1];
                else
                    dp[ind1][ind2] = Math.max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]);
            }
        }

        // Reconstruct the shortest supersequence from DP table
        let len = dp[n][m];
        let i = n;
        let j = m;

        let index = len - 1;
        let ans = "";

        // Build the shortest supersequence by backtracking
        while (i > 0 && j > 0) {
            if (str1[i - 1] === str2[j - 1]) {
                ans += str1[i - 1];
                index--;
                i--;
                j--;
            } else if (dp[i - 1][j] > dp[i][j - 1]) {
                ans += str1[i - 1];
                i--;
            } else {
                ans += str2[j - 1];
                j--;
            }
        }

        // Add remaining characters from str1 or str2
        while (i > 0) {
            ans += str1[i - 1];
            i--;
        }
        while (j > 0) {
            ans += str2[j - 1];
            j--;
        }

        // Reverse the result since we built it backwards
        return ans.split('').reverse().join('');
    }
}

let s1 = "brute";
let s2 = "groot";

// Create an instance of Solution class
let sol = new Solution();

// Print the result
console.log("The Longest Common Supersequence is " + sol.shortestCommonSupersequence(s1, s2));

Complexity Analysis:

Time Complexity: O(N*M), Where N is the length of string str1 and M is the length of string str2. As there are two nested loops, the time complexity will be O(N*M).

Space Complexity: O(N*M), We are using an external array of size (N*M).

Problem List

Shortest common supersequence

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

How can we improve the naive approach:

Length of Shortest Common Supersequence(lcs):

Finding the supersequence string:

Approach:

The algorithm steps are stated below:

Dry Run:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code