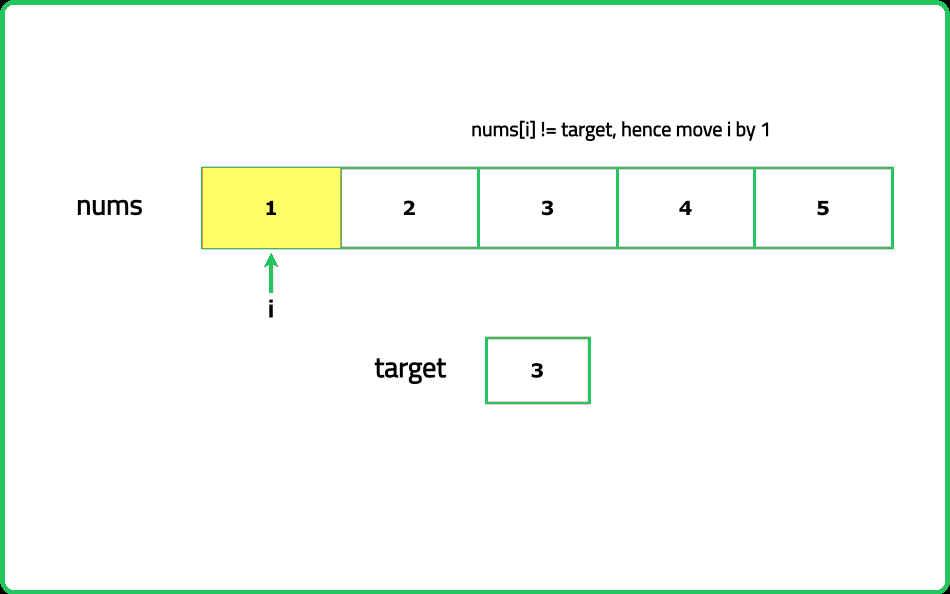
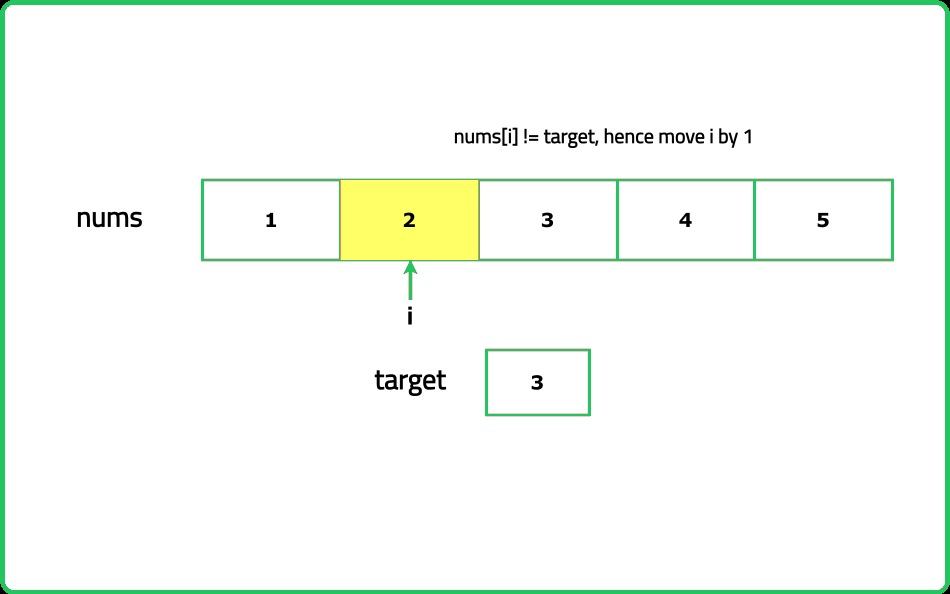
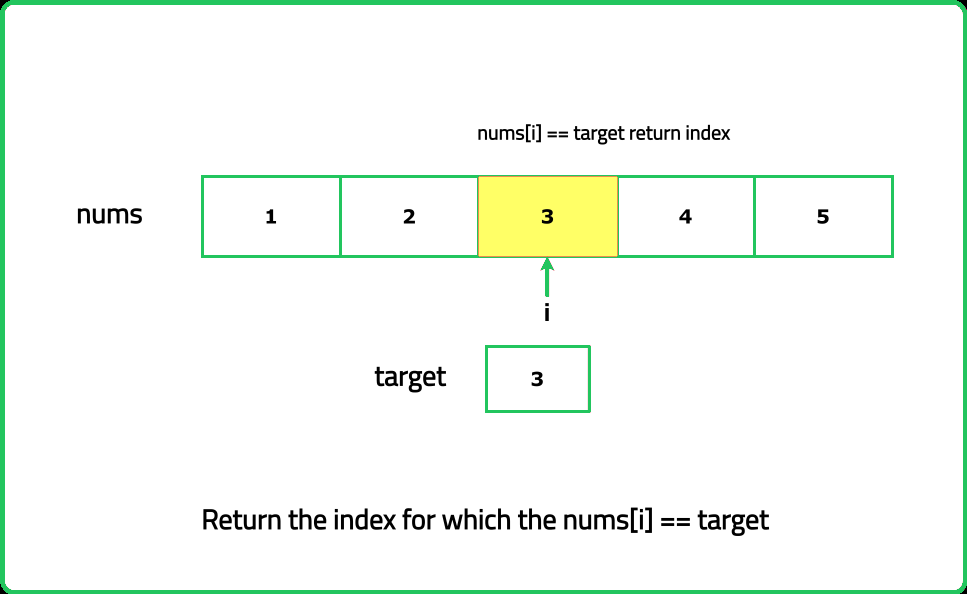
Linear Search
Given an array of integers nums and an integer target, find the smallest index (0 based indexing) where the target appears in the array. If the target is not found in the array, return -1
Examples:
Input: nums = [2, 3, 4, 5, 3], target = 3
Output: 1
Explanation: The first occurence of 3 in nums is at index 1
Input: nums = [2, -4, 4, 0, 10], target = 6
Output: -1
Explanation: The value 6 does not occur in the array, hence output is -1
Input: nums = [1, 3, 5, -4, 1], target = 1
Constraints
- 1 <= nums.length <= 105
- -104 <= nums[i] <= 104
- -104 <= target <= 104
Hints
- Start at the first element and compare it with the target. Continue until you find the target or reach the end of the array. Ensure to stop searching and return the index as soon as the target is found, as you are looking for the smallest index.
- Remember to handle edge cases where the target is at the beginning or end of the array, or if it is not present at all.
Company Tags
Reddit
Texas Instruments
Qualcomm
Swiggy
American Express
Zomato
Roblox
Red Hat
Lyft
Ubisoft
HCL Technologies
GE Healthcare
Roche
Oracle
AMD
Byju's
Dropbox
KPMG
Deloitte
Epic Games
Goldman Sachs
Splunk
Intel
McKinsey & Company
Flipkart
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro