Bubble Sort
Sorting
Algorithms
Easy
- Although bubble sort is widely regarded as inefficient for large datasets due to its worst-case and average time complexity of O(n²), it is popular in teaching introductory computer science courses, both for its simplicity and because it performs well in scenarios with small and nearly sorted datasets
- Some software testing and debugging tools, especially those maintaining watchlists or logs, may make use of bubble sort where the expected input size isn't large but the order is crucial for correct interpretation of results
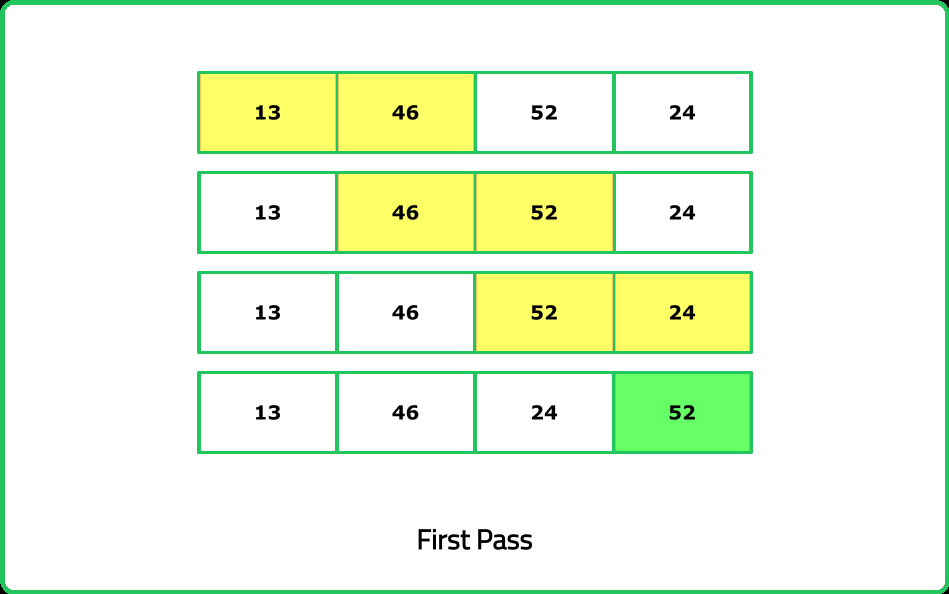
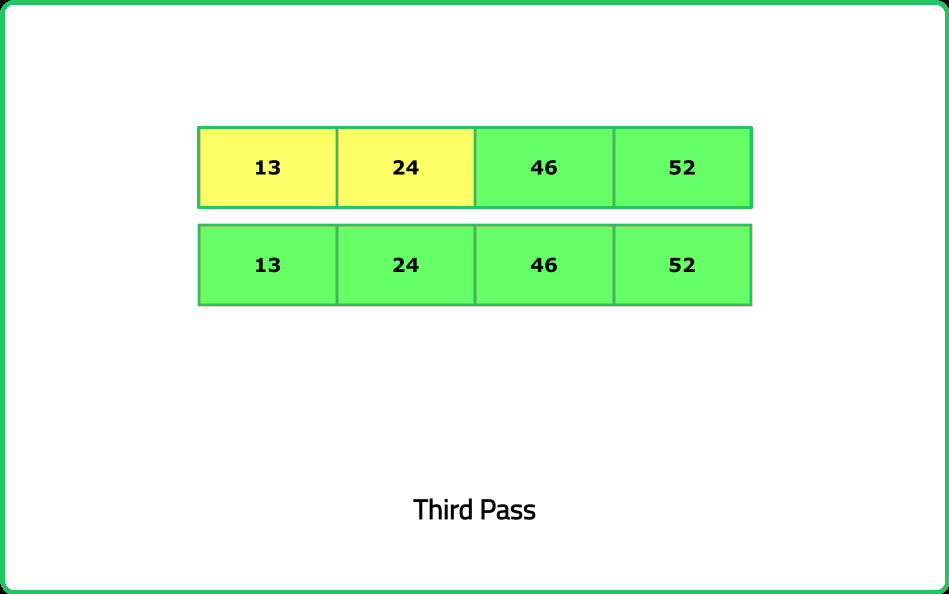
Given an array of integers called nums,sort the array in non-decreasing order using the bubble sort algorithm and return the sorted array.
A sorted array in non-decreasing order is an array where each element is greater than or equal to all preceding elements in the array.
Examples:
Input: nums = [7, 4, 1, 5, 3]
Output: [1, 3, 4, 5, 7]
Explanation: 1 <= 3 <= 4 <= 5 <= 7.
Thus the array is sorted in non-decreasing order.
Input: nums = [5, 4, 4, 1, 1]
Output: [1, 1, 4, 4, 5]
Explanation: 1 <= 1 <= 4 <= 4 <= 5.
Thus the array is sorted in non-decreasing order.
Input: nums = [3, 2, 3, 4, 5]
Constraints
- 1 <= nums.length <= 1000
- -104 <= nums[i] <= 104
- nums[i] may contain duplicate values.
Hints
- Focus on comparing adjacent elements and swapping them if they are in the wrong order. Repeat this until no swaps are needed. After each iteration, the largest element in the unsorted portion moves to its correct position at the end.
- For Optimization, Think about stopping the algorithm early if no swaps occur during an iteration, indicating the array is already sorted.
Company Tags
AMD
Flipkart
PayPal
ARM
Goldman Sachs
Zomato
Micron Technology
Philips Healthcare
Shopify
Intel
Morgan Stanley
Cloudflare
JPMorgan Chase
Roblox
Broadcom
Target
Square
Bungie
Swiggy
IBM
KPMG
DoorDash
OYO Rooms
Nutanix
Ubisoft
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro