123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144
#include <bits/stdc++.h>
using namespace std;
/* Define P as a shorthand
for the pair<int, int> type */
#define P pair<int,int>
class Solution {
public:
/* Function to find the shortest
path from node 1 to node n */
vector<int> shortestPath(int n, int m,
vector<vector<int>> &edges) {
// Adjacency list to store graph
vector<pair<int, int>> adj[n + 1];
// Adding the edges to the graph
for (auto it : edges) {
adj[it[0]].push_back({it[1], it[2]});
adj[it[1]].push_back({it[0], it[2]});
}
/* Using priority queue to
implement Dijkstra Algorithm */
priority_queue<P, vector<P>, greater<P>> pq;
// Distance array
vector<int> dist(n + 1, 1e9);
// Parent array
vector<int> parent(n + 1);
/* Marking each node as
its own parent initially */
for (int i = 1; i <= n; i++)
parent[i] = i;
/* Distance of source node
(node 1) to itself is zero */
dist[1] = 0;
// Push the source node to the queue.
pq.push({0, 1});
// Until the queue is empty
while (!pq.empty())
{
/* Get the pair containing node having
minimum distance from source node */
auto it = pq.top();
pq.pop();
int node = it.second; // node
int dis = it.first; // distance
// Iterate through the neighbors
for (auto it : adj[node]) {
int adjNode = it.first; // node
int edWt = it.second; // edge weight
/* If the tentative distance to
reach adjacent node is smaller
than the known distance */
if (dis + edWt < dist[adjNode]) {
// Update the known distance
dist[adjNode] = dis + edWt;
// Push the new pair to priority queue
pq.push({dis + edWt, adjNode});
/* Update the parent of the adjNode
to the recent node(where it came from) */
parent[adjNode] = node;
}
}
}
/* If distance to the node could not be found,
return an array containing -1. */
if (dist[n] == 1e9)
return {-1};
// Array to store the path
vector<int> path;
// Start from the destination node
int node = n;
/* Iterate backwards from destination
to source through the parent array */
while (parent[node] != node) {
// Add the node to the path
path.push_back(node);
// Take a step back
node = parent[node];
}
// Add the source node to the path
path.push_back(1);
/* Since the path stored is in a
reverse order, reverse the array
to get the actual path */
reverse(path.begin(), path.end());
// Add the path weight in the beginning
path.insert(path.begin(), dist[n]);
// Return the result
return path;
}
};
int main() {
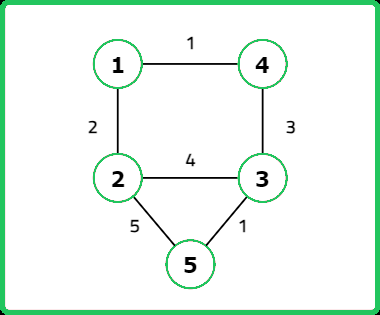
int n = 5, m = 6;
vector<vector<int>> edges = {
{1,2,2}, {2,5,5}, {2,3,4},
{1,4,1}, {4,3,3}, {3,5,1}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the shortest distance
of each node from the source node */
vector<int> ans = sol.shortestPath(n, m, edges);
// Output
cout << "The resulting path weight is: " << ans[0] << endl;
cout << "The path is: " << endl;
for(int i=1; i < ans.size(); i++) {
cout << ans[i] << " ";
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137
import java.util.*;
public class Solution {
/* Function to find the shortest
path from node 1 to node n */
public List<Integer> shortestPath(int n, int m, int[][] edges) {
// Adjacency list to store graph
List<List<int[]>> adj = new ArrayList<>();
for (int i = 0; i <= n; i++) {
adj.add(new ArrayList<>());
}
// Adding the edges to the graph
for (int[] edge : edges) {
adj.get(edge[0]).add(new int[]{edge[1], edge[2]});
adj.get(edge[1]).add(new int[]{edge[0], edge[2]});
}
/* Using priority queue to
implement Dijkstra Algorithm */
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
// Distance array
int[] dist = new int[n + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
// Parent array
int[] parent = new int[n + 1];
/* Marking each node as
its own parent initially */
for (int i = 1; i <= n; i++) {
parent[i] = i;
}
/* Distance of source node
(node 1) to itself is zero */
dist[1] = 0;
// Push the source node to the queue.
pq.add(new int[]{0, 1});
// Until the queue is empty
while (!pq.isEmpty()) {
/* Get the pair containing node having
minimum distance from source node */
int[] curr = pq.poll();
int node = curr[1]; // node
int dis = curr[0]; // distance
// Iterate through the neighbors
for (int[] neighbor : adj.get(node)) {
int adjNode = neighbor[0]; // node
int edWt = neighbor[1]; // edge weight
/* If the tentative distance to
reach adjacent node is smaller
than the known distance */
if (dis + edWt < dist[adjNode]) {
// Update the known distance
dist[adjNode] = dis + edWt;
// Push the new pair to priority queue
pq.add(new int[]{dis + edWt, adjNode});
/* Update the parent of the adjNode
to the recent node(where it came from) */
parent[adjNode] = node;
}
}
}
/* If distance to the node could not be found,
return an array containing -1. */
if (dist[n] == Integer.MAX_VALUE) {
return Arrays.asList(-1);
}
// Array to store the path
List<Integer> path = new ArrayList<>();
// Start from the destination node
int node = n;
/* Iterate backwards from destination
to source through the parent array */
while (parent[node] != node) {
// Add the node to the path
path.add(node);
// Take a step back
node = parent[node];
}
// Add the source node to the path
path.add(1);
/* Since the path stored is in a
reverse order, reverse the array
to get the actual path */
Collections.reverse(path);
// Add the path weight in the beginning
path.add(0, dist[n]);
// Return the result
return path;
}
public static void main(String[] args) {
int n = 5, m = 6;
int[][] edges = {
{1, 2, 2}, {2, 5, 5}, {2, 3, 4},
{1, 4, 1}, {4, 3, 3}, {3, 5, 1}
};
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to find the shortest distance
of each node from the source node */
List<Integer> ans = sol.shortestPath(n, m, edges);
// Output
System.out.println("The resulting path weight is: " + ans.get(0));
System.out.println("The path is: ");
for (int i = 1; i < ans.size(); i++) {
System.out.print(ans.get(i) + " ");
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110
import heapq
class Solution:
# Function to find the shortest
# path from node 1 to node n
def shortestPath(self, n, m, edges):
# Adjacency list to store graph
adj = [[] for _ in range(n + 1)]
# Adding the edges to the graph
for edge in edges:
adj[edge[0]].append((edge[1], edge[2]))
adj[edge[1]].append((edge[0], edge[2]))
# Using priority queue to
# implement Dijkstra Algorithm
pq = []
# Distance array
dist = [float('inf')] * (n + 1)
# Parent array
parent = list(range(n + 1))
# Distance of source node
# (node 1) to itself is zero
dist[1] = 0
# Push the source node to the queue.
heapq.heappush(pq, (0, 1))
# Until the queue is empty
while pq:
# Get the pair containing node having
# minimum distance from source node
dis, node = heapq.heappop(pq)
# Iterate through the neighbors
for adjNode, edWt in adj[node]:
# If the tentative distance to
# reach adjacent node is smaller
# than the known distance
if dis + edWt < dist[adjNode]:
# Update the known distance
dist[adjNode] = dis + edWt
# Push the new pair to priority queue
heapq.heappush(pq, (dis + edWt, adjNode))
# Update the parent of the adjNode
# to the recent node(where it came from)
parent[adjNode] = node
# If distance to the node could not be found,
# return an array containing -1.
if dist[n] == float('inf'):
return [-1]
# Array to store the path
path = []
# Start from the destination node
node = n
# Iterate backwards from destination
# to source through the parent array
while parent[node] != node:
# Add the node to the path
path.append(node)
# Take a step back
node = parent[node]
# Add the source node to the path
path.append(1)
# Since the path stored is in a
# reverse order, reverse the array
# to get the actual path
path.reverse()
# Add the path weight in the beginning
path.insert(0, dist[n])
# Return the result
return path
if __name__ == "__main__":
n = 5
m = 6
edges = [
[1, 2, 2], [2, 5, 5], [2, 3, 4],
[1, 4, 1], [4, 3, 3], [3, 5, 1]
]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to find the shortest distance
# of each node from the source node
ans = sol.shortestPath(n, m, edges)
# Output
print("The resulting path weight is:", ans[0])
print("The path is:")
for i in range(1, len(ans)):
print(ans[i], end=" ")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188
//Priority Queue Implementation
class MinPriorityQueue {
constructor() {
this.heap = [];
}
enqueue(element) {
this.heap.push(element);
this.bubbleUp();
}
dequeue() {
const min = this.heap[0];
const end = this.heap.pop();
if (this.heap.length > 0) {
this.heap[0] = end;
this.bubbleDown();
}
return min;
}
bubbleUp() {
let index = this.heap.length - 1;
const element = this.heap[index];
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2);
let parent = this.heap[parentIndex];
if (element[0] >= parent[0]) break;
this.heap[index] = parent;
index = parentIndex;
}
this.heap[index] = element;
}
bubbleDown() {
let index = 0;
const length = this.heap.length;
const element = this.heap[0];
while (true) {
let leftChildIndex = 2 * index + 1;
let rightChildIndex = 2 * index + 2;
let leftChild, rightChild;
let swap = null;
if (leftChildIndex < length) {
leftChild = this.heap[leftChildIndex];
if (leftChild[0] < element[0]) {
swap = leftChildIndex;
}
}
if (rightChildIndex < length) {
rightChild = this.heap[rightChildIndex];
if (
(swap === null && rightChild[0] < element[0]) ||
(swap !== null && rightChild[0] < leftChild[0])
) {
swap = rightChildIndex;
}
}
if (swap === null) break;
this.heap[index] = this.heap[swap];
index = swap;
}
this.heap[index] = element;
}
isEmpty() {
return this.heap.length === 0;
}
}
class Solution {
// Function to find the shortest
// path from node 1 to node n
shortestPath(n, m, edges) {
// Adjacency list to store graph
const adj = Array.from({ length: n + 1 }, () => []);
// Adding the edges to the graph
for (const edge of edges) {
adj[edge[0]].push([edge[1], edge[2]]);
adj[edge[1]].push([edge[0], edge[2]]);
}
// Using priority queue to
// implement Dijkstra Algorithm
const pq = new MinPriorityQueue();
// Distance array
const dist = new Array(n + 1).fill(Infinity);
// Parent array
const parent = Array.from({ length: n + 1 }, (_, i) => i);
// Distance of source node
// (node 1) to itself is zero
dist[1] = 0;
// Push the source node to the queue.
pq.enqueue([0, 1]);
// Until the queue is empty
while (!pq.isEmpty()) {
// Get the pair containing node having
// minimum distance from source node
const [dis, node] = pq.dequeue();
// Iterate through the neighbors
for (const [adjNode, edWt] of adj[node]) {
// If the tentative distance to
// reach adjacent node is smaller
// than the known distance
if (dis + edWt < dist[adjNode]) {
// Update the known distance
dist[adjNode] = dis + edWt;
// Push the new pair to priority queue
pq.enqueue([dis + edWt, adjNode]);
// Update the parent of the adjNode
// to the recent node(where it came from)
parent[adjNode] = node;
}
}
}
// If distance to the node could not be found,
// return an array containing -1.
if (dist[n] === Infinity) {
return [-1];
}
// Array to store the path
const path = [];
// Start from the destination node
let node = n;
// Iterate backwards from destination
// to source through the parent array
while (parent[node] !== node) {
// Add the node to the path
path.push(node);
// Take a step back
node = parent[node];
}
// Add the source node to the path
path.push(1);
// Since the path stored is in a
// reverse order, reverse the array
// to get the actual path
path.reverse();
// Add the path weight in the beginning
path.unshift(dist[n]);
// Return the result
return path;
}
}
const n = 5, m = 6;
const edges = [
[1,2,2], [2,5,5], [2,3,4],
[1,4,1], [4,3,3], [3,5,1]
];
// Creating an instance of
// Solution class
const sol = new Solution();
// Function call to find the shortest distance
// of each node from the source node
const ans = sol.shortestPath(n, m, edges);
// Output
console.log("The resulting path weight is:", ans[0]);
console.log("The path is:");
for (let i = 1; i < ans.length; i++) {
console.log(ans[i], " ");
}