Longest subarray with sum K

Intuition

To find the longest subarray with a sum of 𝑘, we'll check the sum of every possible subarray. We use two loops to pick all possible starting and ending indices, and another loop to calculate the sum of each subarray. If a subarray's sum is 𝑘, we compare its length to the longest one we've found so far. This way, we make sure to find the longest subarray with the sum of 𝑘.

Approach

First, we run a loop i to select every possible starting index of the subarray. These starting indices range from index 0 to n-1 (where n is the size of the array).
Inside this loop, we run another loop j to select the ending index of the subarray. For every subarray starting at index i, the ending index j can range from i to n-1.
Next, for each subarray starting from index i and ending at index j (i.e., arr[i...j]), we run an additional loop to calculate the sum of all the elements in that subarray.
If the sum equals k, we consider its length, which is (j-i+1). Among all such subarrays, we keep track of the maximum length by comparing all the lengths.

Dry Run: Please refer to the video for the dry-run.

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    int longestSubarray(vector<int> &nums, int k)
    {
        int n = nums.size(); 
        int maxLength = 0;

        // starting index
        for (int startIndex = 0; startIndex < n; startIndex++) { 
            // ending index
            for (int endIndex = startIndex; endIndex < n; endIndex++) { 
                /* add all the elements of 
                   subarray = nums[startIndex...endIndex]  */
                int currentSum = 0;
                for (int i = startIndex; i <= endIndex; i++) {
                    currentSum += nums[i];
                }

                if (currentSum == k)
                    maxLength = max(maxLength, endIndex - startIndex + 1);
            }
        }
        return maxLength;
    }
};

int main()
{
    vector<int> a = { -1, 1, 1 };
    int k = 1;

    // Create an instance of the Solution class
    Solution solution;
    // Function call to get the result
    int len = solution.longestSubarray(a, k);
    
    cout << "The length of the longest subarray is: " << len << "\n";
    return 0;
}

import java.util.*;

class Solution {
    public int longestSubarray(int[] nums, int k) {
        int n = nums.length; 
        int maxLength = 0;

        // starting index
        for (int startIndex = 0; startIndex < n; startIndex++) { 
            // ending index
            for (int endIndex = startIndex; endIndex < n; endIndex++) { 
                /* add all the elements of 
                   subarray = nums[startIndex...endIndex]  */
                int currentSum = 0;
                for (int i = startIndex; i <= endIndex; i++) {
                    currentSum += nums[i];
                }

                if (currentSum == k) {
                    maxLength = Math.max(maxLength, endIndex - startIndex + 1);
                }
            }
        }
        return maxLength;
    }

    public static void main(String[] args) {
        int[] nums = { -1, 1, 1 };
        int k = 1;

        // Create an instance of the Solution class
        Solution solution = new Solution();
        // Function call to get the result
        int len = solution.longestSubarray(nums, k);
        
        System.out.println("The length of the longest subarray is: " + len);
    }
}

class Solution:
    def longestSubarray(self, nums, k):
        n = len(nums) 
        maxLength = 0

        # starting index
        for startIndex in range(n):
            # ending index
            for endIndex in range(startIndex, n):
                # add all the elements of 
                # subarray = nums[startIndex...endIndex]
                currentSum = 0
                for i in range(startIndex, endIndex + 1):
                    currentSum += nums[i]

                if currentSum == k:
                    maxLength = max(maxLength, endIndex - startIndex + 1)

        return maxLength

if __name__ == "__main__":
    nums = [-1, 1, 1]
    k = 1

    # Create an instance of the Solution class
    solution = Solution()
    # Function call to get the result
    length = solution.longestSubarray(nums, k)
    
    print("The length of the longest subarray is:", length)

class Solution {
    longestSubarray(nums, k) {
        const n = nums.length;
        let maxLength = 0;

        // starting index
        for (let startIndex = 0; startIndex < n; startIndex++) {
            // ending index
            for (let endIndex = startIndex; endIndex < n; endIndex++) {
                /* add all the elements of 
                   subarray = nums[startIndex...endIndex] */
                let currentSum = 0;
                for (let i = startIndex; i <= endIndex; i++) {
                    currentSum += nums[i];
                }

                if (currentSum === k) {
                    maxLength = Math.max(maxLength, endIndex - startIndex + 1);
                }
            }
        }
        return maxLength;
    }
}

const nums = [-1, 1, 1];
const k = 1;

// Create an instance of the Solution class
const solution = new Solution();
// Function call to get the result
const length = solution.longestSubarray(nums, k);

console.log("The length of the longest subarray is:", length);

Complexity Analysis

Time Complexity: O(N³), where N is the size of the array. Since we are using three nested loops, each running approximately N times.

Space Complexity: O(1), as we are not using any extra space.

Intuition

In this approach, we use the concept of prefix sums to solve the problem of finding the longest subarray with a sum equal to 𝑘. The prefix sum of a subarray ending at index 𝑖 is simply the sum of all the elements of that subarray. By keeping track of these prefix sums and their occurrences, we can efficiently determine the longest subarray that meets the criteria.

Approach

First, we will declare a map to store the prefix sums and their corresponding indices.
We will run a loop from index 0 to n-1 (where n is the size of the array).
For each index i, add the current element a[i] to the prefix sum. If the prefix sum equals k, consider the length of the current subarray (i+1) and update the maximum length if needed. Calculate the prefix sum for the remaining subarray (prefix sum - k).
If this remaining sum exists in the map, calculate the length of the subarray ending at i and starting after the prefix sum, i.e., i - map[remaining sum], and update the maximum length if this length is greater. If the remaining sum does not exist in the map, add the current prefix sum and index to the map to ensure we store the earliest index where each prefix sum occurs.
The prefix sum of a subarray ending at index i is simply the sum of all the elements up to that index. By tracking these sums and their occurrences, we can efficiently determine the longest subarray that sums to k.

Observations

Assume the prefix sum of a subarray ending at index i is x. We need to find another subarray ending at i whose sum equals k. If such a subarray exists, the prefix sum of the remaining part will be x-k.

For a subarray ending at index i with the prefix sum x, if we remove the part with the prefix sum x-k, we are left with a subarray whose sum equals k. This is our target.

Instead of searching for subarrays with sum k, we will use a map to track the prefix sums at each index. The map will store each prefix sum and its corresponding index as a key-value pair. At index i, we will check the map for the prefix sum x-k. If it exists, we calculate the subarray length as i - preSumMap[x-k]. We update the maximum length if this subarray is longer.

We repeat this process for all indices from 0 to n-1 (where n is the size of the array).

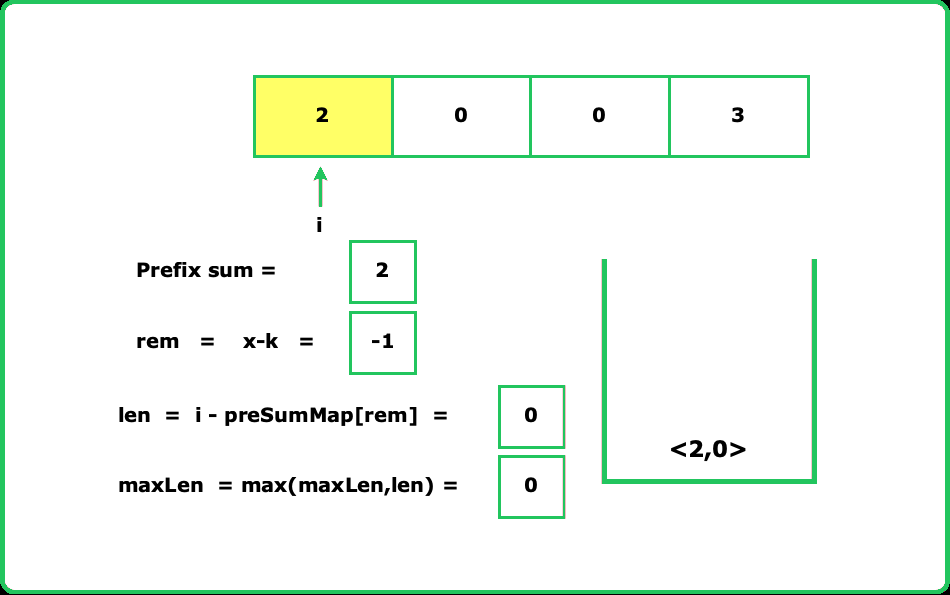
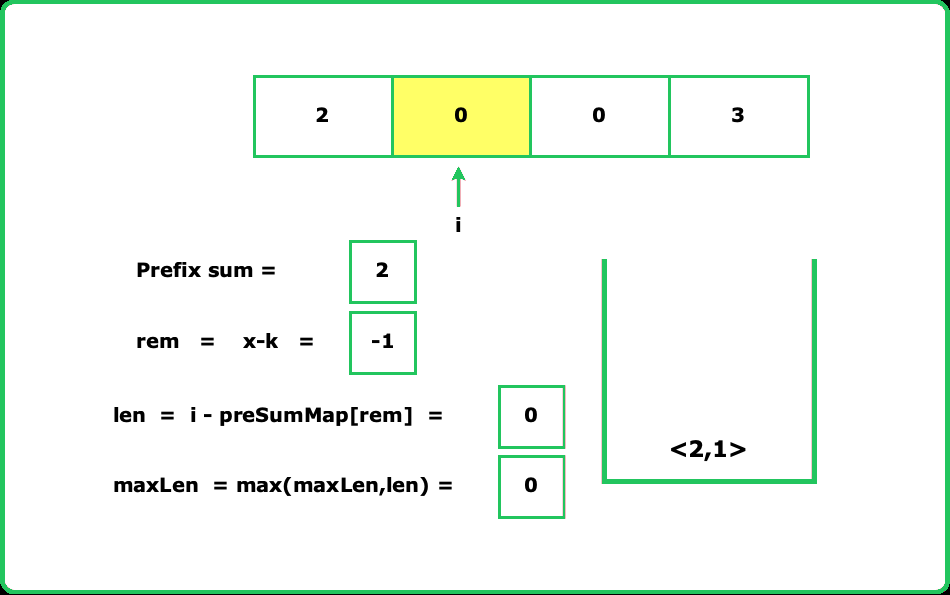
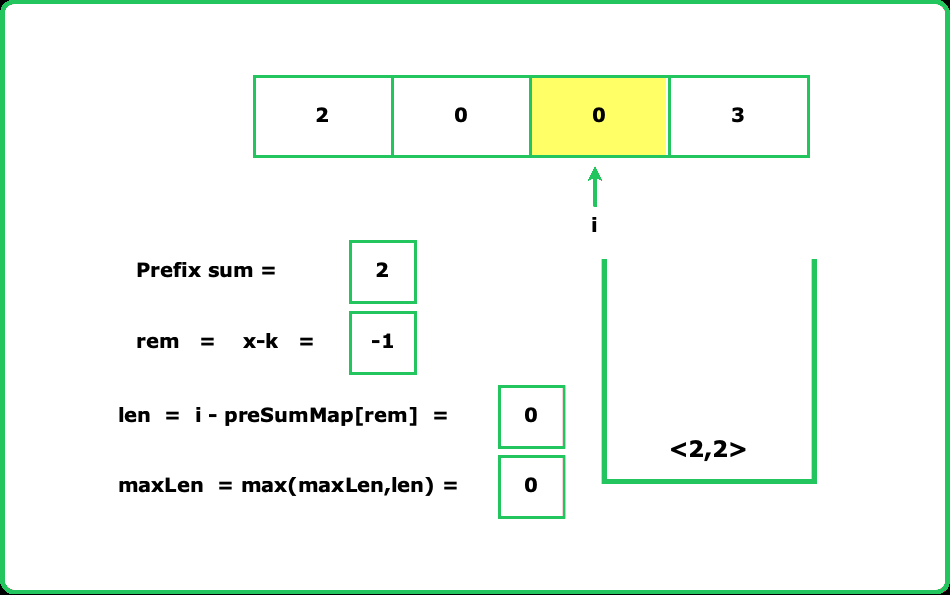
Edge Case

Why do we need to check if the prefix sum already exists in the map? Let's understand with an example:

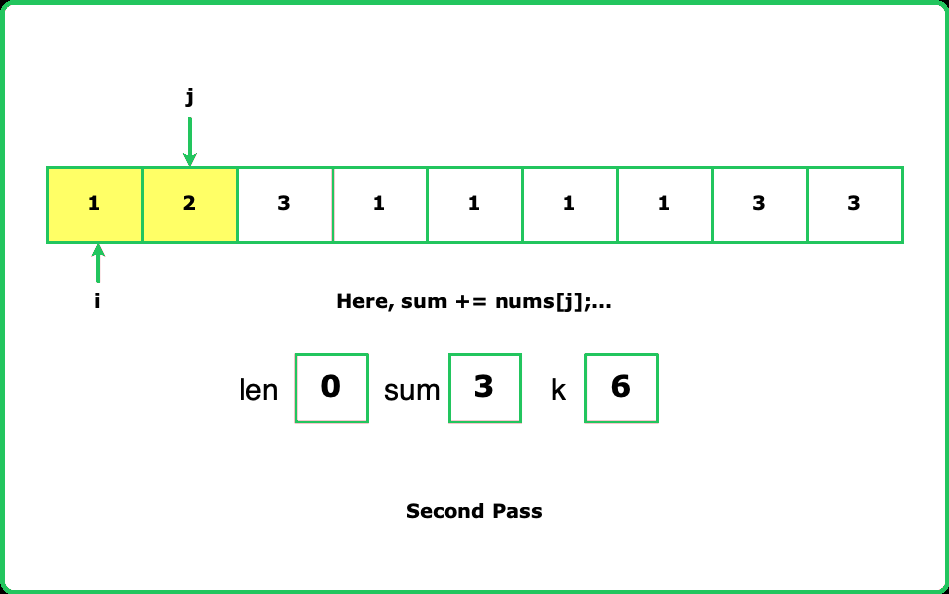
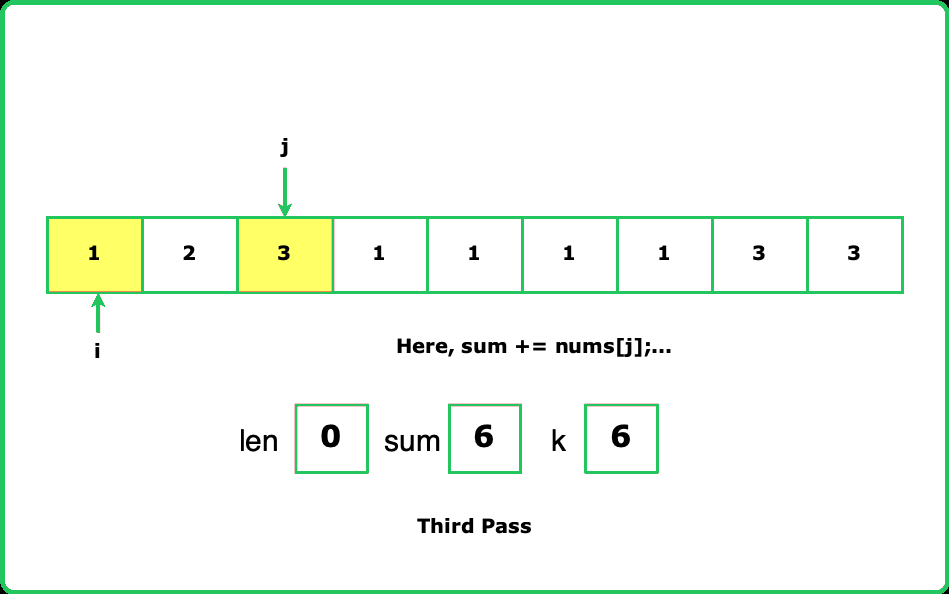
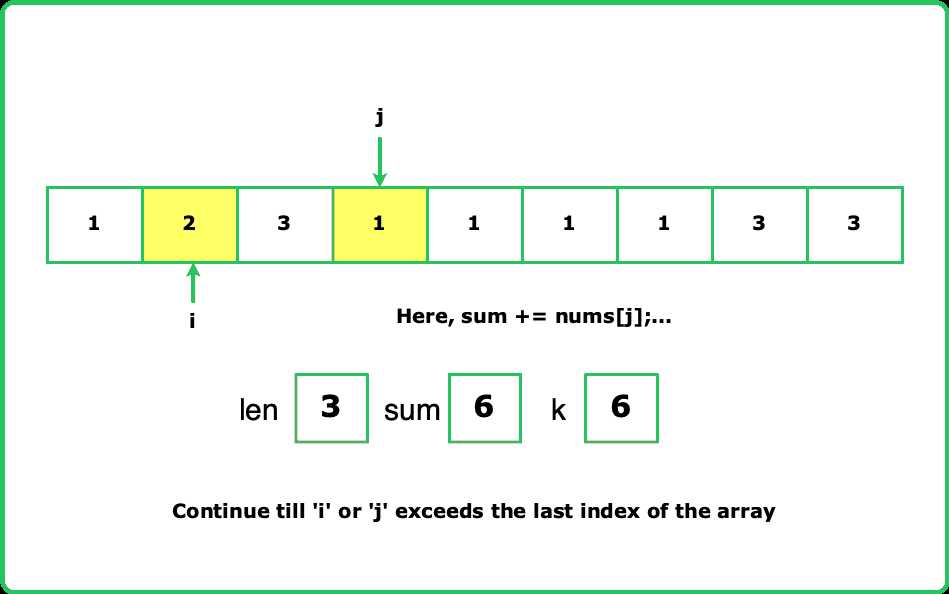
Assume the array is [2, 0, 0, 3]. If we don't check the map before inserting, the algorithm might incorrectly update the index for repeated prefix sums. For instance, at indices 2 and 3, the prefix sum remains the same but the index is updated. When i reaches the end, the calculated length might be incorrect. To avoid this, we only update the map with the first occurrence of each prefix sum. This ensures we get the maximum subarray length. Take the reference of the below image for better understanding.

Dry Run

Please refer to the video for the dry-run.

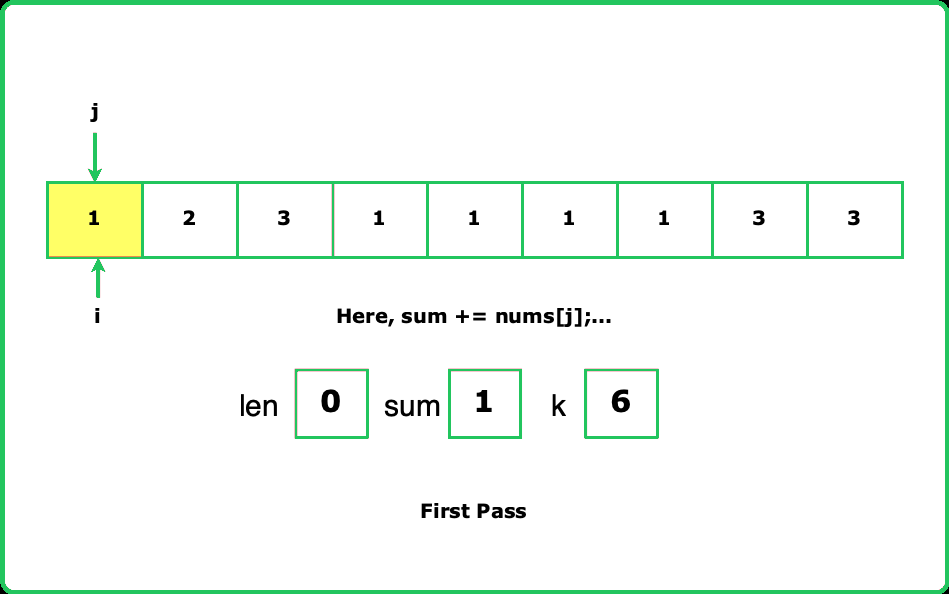
#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    int longestSubarray(vector<int> &nums, int k)
    {
        int n = nums.size(); 

        map<int, int> preSumMap;
        int sum = 0;
        int maxLen = 0;
        for (int i = 0; i < n; i++) {
            // calculate the prefix sum till index i
            sum += nums[i];

            // if the sum equals k, update maxLen
            if (sum == k) {
                maxLen = max(maxLen, i + 1);
            }

            // calculate the sum of remaining part i.e., sum - k
            int rem = sum - k;

            // calculate the length and update maxLen
            if (preSumMap.find(rem) != preSumMap.end()) {
                int len = i - preSumMap[rem];
                maxLen = max(maxLen, len);
            }

            // update the map if sum is not already present
            if (preSumMap.find(sum) == preSumMap.end()) {
                preSumMap[sum] = i;
            }
        }

        return maxLen;
    }
};

int main()
{
    vector<int> a = { -1, 1, 1 };
    int k = 1;

    // Create an instance of the Solution class
    Solution solution;
    // Function call to get the result
    int len = solution.longestSubarray(a, k);
   
    cout << "The length of the longest subarray is: " << len << "\n";
    return 0;
}

import java.util.*;

class Solution {
    public int longestSubarray(int[] nums, int k) {
        int n = nums.length;

        Map<Integer, Integer> preSumMap = new HashMap<>();
        int sum = 0;
        int maxLen = 0;
        for (int i = 0; i < n; i++) {
            // calculate the prefix sum till index i
            sum += nums[i];

            // if the sum equals k, update maxLen
            if (sum == k) {
                maxLen = Math.max(maxLen, i + 1);
            }

            // calculate the sum of remaining part i.e., sum - k
            int rem = sum - k;

            // calculate the length and update maxLen
            if (preSumMap.containsKey(rem)) {
                int len = i - preSumMap.get(rem);
                maxLen = Math.max(maxLen, len);
            }

            // update the map if sum is not already present
            if (!preSumMap.containsKey(sum)) {
                preSumMap.put(sum, i);
            }
        }

        return maxLen;
    }

    public static void main(String[] args) {
        int[] nums = { -1, 1, 1 };
        int k = 1;

        // Create an instance of the Solution class
        Solution solution = new Solution();
        // Function call to get the result
        int len = solution.longestSubarray(nums, k);
        
        System.out.println("The length of the longest subarray is: " + len);
    }
}

class Solution:
    def longestSubarray(self, nums, k):
        n = len(nums)  

        preSumMap = {}
        sum = 0
        maxLen = 0
        for i in range(n):
            # calculate the prefix sum till index i
            sum += nums[i]

            # if the sum equals k, update maxLen
            if sum == k:
                maxLen = max(maxLen, i + 1)

            # calculate the sum of remaining part i.e., sum - k
            rem = sum - k

            # calculate the length and update maxLen
            if rem in preSumMap:
                length = i - preSumMap[rem]
                maxLen = max(maxLen, length)

            # update the map if sum is not already present
            if sum not in preSumMap:
                preSumMap[sum] = i

        return maxLen

if __name__ == "__main__":
    nums = [-1, 1, 1]
    k = 1

    # Create an instance of the Solution class
    solution = Solution()
    # Function call to get the result
    length = solution.longestSubarray(nums, k)
    
    print("The length of the longest subarray is:", length)

class Solution {
    longestSubarray(nums, k) {
        const n = nums.length;

        const preSumMap = new Map();
        let sum = 0;
        let maxLen = 0;
        for (let i = 0; i < n; i++) {
            // calculate the prefix sum till index i
            sum += nums[i];

            // if the sum equals k, update maxLen
            if (sum === k) {
                maxLen = Math.max(maxLen, i + 1);
            }

            // calculate the sum of remaining part i.e., sum - k
            const rem = sum - k;

            // calculate the length and update maxLen
            if (preSumMap.has(rem)) {
                const len = i - preSumMap.get(rem);
                maxLen = Math.max(maxLen, len);
            }

            // update the map if sum is not already present
            if (!preSumMap.has(sum)) {
                preSumMap.set(sum, i);
            }
        }

        return maxLen;
    }
}

const nums = [-1, 1, 1];
const k = 1;

// Create an instance of the Solution class
const solution = new Solution();
// Function call to get the result
const len = solution.longestSubarray(nums, k);

console.log("The length of the longest subarray is:", len);

Complexity Analysis

Time Complexity: O(N) or O(NxlogN) depending on the map data structure used, where N is the size of the array. For example, using an unordered_map in C++ gives a time complexity of O(N) (though in the worst case, unordered_map takes O(N) to find an element, making the time complexity O(N²)). If we use a map data structure, the time complexity is O(NxlogN). The best case complexity is O(N) as we are traversing the array with a loop.

Space Complexity: O(N), since we are using a map data structure.

Note that this approach is Only valid for positive numbers. As per the question, the elements in the array can be negative as well. This means submitting this code in the editorial will give you a wrong submission.

Intuition:

The idea is to solve the problem in linear time without using extra space. Since, we are only considered about the subarray, we can use two pointers and sliding window concept to find the required subarray. Assuming that all the elements in the array are psoitive we can form a window representing the subarray with the following observations:

To increase the sum of the elements in window, we can expand the window by one element.
To decrease the sum of the elements in window, we can shrink the window by one element.

This is only possible if the elements in the array are positives. Because of these observations, we will be able to find the longest subarray with sum K provided all the elements in the array are positive.

Approach:

Two pointers (left and right) are used to maintain the current window of elements in the array.
A variable (sum) keeps track of the sum of the elements in the current window.
The right pointer expands the window by including new elements.
If the sum of the window exceeds k, the left pointer shrinks the window by removing elements from the start until the sum is less than or equal to k.
If the sum of the current window equals k, the maximum length of such a subarray is updated.
The process continues until the right pointer traverses the entire array.
The maximum length of the subarray with sum k is returned as the result.

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    // Function to find the length of longest subarray having sum k
    int longestSubarray(vector<int> &nums, int k){
        int n = nums.size();
        
        // To store the maximum length of the subarray
        int maxLen = 0;
        
        // Pointers to mark the start and end of window
        int left = 0, right = 0;
        
        // To store the sum of elements in the window
        int sum = nums[0];
        
        // Traverse all the elements
        while(right < n) {
            
            // If the sum exceeds K, shrink the window
            while(left <= right && sum > k) {
                sum -= nums[left];
                left++;
            }
            
            // store the maximum length
            if(sum == k) {
                maxLen = max(maxLen, right - left + 1);
            }
            
            right++;
            if(right < n) sum += nums[right];
        }
        
        return maxLen;
    }
};

int main() {
	vector<int> nums = {10, 5, 2, 7, 1, 9};
    int k = 15;
    
	// Creating an object of Solution class
	Solution sol;

	/* Function call to find the length
	of longest subarray having sum k */
	int ans = sol.longestSubarray(nums, k);

	cout << "The length of longest subarray having sum k is: " << ans;

	return 0;
}
import java.util.*;

class Solution {
    public int longestSubarray(int[] nums, int k) {
        int n = nums.length;

        // To store the maximum length of the subarray
        int maxLen = 0;

        // Pointers to mark the start and end of window
        int left = 0, right = 0;

        // To store the sum of elements in the window
        int sum = nums[0];

        // Traverse all the elements
        while (right < n) {

            // If the sum exceeds K, shrink the window
            while (left <= right && sum > k) {
                sum -= nums[left];
                left++;
            }

            // Store the maximum length
            if (sum == k) {
                maxLen = Math.max(maxLen, right - left + 1);
            }

            right++;
            if (right < n) sum += nums[right];
        }

        return maxLen;
    }
}

class Main {
    public static void main(String[] args) {
        int[] nums = {10, 5, 2, 7, 1, 9};
        int k = 15;

        // Creating an object of Solution class
        Solution sol = new Solution();

        /* Function call to find the length
        of longest subarray having sum k */
        int ans = sol.longestSubarray(nums, k);

        System.out.println("The length of longest subarray having sum k is: " + ans);
    }
}
class Solution:
    # Function to find the length of longest subarray having sum k
    def longestSubarray(self, nums, k):
        n = len(nums)
        
        # To store the maximum length of the subarray
        maxLen = 0
        
        # Pointers to mark the start and end of window
        left = 0
        right = 0
        
        # To store the sum of elements in the window
        sum = nums[0]
        
        # Traverse all the elements
        while right < n:
            
            # If the sum exceeds K, shrink the window
            while left <= right and sum > k:
                sum -= nums[left]
                left += 1
            
            # Store the maximum length
            if sum == k:
                maxLen = max(maxLen, right - left + 1)
            
            right += 1
            if right < n:
                sum += nums[right]
        
        return maxLen


nums = [10, 5, 2, 7, 1, 9]
k = 15

# Creating an object of Solution class
sol = Solution()

# Function call to find the length
# of longest subarray having sum k
ans = sol.longestSubarray(nums, k)

print(f"The length of longest subarray having sum k is: {ans}")
class Solution {
    // Function to find the length of longest subarray having sum k
    longestSubarray(nums, k) {
        let n = nums.length;
        
        // To store the maximum length of the subarray
        let maxLen = 0;
        
        // Pointers to mark the start and end of window
        let left = 0, right = 0;
        
        // To store the sum of elements in the window
        let sum = nums[0];
        
        // Traverse all the elements
        while (right < n) {
            
            // If the sum exceeds K, shrink the window
            while (left <= right && sum > k) {
                sum -= nums[left];
                left++;
            }
            
            // Store the maximum length
            if (sum === k) {
                maxLen = Math.max(maxLen, right - left + 1);
            }
            
            right++;
            if (right < n) sum += nums[right];
        }
        
        return maxLen;
    }
}

// Input array and target sum
const nums = [10, 5, 2, 7, 1, 9];
const k = 15;

// Creating an object of Solution class
const sol = new Solution();

/* Function call to find the length
of longest subarray having sum k */
const ans = sol.longestSubarray(nums, k);

console.log(`The length of longest subarray having sum k is: ${ans}`);

Complexity Analysis:

Time Complexity: O(N), where N is the size of the array.
There are two pointers left and right which traverse the array at once taking linear time.

Space Complexity: O(1), as only a couple of variables are used.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Approach

Complexity Analysis

Intuition

Approach

Dry Run

Complexity Analysis

Intuition:

Approach:

Solution:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code