Median of 2 sorted arrays

Intuition:

The extremely naive approach is to merge the two sorted arrays and then find the median of the final merged array. Given that the arrays are already sorted, the merge approach of the merge sort algorithm can be used. This approach iterates through both arrays, picking the smallest elements first and then the larger ones, resulting in a final sorted array.

Approach:

If the length of the merged array is even: The median is the average of the two middle elements. The index = (sizeOfMergedArray) / 2, median will be the sum of element at 'index' and the element at 'index-1' divided by 2.
If the length of the merged array is odd: index = (sizeOfMergedArray) / 2, median will be the element at 'index'
Initialize an array of size equal to sum of size of 1st array and size of 2nd array to store the elements of the merged array.
Now, take two pointers i and j, where i points to the first element of arr1 and j points to the first element of arr2.
Next, initialize a while loop, which will run till any one of the pointers crosses the size of their respective array. If the element at pointer i is less than or equal to element at pointer j, then insert the element at pointer i in the merged array and increase i by 1. Otherwise, insert the element at j into the merged array and increase j by 1.
After that, the left-out elements from both arrays will be copied as it is into the merged array. Now, the merged array will be sorted, find the mediun based on the size of the array if it is even or odd. Finally, return the value of the median.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find the median of two sorted arrays.
    double median(vector<int>& arr1, vector<int>& arr2) {
        // Size of two given arrays
        int n1 = arr1.size(), n2 = arr2.size();

        vector<int> merged;
        // Apply the merge step
        int i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) merged.push_back(arr1[i++]);
            else merged.push_back(arr2[j++]);
        }

        // Copy the remaining elements
        while (i < n1) merged.push_back(arr1[i++]);
        while (j < n2) merged.push_back(arr2[j++]);

        // Find the median
        int n = n1 + n2;
        if (n % 2 == 1) {
            return (double)merged[n / 2];
        }

        double median = ((double)merged[n / 2] + (double)merged[(n / 2) - 1]) / 2.0;
        return median;
    }
};

int main() {
    vector<int> a = {1, 4, 7, 10, 12};
    vector<int> b = {2, 3, 6, 15};

    // Create an instance of the Solution class
    Solution sol;

    // Print the median of the two sorted arrays
    cout << "The median of two sorted arrays is " << fixed << setprecision(1)
         << sol.median(a, b) << '\n';

    return 0;
}
import java.util.*;

class Solution {
    //Function to find the median of two sorted arrays.
    public double median(int[] arr1, int[] arr2) {
        // Size of two given arrays
        int n1 = arr1.length, n2 = arr2.length;

        int[] merged = new int[n1 + n2];
        // Apply the merge step
        int i = 0, j = 0, k = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) merged[k++] = arr1[i++];
            else merged[k++] = arr2[j++];
        }

        // Copy the remaining elements
        while (i < n1) merged[k++] = arr1[i++];
        while (j < n2) merged[k++] = arr2[j++];

        // Find the median
        int n = n1 + n2;
        if (n % 2 == 1) {
            return (double) merged[n / 2];
        }

        double median = ((double) merged[n / 2] + (double) merged[(n / 2) - 1]) / 2.0;
        return median;
    }

    public static void main(String[] args) {
        int[] a = {1, 4, 7, 10, 12};
        int[] b = {2, 3, 6, 15};

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Print the median of the two sorted arrays
        System.out.println("The median of two sorted arrays is " + sol.median(a, b));
    }
}
class Solution:
    #Function to find the median of two sorted arrays.
    def median(self, arr1, arr2):
        # Size of two given arrays
        n1, n2 = len(arr1), len(arr2)

        merged = []
        # Apply the merge step
        i, j = 0, 0
        while i < n1 and j < n2:
            if arr1[i] < arr2[j]:
                merged.append(arr1[i])
                i += 1
            else:
                merged.append(arr2[j])
                j += 1

        # Copy the remaining elements
        while i < n1:
            merged.append(arr1[i])
            i += 1
        while j < n2:
            merged.append(arr2[j])
            j += 1

        # Find the median
        n = n1 + n2
        if n % 2 == 1:
            return float(merged[n // 2])

        median = (float(merged[n // 2]) + float(merged[(n // 2) - 1])) / 2.0
        return median

if __name__ == "__main__":
    a = [1, 4, 7, 10, 12]
    b = [2, 3, 6, 15]
    
    # Create an instance of the Solution class
    sol = Solution()
    
    # Print the median of the two sorted arrays
    print("The median of two sorted arrays is", sol.median(a, b))
class Solution {
    //Function to find the median of two sorted arrays.
    median(arr1, arr2) {
        // Size of two given arrays
        let n1 = arr1.length, n2 = arr2.length;

        let merged = [];
        // Apply the merge step
        let i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) merged.push(arr1[i++]);
            else merged.push(arr2[j++]);
        }

        // Copy the remaining elements
        while (i < n1) merged.push(arr1[i++]);
        while (j < n2) merged.push(arr2[j++]);

        // Find the median
        let n = n1 + n2;
        if (n % 2 === 1) {
            return merged[Math.floor(n / 2)];
        }

        let median = (merged[n / 2] + merged[(n / 2) - 1]) / 2.0;
        return median;
    }
}

const a = [1, 4, 7, 10, 12];
const b = [2, 3, 6, 15];

//Create an instance of Solution class
const sol = new Solution();

// Print the answer
console.log("The answer is:", sol.median(a, b));

Complexity Analysis:

Time Complexity:O(N1+N2), where N1 and N2 are the sizes of the given arrays. As, both are arrays are being traversed linearly.

Space Complexity:O(N1+N2), As, an extra array of size (N1+N2) is being used to solve this problem.

Intuition:

The idea here is to optimize the extra space used in the brute-force approach by eliminating the array used to store the final merged result. Upon closer observation, it can be noticed that only the two middle elements at indices [(sum of the sizes of both arrays) / 2] and [((sum of the sizes of both arrays) / 2) - 1] are needed, rather than the entire merged array, to effectively solve the problem. Stick to the same basic approach, but instead of storing elements in a separate array, use a counter called cnt to represent the imaginary third array's index. While traversing through the arrays, when 'cnt' reaches either index (sum of size of both the arrays)/2 or ((sum of size of both the arrays)/2)-1, store that particular element. This way, the same goal can be achieved without using any extra space.

Approach:

Initaialize the two indices as ind2 = (n1+n2)/2 and ind1 = ((n1+n2)/2)-1. These indices are showing the position of medians in the merged array. Also, declare the counter called ‘cnt’ and initialize it with 0.
Now, take two pointers i and j, where i points to the first element of arr1 and j points to the first element of arr2.
Next, initialize a while loop, which will run till any one of the pointers crosses the size of their respective array. If the element at pointer i is less than or equal to element at pointer j, then check if 'cnt' is equal to any of the indices of the medians, if so, store the element at index i. Then increase i and 'cnt' by 1. Otherwise, check if 'cnt' is equal to any of the indices of the medians, if so, store the element at index j. Then increase j and 'cnt' by 1.
After that, traverse the left-out elements from both arrays and perform the above step.
If the total length i.e. (sum of size of both the arrays) is even, then median is the average of the elements at ind1 and ind2. Else, median will be the element at indexind2

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find the median of two sorted arrays.
    double median(vector<int>& arr1, vector<int>& arr2) {
        // Size of two given arrays
        int n1 = arr1.size(), n2 = arr2.size();
        int n = n1 + n2; // Total size

        // Required indices for median calculation
        int ind2 = n / 2;
        int ind1 = ind2 - 1;
        int cnt = 0;
        int ind1el = -1, ind2el = -1;

        // Apply the merge step
        int i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) {
                if (cnt == ind1) ind1el = arr1[i];
                if (cnt == ind2) ind2el = arr1[i];
                cnt++;
                i++;
            } else {
                if (cnt == ind1) ind1el = arr2[j];
                if (cnt == ind2) ind2el = arr2[j];
                cnt++;
                j++;
            }
        }

        // Copy the remaining elements
        while (i < n1) {
            if (cnt == ind1) ind1el = arr1[i];
            if (cnt == ind2) ind2el = arr1[i];
            cnt++;
            i++;
        }
        while (j < n2) {
            if (cnt == ind1) ind1el = arr2[j];
            if (cnt == ind2) ind2el = arr2[j];
            cnt++;
            j++;
        }

        // Find the median
        if (n % 2 == 1) {
            return (double) ind2el;
        }

        return (double) ((double) (ind1el + ind2el)) / 2.0;
    }
};

int main() {
    vector<int> a = {1, 4, 7, 10, 12};
    vector<int> b = {2, 3, 6, 15};

    // Create an instance of the Solution class
    Solution sol;

    // Print the median of the two sorted arrays
    cout << "The median of two sorted arrays is " << fixed << setprecision(1)
         << sol.median(a, b) << '\n';

    return 0;
}
import java.util.Arrays;

class Solution {
    //Function to find the median of two sorted arrays.
    public double median(int[] arr1, int[] arr2) {
        // Size of two given arrays
        int n1 = arr1.length, n2 = arr2.length;
        int n = n1 + n2; // Total size

        // Required indices for median calculation
        int ind2 = n / 2;
        int ind1 = ind2 - 1;
        int cnt = 0;
        int ind1el = -1, ind2el = -1;

        // Apply the merge step
        int i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) {
                if (cnt == ind1) ind1el = arr1[i];
                if (cnt == ind2) ind2el = arr1[i];
                cnt++;
                i++;
            } else {
                if (cnt == ind1) ind1el = arr2[j];
                if (cnt == ind2) ind2el = arr2[j];
                cnt++;
                j++;
            }
        }

        // Copy the remaining elements
        while (i < n1) {
            if (cnt == ind1) ind1el = arr1[i];
            if (cnt == ind2) ind2el = arr1[i];
            cnt++;
            i++;
        }
        while (j < n2) {
            if (cnt == ind1) ind1el = arr2[j];
            if (cnt == ind2) ind2el = arr2[j];
            cnt++;
            j++;
        }

        // Find the median
        if (n % 2 == 1) {
            return (double) ind2el;
        }

        return (double) ((double) (ind1el + ind2el)) / 2.0;
    }

    public static void main(String[] args) {
        int[] a = {1, 4, 7, 10, 12};
        int[] b = {2, 3, 6, 15};

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Print the median of the two sorted arrays
        System.out.printf("The median of two sorted arrays is %.1f\n", sol.median(a, b));
    }
}
class Solution:
    #Function to find the median of two sorted arrays.
    def median(self, arr1, arr2):
        # Size of two given arrays
        n1, n2 = len(arr1), len(arr2)
        n = n1 + n2  # Total size

        # Required indices for median calculation
        ind2 = n // 2
        ind1 = ind2 - 1
        cnt = 0
        ind1el, ind2el = -1, -1

        # Apply the merge step
        i, j = 0, 0
        while i < n1 and j < n2:
            if arr1[i] < arr2[j]:
                if cnt == ind1:
                    ind1el = arr1[i]
                if cnt == ind2:
                    ind2el = arr1[i]
                cnt += 1
                i += 1
            else:
                if cnt == ind1:
                    ind1el = arr2[j]
                if cnt == ind2:
                    ind2el = arr2[j]
                cnt += 1
                j += 1

        # Copy the remaining elements
        while i < n1:
            if cnt == ind1:
                ind1el = arr1[i]
            if cnt == ind2:
                ind2el = arr1[i]
            cnt += 1
            i += 1
        while j < n2:
            if cnt == ind1:
                ind1el = arr2[j]
            if cnt == ind2:
                ind2el = arr2[j]
            cnt += 1
            j += 1

        # Find the median
        if n % 2 == 1:
            return float(ind2el)

        return float((ind1el + ind2el) / 2)

if __name__ == "__main__":
    a = [1, 4, 7, 10, 12]
    b = [2, 3, 6, 15]

    # Create an instance of the Solution class
    sol = Solution()

    # Print the median of the two sorted arrays
    print(f"The median of two sorted arrays is {sol.median(a, b)}")
class Solution {
     //Function to find the median of two sorted arrays.
    median(arr1, arr2) {
        // Size of two given arrays
        const n1 = arr1.length, n2 = arr2.length;
        const n = n1 + n2; // Total size

        // Required indices for median calculation
        const ind2 = Math.floor(n / 2);
        const ind1 = ind2 - 1;
        let cnt = 0;
        let ind1el = -1, ind2el = -1;

        // Apply the merge step
        let i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) {
                if (cnt === ind1) ind1el = arr1[i];
                if (cnt === ind2) ind2el = arr1[i];
                cnt++;
                i++;
            } else {
                if (cnt === ind1) ind1el = arr2[j];
                if (cnt === ind2) ind2el = arr2[j];
                cnt++;
                j++;
            }
        }

        // Copy the remaining elements
        while (i < n1) {
            if (cnt === ind1) ind1el = arr1[i];
            if (cnt === ind2) ind2el = arr1[i];
            cnt++;
            i++;
        }
        while (j < n2) {
            if (cnt === ind1) ind1el = arr2[j];
            if (cnt === ind2) ind2el = arr2[j];
            cnt++;
            j++;
        }

        // Find the median
        if (n % 2 === 1) {
            return ind2el;
        }

        return (ind1el + ind2el) / 2;
    }
}

const a = [1, 4, 7, 10, 12];
const b = [2, 3, 6, 15];

// Create an instance of the Solution class
const sol = new Solution();

// Print the median of the two sorted arrays
console.log(`The median of two sorted arrays is ${sol.median(a, b)}`);

Complexity Analysis:

Time Complexity:O(N1+N2), where N1 and N2 are the sizes of the given arrays. As, both are arrays are being traversed linearly.

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Intuition:

Here, the idea is to use the Binary Search algorithm to optimize the approach. The primary objective of Binary Search is to efficiently determine the appropriate half to eliminate, thereby reducing the search space by half. It achieves this by identifying a specific condition that ensures the target is not present in that half. Now, let’s observe how to apply binary search in this problem. First, we'll solve the problem where the sum of the sizes of both arrays is even; we'll consider the odd case later.

Observation: Assume, n = sum of size of both the arrays. Characteristics of each half is that it contains (n/2) elements. Each half contains x elements from the first array and [(n/2)-x] elements from the second array. The value of x might be different for the two halves. The unique configuration of halves: Considering different values of x, one can get different left and right halves(x = the number of elements taken from the first array for a particular half). Some different configurations for the above example are shown below: Median creates a partition on the final merged array: Upon closer observation, we can easily show that the median divides the final merged array into two halves. For example, How to solve the problem using the above observations:

For a valid merged array, the configurations of the two halves are unique. So, we can try to form the halves with different values of x, where x = the number of elements taken from arr1[] for a particular half.
There's no need to construct both halves. Once we have the correct left half, the right half is automatically determined, consisting of the remaining elements not yet considered. Therefore, our focus will solely be on creating the unique left half.
How to form all configurations of the left half: We know that the left half will surely contain x elements from arr1[] and (n/2)-x elements from arr2[]. Here the only variable is x. The minimum possible value of x is 0 and the maximum possible value is n1(i.e. The length of the considered array).
For all the values,[0, n1] of x, we will try to form the left half and then we will check if that half’s configuration is valid.

Check if the formed left half is valid:

For a valid left half, the merged array will always be sorted. So, if the merged array containing the formed left half is sorted, the formation is valid. How to check if the merged array is sorted without forming the array: In order to check we will consider 4 elements, i.e. l1, l2, r1, r2.
l1 = the maximum element belonging to arr1[] of the left half.
l2 = the maximum element belonging to arr2[] of the left half.
r1 = the minimum element belonging to arr1[] of the right half.
r1 = the minimum element belonging to arr2[] of the right half.

How to apply binary search to form the left half:

We will check the formation of the left half for all possible values of x. Now, we know that the minimum possible value of x is 0 and the maximum is n1(i.e. The length of the considered array). Now the range is sorted. So, we will apply the binary search on the possible values of x i.e. [0, n1].

How to eliminate the halves based on the values of x:

Binary search works by eliminating the halves in each step. Upon closer observation, we can eliminate the halves based on the following conditions:
If l1 > r2: This implies that we have considered more elements from arr1[] than necessary. So, we have to take less elements from arr1[] and more from arr2[]. In such a scenario, we should try smaller values of x. To achieve this, we will eliminate the right half (high = mid-1).
If l2 > r1: This implies that we have considered more elements from arr2[] than necessary. So, we have to take less elements from arr2[] and more from arr1[]. In such a scenario, we should try bigger values of x. To achieve this, we will eliminate the left half (low = mid+1).

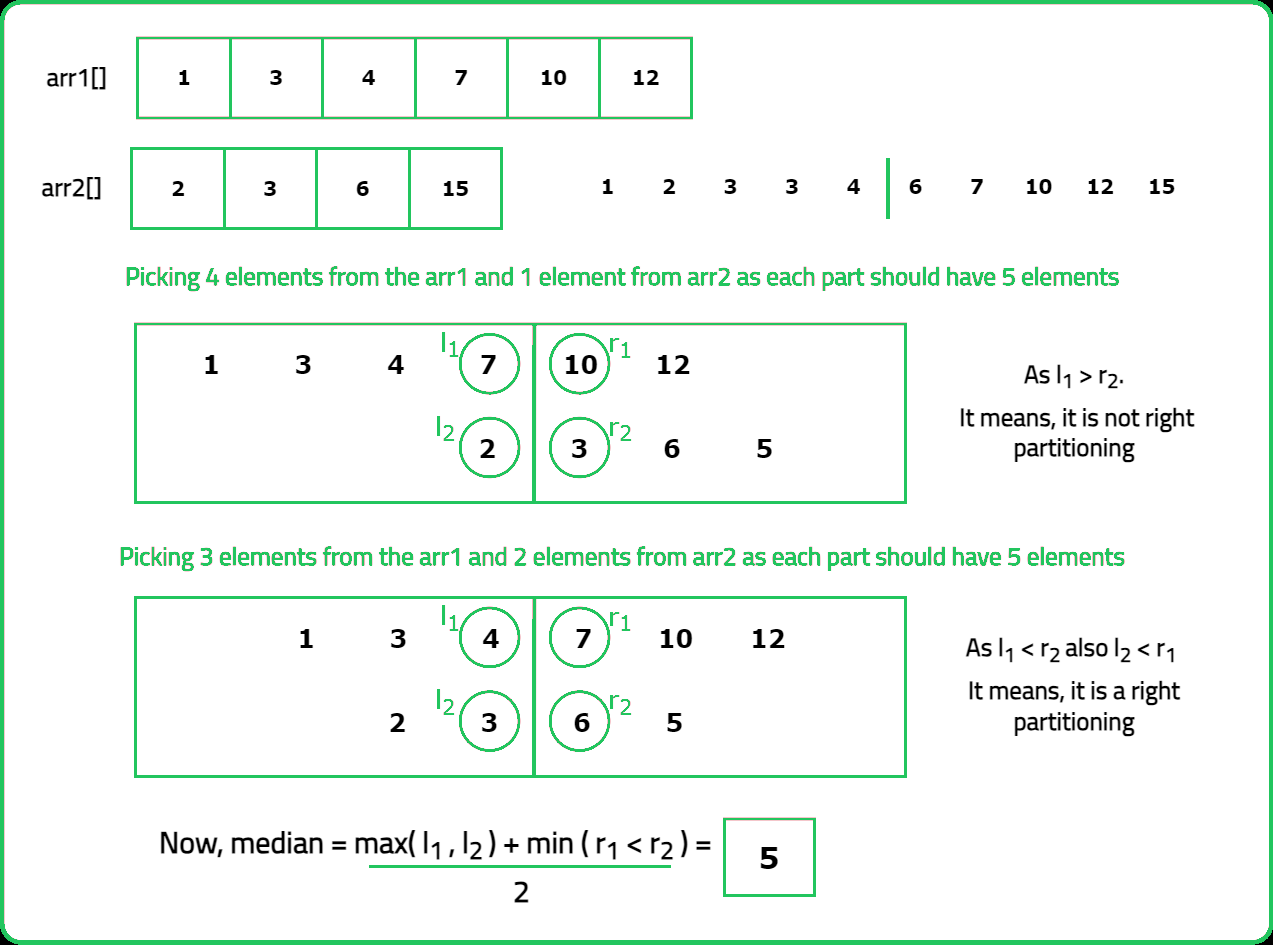
Until now, we have learned how to use binary search but with the assumption that (n1+n2) is even. Let’s generalize this.

If (n1+n2) is odd: In the case of even, we have considered the length of the left half as (n1+n2) / 2. In this case, that length will be (n1 + n2 + 1) / 2. This much change is enough to handle the case of odd. The rest of the things will be completely the same. As in the code, division refers to integer division, this modified formula (n1+n2+1) / 2 will be valid for both cases of odd and even.

What will be the answer i.e. the median:

If l1 <= r2 && l2 <= r1: This condition assures that we have found the correct elements.
If (n1+n2) is odd: The median will be max(l1, l2). Otherwise, median = (max(l1, l2) + min(r1, r2)) / 2.0

Note: We are applying binary search on the possible values of x i.e. [0, n1]. Here n1 is the length of arr1[]. Now, to further optimize it, we will consider the smaller array as arr1[]. So, the actual range will be [0, min(n1, n2)].

Approach:

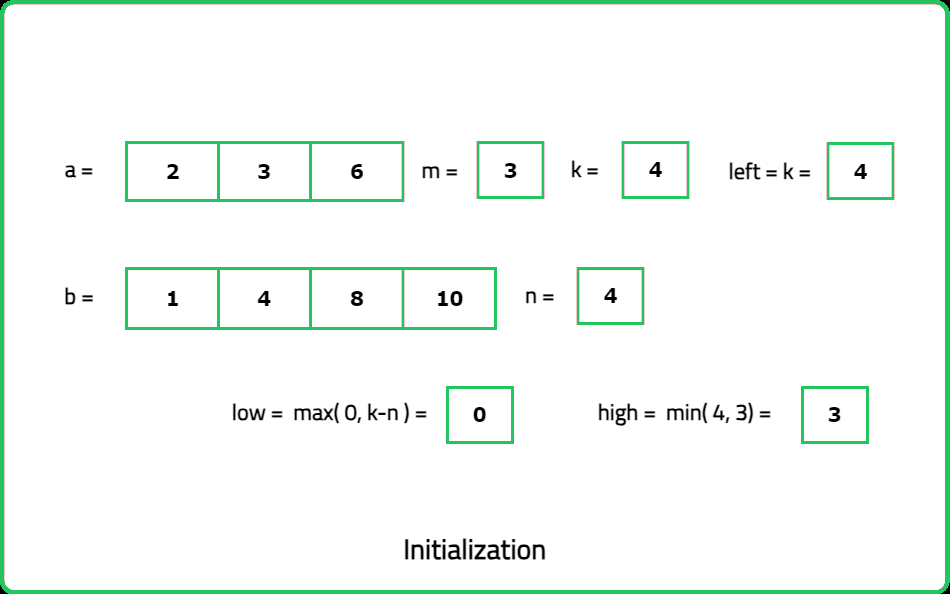
First, make sure that the arr1 is the smaller array. If not by default, just swap the arrays. Our main goal is to consider the smaller array as arr1[]. Calculate the length of the left half as (n1+n2+1) / 2.
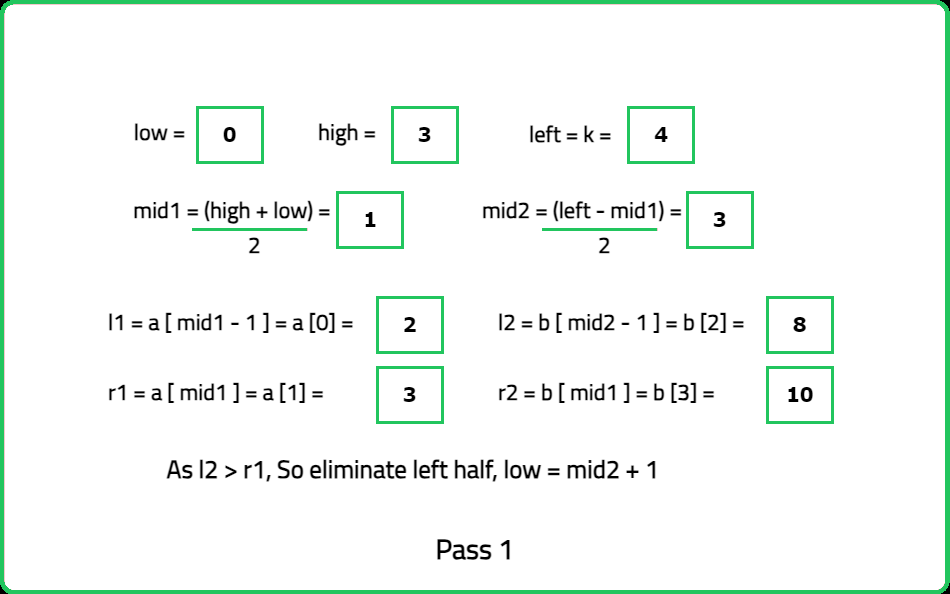
Initialize two pointers: low and high, low will point to 0 and the high will point to n1(i.e. The size of arr1). Calculate the ‘mid1’ i.e. x and ‘mid2’ i.e. [left-x]. Now, inside the loop, calculate the value of ‘mid1’ using the following formula, mid1 = (low+high) // 2 ( ‘//’ refers to integer division) and mid2 = left-mid1.
Calculate l1, l2, r1, and r2: Generally,

l1 = arr1[mid1-1]
l2 = arr2[mid2-1]
r1 = arr1[mid1]
r2 = arr2[mid2]

The possible values of ‘mid1’ and ‘mid2’ might be 0 and n1 and n2 respectively. So, to handle these cases, store some default values for these four variables. The default value for l1 and l2 will be INT_MIN and for r1 and r2, it will be INT_MAX.
Eliminate the halves based on the following conditions:
If l1 is less than or equal to r2 and l2 less than or equal to r1, the answer has been found.
1. If sum of size of the arrays is odd, return the median as maximum of (l1, l2). Otherwise, return median as the average of max(l1, l2)+min(r1, r2).
If l1 is greater than r2. This implies that more elements from arr1 have been considered than needed. So, try to take less elements from arr1 and more from arr2. In such a scenario, take smaller values of x. To achieve this, eliminate the right half (high = mid1-1).
If l2 greater than r1. This implies that we have considered more elements from arr2 than needed. So, try to take less elements from arr2 and more from arr1. In such a scenario, take bigger values of x. To achieve this, eliminate the left half (low = mid1+1).
Finally, outside the loop, include a dummy return statement just to avoid warnings or errors.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find the median of two sorted arrays.
    double median(vector<int>& arr1, vector<int>& arr2) {
        // Size of two given arrays
        int n1 = arr1.size(), n2 = arr2.size();

        /* Ensure arr1 is not larger than 
        arr2 to simplify implementation*/
        if (n1 > n2) return median(arr2, arr1);

        int n = n1 + n2;
        
        // Length of left half
        int left = (n1 + n2 + 1) / 2; 

        // Apply binary search
        int low = 0, high = n1;
        while (low <= high) {
            
            // Calculate mid index for arr1
            int mid1 = (low + high) >> 1; 
            
            // Calculate mid index for arr2
            int mid2 = left - mid1; 

            // Calculate l1, l2, r1, and r2
            int l1 = (mid1 > 0) ? arr1[mid1 - 1] : INT_MIN;
            int r1 = (mid1 < n1) ? arr1[mid1] : INT_MAX;
            int l2 = (mid2 > 0) ? arr2[mid2 - 1] : INT_MIN;
            int r2 = (mid2 < n2) ? arr2[mid2] : INT_MAX;

            if (l1 <= r2 && l2 <= r1) {
                // If condition for finding median
                if (n % 2 == 1) return max(l1, l2);
                else return (max(l1, l2) + min(r1, r2)) / 2.0;
            } 
            else if (l1 > r2) {
                // Eliminate the right half of arr1
                high = mid1 - 1;
            } else {
                // Eliminate the left half of arr1
                low = mid1 + 1;
            }
        }
        // Dummy statement
        return 0; 
    }
};

int main() {
    vector<int> arr1 = {1, 4, 7, 10, 12};
    vector<int> arr2 = {2, 3, 6, 15};

    // Create an instance of the Solution class
    Solution sol;

    // Print the median of the two sorted arrays
    cout << "The median of two sorted arrays is " << fixed << setprecision(1)
         << sol.median(arr1, arr2) << '\n';

    return 0;
}
import java.util.*;

class Solution {
    //Function to find the median of two sorted arrays.
    public double median(int[] arr1, int[] arr2) {
        // Size of two given arrays
        int n1 = arr1.length, n2 = arr2.length;

        /* Ensure arr1 is not larger than 
        arr2 to simplify implementation*/
        if (n1 > n2) return median(arr2, arr1);

        int n = n1 + n2;
        
        // Length of left half
        int left = (n1 + n2 + 1) / 2; 

        // Apply binary search
        int low = 0, high = n1;
        while (low <= high) {
            
            // Calculate mid index for arr1
            int mid1 = (low + high) >>> 1; 
            
            // Calculate mid index for arr2
            int mid2 = left - mid1; 

            // Calculate l1, l2, r1, and r2
            int l1 = (mid1 > 0) ? arr1[mid1 - 1] : Integer.MIN_VALUE;
            int r1 = (mid1 < n1) ? arr1[mid1] : Integer.MAX_VALUE;
            int l2 = (mid2 > 0) ? arr2[mid2 - 1] : Integer.MIN_VALUE;
            int r2 = (mid2 < n2) ? arr2[mid2] : Integer.MAX_VALUE;

            if (l1 <= r2 && l2 <= r1) {
                // If condition for finding median
                if (n % 2 == 1) return Math.max(l1, l2);
                else return (Math.max(l1, l2) + Math.min(r1, r2)) / 2.0;
            } 
            else if (l1 > r2) {
                // Eliminate the right half of arr1
                high = mid1 - 1;
            } else {
                // Eliminate the left half of arr1
                low = mid1 + 1;
            }
        }
        // Dummy statement
        return 0; 
    }

    public static void main(String[] args) {
        int[] arr1 = {1, 4, 7, 10, 12};
        int[] arr2 = {2, 3, 6, 15};

        // Create an instance of the Solution class
        Solution sol = new Solution();

        // Print the median of the two sorted arrays
        System.out.printf("The median of two sorted arrays is %.1f\n", sol.median(arr1, arr2));
    }
}
class Solution:
    #Function to find the median of two sorted arrays.
    def median(self, arr1, arr2):
        # Size of two given arrays
        n1, n2 = len(arr1), len(arr2)

        """ Ensure arr1 is not larger than 
        arr2 to simplify implementation"""
        if n1 > n2:
            return self.median(arr2, arr1)

        n = n1 + n2
        # Length of left half
        left = (n1 + n2 + 1) // 2 

        # Apply binary search
        low, high = 0, n1
        while low <= high:
            # Calculate mid index for arr1
            mid1 = (low + high) // 2 
            
            # Calculate mid index for arr2
            mid2 = left - mid1 

            # Calculate l1, l2, r1, and r2
            l1 = arr1[mid1 - 1] if mid1 > 0 else float('-inf')
            r1 = arr1[mid1] if mid1 < n1 else float('inf')
            l2 = arr2[mid2 - 1] if mid2 > 0 else float('-inf')
            r2 = arr2[mid2] if mid2 < n2 else float('inf')

            if l1 <= r2 and l2 <= r1:
                # If condition for finding median is satisfied
                if n % 2 == 1:
                    return max(l1, l2)
                else:
                    return (max(l1, l2) + min(r1, r2)) / 2.0
            elif l1 > r2:
                # Eliminate the right half of arr1
                high = mid1 - 1
            else:
                # Eliminate the left half of arr1
                low = mid1 + 1
        # Dummy statement
        return 0

if __name__ == "__main__":
    arr1 = [1, 4, 7, 10, 12]
    arr2 = [2, 3, 6, 15]

    # Create an instance of the Solution class
    sol = Solution()

    # Print the median of the two sorted arrays
    print(f"The median of two sorted arrays is {sol.median(arr1, arr2)}")
class Solution {
    //Function to find the median of two sorted arrays.
    median(arr1, arr2) {
        // Size of two given arrays
        const n1 = arr1.length, n2 = arr2.length;

        /* Ensure arr1 is not larger than 
        arr2 to simplify implementation*/
        if (n1 > n2) return this.median(arr2, arr1);

        const n = n1 + n2; // Total length
        // Length of left half
        const left = Math.floor((n1 + n2 + 1) / 2); 

        // Apply binary search
        let low = 0, high = n1;
        while (low <= high) {
            // Calculate mid index for arr1
            const mid1 = Math.floor((low + high) / 2); 
            
            // Calculate mid index for arr2
            const mid2 = left - mid1; 

            // Calculate l1, l2, r1, and r2
            const l1 = (mid1 > 0) ? arr1[mid1 - 1] : -Infinity;
            const r1 = (mid1 < n1) ? arr1[mid1] : Infinity;
            const l2 = (mid2 > 0) ? arr2[mid2 - 1] : -Infinity;
            const r2 = (mid2 < n2) ? arr2[mid2] : Infinity;

            if (l1 <= r2 && l2 <= r1) {
                // If condition for finding median is satisfied
                if (n % 2 === 1) return Math.max(l1, l2);
                else return (Math.max(l1, l2) + Math.min(r1, r2)) / 2.0;
            } else if (l1 > r2) {
                // Eliminate the right half of arr1
                high = mid1 - 1;
            } else {
                // Eliminate the left half of arr1
                low = mid1 + 1;
            }
        }
        // Dummy statement
        return 0; 
    }
}

const arr1 = [1, 4, 7, 10, 12];
const arr2 = [2, 3, 6, 15];

// Create an instance of the Solution class
const sol = new Solution();

// Print the median of the two sorted arrays
console.log(`The median of two sorted arrays is ${sol.median(arr1, arr2)}`);

Complexity Analysis:

Time Complexity: O(log(min(N1,N2))), where N1 and N2 are the sizes of two given arrays. As, binary search is being applied on the range [0, min(N1, N2)]

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code