Shortest Job First
- Fun fact: The Shortest Job First (SJF) or Shortest Job Next (SJN) scheduling policy used in this problem is often utilized by operating systems to manage the execution of processes in real-world applications
- This strategy improves process throughput and utilization of CPU, making it suitable for time-sharing systems where efficiency is critical
- So next time you're working on your PC or using a mobile app, you can imagine a miniature 'queue' of processes, waiting to be handled based on their required computing time!
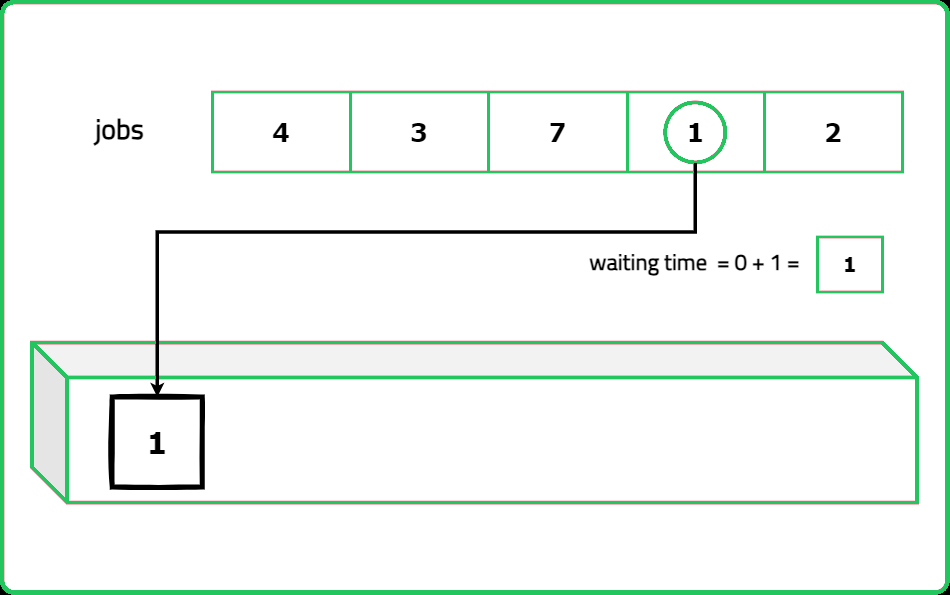
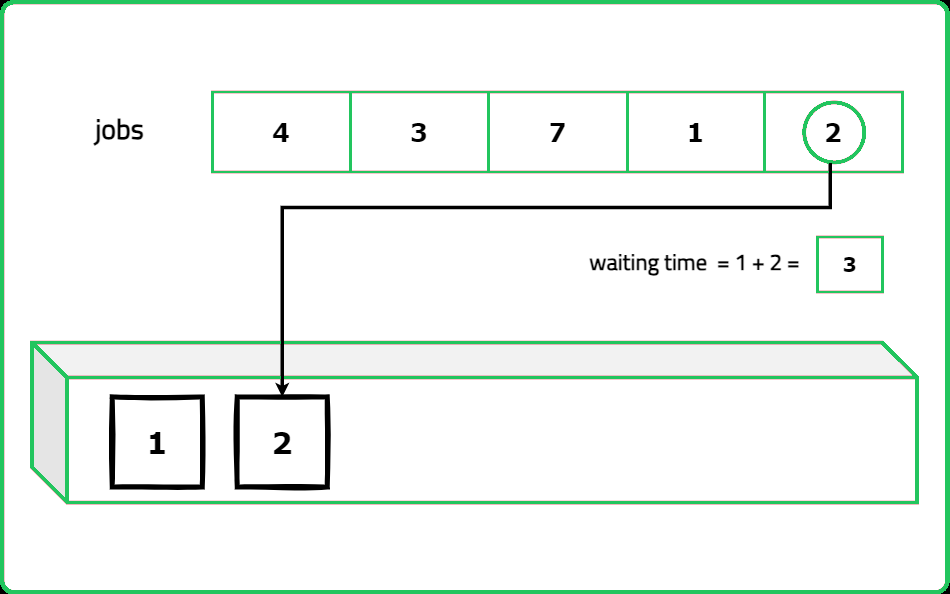
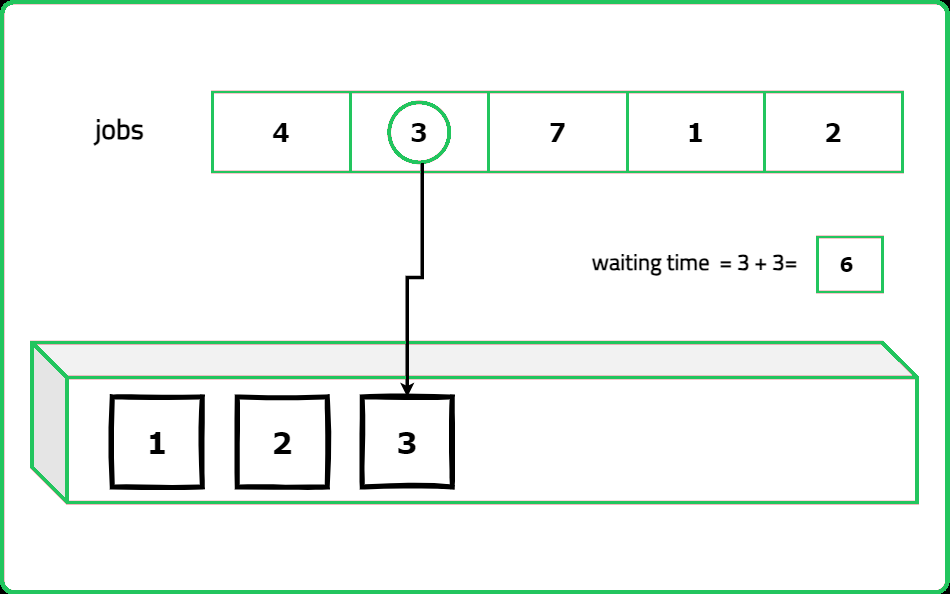
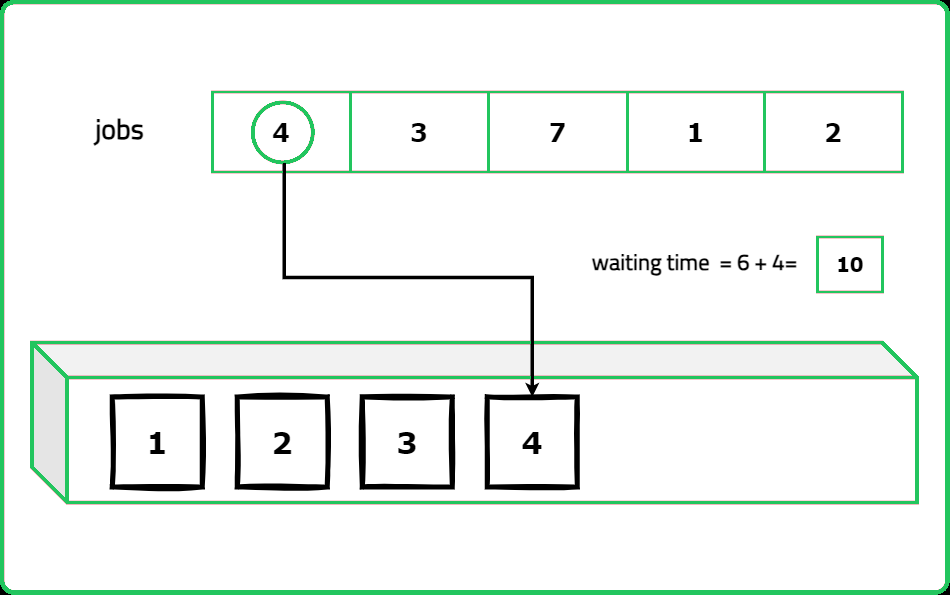
A software engineer is tasked with using the shortest job first (SJF) policy to calculate the average waiting time for each process. The shortest job first also known as shortest job next (SJN) scheduling policy selects the waiting process with the least execution time to run next.
Given an array of n integers representing the burst times of processes, determine the average waiting time for all processes and return the closest whole number that is less than or equal to the result.
Examples:
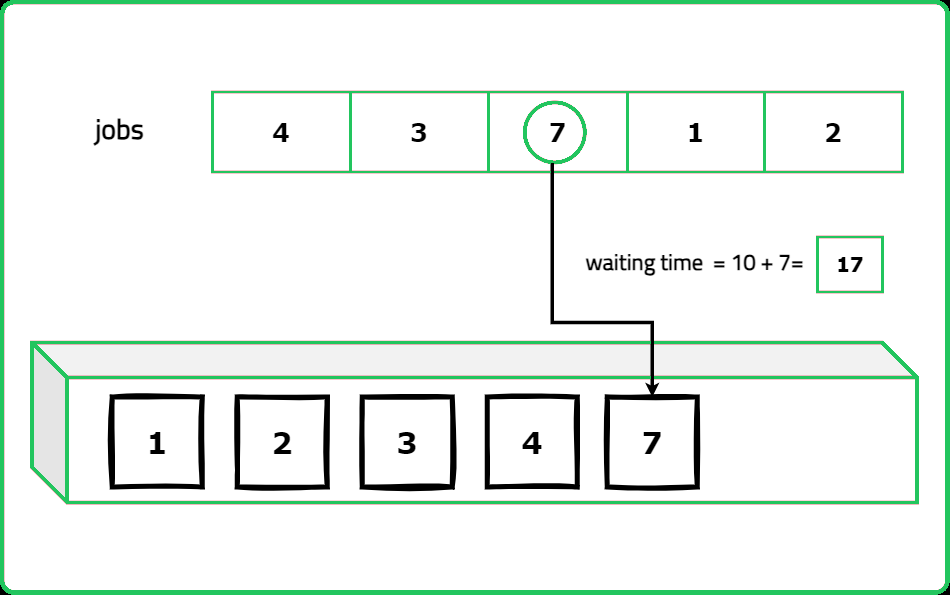
Input : bt = [4, 1, 3, 7, 2]
Output : 4
Explanation : The total waiting time is 20.
So the average waiting time will be 20/5 => 4.
Input : bt = [1, 2, 3, 4]
Output : 2
Explanation : The total waiting time is 10.
So the average waiting time will be 10/4 => 2.
Input : bt = [9, 3, 1, 8, 2]
Constraints
- 1 <= n <= 105
- 1 <= bt[i] <= 105
Hints
- First, sort the burst times in ascending order. For each process, the waiting time is the sum of the burst times of all previous processes.
- "Sum all the waiting times and divide by the total number of processes (n). Use the floor function to return the closest whole number less than or equal to the result. "