Non-overlapping Intervals

Greedy Algorithms Scheduling and Interval Problems Medium

This type of problem scenario and its underlying concept is widely used in the area of resource scheduling in the software industry
For instance, in cloud computing, there can be multiple requests for a resource within overlapping intervals
Solving a problem like this could determine the minimum number of requests to be canceled, moved or rescheduled to ensure that resource allocation does not overlap, thereby optimizing resource utilization
Another popular use case is in the organization of tasks or events in calendar apps where the goal is minimizing event overlap to free up time slots

Given an array of N intervals in the form of (start[i], end[i]), where start[i] is the starting point of the interval and end[i] is the ending point of the interval, return the minimum number of intervals that need to be removed to make the remaining intervals non-overlapping.

Examples:

Input : Intervals = [ [1, 2] , [2, 3] , [3, 4] ,[1, 3] ]

Output : 1

Explanation : You can remove the interval [1, 3] to make the remaining interval non overlapping.

Input : Intervals = [ [1, 3] , [1, 4] , [3, 5] , [3, 4] , [4, 5] ]

Output : 2

Explanation : You can remove the intervals [1, 4] and [3, 5] and the remaining intervals becomes non overlapping.

Input : Intervals = [ [1, 10] , [1, 4] , [3, 8] , [3, 4] , [4, 5] ]

Constraints

1 <= Intervals.length <= 10⁵
0 <= start[i] < end[i] <= 10⁵
Intervals[i].length = 2

Hints

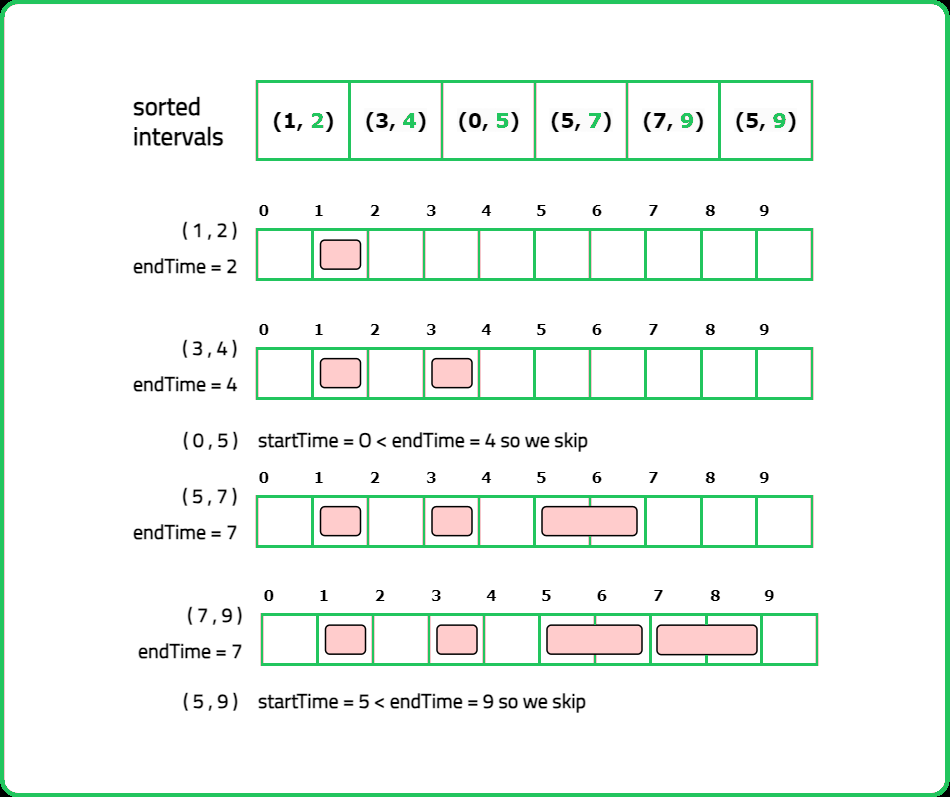
Sort the intervals based on their end values in ascending order. If two intervals have the same end, sort by their start. After sorting, initialize a variable to keep track of the end time of the last selected interval.
Traverse the intervals. If the start time of the current interval is greater than or equal to the end time of the last selected interval, keep the current interval and update the end time. If the intervals overlap (i.e., the start time is less than the current end time), increment the count of intervals to be removed.

Company Tags

Rockstar Games NVIDIA Seagate Technology Docker Goldman Sachs Freshworks Salesforce American Express Red Hat Bungie Morgan Stanley Nutanix Swiggy Texas Instruments Teladoc Health Walmart Zynga Ubisoft Mastercard Bloomberg Stripe Reddit Zomato Deloitte McKinsey & Company Google Microsoft Amazon Meta Apple Netflix Adobe

Intuition

Determining if one interval overlaps with another can be done by checking if the end of the current interval is greater than the start of the next interval. Minimizing the number of intervals to remove involves keeping the end points of the selected intervals as small as possible. This maximizes the space available for subsequent intervals.

Approach

Sort the intervals based on their end times in ascending order to prioritize intervals that finish earliest.
Keep a count of the number of non-overlapping intervals and remember the end time of the last selected interval.
Go through the sorted intervals starting from the second one. For each interval:
- Check if the start time of the current interval is at or after the end time of the last selected interval.
- If it is, select this interval, update the end time to the current interval's end time, and increase the count of non-overlapping intervals.
Determine the minimum number of intervals to remove by subtracting the count of non-overlapping intervals from the total number of intervals.
Return the minimum number of intervals to remove to make the rest non-overlapping.

Dry Run

Solution

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Comparator function to compare intervals based on their ending times
    bool static comp(vector<int>& val1, vector<int>& val2) {
        return val1[1] < val2[1];
    }
    
public:
    // Function to count the maximum number of non-overlapping intervals
    int MaximumNonOverlappingIntervals(vector<vector<int>>& intervals) {
        // Sort the intervals based on their ending times
        sort(intervals.begin(), intervals.end(), comp);
        
        // Get total number of intervals
        int n = intervals.size();
        
        // Initialize counter
        int cnt = 1;
        
        // Keep track of the ending time
        int lastEndTime = intervals[0][1];
        
        // Iterate through all intervals
        for (int i = 1; i < n; i++) {
            /* Check if the starting time of the current 
            interval is greater than or equal to 
            the ending time of the last 
            selected interval */
            if (intervals[i][0] >= lastEndTime) {
                // Increment counter
                cnt++;
                // Update the ending time
                lastEndTime = intervals[i][1];
            }
        }
        return n - cnt;
    }

};

// Main function
int main() {
    vector<vector<int>> intervals = {{0, 5}, {3, 4}, {1, 2}, {5, 9}, {7, 9}};
    
    // Creating an object of solution class
    Solution solution;
    
    // Function call to get the maximum non-overlapping intervals
    int ans = solution.MaximumNonOverlappingIntervals(intervals);
    
    cout << "Maximum Non-Overlapping Intervals: " << ans << endl;
    
    return 0;
}
import java.util.*;

class Solution {
    // Comparator function to compare intervals based on their ending times
    public static int comp(int[] val1, int[] val2) {
        // Compare the ending times of the intervals
        return Integer.compare(val1[1], val2[1]);
    }
    
    // Function to count the maximum number of non-overlapping intervals
    public int MaximumNonOverlappingIntervals(int[][] intervals) {
        // Sort the intervals based on their ending times
        Arrays.sort(intervals, Solution::comp);
    
        // Get total number of intervals
        int n = intervals.length;
    
        // Initialize counter
        int cnt = 1;
    
        // Keep track of the ending time
        int lastEndTime = intervals[0][1];
    
        // Iterate through all intervals
        for (int i = 1; i < n; i++) {
            /* Check if the starting time of the current 
            interval is greater than or equal to 
            the ending time of the last 
            selected interval */
            if (intervals[i][0] >= lastEndTime) {
                // Increment counter
                cnt++;
                // Update the ending time
                lastEndTime = intervals[i][1];
            }
        }
        return n-cnt;
    }
}

// Main class
class Main {
    public static void main(String[] args) {
        Solution obj = new Solution();
        int[][] intervals = {{0, 5}, {3, 4}, {1, 2}, {5, 9}, {7, 9}};
        
        for (int i = 0; i < intervals.length; i++) {
            System.out.println("Interval " + (i + 1) + " Start: " + intervals[i][0] + " End: " + intervals[i][1]);
        }
        
        int ans = obj.MaximumNonOverlappingIntervals(intervals);
        System.out.println("Maximum Non-Overlapping Intervals: " + ans);
    }
}
class Solution:
    # Function to compare intervals based on ending times
    @staticmethod
    def comp(val1, val2):
        # Compare the ending times of the intervals
        return val1[1] < val2[1]

    # Function to count the maximum number of non-overlapping intervals
    def MaximumNonOverlappingIntervals(self, intervals):
        # Sort the intervals based on their ending times
        intervals.sort(key=lambda x: x[1])

        # Get total number of intervals
        n = len(intervals)

        # Initialize counter
        cnt = 1

        # Keep track of the ending time
        last_end_time = intervals[0][1]

        # Iterate through all intervals
        for i in range(1, n):
            # Check if the starting time of the current 
            # interval is greater than or equal to the 
            # ending time of the last selected interval
            if intervals[i][0] >= last_end_time:
                # Increment counter
                cnt += 1
                # Update the ending time
                last_end_time = intervals[i][1]

        return n-cnt

# Example usage
if __name__ == "__main__":
    obj = Solution()
    intervals = [[0, 5], [3, 4], [1, 2], [5, 9], [7, 9]]
    
    for i, interval in enumerate(intervals):
        print(f"Interval {i + 1} Start: {interval[0]} End: {interval[1]}")
    
    ans = obj.MaximumNonOverlappingIntervals(intervals)
    print(f"Maximum Non-Overlapping Intervals: {ans}")
class Solution {
    // Comparator function to compare intervals based on their ending times
    static comp(a, b) {
        // Compare the ending times of the intervals
        return a[1] - b[1];
    }

    // Function to count the maximum number of non-overlapping intervals
    MaximumNonOverlappingIntervals(intervals) {
        // Sort the intervals based on their ending times
        intervals.sort(Solution.comp);

        // Get total number of intervals
        const n = intervals.length;

        // Initialize counter
        let cnt = 1;

        // Keep track of the ending time
        let lastEndTime = intervals[0][1];

        // Iterate through all intervals
        for (let i = 1; i < n; i++) {
            /* Check if the starting time of 
            the current interval is greater
            than or equal to the ending time of
             the last selected interval */
            if (intervals[i][0] >= lastEndTime) {
                // Increment counter
                cnt++;
                // Update the ending time
                lastEndTime = intervals[i][1];
            }
        }
        return n-cnt;
    }
}

// Example usage
const obj = new Solution();
const intervals = [[0, 5], [3, 4], [1, 2], [5, 9], [7, 9]];

intervals.forEach((interval, i) => {
    console.log(`Interval ${i + 1} Start: ${interval[0]} End: ${interval[1]}`);
});

const ans = obj.MaximumNonOverlappingIntervals(intervals);
console.log(`Maximum Non-Overlapping Intervals: ${ans}`);

Complexity Analysis

Time Complexity: O(N log N + N) where N is the number of intervals. We sort the intervals based on their end timings which takes up O(N log N). We then iterate over the sorted intervals to find the maximum number of non-overlapping intervals. Space Complexity: O(1) as no additional data structure has been used.

Code

Problem List