Pow(x,n)
Recursion
Implementation Problems
Easy
- In Google's search algorithm, the concept of power function comes into play
- This algorithm named PageRank, uses power iteration methodology to calculate the ranks of pages
- The basic idea is to count the number and quality of links to a page to determine a rough estimate of how important the page is
- The underlying assumption is that more important pages are likely to receive more links from other websites
- Thus, a mathematically defined multiple number of iterations (x raised to n) helps in providing more precise page rankings
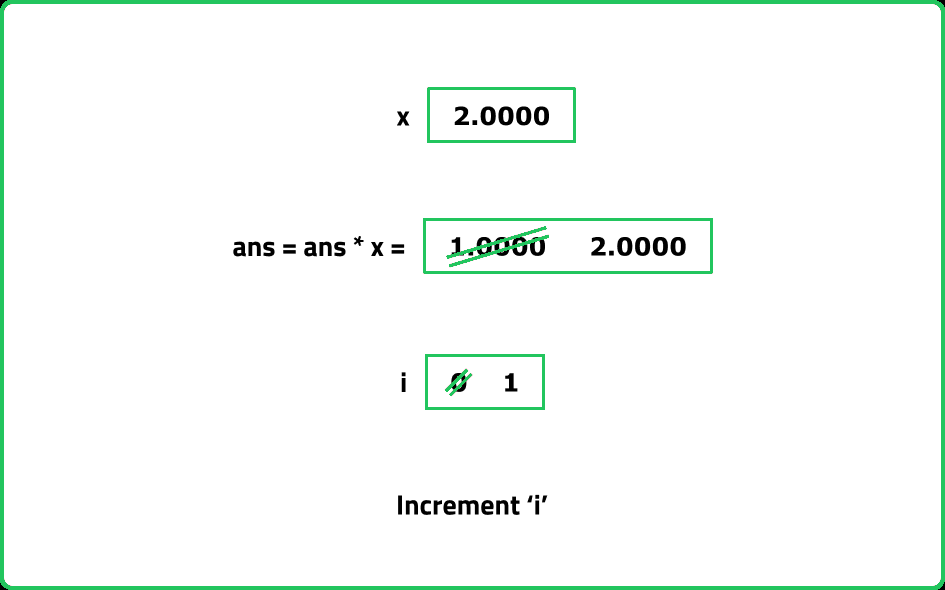
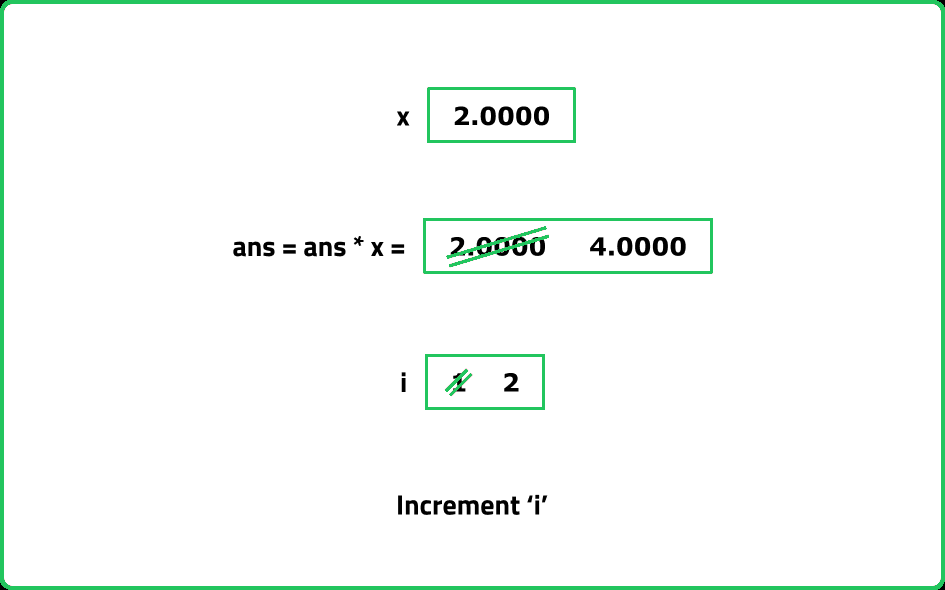
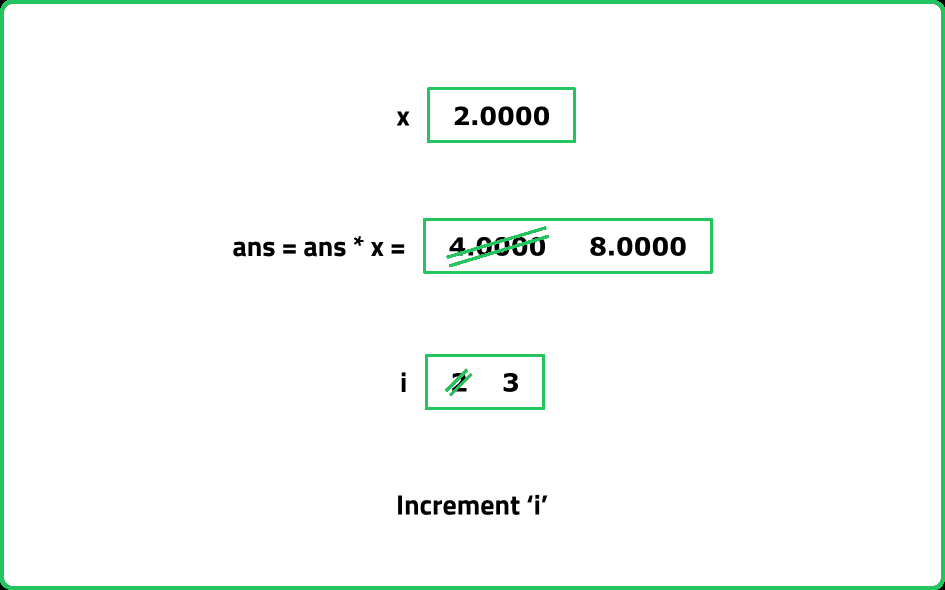
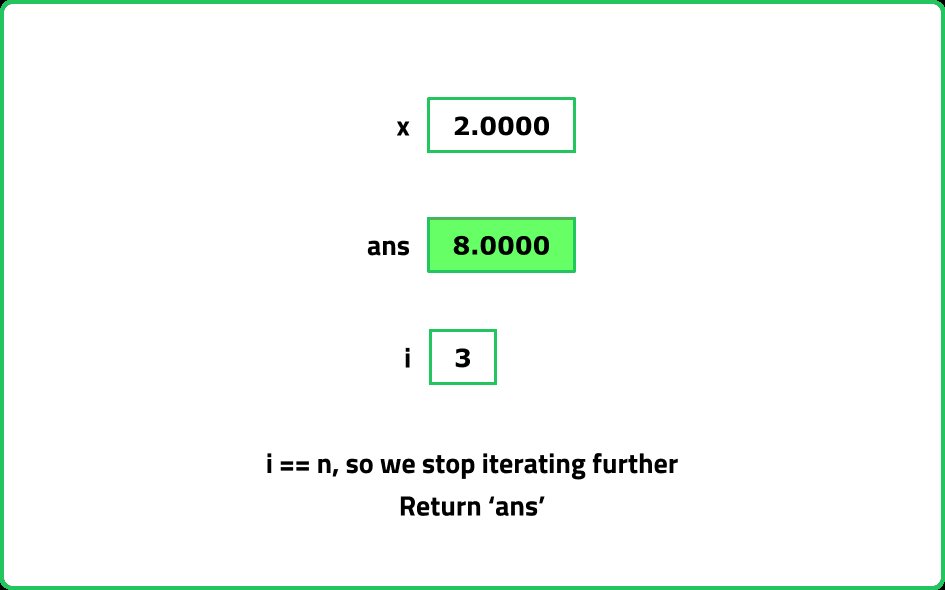
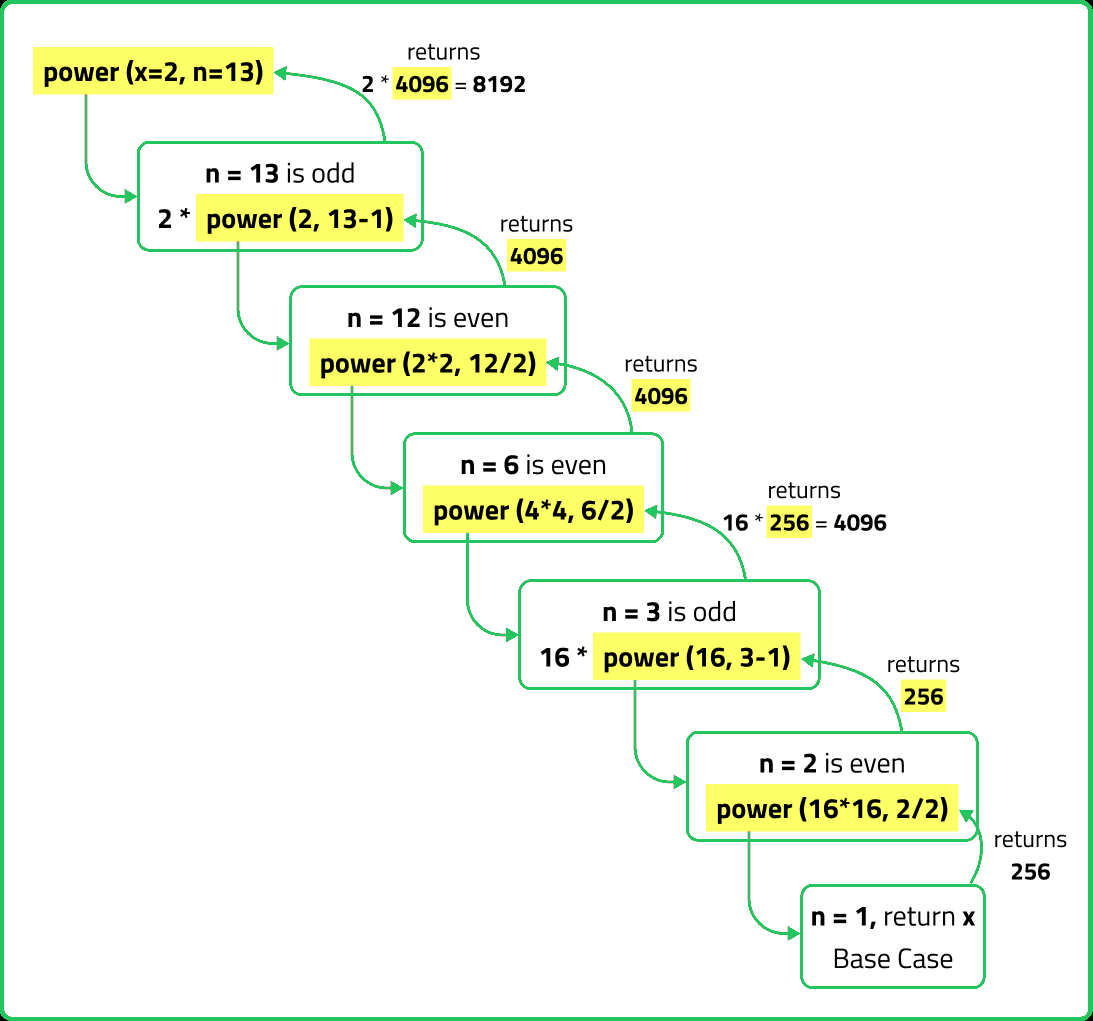
Implement the power function pow(x, n) , which calculates the x raised to n i.e. xn.
Examples:
Input : x = 2.0000 , n = 10
Output : 1024.0000
Explanation : Answer = 2^10 => 1024.
Input : x = 2.0000 , n = -2
Output : 0.2500
Explanation : Answer = 2^(-2) = 1/4 => 0.25.
Input : x = 2.5000 , n = 2
Constraints
- -100.0 <= x <= 100.0
- -231 <= n <= 231 - 1
- -104 <= xn <= 104
- Either x is not zero or n>0.
- n is an integer.
Hints
- Use Exponentiation by Squaring, which reduces the time complexity to O(logn)
- "Iterative: Avoids stack overflow and is more memory-efficient (O(1) space). Recursive: Cleaner and simpler code, but uses O(logn) space due to recursion."
Company Tags
Shopify
Siemens Healthineers
PwC
Ubisoft
Bloomberg
Zynga
Cloudflare
Deloitte
GE Healthcare
Philips Healthcare
Goldman Sachs
Robinhood
Zomato
Roche
Medtronic
Chewy
Western Digital
Cerner
Salesforce
Etsy
Databricks
Square
DoorDash
Morgan Stanley
Splunk
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro