123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
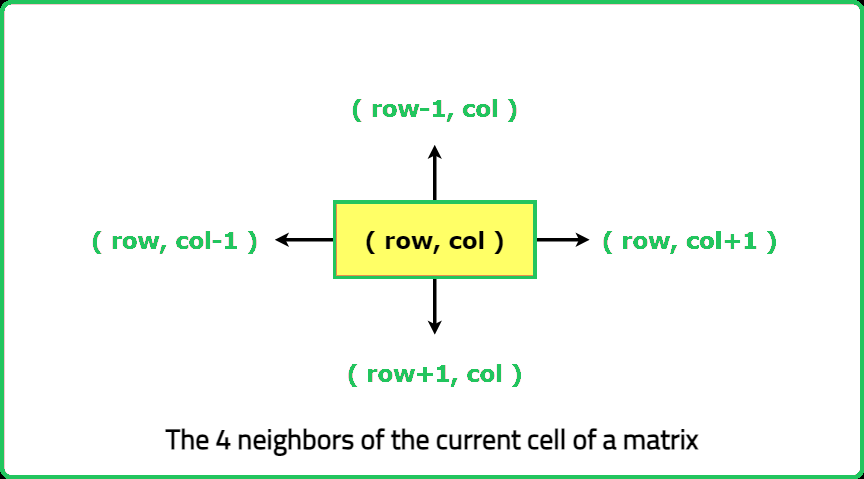
// DelRow and delCol for neighbors
vector<int> delRow = {-1, 0, 1, 0};
vector<int> delCol = {0, 1, 0, -1};
/* Helper Function to check if a
pixel is within boundaries */
bool isValid(int &i, int &j,
int &n, int &m) {
// Return false if pixel is invalid
if(i < 0 || i >= n) return false;
if(j < 0 || j >= m) return false;
// Return true if pixel is valid
return true;
}
// Function to perform DFS traversal
void dfs(int row, int col, vector<vector<int>>&ans,
vector<vector<int>>& image, int newColor,
int iniColor) {
// color with new color
ans[row][col] = newColor;
// Getting the dimensions of image
int n = image.size();
int m = image[0].size();
// Traverse the 4 neighbors
for(int i=0; i < 4; i++) {
// Coordinates of new pixel
int nrow = row + delRow[i];
int ncol = col + delCol[i];
/* check for valid, unvisited pixels
having same initial color */
if(isValid(nrow, ncol, n, m) &&
image[nrow][ncol] == iniColor
&& ans[nrow][ncol] != newColor) {
// Recirsively perform DFS
dfs(nrow, ncol, ans, image,
newColor, iniColor);
}
}
}
public:
// Function to perform flood fill algorithm
vector<vector<int>> floodFill(vector<vector<int>> &image,
int sr, int sc, int newColor) {
// Store initial color
int iniColor = image[sr][sc];
// To store the updated image
vector<vector<int>> ans = image;
// Start DFS traversal from start cell
dfs(sr, sc, ans, image, newColor, iniColor);
// Return the answer image
return ans;
}
};
int main() {
vector<vector<int>> image = {
{1,1,1},
{1,1,0},
{1,0,1}
};
int sr = 1, sc = 1;
int newColor = 2;
int n = image.size();
int m = image[0].size();
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to find the
number of islands in given grid*/
vector<vector<int>> ans = sol.floodFill(image, sr, sc, newColor);
cout << "Image after performing flood fill algorithm: \n\n";
for(int i=0; i < n; i++) {
for(int j=0; j < m; j++) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697
import java.util.*;
class Solution {
// DelRow and delCol for neighbors
private int[] delRow = {-1, 0, 1, 0};
private int[] delCol = {0, 1, 0, -1};
/* Helper Function to check if a
pixel is within boundaries */
private boolean isValid(int i, int j,
int n, int m) {
// Return false if pixel is invalid
if (i < 0 || i >= n) return false;
if (j < 0 || j >= m) return false;
// Return true if pixel is valid
return true;
}
// Function to perform DFS traversal
private void dfs(int row, int col, int[][] ans,
int[][] image, int newColor,
int iniColor) {
// color with new color
ans[row][col] = newColor;
// Getting the dimensions of image
int n = image.length;
int m = image[0].length;
// Traverse the 4 neighbors
for (int i = 0; i < 4; i++) {
// Coordinates of new pixel
int nrow = row + delRow[i];
int ncol = col + delCol[i];
// check for valid, unvisited pixels
// having same initial color
if (isValid(nrow, ncol, n, m) &&
image[nrow][ncol] == iniColor &&
ans[nrow][ncol] != newColor) {
// Recursively perform DFS
dfs(nrow, ncol, ans, image,
newColor, iniColor);
}
}
}
public int[][] floodFill(int[][] image, int sr,
int sc, int newColor) {
// Store initial color
int iniColor = image[sr][sc];
// To store the updated image
int[][] ans = new int[image.length][image[0].length];
for (int i = 0; i < image.length; i++) {
ans[i] = Arrays.copyOf(image[i], image[i].length);
}
// Start DFS traversal from start cell
dfs(sr, sc, ans, image, newColor, iniColor);
// Return the answer image
return ans;
}
public static void main(String[] args) {
int[][] image = {
{1, 1, 1},
{1, 1, 0},
{1, 0, 1}
};
int sr = 1, sc = 1;
int newColor = 2;
// Creating an instance of Solution class
Solution sol = new Solution();
// Function call to find the number of islands in given grid
int[][] ans = sol.floodFill(image, sr, sc, newColor);
System.out.println("Image after performing flood fill algorithm:\n");
for (int[] row : ans) {
for (int col : row) {
System.out.print(col + " ");
}
System.out.println();
}
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
class Solution:
def __init__(self):
# delRow and delCol for neighbors
self.delRow = [-1, 0, 1, 0]
self.delCol = [0, 1, 0, -1]
def isValid(self, i, j, n, m):
# Return false if pixel is invalid
if i < 0 or i >= n:
return False
if j < 0 or j >= m:
return False
# Return true if pixel is valid
return True
def dfs(self, row, col, ans, image, newColor, iniColor):
# color with new color
ans[row][col] = newColor
# Getting the dimensions of image
n = len(image)
m = len(image[0])
# Traverse the 4 neighbors
for i in range(4):
# Coordinates of new pixel
nrow = row + self.delRow[i]
ncol = col + self.delCol[i]
# check for valid, unvisited pixels
# having same initial color
if (
self.isValid(nrow, ncol, n, m) and
image[nrow][ncol] == iniColor and
ans[nrow][ncol] != newColor
):
# Recursively perform DFS
self.dfs(nrow, ncol, ans, image, newColor, iniColor)
def floodFill(self, image, sr, sc, newColor):
# Store initial color
iniColor = image[sr][sc]
# To store the updated image
ans = [row[:] for row in image]
# Start DFS traversal from start cell
self.dfs(sr, sc, ans, image, newColor, iniColor)
# Return the answer image
return ans
# Testing the function
image = [
[1, 1, 1],
[1, 1, 0],
[1, 0, 1]
]
sr, sc = 1, 1
newColor = 2
sol = Solution()
ans = sol.floodFill(image, sr, sc, newColor)
print("Image after performing flood fill algorithm:\n")
for row in ans:
print(" ".join(map(str, row)))
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
class Solution {
constructor() {
// delRow and delCol for neighbors
this.delRow = [-1, 0, 1, 0];
this.delCol = [0, 1, 0, -1];
}
isValid(i, j, n, m) {
// Return false if pixel is invalid
if (i < 0 || i >= n) return false;
if (j < 0 || j >= m) return false;
// Return true if pixel is valid
return true;
}
dfs(row, col, ans, image, newColor, iniColor) {
// color with new color
ans[row][col] = newColor;
// Getting the dimensions of image
const n = image.length;
const m = image[0].length;
// Traverse the 4 neighbors
for (let i = 0; i < 4; i++) {
// Coordinates of new pixel
const nrow = row + this.delRow[i];
const ncol = col + this.delCol[i];
// check for valid, unvisited pixels
// having same initial color
if (this.isValid(nrow, ncol, n, m)
&& image[nrow][ncol] == iniColor
&& ans[nrow][ncol] != newColor ) {
// Recursively perform DFS
this.dfs(nrow, ncol, ans, image, newColor, iniColor);
}
}
}
floodFill(image, sr, sc, newColor) {
// Store initial color
const iniColor = image[sr][sc];
// To store the updated image
const ans = image.map(row => row.slice());
// Start DFS traversal from start cell
this.dfs(sr, sc, ans, image, newColor, iniColor);
// Return the answer image
return ans;
}
}
// Testing the function
const image = [
[1, 1, 1],
[1, 1, 0],
[1, 0, 1]
];
const sr = 1, sc = 1;
const newColor = 2;
const sol = new Solution();
const ans = sol.floodFill(image, sr, sc, newColor);
console.log("Image after performing flood fill algorithm:\n");
ans.forEach(row => {
console.log(row.join(" "));
});