Count primes in range L to R

Maths Sieve of Eratosthenes Hard

You are given an 2D array queries of dimension n*2.

The queries[i] represents a range from queries[i][0] to queries[i][1] (include the end points).

Return the count of prime numbers present in between each range in queries array.

Examples:

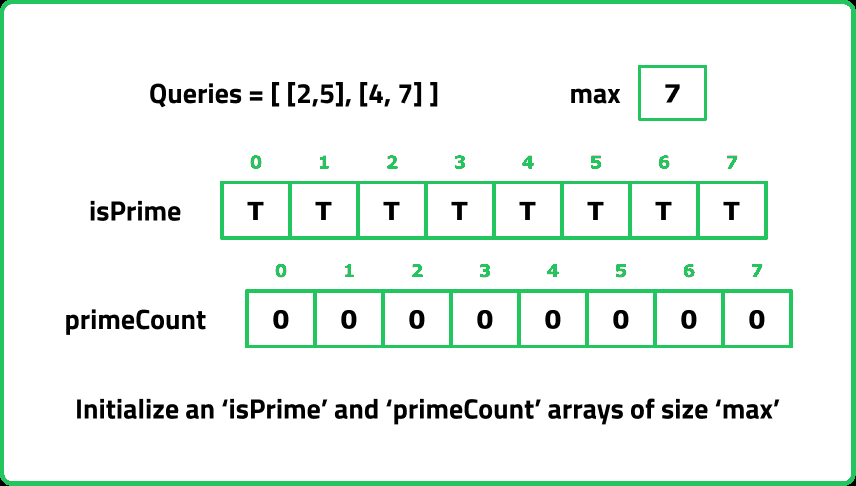
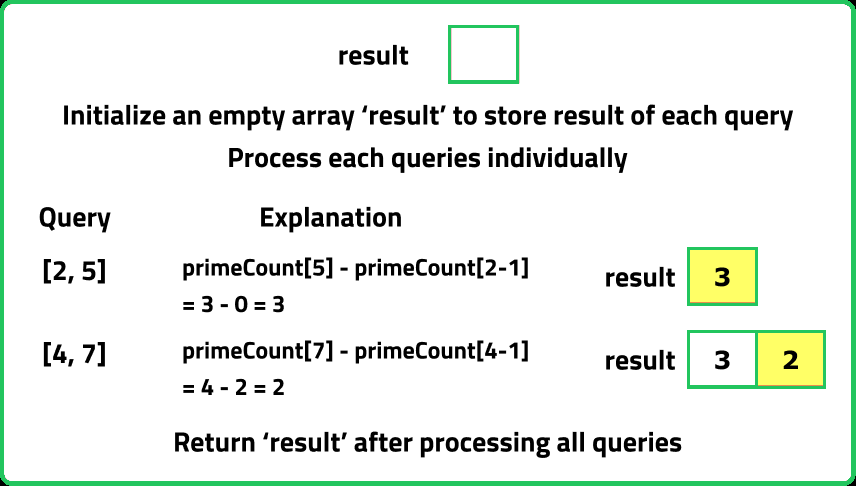
Input : queries = [ [2, 5], [4, 7] ]

Output : [3, 2]

Explanation : The range 2 to 5 contains three prime numbers 2, 3, 5.

The range 4 to 7 contains two prime numbers 5, 7.

Input : queries = [ [1, 7], [3, 7] ]

Output : [4, 3]

Explanation : The range 1 to 7 contains four prime numbers 2, 3, 5, 7.

The range 3 to 7 contains three prime numbers 3, 5, 7.

Input : queries = [ [1, 10], [10, 20] ]

Constraints

1 <= n <= 10⁵
1 <= queries[i][0] <= queries[i][1] <= 10⁵

Hints

A brute-force approach would check each number in the range [L, R] for primality using trial division, resulting in O(n√m) complexity (where m is the largest number in queries). This is inefficient for large R.
"A better approach is the Prefix Sum of Primes using the Sieve of Eratosthenes: Precompute all primes up to max(R) using the Sieve of Eratosthenes (O(m log log m)). Build a prefix sum array where prime_count[i] stores the count of primes from 1 to i (O(m))."

Company Tags

Reddit Zomato Salesforce Zynga Target American Express Lyft Docker Walmart Unity Technologies eBay Mastercard JPMorgan Chase Bain & Company Twilio Byju's Optum Freshworks Siemens Healthineers PwC Broadcom Ubisoft Robinhood Texas Instruments Wayfair Google Microsoft Amazon Meta Apple Netflix Adobe

Intuition

The problem involves determining the number of prime numbers within a given range [L, R] for multiple queries. Given that the number of queries (Q) can be quite large (up to 100,000) and the range can extend up to 1,000,000, a straightforward approach would not be efficient. Initially, the thought process involves recognizing that for each query, checking each number in the range [L, R] to see if it is prime would be computationally expensive. Therefore, an optimized strategy is necessary. A prime checking mechanism that avoids redundant calculations for each query is crucial to handle large inputs efficiently.

Approach

The following approach, based on the provided code snippet, outlines an effective solution:

Define a function that accepts a list of queries, where each query is a pair of integers (L, R).

Determine the number of queries (Q) from the size of the list.

Iterate through each query extract L and R from the current query and Initialize a count variable to zero for tracking the number of primes in the current range. For each number j in the range [L, R], check if it is a prime number:

If j is prime, increment the count.

After processing the range, output the count of prime numbers for the current query.

Solution

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    vector<int> primesInRange(vector<pair<int, int>>& queries) {
       // Vector to store the results of each query
        vector<int> result; 

        for (auto& query : queries) {
            int l = query.first; // Starting point of the range
            int r = query.second; // Ending point of the range
            int count = 0; // Counter for the number of prime numbers

            for (int j = l; j <= r; j++) {
            // Check if the number is prime  
                if (isPrime(j)) 
                    count++;
            }
            // Store the result for the current query
            result.push_back(count); 
        }

        return result;
    }

private:
    bool isPrime(int n) {
        if (n <= 1) return false;
        for (int i = 2; i <= sqrt(n); i++) {
            if (n % i == 0) return false;
        }
        return true;
    }
};

// Main method for testing
int main() {
    Solution solution;
    vector<pair<int, int>> queries = {{3, 10}, {8, 20}, {1, 5}};
    vector<int> result = solution.primesInRange(queries);

    for (int count : result) {
        cout << count << endl; // Print the result for each query
    }

    return 0;
}
import java.util.ArrayList;

class Solution {
    public ArrayList<Integer> primesInRange(ArrayList<int[]> queries) {
        // List to store the results of each query
        ArrayList<Integer> result = new ArrayList<>(); 

        for (int[] query : queries) {
            int l = query[0]; // Starting point of the range
            int r = query[1]; // Ending point of the range
            int count = 0; // Counter for the number of prime numbers

            for (int j = l; j <= r; j++) {
            // Check if the number is prime
                if (isPrime(j)) 
                    count++;
            }
           // Store the result for the current query
            result.add(count); 
        }

        return result;
    }

    private boolean isPrime(int n) {
        if (n <= 1) return false;
        for (int i = 2; i <= Math.sqrt(n); i++) {
            if (n % i == 0) return false;
        }
        return true;
    }

    // Main method for testing
    public static void main(String[] args) {
        Solution solution = new Solution();
        ArrayList<int[]> queries = new ArrayList<>();
        queries.add(new int[]{3, 10});
        queries.add(new int[]{8, 20});
        queries.add(new int[]{1, 5});
        ArrayList<Integer> result = solution.primesInRange(queries);

        for (int count : result) {
            System.out.println(count); // Print the result for each query
        }
    }
}
class Solution:
    def primesInRange(self, queries):
        # List to store the results of each query
        result = [] 

        for l, r in queries:
            # Counter for the number of prime numbers
            count = 0 

            for j in range(l, r + 1):
                # Check if the number is prime
                if self.isPrime(j): 
                    count += 1
                    # Store the result for the current query
            result.append(count) 

        return result

    def isPrime(self, n):
        if n <= 1:
            return False
        for i in range(2, int(n ** 0.5) + 1):
            if n % i == 0:
                return False
        return True

# Main method for testing
if __name__ == "__main__":
    solution = Solution()
    queries = [(3, 10), (8, 20), (1, 5)]
    result = solution.primesInRange(queries)

    for count in result:
        print(count) 
class Solution {
    primesInRange(queries) {
        // Array to store the results of each query
        let result = []; 

        for (let [l, r] of queries) {
            // Counter for the number of prime numbers
            let count = 0; 

            for (let j = l; j <= r; j++) {
                // Check if the number is prime
                if (this.isPrime(j)) 
                    count++;
            }
            // Store the result for the current query
            result.push(count); 
        }

        return result;
    }

    isPrime(n) {
        if (n <= 1) return false;
        for (let i = 2; i <= Math.sqrt(n); i++) {
            if (n % i === 0) return false;
        }
        return true;
    }
}

// Main method for testing
const solution = new Solution();
const queries = [[3, 10], [8, 20], [1, 5]];
const result = solution.primesInRange(queries);

for (const count of result) {
    console.log(count); 
}

Complexity Analysis

Time Complexity The naive approach described above checks each number in the range [L, R] for primality in each query. The primality check itself has a complexity of O(√n), where n is the number being checked. Thus, for each query, the time complexity is O((R-L+1)√R). Given Q queries, the overall time complexity becomes O(Q * (R-L+1) * √R). This is inefficient for large values of Q and R.

Space Complexity:O(1) since it uses a constant amount of additional space regardless of the input size.

Intuition

The problem requires counting prime numbers within specified ranges for multiple queries efficiently. A direct approach of checking each number within the range for primality would be computationally expensive, especially for large ranges. Instead, precomputing the prime numbers up to the maximum value in the queries using the Sieve of Eratosthenes, followed by utilizing a prefix sum array to store the cumulative count of primes up to each index, provides a more efficient solution. This allows for quick retrieval of the count of primes within any given range by leveraging the prefix sum array.

Approach

Identify the maximum value present in all the queries to determine the upper limit for prime number computation.
Use the Sieve of Eratosthenes to precompute all prime numbers up to the identified maximum value.
Create a prefix sum array where each index stores the cumulative count of prime numbers from the start up to that index.
For each query, utilize the prefix sum array to quickly determine the count of prime numbers within the specified range. This is achieved by subtracting the prefix sum value at the start of the range from the value at the end of the range.
Return the results for all queries as a list of counts of prime numbers within the respective ranges.

Dry Run

Solution

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    std::vector<int> primesInRange(std::vector<std::vector<int>>& queries) {
        if (queries.empty()) {
            return {};
        }

        // Find the maximum value in the queries 
        // to determine the sieve range
        int maxVal = 0;
        for (const auto& query : queries) {
            maxVal = std::max(maxVal, query[1]);
        }

        // Step 1: Use the Sieve of Eratosthenes 
        // to find all primes up to maxVal
        std::vector<bool> isPrime(maxVal + 1, true);
        isPrime[0] = isPrime[1] = false;  // 0 and 1 are not primes
        for (int p = 2; p * p <= maxVal; ++p) {
            if (isPrime[p]) {
                for (int i = p * p; i <= maxVal; i += p) {
                    isPrime[i] = false;
                }
            }
        }

        // Step 2: Create a prefix sum array 
        // to count primes up to each number
        std::vector<int> primeCount(maxVal + 1, 0);
        for (int i = 1; i <= maxVal; ++i) {
            primeCount[i] = primeCount[i - 1];
            if (isPrime[i]) {
                primeCount[i]++;
            }
        }

        // Step 3: Process each query to find the number of primes 
        // in the given range
        std::vector<int> result;
        for (const auto& query : queries) {
            int start = query[0];
            int end = query[1];
            if (start == 0) {
                result.push_back(primeCount[end]);
            } else {
                result.push_back(primeCount[end] - primeCount[start - 1]);
            }
        }

        return result;
    }
};

// Example usage
std::vector<std::vector<int>> queries = {{2, 5}, {4, 7}};
Solution solution;
auto result = solution.primesInRange(queries); // Output: [3, 2]
import java.util.ArrayList;
import java.util.List;

class Solution {
    public ArrayList<Integer> primesInRange(ArrayList<int[]> queries) {
        if (queries == null || queries.isEmpty()) {
            return new ArrayList<>();
        }

        // Find the maximum value in the queries 
        // to determine the sieve range
        int maxVal = 0;
        for (int[] query : queries) {
            maxVal = Math.max(maxVal, query[1]);
        }

        // Step 1: Use the Sieve of Eratosthenes 
        // to find all primes up to maxVal
        boolean[] isPrime = new boolean[maxVal + 1];
        for (int i = 2; i <= maxVal; i++) {
            isPrime[i] = true;
        }
        for (int p = 2; p * p <= maxVal; p++) {
            if (isPrime[p]) {
                for (int i = p * p; i <= maxVal; i += p) {
                    isPrime[i] = false;
                }
            }
        }

        // Step 2: Create a prefix sum array 
        // to count primes up to each number
        int[] primeCount = new int[maxVal + 1];
        for (int i = 1; i <= maxVal; i++) {
            primeCount[i] = primeCount[i - 1];
            if (isPrime[i]) {
                primeCount[i]++;
            }
        }

        // Step 3: Process each query to find the number 
        // of primes in the given range
        ArrayList<Integer> result = new ArrayList<>();
        for (int[] query : queries) {
            int start = query[0];
            int end = query[1];
            if (start == 0) {
                result.add(primeCount[end]);
            } else {
                result.add(primeCount[end] - primeCount[start - 1]);
            }
        }

        return result;
    }
}

// Example usage:
ArrayList<int[]> queries = new ArrayList<>();
queries.add(new int[]{2, 5});
queries.add(new int[]{4, 7});
Solution solution = new Solution();
System.out.println(solution.primesInRange(queries)); // Output: [3, 2]
class Solution:
    def primesInRange(self, queries):
        if not queries:
            return []

        # Find the maximum value in the queries 
        # to determine the sieve range
        max_val = max(max(q) for q in queries)
        
        # Step 1: Use the Sieve of Eratosthenes 
        # to find all primes up to max_val
        is_prime = [True] * (max_val + 1)
        # 0 and 1 are not primes
        is_prime[0] = is_prime[1] = False  
        
        p = 2
        while p * p <= max_val:
            if is_prime[p]:
                for i in range(p * p, max_val + 1, p):
                    is_prime[i] = False
            p += 1
        
        # Step 2: Create a prefix sum array 
        # to count primes up to each number
        prime_count = [0] * (max_val + 1)
        for i in range(1, max_val + 1):
            prime_count[i] = prime_count[i - 1]
            if is_prime[i]:
                prime_count[i] += 1
        
        # Step 3: Process each query to find the 
        # number of primes in the given range
        result = []
        for q in queries:
            start, end = q
            if start == 0:
                result.append(prime_count[end])
            else:
                result.append(prime_count[end] - prime_count[start - 1])
        
        return result

# Example usage:
queries = [[2, 5], [4, 7]]
solution = Solution()
print(solution.primesInRange(queries))  # Output: [3, 2]

queries = [[1, 7], [3, 7]]
print(solution.primesInRange(queries))  # Output: [4, 3]
class Solution {
    primesInRange(queries) {
        if (!queries || queries.length === 0) {
            return [];
        }

        // Find the maximum value in the queries 
        // to determine the sieve range
        let maxVal = 0;
        for (let query of queries) {
            maxVal = Math.max(maxVal, query[1]);
        }

        // Step 1: Use the Sieve of Eratosthenes 
        // to find all primes up to maxVal
        let isPrime = Array(maxVal + 1).fill(true);
        // 0 and 1 are not primes
        isPrime[0] = isPrime[1] = false;  

        for (let p = 2; p * p <= maxVal; p++) {
            if (isPrime[p]) {
                for (let i = p * p; i <= maxVal; i += p) {
                    isPrime[i] = false;
                }
            }
        }

        // Step 2: Create a prefix sum array 
        // to count primes up to each number
        let primeCount = Array(maxVal + 1).fill(0);
        for (let i = 1; i <= maxVal; i++) {
            primeCount[i] = primeCount[i - 1];
            if (isPrime[i]) {
                primeCount[i]++;
            }
        }

        // Step 3: Process each query to find 
        // the number of primes in the given range
        let result = [];
        for (let query of queries) {
            let [start, end] = query;
            if (start === 0) {
                result.push(primeCount[end]);
            } else {
                result.push(primeCount[end] - primeCount[start - 1]);
            }
        }

        return result;
    }
}

// Example usage:
let queries = [[2, 5], [4, 7]];
let solution = new Solution();
console.log(solution.primesInRange(queries));  // Output: [3, 2]

queries = [[1, 7], [3, 7]];
console.log(solution.primesInRange(queries));  // Output: [4, 3]

Complexity Analysis

Time Complexity: O(N log (log N)) for the Sieve of Eratosthenes, where n is the maximum value in the queries. The prefix sum computation takes O(n), and each query is processed in O(1) time. Thus, the overall time complexity is dominated by the sieve, resulting inO(N log (log N)).

Space Complexity: O(N) for storing the prime status array and the prefix sum array, where n is the maximum value in the queries. The space complexity is primarily due to the storage of these arrays, with each requiring space proportional to the maximum value.

Code

Problem List

Count primes in range L to R

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition

Approach

Solution

Complexity Analysis

Intuition

Approach

Dry Run

Solution

Complexity Analysis

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code